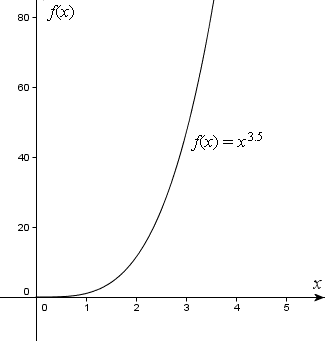Trong toán học, ta thường gặp một ký hiệu toán học $n!$
Ký hiệu $n!$ được gọi là “$n$ giai thừa”, là tích của
$$n!=n\left( n-1 \right)\left( n-2 \right)\ldots 2.1$$
Giai thừa thường được sử dụng trong các bài toán đếm và xác suất, ví dụ như hoán vị (đếm sự sắp xếp và chú ý đến thứ tự của các đối tượng) và tổ hợp (không quan trọng sự thay đổi thứ tự của các đối tượng), cả hai dạng bài toán trên sử dụng giai thừa khi dữ liệu về các đối tượng trong bài toán có số lượng khá lớn.
Cũng tương tự vậy, việc tìm xác suất để chiến thắng trong các trò chơi xổ số hay chơi bài cũng đòi hỏi sử dụng giai thừa.
Ví dụ về giai thừa:
$$2!=2\times 1=2$$
$$3!=3\times 2\times 1=6$$
$$4!=4\times 3\times 2\times 1=24$$
$$5!=5\times 4\times 3\times 2\times 1=120$$
Ngoài cách biểu diễn trên, chúng ta có thể viết giai thừa dưới dạng “ký hiệu tích” (thường gọi là “pi”) như sau:
$$n!=\underset{k=1}{\overset{n}{\mathop \prod }}\,k$$
Còn ký hiệu $\mathop{\sum }^{}$ gọi là “ký hiệu tổng”. Nhưng trong trường hợp này chúng ta “nhân” chứ không “cộng”.
Ví dụ: Với $n=4$, chúng ta sẽ thay thế $k=1$, $k=2$, $k=3$ và $k=4$ và viết lại như sau:
$$4!=\underset{k=1}{\overset{4}{\mathop \prod }}\,4\times 3\times 2\times 1=24$$
$0!$ là một trường hợp đặc biệt. Có nhiều trường hợp mà $0!$ có ý nghĩa và $0!$ có giá trị là$~1$ chứ không phải là $0$. Do vậy, theo quy ước, ta có:
$$0!=1$$
Ngoài ra, $1!$ cũng có giá trị là $1$:
$$1!=1$$
Đồ thị $f\left( n \right)=n!$, với $n\in N$ được biểu diễn như sau:
Các điểm $A\left( 0,1 \right)$, $B\left( 1;1 \right)$, $C\left( 2;2 \right)$, $D\left( 3;6 \right)$, $E\left( 4;24 \right)$ là các điểm rời rạc trong không gian, ta không thể nối các điểm đó thành một đường cong. Với lại, giai thừa không có nghĩa nếu như $~n$ không là số tự nhiên. Ví dụ như không có giá trị của: $3,5!$ (3,5 giai thừa).
Tuy nhiên, đồ thị của chúng ta gợi nên một đường cong có các giá trị tăng nhanh chóng, giống như hàm số mũ.
Vậy câu hỏi được đặt ra là: Chúng ta có thể tìm được một đồ thị hàm số chứa các điểm biểu diễn giai thừa hay không? Hóa ra là có!
I. HÀM GAMMA
Hàm Gamma là một khái niệm mở rộng của giai thừa. Chúng ta có thể xác định (gần như) bất kỳ số thực hay số phức bằng hàm Gamma và tìm giá trị của chúng. Và các giá trị này có liên quan đến các giá trị giai thừa.
Có một trường hợp đặc biệt mà chúng ta có thể thấy sự liên quan, tính kết nối giữa các con số giai thừa.
Với $n$ là một số nguyên dương, hàm Gamma (đặt tên theo chữ cái Hy Lạp có ký hiệu là $''\mathbf{\Gamma }''$ bởi nhà toán học Legendre) của $n$ là:
$$\text{ }\!\!\Gamma\!\!\text{ }\left( n \right)=\left( n-1 \right)!$$
Và chúng ta có thể chuyển thành dạng $n!$ như sau:
$$\text{ }\!\!\Gamma\!\!\text{ }\left( n+1 \right)=n!$$
Tuy nhiên, một điều đặc biệt là hàm Gamma không bị giới hạn bởi các số nguyên. Và một công thức khác, cho phép ta tìm giá trị của hàm Gamma với một số thực $n$ bất kỳ như sau:
$$\text{ }\!\!\Gamma\!\!\text{ }\left( n+1 \right)=\underset{0}{\overset{\infty }{\mathop \int }}\,{{e}^{-x}}.{{x}^{n}}dx$$
Ví dụ: Với $n=3.5$. Chúng ta muốn tìm giá trị của $3.5!$, giả sử giá trị này tồn tại.
Giá trị của $\text{ }\!\!\Gamma\!\!\text{ }\left( 3.5+1 \right)=\text{ }\!\!\Gamma\!\!\text{ }\left( 4.5 \right)$ tính bởi tích phân vô hạn:
$$\text{ }\!\!\Gamma\!\!\text{ }\left( 4.5 \right)=\underset{0}{\overset{\infty }{\mathop \int }}\,{{e}^{-x}}.{{x}^{3.5}}dx$$
Kiểm tra đồ thị ở trên, chúng ta hi vọng rằng giá trị của $3.5!$ nằm trong khoảng $10$ đến $15$ (Chúng ta đã kiểm tra được $3!=6$ và $4!=24$. Do đó mà $3.5!$ có giá trị nằm trong khoảng này.)
II. Ý NGHĨA DẤU TÍCH PHÂN?
Có một sự thú vị với hàm $f\left( x \right)={{e}^{-x}}.{{x}^{3.5}}$. Đây là tích của một hàm giảm với một hàm tăng.
Chúng ta cùng quan sát đồ thị của các hàm số này.
Đầu tiên, $f\left( x \right)={{e}^{-x}}$. Ta thấy giá trị của $f\left( x \right)$ (chiều cao của đồ thị) sẽ giảm khi $x$ tăng
Tiếp đó, $f\left( x \right)={{x}^{3.5}}$ tăng khi $x$ tăng.
Tập xác định của hàm này là các số thực không âm.
Cuối cùng, chúng ta sẽ quan sát đồ thị của tích hai hàm này:
$$f\left( x \right)={{e}^{-x}}.{{x}^{3.5}}$$
Diện tích miền tô đậm của đồ thị trên từ $0$ đến $\infty $ (vô cùng) cho ta giá trị của $\text{ }\!\!\Gamma\!\!\text{ }\left( 4.5 \right)=3.5!$
Chúng ta sử dụng phần mềm toán học trên máy tính để tìm giá trị của tích phân. Chúng ta chỉ cần chọn một số dương bất kỳ đủ lớn (Ở đây ta chọn số $10000$) cho giới hạn trên của tích phân, như các bạn có thể thấy trong biểu đồ, chiều cao của đường cao là rất nhỏ khi $x$ tăng lên một giá trị rất lớn. Dưới đây là những gì chúng ta nhận được:
$$\text{ }\!\!\Gamma\!\!\text{ }\left( 4,5 \right)=\underset{0}{\overset{10000}{\mathop \int }}\,{{e}^{-x}}.{{x}^{3.5}}\approx 11,6317$$
Điều này có nghĩa là diện tích phần tô màu ở đồ thị trên có giá trị là $11.6317$ (đơn vị diện tích) . Con số này nằm trong khoảng chúng ta đã ước tính ở trên.
III. TRỞ LẠI ĐỒ THỊ
Chúng ta trở lại đồ thị, quan sát giá trị của các giai thừa. Bằng việc sử dụng tích phân như trên ta tính được giá trị của hàm Gamma với mọi số thực $n$.
Đồ thị này là một đường cong đi qua các điểm biểu diễn giá trị giai thừa. Hàm số của đồ thị này là: $f\left( n \right)=\text{ }\!\!\Gamma\!\!\text{ }\left( n+1 \right)$
Qua đó, ta thêm điểm $F\left( 3.5;11.6317 \right)$, điểm này đại diện cho $\text{ }\!\!\Gamma\!\!\text{ }\left( 4,5 \right)=11.6317$. Và ta thấy, đường cong của đồ thị chứa điểm $F$ đi qua các giá trị giai thừa khác.
Ta có thể xem thêm thông tin của $\text{ }\!\!\Gamma\!\!\text{ }\left( 4,5 \right)$ tại
http://www.wolframal...t/?i=gamma(4.5)
IV. KẾT LUẬN
Hàm Gamma cho chúng ta giá trị giai thừa của các số thực. Đây là một đóng góp to lớn của nhà toán học Leonhard Euler, người Thụy Sĩ cho nền toán học Thế Giới.
Trước khi kết thúc vấn đề này, chúng ta cùng nhìn vào đồ thị $f\left( n \right)=\text{ }\!\!\Gamma\!\!\text{ }\left( n+1 \right)$ trong một phạm vi lớn hơn. Chúng ta thấy rằng, hàm số này không liên tục với $n$ nguyên âm.
Nguồn: http://www.intmath.c...a-function-4350
Người dịch: Phan Thành Nhân - Thành viên Chuyên san EXP
Bài viết đã được chỉnh sửa nội dung bởi hoangtrong2305: 11-11-2015 - 21:08