Chủ đề này có 49 trả lời

[hxthanh]

Theo điều lệ, các đội chuẩn bị đề và đáp án nộp cho hxthanh, hạn cuối cùng là ngày 12/02/2012

Bài viết đã được chỉnh sửa nội dung bởi PSW: 11-04-2012 - 15:59

[hxthanh]

Đề thi của GAMMA:
Download ở đây: http://www.mediafire...ryvr4vhhdwwc24n
Hoặc ở đây:  De thach dau Gama goi Beta - tran II.pdf   110.61K   370 Số lần tải


ĐỀ THI CỦA ĐỘI BETA

Bài 1 (THCS):
Giải hệ phương trình
\[\left\{ \begin{array}{l}
\sum {\frac{{2{y^2} + xy + yz + zx}}{{(x - y)(z - y)}} = 2\sum {\frac{1}{{xy}}} } \\
3\left( {x + \frac{1}{x}} \right) = 4\left( {y + \frac{1}{y}} \right) = 6\left( {z + \frac{1}{z}} \right)
\end{array} \right.\]
Trong đó $\sum f(a,b,c)=f(a,b,c)+f(b,c,a)+f(c,a,b)$.

Bai 2 (THCS): Cho tam giác ABC có BC là cạnh nhỏ nhất. Lấy E trên AC và D trên AB sao cho $BC=BD=CE$. Chứng minh bán kính đường tròn ngoại tiếp $\triangle ADE$ bằng khoảng cách giữa tâm đường tròn ngoại tiếp và tâm đường tròn nội tiếp của $\triangle ABC$


Bài 3 (THPT):
Giải hệ phương trình:
$\left\{ \begin{array}{l}
{\rm{y}}\sin x = {\log _2}\left| {\frac{{{\rm{y}}\sin x}}{{1 + 3y}}} \right|(1)\\
\left( {6{y^2} + 2y} \right)\left( {{4^{{{\sin }^2}x}} + {4^{c{\rm{o}}{{\rm{s}}^2}x}}} \right)=25y^2+6y+1(2)\\
\left| y \right| \le 1(3)
\end{array} \right.$

Bài 4(THPT):
Tính giá trị biểu thức:
$\cos\frac{\pi}{50}.\cos\frac{19\pi}{50}.\cos\frac{31\pi}{50}.\cos\frac{39\pi}{50}+\cos\frac{\pi}{50}.\cos\frac{2\pi}{50}.\cos\frac{19\pi}{50}.\cos\frac{39\pi}{50}+2\cos\frac{\pi}{10}$


Bài 5 (THPT):
Tứ giác ABCD là tứ giác không nội tiếp, các đường trung trực của AB, AD cắt nhau tại A’, các đường trung trực của AB,BC cắt nhau tại B’, các đường trung trực của BC, CD cắt nhau tại C’, các đường trung trực của AD, DC cắt nhau tại D’. CMR: ABCD ngoại tiếp được một đường tròn khi và chỉ khi A’B’C’D’ ngoại tiếp được một đường tròn.


Bài 6 (Olympic):
Từ một tam giác nhọn ${T_0}$ người ta dựng một dãy vô hạn những tam giác ${T_0},{T_1},{T_2}...$ theo qua tắc sau: Các đỉnh của tam giác ${T_{i + 1}}$ là các tiếp điểm của các cạnh tam giác ${T_i}$ với đường tròn nội tiếp của tam giác đó $\left( {i = 0,1,2...} \right)$. Gọi ${p_i}$ là nửa chu vi tam giác ${T_i}$. Chứng minh rằng $\forall n\left( {n = 1,2,...} \right)$ ta có
${p_0} > \sum\limits_{i = 1}^n {{p_i}} $
Tam giác ${T_0}$ cần có điều kiện gì để ta có:
${p_0} = \mathop {\lim }\limits_{n \to + \infty } \left( {\sum\limits_{i = 1}^n {{p_i}} } \right)$

[Trần Đức Anh @@]

Trần Đức Anh @@ của đội BETA giải bài 1 của GAMA:
Nhân phương trình thứ hai với -8 rồi cộng với phương trình thứ nhất, ta được
$(x-2)^4=(y-4)^4$
$\Leftrightarrow x-2=y-4$ $\vee$ $x-2=4-y$
$\Leftrightarrow x=y-2$ $\vee$ $x=6-y$
Thay vào phương trình đầu ta được:
$(1):$ $-8y^3+24y^2-32y+16=240$ $\Leftrightarrow $ $(y+2)(y^2-5y+14)$. Suy ra $y=-2$ và $x=-4$
$(2):$ $-24y^3+216y^2-864y+1296=240$
$\Leftrightarrow $ $(y-2)(y^2-7y+22)=0$. Suy ra $y=2$ và $x=4$.
Vậy hệ đã cho có 2 nghiệm là $(x,y)$ $= (-4, -2)$ và $(x, y)$ $= (4, 2)$.

________________________________________________________________
@Trọng tài: Lời giải đúng, nhưng quá vắn tắt, chú ý trình bày (Trừ $1$ điểm)!

Điểm: 5/6

Bài viết đã được chỉnh sửa nội dung bởi hxthanh: 22-06-2012 - 22:03

[khanh3570883]

Không biết có đúng hay không, mình nghĩ câu Olimpic của Gama hình như sai đề vì khi thay a = 2, b = 1, c = 2 thì $\varphi \left( {{b^a} + {c^a}} \right) = 5$ còn 2a = 4. Rõ ràng 4 không là ước của 5

[perfectstrong]

Không biết có đúng hay không, mình nghĩ câu Olimpic của Gama hình như sai đề vì khi thay a = 2, b = 1, c = 2 thì $\varphi \left( {{b^a} + {c^a}} \right) = 5$ còn 2a = 4. Rõ ràng 4 không là ước của 5

Trong trường hợp của anh thì $\varphi(b^a+c^a)=\varphi(5)=4$ vì 5 là số nguyên tố. Dĩ nhiên $2a|4$. Đề không sai.

[Trần Đức Anh @@]

Trần Đức Anh @@ của đội BETA giả bài 4 của GAMA
Xét bổ đề: Nếu $XYZT$ là hình thang vuông $(X=T=90^0)$ thì đường trung trực của $XT$ đi qua trung điểm của $YZ$.
Chứng minh: Từ $Y$ kẻ $YH\bot TZ$ ta có: đường trung trực của $XT$ cắt $YH$ tại trung điểm của $YH$, áp dụng định lý về đường trung bình của tam giác cho tam giác $YHZ$ ta được đpcm.
Trở lại bài toán:
Gọi $A$, $B$ thuộc $(I)$ và $C$, $D$ thuộc $(O)$ theo thứ tự nằm trên đoạn thẳng chắn theo đề ra.
Gọi $P$, $Q$, $S$ lần lượt là trung điểm của $AB$, $BC$, $CD$. Sử dụng bổ đề ta có $IP\bot AD$, $OS\bot AD$ suy ra $IP\bot OS$, mà $Q$ là trung điểm của $SP$ suy ra đường vuông hóc với $SP$ sẽ đi qua trung điểm $M$ của $OI$. TA có: $MI=\frac{1}{2}OI=6$(cm).
Tương tự: đường trung trực của $PQ$ đi qua $B$ và trung điểm $T$ của $MI$, $TI=3$(cm) suy ra $T$ thuộc $(I)$ suy ra $\widehat{TBA}=90^0$ và $O$, $I$, $A$ thẳng hàng.
Đặt $AP=PB=BQ=QC=CS=SD=x$ và $IP=\frac{1}{5}OS=y$ thì theo định lý Pythagore ta có hệ:
$\left\{\begin{matrix}x^2+y^2=3^2\\x^2+9^2=(5y)^2\end{matrix}\right.$
$\Leftrightarrow$ $\left\{\begin{matrix}x=\sqrt{6}\\y=\sqrt{3}\end{matrix}\right.$
Vậy mỗi đoạn chắn bằng $2\sqrt{6}$(cm).

__________________________________________________________
@ Trọng tài: Lời giải hay, phù hợp THCS ()
Tuy nhiên, không có hình vẽ (Trừ $1$ điểm)
Lập hệ phương trình sai!
Hệ đúng phải là $\begin{cases}x^2+y^2=3^2 \\ x^2+(5y)^2=9^2\end{cases}$
Vậy mà đáp số lại đúng! ??? (Trừ $1$ điểm)
Lưu ý! Đáp án đề nghị của GAMMA sai ! (Cộng cho BETA 1 điểm )

Điểm: 6/7

Bài viết đã được chỉnh sửa nội dung bởi hxthanh: 22-06-2012 - 21:48

[Ispectorgadget]

Câu a mình chưa làm ra ai bên Beta làm ra thì post lên cho hoàn thiện câu này
Ispectorgadget đội Beta xin giải Bài 2 câu b của Gama

Giả sử tồn tại 1 đường tròn có 2012 điểm nguyên. Gọi đường tròn tâm $O$. Xét một phần tư đường tròn, do tính đối xứng và chỉ có đúng 2012 điểm nguyên nên chọn được 4 điểm nguyên $A,B,C,D$ đối xứng nhau và $AC$ vuông góc $BD$ qua tâm $O$ (1)
Thấy cả đường tròn chỉ có đúng 2012 điểm
do vậy $\dfrac{1}{4}$ đường tròn chỉ có đúng 503 điểm, là số lẻ
Gọi một phần tư đường tròn đó là $AOB$ thì góc $AOB=90^o$ gọi $OK$ phân giác góc $AOB$ do đó $OK$ chia góc này thành 2 góc $45^o$
Vì $503$ lẻ nên sẽ có một điểm nguyên rơi vào $OK$ do nếu không có điểm nguyên nào rơi vào $OK$ thì theo tính đối xứng thấy nếu có điểm $L$ nguyên thuộc cung $KB$ thì sẽ tồn tại một điểm nguyên $L'$ khác thuộc cung $KA$ nguyên do đó số điểm trên $AOB$ phải chẵn mâu thuẫn!!!
Do vậy phải có 1 điểm rơi vào $OK$ giả sử là $K' \rightarrow K'=K$
Ta thấy điểm $A$ nguyên (do (1)) do đó $OA$ nguyên,
Hạ $KH$ vuông góc $OB$ khi đó tam giác $KOH$ vuông cân tại $H$ do đó $KH=\sqrt{2}.OK=\sqrt{2}.OA$
Do vậy $KH$ không nguyên
Mà $OA,OB$ đều bằng nhau và nguyên nên $O$ là điểm nguyên (vì Nếu $O$ không nguyên thì hoặc $A$ hoặc $B$ không nguyên vô lý) do đó khoảng cách từ O đến x nguyên gọi đó là $p$ do đó khoảng cách từ $K \to x$ là $KH+ p$ mà $KH$ không nguyên nên $KH+p$ không nguyên do đó $K$ không nguyên nên ko có đường tròn thỏa đề!!
__________________________________________________
@ Trọng tài: Rất tiếc lập luận của em sai lầm hoàn toàn. Đường tròn chứa các điểm nguyên đâu bắt buộc có tâm là điểm nguyên???
Đáp án đúng: Tồn tại!

Điểm 0/6

Bài viết đã được chỉnh sửa nội dung bởi hxthanh: 23-06-2012 - 16:33

[Ispectorgadget]

Mong đội Gama gõ đề lên cho mọi người tiện theo dõi.

[perfectstrong]

Perfectstrong đội Gama xin giải quyết bài 2 đội Beta
Lời giải 1:

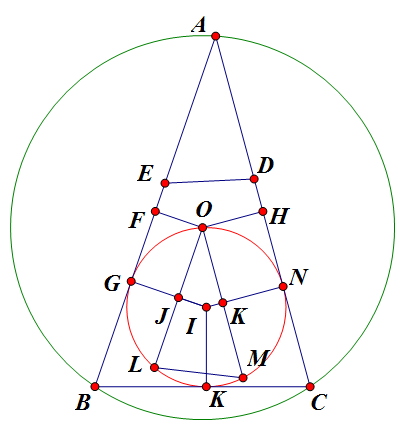
Không mất tính tổng quát, giả sử $BC \leq CA \leq AB$ (do BC là cạnh nhỏ nhất trong 3 cạnh $\vartriangle ABC$)
Gọi I,O thứ tự là tâm đường tròn nội tiếp, ngoại tiếp $\vartriangle ABC$.
Vẽ F,G lần lượt là hình chiếu của O,I lên AB; H,N thứ tự là hình chiếu của O,I lên AC.
Gọi L,M là điểm đối xứng của O qua IG,IN tương ứng. OL, OM cắt IG,IN tương ứng tại J,K.
Do đó, IG là trung trực của OL nên J là trung điểm của OL và $\angle GJO=90^o$
Lại có: $\angle JGF=\angle GFO=90^o \Rightarrow$ OFGJ là hình chữ nhật.
$\Rightarrow OL=2JO=2GF=2|BF-BG|=|2BF-2BG|$
Do O là tâm đường tròn ngoại tiếp của $\vartriangle ABC$ và $FO \perp AB \Rightarrow$ F là trung điểm của BA nên $2BF=BA$.
Vẽ $IK \perp BC$ tại K thì G,K,N là tiếp điểm của đường tròn tâm I nội tiếp $\vartriangle ABC$ với các cạnh $\vartriangle ABC$. Suy ra $BG=BK;CK=CN;AG=AN$.
Mặt khác
$2BG=BG+BK=BA-AG+CB-CK=BA+BC-(AN+CN)=BA+BC-CA$
$\Rightarrow OL=|BA-(BA+BC-CA)|=CA-CB=CA-CD=AD$. Tương tự $OM=AE$.
Lại có: $\angle OFA+\angle OHA=90^o+90^o=180^o \Rightarrow \angle FAH+\angle FOH=180^o$
$\Rightarrow \angle FAH=180^o-\angle FOH=180^o-(360^o-\angle FOJ-\angle MOL-\angle MOH)=\angle MOL$
Do đó $\vartriangle MOL=\vartriangle EAD(c.g.c)$.
Do cách dựng hình nên I là tâm đường tròn ngoại tiếp $\vartriangle MOL$.
Từ đó, ta có đpcm.
Lời giải 2:

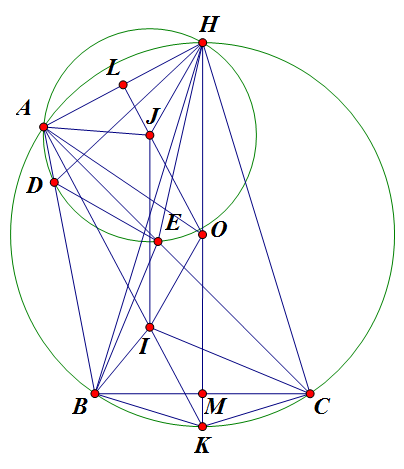
Không mất tính tổng quát, giả sử $BC \leq AB \leq AC$ (do BC là cạnh nhỏ nhất trong 3 cạnh $\vartriangle ABC$)
Gọi I,O thứ tự là tâm đường tròn nội tiếp, ngoại tiếp $\vartriangle ABC$.
Gọi J là tâm đường tròn ngoại tiếp $\vartriangle AED$.
Yêu cầu bài toán trở thành: Chứng minh $JA=OI$ (*)
Trên cung BC của đường tròn tâm O chứa A, lấy H là điểm chính giữa $\Rightarrow HB=HC$.
Đường tròn I nội tiếp $\vartriangle ABC$ tiếp xúc BC tại M.
Vẽ AI cắt cung BC không chứa A tại K.
$\angle KAB=\angle KAC \Rightarrow KB=KC$. Mà HB=HC nên HK là trung trực của BC.
Vẽ HK cắt BC tại M thì M là trung điểm BC và $KM \perp BC$.
Lại có OB=OC nên O thuộc trung trực BC hay H,O,K thẳng hàng. (1)
Xét $\vartriangle HBD$ và $\vartriangle HCE$, ta có:
HB=HC; BD=CE; $\angle HBD=\angle HCE$ (cùng chắn cung HD)
$\Rightarrow \vartriangle HBD=\vartriangle HCE (c.g.c) \Rightarrow \angle HDB=\angle HEC$
$\Rightarrow 180^o-\angle HDB=180^o-\angle HEC \Rightarrow \angle HDA=\angle HEA$
Nên HADE là tứ giác nội tiếp. $\Rightarrow JA=JH$. Mà OA=OH nên JO là trung trực của HA.
Vẽ JO cắt HA tại L thì L là trung điểm của HA và $JO \perp HA$.
Mặt khác, JA=JH nên JL là phân giác góc HJA $\Rightarrow \angle LJA=\dfrac{1}{2}\angle HJA$
Lại có: HK là đường kính (do (1)) nên $\angle HAK=90^o \Rightarrow AK \perp HA$
$\Rightarrow JO \parallel AK$ (2)
$\angle KIC=\angle IAC+\angle ICA=\dfrac{1}{2}\angle BAC+\dfrac{1}{2}\angle BCA$ (3)
$\angle KCB=\angle KAC=\dfrac{1}{2}\angle BAC$ (do cùng chắn cung KB) nên
$\angle KCI=\angle KCB+\angle ICB=\dfrac{1}{2}\angle BAC+\dfrac{1}{2}\angle ACB$ (4)
Từ (3), (4) suy ra $\vartriangle KIC$ cân tại K nên $KI=KC$.
Ta có:
$\begin{array}{l}
\angle CHK = \angle CAK = \frac{1}{2}\angle BAC = \angle KCB \\
\Leftrightarrow \cos CHK = \cos KCB \\
\Leftrightarrow \frac{{HC}}{{HK}} = \frac{{CN}}{{CK}} \Leftrightarrow \frac{{HC}}{{2KO}} = \frac{1}{2}.\frac{{BC}}{{KC}} \Leftrightarrow \frac{{HC}}{{KO}} = \frac{{BC}}{{KC}} = \frac{{CE}}{{KI}} \\
\end{array}$
$\Rightarrow \vartriangle OIK \sim \vartriangle HEC (c.g.c)$
$\Rightarrow \angle OIK=\angle HEC \Rightarrow 180^o-\angle OIK=180^o-\angle HEC$
$\Rightarrow \angle OIA=\angle HEA=\dfrac{1}{2}\angle HJA=\angle LJA$
$\Rightarrow$ JOIA là tứ giác nội tiếp. Lại do (2) nên JOIA là hình thang cân.
Suy ra JA=OI nên (*) đúng. Ta có đpcm.
_____________________________________________________________________
@Trọng tài: Lời giải 2 hợp lý hơn

Điểm: 6/6

Bài viết đã được chỉnh sửa nội dung bởi hxthanh: 23-06-2012 - 16:55

[Trần Đức Anh @@]

Chém gì đến hai cách dữ thế

Bài viết đã được chỉnh sửa nội dung bởi Trần Đức Anh @@: 17-02-2012 - 16:29

[perfectstrong]

Perfectstrong đội Gama xin giải quyết bài 1 đội Beta.
Lời giải:
ĐKXĐ: $x,y,z$ đôi một khác nhau và khác 0.
Ta có:
\[\begin{array}{l}
\sum {\frac{{2{x^2} + xy + yz + xz}}{{\left( {x - y} \right)\left( {x - z} \right)}}} = 2\sum {\frac{{{x^2}}}{{\left( {x - y} \right)\left( {x - z} \right)}}} + \left( {xy + yz + xz} \right)\left( {\sum {\frac{1}{{\left( {x - y} \right)\left( {x - z} \right)}}} } \right) \\
= 2\sum {\frac{{{x^2}}}{{\left( {x - y} \right)\left( {x - z} \right)}}} + \left( {xy + yz + xz} \right).\frac{{z - y + x - z + y - x}}{{\left( {x - y} \right)\left( {y - z} \right)\left( {z - x} \right)}} = 2\sum {\frac{{{x^2}}}{{\left( {x - y} \right)\left( {x - z} \right)}}} \\
\sum {\frac{{{x^2}}}{{\left( {x - y} \right)\left( {x - z} \right)}}} = \frac{{{x^2}\left( {z - y} \right) + {y^2}\left( {x - z} \right) + {z^2}\left( {y - x} \right)}}{{\left( {x - y} \right)\left( {y - z} \right)\left( {z - x} \right)}} = \frac{{zx\left( {x - z} \right) + y\left( {{z^2} - {x^2}} \right) + {y^2}\left( {x - z} \right)}}{{\left( {x - y} \right)\left( {y - z} \right)\left( {z - x} \right)}} \\
= \frac{{\left( {z - x} \right)\left( { - zx + yz + yx - {y^2}} \right)}}{{\left( {x - y} \right)\left( {y - z} \right)\left( {z - x} \right)}} = \frac{{\left( {z - x} \right)\left( {x - y} \right)\left( {y - z} \right)}}{{\left( {z - x} \right)\left( {y - z} \right)\left( {z - x} \right)}} = 1 \\
\end{array}\]
Do đó, hệ phương trình đã cho tương đương với:
\[\left\{ \begin{array}{l}
\frac{1}{{xy}} + \frac{1}{{yz}} + \frac{1}{{xz}} = 1{\rm{ }}\left( 1 \right) \\
3\left( {x + \frac{1}{x}} \right) = 4\left( {y + \frac{1}{y}} \right) = 6\left( {z + \frac{1}{z}} \right){\rm{ }}\left( 2 \right) \\
\end{array} \right.\]

\[\left( 1 \right) \Leftrightarrow x + y + z = xyz \Leftrightarrow z\left( {xy - 1} \right) = x + y\]
Nếu $xy=1 \Rightarrow x+y=0 \Rightarrow x=-y$. Thế vào lại, ta có: $-x^2=1$: vô nghiệm $x$
Nên $xy \neq 1 \Rightarrow z=\dfrac{x+y}{xy-1}$. Do $z \neq 0 \Rightarrow x+y \neq 0 \Rightarrow x \neq -y$ (3)
\[\begin{array}{l}
z + \frac{1}{z} = \frac{{x + y}}{{xy - 1}} + \frac{{xy - 1}}{{x + y}} = \frac{{\left( {1 + {x^2}} \right)\left( {1 + {y^2}} \right)}}{{\left( {xy - 1} \right)\left( {x + y} \right)}} \\
\left( 2 \right) \Rightarrow 3\left( {x + \frac{1}{x}} \right) = 6.\frac{{\left( {1 + {x^2}} \right)\left( {1 + {y^2}} \right)}}{{\left( {xy - 1} \right)\left( {x + y} \right)}} \Leftrightarrow 2.\frac{{\left( {1 + {x^2}} \right)\left( {1 + {y^2}} \right)}}{{\left( {xy - 1} \right)\left( {x + y} \right)}} - \frac{{{x^2} + 1}}{x} = 0 \\
\Leftrightarrow \frac{{\left( {{x^2} + 1} \right)\left[ {\left( {2 + 2{y^2}} \right)x - \left( {xy - 1} \right)\left( {x + y} \right)} \right]}}{{x\left( {xy - 1} \right)\left( {x + y} \right)}} = 0 \Leftrightarrow {x^2}y - x{y^2} - 3x - y = 0 \\
\left( 2 \right) \Rightarrow 4\left( {y + \frac{1}{y}} \right) = 6.\frac{{\left( {1 + {x^2}} \right)\left( {1 + {y^2}} \right)}}{{\left( {xy - 1} \right)\left( {x + y} \right)}} \Leftrightarrow 3.\frac{{\left( {1 + {x^2}} \right)\left( {1 + {y^2}} \right)}}{{\left( {xy - 1} \right)\left( {x + y} \right)}} - 2.\frac{{{y^2} + 1}}{y} = 0 \\
\Leftrightarrow \frac{{\left( {{y^2} + 1} \right)\left[ {3y\left( {1 + {x^2}} \right) - 2\left( {xy - 1} \right)\left( {x + y} \right)} \right]}}{{y\left( {x + y} \right)\left( {xy - 1} \right)}} = 0 \Leftrightarrow {x^2}y - 2x{y^2} + 2x + 5y = 0 \\
\end{array}\]
Từ (2), ta có hệ phương trình sau:
\[\left\{ \begin{array}{l}
{x^2}y - x{y^2} - 3x - y = 0 \\
{x^2}y - 2x{y^2} + 2x + 5y = 0 \\
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
x{y^2} - 5x - 6y = 0 \\
{x^2}y - 8x - 7y = 0 \\
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
x{y^2} = 5x + 6y{\rm{ }}\left( 4 \right) \\
{x^2}y = 8x + 7y{\rm{ }}\left( 5 \right) \\
\end{array} \right.\]
Do $x,y \neq 0 \Rightarrow 8x+7y \neq 0$ (theo (5))
\[\begin{array}{l}
\Rightarrow \frac{{5x + 6y}}{{8x + 7y}} = \frac{{x{y^2}}}{{{x^2}y}} = \frac{y}{x} \Rightarrow 5{x^2} + 6xy = 8xy + 7{y^2} \Leftrightarrow 5{x^2} - 2xy - 7{y^2} = 0 \\
\Leftrightarrow \left( {x + y} \right)\left( {5x - 7y} \right) = 0 \Leftrightarrow 5x - 7y = 0 \Leftrightarrow x = \frac{7}{5}y\left( {do\left( 3 \right)} \right) \\
\end{array}\]
Thế lại vào (4), ta có:
\[\frac{7}{5}{y^3} = 13y \Leftrightarrow {y^2} = \frac{{65}}{7} \Leftrightarrow \left[ \begin{array}{l}
y = \sqrt {\frac{{65}}{7}} \Rightarrow x = \sqrt {\frac{{91}}{5}} \Rightarrow z = \sqrt {\frac{{13}}{{35}}} :True \\
y = - \sqrt {\frac{{65}}{7}} \Rightarrow x = - \sqrt {\frac{{91}}{5}} \Rightarrow z = - \sqrt {\frac{{13}}{{35}}} :True \\
\end{array} \right.\]
Vậy, hệ có nghiệm:
\[\left( {x;y;z} \right) \in \left\{ {\left( {\sqrt {\frac{{91}}{5}} ;\sqrt {\frac{{65}}{7}} ;\sqrt {\frac{{13}}{{35}}} } \right);\left( { - \sqrt {\frac{{91}}{5}} ; - \sqrt {\frac{{65}}{7}} ; - \sqrt {\frac{{13}}{{35}}} } \right)} \right\}\]
_____________________________________________________________________
@Trọng tài: Lời giải đúng
Bài này lẽ ra không nên đưa vào chương trình THCS
Mấu chốt ở công thức
$\sum {\frac{{2{x^2} + xy + yz + xz}}{{\left( {x - y} \right)\left( {x - z} \right)}}} = 2$
Trọng tài cũng chịu!

Điểm 6/6

Bài viết đã được chỉnh sửa nội dung bởi hxthanh: 23-06-2012 - 17:07

[PSW]

Hân hăng hái quá nhỉ

[Trần Đức Anh @@]

Hân giải cách gì khủng bố thế.

Bài viết đã được chỉnh sửa nội dung bởi Trần Đức Anh @@: 19-02-2012 - 20:48

[Zaraki]

ĐỀ ĐỘI GAMA

Bài 1. Giải hệ phương trình
$$\left\{\begin{matrix}x^4-y^4=240 & & \\x^3-2y^3=3x^2-12y^2-4x+32y & &\end{matrix}\right.$$
Bài 2. Xét trên mặt phẳng tọa độ $Oxy$. Quy ước: điểm nguyên là điểm có hoành độ và tung độ nguyên.
a) Tồn tại hay không một điểm $A$ sao cho khoảng từ $A$ đến các điểm nguyên trên mặt phẳng là khác nhau đôi một ?
b) Tồn tại hay không một đường tròn trên mặt phẳng chứa đúng $2012$ điểm nguyên ?

Bài 3. Cho $x_1,x_2,...,x_n$ là các số thực phân biệt $(n \ge 2)$. Chứng minh rằng
$$\sum_{k=1}^{n} \dfrac{ \left ( 1+x_k^2 \right )^{n/2}}{\prod_{j=1, j \ne k}^{n} \left | x_k-x_j \right |} \ge n.$$

Bài 4. Cho $2$ đường trong tiếp xúc ngoài nhau lần lượt là $(O;9 \ \text{cm}); \ (I;3 \ \text{cm}).$ Biết $(O)$ và $(I)$ chẵn một đoạn thẳng thành $3$ đoạn thẳng bằng nhau. TÍnh độ dài mỗi đoạn chắn.

Bài 5. Một học sinh vẽ trên mặt phẳng một số đường tròn cùng tất cả các tiếp tuyến chung có thể của mỗi cặp đường tròn trong số các đường tròn đã vẽ. Biết rằng các tiếp tuyến vẽ chứa tất cả $2011$ cạnh của một đa giác đều có $2011$ đỉnh. Hỏi số đường tròn học sinh vẽ tối thiểu là bao nhiêu ?

Bài 6. Với mỗi $n \in \mathbb{N}^*$, kí hiệu $\varphi (n)$ là các số nguyên dương không vượt quá $n$ và nguyên tố cùng nhau với $n$.
Cho $a,b,c \in \mathbb{N}^*; b \ne c$. Chứng minh rằng $2a \mid \varphi (b^a+c^a).$

[hoangkhtn2010]

hoangkhtn2010 của đội Gamma giải bài 6 đội Beta:
Lời giải:
Kí hiệu $r$ là bán kính đường tròn nội tiếp tam giác $ABC$ có tâm là $I$; $A_1,B_1,C_1$ là tiếp điểm của $(I)$ với các cạnh của tam giác ban đầu $T_0$ (ta kí hiệu $T_0$ bằng tam giác $ABC$ để tiện theo dõi).
Ta tính như sau:
$2p_1=B_1C_1+C_1A_1+A_1B_1
= 2r(\sum \cos \angle B_1C_1I)
= 2r(\sum \cos \frac{A}{2})$
Ngoài ra $p_0=r.\left(\sum \frac{1}{\tan\frac{A}{2}}\right)$. Do $\sum \tan\frac{A}{2}\tan\frac{B}{2}=1$ nên ta có \[2p_1=2p_0\prod\tan\frac{A}{2}.\left(\sum \cos \frac{A}{2}\right)\]
Theo các bất đẳng thức quen thuộc, ta có
$$\prod\tan\frac{A}{2}\le\frac{1}{3\sqrt{3}}, (1)$$
$$\sum\cos\frac{A}{2}\le \frac{3\sqrt{3}}{2}. (2)$$
Vì vậy $2p_1\le 2p_0.\frac{1}{3\sqrt{3}}.\frac{3\sqrt{3}}{2}=p_0$. Do đó $p_1\le \frac{p_0}{2}$.
Chứng minh một cách tương tự ta suy ra $p_n\le \frac{p_0}{2^n}$.
Vậy thì \[
\sum\limits_{i = 1}^n {p_i } \le \sum\limits_{i = 1}^n {\frac{{p_0 }}{{2^i }}} = \left( {1 - \frac{1}{{2^n }}} \right)p_0 < p_0
\]
Mặt khác, khi xét bất đẳng thức \[
\sum\limits_{i = 1}^n {p_i } \le \sum\limits_{i = 1}^n {\frac{{p_0 }}{{2^i }}} = \left( {1 - \frac{1}{{2^n }}} \right)p_0
,\]
ta chuyển qua giới hạn khi $n$ tiến đến $+\infty$ ta có $\lim_{n\to +\infty} \sum_{i=1}^np_i\le p_0$.
Dấu bằng xảy ra khi và chỉ khi dấu bằng trong hai bất đẳng thức (1) và (2) xảy ra, nghĩa là tam giác $T_0$ đều.
Bài toán chứng minh xong.
**Chứng minh hai bất đẳng thức (1) và (2)**
a. Chứng minh bất đẳng thức (1):
Theo trên, do $\sum \tan\frac{A}{2}\tan\frac{B}{2}=1$ nên áp dụng bất đẳng thức Cauchy ta có:

\[
1 = \sum {\tan \frac{A}{2}\tan \frac{B}{2}} \ge 3\left( {\tan \frac{A}{2}\tan \frac{B}{2}\tan \frac{C}{2}} \right)^{\frac{2}{3}} \Rightarrow \tan \frac{A}{2}\tan \frac{B}{2}\tan \frac{C}{2} \le \frac{1}{{3\sqrt 3 }}
\]
Vậy bất đẳng thức (1) chứng minh xong.
b. Chứng minh bất đẳng thức (2): Xét hàm số $f(x)=\cos x$ có $f''(x)=-\cos x \le 0$ với mọi $x\in\left[0;\frac{\pi}{2}\right]$ nên $f(x)$ là hàm lõm trên $\left[0;\frac{\pi}{2}\right]$. Áp dụng bất đẳng thức Jensen cho $x$ lần lượt là $\frac{A}{2},\frac{B}{2},\frac{C}{2}$ ta có:

\[
\sum {\cos \frac{A}{2}} \le 3\cos \frac{{\sum {\frac{A}{2}} }}{3} = 3\cos \frac{\pi }{6} = \frac{{3\sqrt 3 }}{2}
\]
Bất đẳng thức (2) chứng minh xong.
Dẫu bằng ở cả hai bất đẳng thức trên xảy ra khi và chỉ khi tam giác $ABC$ đều.
________________________________________________________________
@ Trọng tài: Cách làm hay!

Điểm: 8/8

Bài viết đã được chỉnh sửa nội dung bởi hxthanh: 23-06-2012 - 21:41

[NguyThang khtn]

Sặc, đã Thái Phúc rồi lại thêm anh Hoàng-KHTN vào thì GAMA bá đạo quá!
p/s: Cặp đôi song sát!

[Trần Đức Anh @@]

Thầy Định sao im lặng thế, bắn pháo hoa đi chứ

[Ispectorgadget]

Thầy Định sao im lặng thế, bắn pháo hoa đi chứ

Thầy Định đang bị bệnh mà cứ chờ xem sao đã

Bài viết đã được chỉnh sửa nội dung bởi Ispectorgadget: 19-02-2012 - 18:25

[Trần Đức Anh @@]

Trần Đức Anh @@ của đội BETA xin giải bài olympiad của đội GAMA:
Ta thấy rằng: $x|y$ $\rightarrow$ $\varphi{(x)}|\varphi{(y)}$.Do đó ta có thể đặt $(b,c)=1$ $(b\neq{c})$. Đặt $S=b^a+c^a$ và $m\equiv (\frac{b}{c})$ (mod $S$). Từ $(b,S)=(c,S)=1$ ta có: $(m,S)=1$. Vì vậy, $k\in\mathbb{N}$: $S|m^k+1$ suy ra $S|b^k+c^k$, suy ra $k\geq a$. Ta có: $S|m^k+1$ thì $k=a$ là giá trị tự nhiên nhỏ nhất thảo mãn $S|m^k+1$ $(1)$.
Kí hiệu $q=ord_{s}(m)$, ta có: $S|m^q-1$ suy ra $S|b^q-c^q$ suy ra $b^a+c^a=S<b^q+c^q$ suy ra $a<q$.
Nếu $q<2a$, ta viết $m^q=m^a.m^{q-a}$, ta có: $m^{q-a}\equiv{-1}$ (mod $S$), mà không thỏa mãn $(1)$ và $q-a<a$. Do đó $q\geq{2a}$ ta có $S|m^a-1$. Vì vậy $ord_s(m)=2a$. Bởi vì $m^{\varphi(b^a+c^a)}\equiv{1}$ (mod $S$).
Suy ra $2a|\varphi{b^a+c^a}$. ĐPCM.
______________________________________________________
@Trong tài: Nice Solution!
Tuy còn một số chỗ trình bày không hợp lý, (cấp và ký hiệu Legendre có phải giải thích không nhỉ?) và lỗi $\LaTeX$
Đức Anh thật là nguy hiểm

Điểm: 8/8

Bài viết đã được chỉnh sửa nội dung bởi hxthanh: 23-06-2012 - 21:41

[hoangkhtn2010]

Bạn xem lại đoạn $x\mid y\to \varphi(x)\mid \varphi(y)$? Có vẻ kết quả này không hiển nhiên lắm ?