Bài 90: Cho 2 đường tròn (O) và (O') cắt nhau tại A và B cố định((O) và (O') ở ngoài nhau).P là 1 điểm di động trên cung lớn AB trên (O).PA,PB cắt (O') lần lượt tại C,D sao cho C,D thuộc cung lớn AB của (O').Từ O' vẽ O'E vuông góc CD tại E.
CMR: PE luôn đi qua 1 điểm cố định khi P di động trên cung lớn AB.
P/s:Đề cực ngắn nhưng chứng minh không ngắn như cái đề  ,có thể là dài hơn bài 83 đã khiến em Black "nổ não" và lần này sẽ "nổ" lần 2
,có thể là dài hơn bài 83 đã khiến em Black "nổ não" và lần này sẽ "nổ" lần 2 
_________________
Bổ đề: Cho $\triangle ABC$ nội tiếp $(O)$, kẻ tiếp tuyến tại $B$ và $C$ cắt nhau tại $E$; trung tuyến $AF$, khi đó ta có $\angle BAE = \angle CAF$.
Để chứng minh bổ đề này, ta dùng tới 2 khái niệm
* Đường đẳng giác: Cho góc $xOy$, ta nói 2 đường thẳng $d_1$ và $d_2$ là đường đẳng giác trong góc nếu chúng cùng đi qua đỉnh $O$ là đối xứng với nhau qua tia phân giác của góc.
~> Chứng minh, ta nhắc đến tiêu chuẩn của một đường đẳng giác:Tiêu chuẩn này gắn liền với định lý Steiner: Cho $\triangle ABC$ và 2 điểm $D,E$ trên cạnh $BC$. Khi đó, $AD$ và $AE$ là 2 đường đẳng giác của $\angle BAC$ khi vả chỉ khi:
$$\frac{BD}{DC} . \frac{BE}{EC} = \frac{AB^2}{AC^2}$$ (*)
- Chứng minh định lý này:
 + Phần thuận:
+ Phần thuận:Giả sử $AD$ và $AE$ là 2 đường đẳng giác của $\angle BAC$ ta sẽ chứng minh đẳng thức (*) thỏa mãn. Thật vậy, ta có:
$\frac{BD}{DC} = \frac{S_{BAD}}{S_{DAC}} = \frac{AD.AB.\sin\angle BAD}{AD.AC.\sin\angle DAC} = \frac{AB}{AC}. \frac{\sin\angle BAD}{\sin\angle DAC}$
Tương tự, ta cũng có:
$\frac{BE}{EC} = \frac{AB}{AC}.\frac{\sin\angle BAE}{\sin\angle EAC}$
Mặt khác, do $AD$ và $AE$ là 2 đường đẳng giác nên ta có:
$\angle BAD = \angle EAC; \angle DAC = \angle BAE$
Kết hợp những điều trên lại, ta có (*).
+Phần đảo: Giả sử thỏa mãn $AD$ và $AE$ thỏa (*). Vậy dựng đường đẳng giác $AD'$ của $AE$. Khi đó ta có hệ thức:
$\frac{BD'}{D'C}.\frac{BE}{EC} = \frac{AB^2}{AC^2}$
Mà ta đã có (*) nên $\Rightarrow \frac{BD}{DC} = \frac{BD'}{D'C}$.
$\Rightarrow D \equiv D'$.
Vậy ta đã chứng minh xong định lý Steiner.
Giờ ta đi tiếp tới một khái niệm thứ 2
*Đường đối trung: là đường đẳng giác với trung tuyến và sẽ có tính chất như những cặp đường đẳng gicá khác.
Từ tiêu chuẩn của đưởng đẳng giác hay chính là định lý Steiner ta vừa chứng minh, dễ dàng suy ra tính chất của đường đối trung như sau
Cho $\triangle ABC$. Ta có $AD$ ($D \in BC$) là đường đối trung $\Leftrightarrow \frac{DB}{DC} = \frac{AB^2}{AC^2}$
Giờ ta sẽ quay lại chứng minh bổ đề, em sẽ nhắc lại đề bài để mọi người đỡ mất công lăn lên xuống.
Cho $\triangle ABC$ nội tiếp $(O)$, tiếp tuyến tại $B$ và $C$ cắt nhau tại $E$. Trung tuyến $AF$. Ta chứng minh $\angle BAE = \angle CAF$ hay cũng chính là đi chứng minh $AE$ là đường đối trung của $\triangle ABC$
* Chứng minh: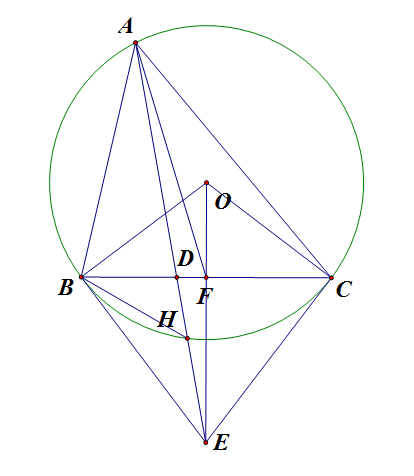
Gọi giao điểm của $AE$ và $BC$ là $D$. Ta có:
$\frac{DB}{DC} = \frac{S_{ABP}}{S_{ACP}} = \frac{AB.BP.\sin\angle ABP}{AC.CP.\sin\angle ACP}=\frac{AB}{AC}.\frac{\sin\angle ACB}{\sin\angle ABC}$
Vậy giờ ta cần chứng minh $\sin\angle ABP = \sin\angle ACB; \sin\angle ACP = \sin\angle ABC$
Thật vậy, cho $AE \cap (O) = H$ thì ta có:
$\angle EBA = \angle BHE = 180^o - \angle BHA = 180^o - \angle BCA$
Vậy $\angle EBA$ bù $\angle BCA$. Vậy $\sin$ 2 góc sẽ bằng nhau, chứng minh tương tự ta cũng có $\sin\angle ACP = \sin\angle ABC$.
Vậy $\frac{DB}{DC} = \frac{AB^2}{AC^2}$
Theo tiêu chuẩn của đường đối trung, ta có $AE$ là đường đối trung của $\angle BAC$
$\Rightarrow \angle BAE = \angle CAF$
__________________________________
Chứng minh các yếu tố phụ mệt nhoài, ta quay trở lại bài toán:

Gọi giao của 2 tiếp tuyến tại $A$ và $B$ của $(O)$ là $I$. $M$ là trung điểm $AB$
Áp dụng bổ đề vừa chứng minh, ta có $\angle API = \angle BPM$ (1)
Mặt khác, dễ dàng chứng minh $\triangle PAB \sim \triangle ADC$
$\Rightarrow \frac{PB}{PC} = \frac{AB}{DC} = \frac{BM}{EC}$
Dễ thấy, 2 tam giác đồng dạng thì tỉ số đường trung tuyến xuất phát từ 2 đỉnh tương ứng của 2 tam giác cũng bằng tỉ số đồng dạng. Tức:
$\frac{PB}{PC} = \frac{AM}{PE} = \frac{BM}{EC}$
$\Rightarrow \angle BPM = \angle CPE$ (2)
Từ $(1)$ và $(2) \Rightarrow P,I,E:\text{thẳng hàng}$.
Mặt khác, do $A,B:const \Rightarrow I:const$
Vậy $PE$ đi qua điểm cố định chính là $I$.
Bài toán đã được chứng minh HOÀN TOÀN.
Edited by BlackSelena, 09-08-2012 - 13:36.
, thiếu hẳn 1 điểm cố dịnh và em đã tìm ra
, em sẽ làm thêm nhanh nhất có thể

















