Chủ đề này có 23 trả lời

[daothanhoai]

Lời giới thiệu:

Những bài hình sau đây đều được tôi sáng tạo qua việc vẽ Autocad. Tôi cũng thừa nhận hiện nay do không làm việc trên lĩnh vực toán, và cũng bận nên tôi chưa có thời gian nghiên cứu sâu về bài toán. Tôi đưa lên diễn đàn mong được các bạn cùng chứng minh hoặc chỉ giúp đó là vấn đề nào, bài toán hình học nào. Bất kỳ bài toán nào tôi phát hiện ra nếu như lặp lại các bài toán đã có sẽ đều bị tôi xóa nếu như biết được điều đó. Chân thành cảm ơn

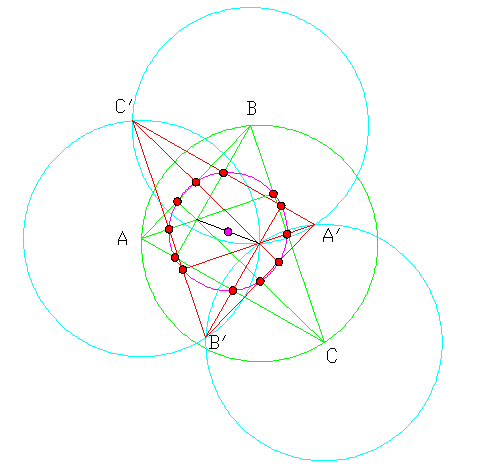
Bài 1: Đã được ẩn lý do có thể chứng minh được bằng kết quả của định Lý Napoleon

Bài viết đã được chỉnh sửa nội dung bởi daothanhoai: 09-09-2012 - 22:40

[daothanhoai]

Bài 2: Cho tam giác ABC nhọn và đường tròn ngoại tam giác. Vẽ đường tròn tâm A, tâm B, tâm C, bán kính bằng bán kính đường tròn ngoại tiếp tam giác. Khi đó sẽ xác định được sáu cặp tam giác đều gọi là tam giác đều to và tam giác đều nhỏ. Chứng minh rằng trọng tâm của các cặp tam giác đều to và trọng tâm của các cặp tam giác đều nhỏ tạo thành hai tam giác đều.(Trên hình vẽ chỉ thể hiện 3 tam giác đều nhỏ)

Hình gửi kèm

• 

Bài viết đã được chỉnh sửa nội dung bởi daothanhoai: 19-08-2012 - 20:09

[daothanhoai]

Bài 3: Ba đường tròn tâm A,B,C giao nhau. Trục đẳng phương của từng cặp đường tròn tạo thành các góc 60 độ <=> $\Delta ABC$ là tam giác đều.

Bài 4: Cho tam giác ABC, ba điểm $A',B',C'$ thuộc ba cạnh của tam giác ABC và $A'',B'',C''$ thuộc ba cạnh của tam giác $A'B'C'$. Biết $A'A'',B'B'',C'C''$ đồng quy. Khi đó ta có: $AA',BB',CC'$ đồng quy khi và chỉ khi $AA'',BB'',CC''$ đồng quy.

Bài 5: Ẩn do có thể chứng minh được bằng kết quả liên quan đến định lý Napoleon

Hình gửi kèm

• 
• 

Bài viết đã được chỉnh sửa nội dung bởi daothanhoai: 10-09-2012 - 10:15

[daothanhoai]

Bài 7: Cho một điểm H và một đường tròn tâm O. Từ H kẻ hai đường thẳng a,b cắt đường tròn tại bốn điểm: A,B,C,D khi đó AB giao với CD tại N. BC giao với AD tại M. Khi đó MN là một đường thẳng cố định không phụ thuộc vào hai đường thẳng a,b ở trên. (Qua kết quả đối chiếu thì bài bảy không phải là hệ quả của định lý Pascal)

Hệ quả 1: Một đa giác 2n cạnh nội tiếp và có các đường chéo đồng quy ta sẽ vẽ được n(n-1) điểm thẳng hàng

Hệ quả 2: (Hình vẽ về các điểm thẳng hàng tạo bởi tiếp tuyến và các cặp cạnh của một tứ giác nội tiếp-giống hệ quả của Pascal nhưng cách tiếp cận của Pascal là từ cạnh của lục giác suy biến; cách tiếp cận của giải quyết hệ quả này là đường chéo suy biến)

Hình gửi kèm

• 

Bài viết đã được chỉnh sửa nội dung bởi daothanhoai: 08-09-2012 - 08:14

[daothanhoai]

Bài 8: Phát biểu tương tự bài 7 nhưng thay đường tròn bởi cặp đường thẳng.

a, Cho điểm I và hai đường thẳng. Qua điểm I kẻ ba đường thẳng cắt hai đường thẳng ban đầu tại A,B,C và A'B'C'. Nối các điểm như hình vẽ khi đó ta có kết quả là ba điểm MNP thẳng hàng(chỉ dừng ở đây thì chỉ là hệ quả của Pappus theorem). Nhưng đường thẳng M,N,P là cố định và nó đi qua giao điểm của hai đường thẳng ban đầu.

b, Chứng minh mọi đường thẳng đi qua I cắt hai đường thẳng ban đầu và đường thẳng tạo bởi phưởng pháp làm ở trên(đường thẳng M,N,P) tại 3 điểm J,K,H như hình vẽ khi đó J,K,I,H sẽ tạo thành hàng điểm điều hòa

Hình gửi kèm

• 

Bài viết đã được chỉnh sửa nội dung bởi daothanhoai: 07-09-2012 - 10:51

[daothanhoai]

Bài 9: Tâm của đường tròn O nằm trên đường tròn I. A,D thuộc O và B,C thuộc I sao cho AB và CD là tiếp tuyến chung của hai đường tròn. Trục đẳng phương của hai đường tròn cắt AB,CD tại M và N ta có

1-MA=MB và NC=ND.
2-BC là tiếp tuyến của đường tròn tâm O

Hình gửi kèm

• 

Bài viết đã được chỉnh sửa nội dung bởi daothanhoai: 07-09-2012 - 10:51

[daothanhoai]

Bài 10: Cho tam giác ABC ngoại tiếp đường tròn tâm I. Đường tròn tâm O ngoại tiếp tam giác BCI.
1-Chứng minh rằng O,I,A thẳng hàng.
2-Tâm Đường tròn bàng tiếp tam giác Ứng với góc A cũng thẳng hàng với O, I và nằm trên đường tròn tâm O.

Hình gửi kèm

• 

Bài viết đã được chỉnh sửa nội dung bởi daothanhoai: 07-09-2012 - 18:17

[perfectstrong]

Bài 10: Cho tam giác ABC ngoại tiếp đường tròn tâm I. Đường tròn tâm O ngoại tiếp tam giác BCI. Chứng minh rằng O,I,A thẳng hàng

Bài này không khó
Lời giải:
\[
\begin{array}{l}
\angle OIC = 90^o - \frac{{\angle COI}}{2} = 90^o - \angle IBC \\
\angle AIC = 180^o - \left( {\angle IAC + \angle ICA} \right) = 180^o - \frac{{\angle BCA + \angle ACB}}{2} = 180^o - \frac{{180^o - \angle ABC}}{2} = 90^o + \angle IBC \\
\Rightarrow \angle OIC + \angle AIC = 180^o \Rightarrow Q.E.D \\
\end{array}
\]

[daothanhoai]

Bài 6 bị xóa, lý do lặp lại: http://www.cut-the-k...Thebault1.shtml

Bài viết đã được chỉnh sửa nội dung bởi daothanhoai: 08-09-2012 - 08:27

[daothanhoai]

Bài 11: Hai đường tròn giao nhau, khi đó một đường thẳng bất kỳ cắt trục đẳng phương và cắt các đường tròn tại các điểm M, A,B,A',B' như hình vẽ.

Khi đó ta có các đoạn thẳng tỉ lệ: $\frac{MA}{MB}=\frac{MA'}{MB'}$

Hình gửi kèm

• 

Bài viết đã được chỉnh sửa nội dung bởi daothanhoai: 08-09-2012 - 11:11

[perfectstrong]

Bài 11: Hai đường tròn giao nhau, khi đó một đường thẳng bất kỳ cắt trục đẳng phương và cắt các đường tròn tại các điểm M, A,B,A',B' như hình vẽ.

Khi đó ta có các đoạn thẳng tỉ lệ: $\frac{MA}{MB}=\frac{MA'}{MB'}$

Vẽ 2 đường tròn cắt nhau ở $X,Y$.
Khi đó, theo tính chất phương tích:
\[
\overline {MX} .\overline {MY} = \overline {MB} .\overline {MA'} = \overline {MA} .\overline {MB'} \Rightarrow \frac{{\overline {MA} }}{{\overline {MB} }} = \frac{{\overline {MA'} }}{{\overline {MB'} }}
\]

[daothanhoai]

Bổ đề để chứng minh bài 2:

Cho đoạn thẳng AB. Từ một điểm O bất kỳ trên trung trực của AB vẽ đường tròn bán kính OA. Sau đó vẽ đường tròn tâm A, tâm B bán kính AO, BO. Giao điểm của các đường tròn này tạo thành tam giác đều DEF như hình vẽ. Chứng minh trọng tâm tam giác DEF trùng trọng tâm tam giác AMB(cách dựng như hình vẽ) nghĩa là trọng tâm tam giác DEF cố định . Do vậy tam giác đều dựng được từ bài hai chính là tam giác đều dựng được theo định lý Napoleon

Hình gửi kèm

• 

Bài viết đã được chỉnh sửa nội dung bởi daothanhoai: 10-09-2012 - 13:49

[daothanhoai]

Bài 12: Cho đoạn thẳng AB;hai điểm M và M' cùng nửa bờ của mặt phẳng. Dựng các tam giác đều nhận các các đoạn thẳng MA,MB, M'A và M'B làm cạnh như hình vẽ. Các đỉnh tam giác đều này là D,E và D',E' như hình vẽ. Chứng minh rằng ba đường thẳng DD', EE', và đường trung bình của tam giác MM'O ứng với cạnh MM' là tam giác đều.

Hình gửi kèm

• 

[perfectstrong]

Bài 12: Cho đoạn thẳng AB;hai điểm M và M' cùng nửa bờ của mặt phẳng. Dựng các tam giác đều nhận các các đoạn thẳng MA,MB, M'A và M'B làm cạnh như hình vẽ. Các đỉnh tam giác đều này là D,E và D',E' như hình vẽ. Chứng minh rằng ba đường thẳng DD', EE', và đường trung bình của tam giác MM'O ứng với cạnh MM' là tam giác đều.

Bài này không cần quan tâm đến đường trung bình $\vartriangle MM'O$ vì nó song song với $MM'$.
Chỉ cần $MM';DD';CC'$ là đủ.
Bổ đề: Xét phép quay tâm $A$, góc $\alpha$.
$Q_A^{\alpha}:X \mapsto X'; Y \mapsto Y'$ thì $(XY;X'Y')\equiv \alpha \pmod {\pi}$.
Áp dụng vào bài toán, thấy được $(MM';CC')\equiv (DD';MM') \equiv \dfrac{\pi}{3} \pmod{\pi}$. Từ đó, ta có đpcm.

[daothanhoai]

Bài 13: Tam giác ABC có O là tâm đường tròn ngoại tiếp. Vẽ ba đường tròn tâm A,B,C bán kính bằng bán kính đường tròn ngoại tiếp. Ba đường tròn này sẽ giao nhau tại ba điểm A',B',C' như hình vẽ

1- Trực tâm tam giác ABC là tâm đường tròn ngoại tiếp tam giác A'B'C' và ngược lại tâm đường tròn ngoại tiếp tam giác ABC là trực tâm tam giác A'B'C'
2-Tam giác ABC và tam giác A'B'C' đối xứng qua I là trung điểm của đoạn thẳng nối trực tâm và tâm đường tròn ngoại tiếp tam giác ABC
3-Hai tam giác này có chung đường tròn Euler-đường tròn này hiện nay được bổ sung thêm 3 điểm nữa thành đường tròn 12 điểm

Perfecstrong chứng minh giúp chú nhé

Hình gửi kèm

• 
• 

Bài viết đã được chỉnh sửa nội dung bởi daothanhoai: 11-09-2012 - 11:09

[daothanhoai]

Bài 14: Cho điểm M nằm trên đường tròn tâm O, trục đẳng phương của hai đường tròn này là AB. Một điểm C bất kì di chuyển trên đường tròn tâm O(phía không chứa điểm M so với bờ AB). Chứng minh rằng tâm đường tròn nội tiếp tam giác ABC nằm trên đường tròn tâm M.

Hình gửi kèm

• 

Bài viết đã được chỉnh sửa nội dung bởi daothanhoai: 11-09-2012 - 14:55

[dactai10a1]

Bài 14: Cho điểm M nằm trên đường tròn tâm O, trục đẳng phương của hai đường tròn này là AB. Một điểm C bất kì di chuyển trên đường tròn tâm O(phía không chứa điểm M so với bờ AB). Chứng minh rằng tâm đường tròn nội tiếp tam giác ABC nằm trên đường tròn tâm M.

Ta có MB=MA nên M là điểm chính giữa cung AB ko chứa C của (O).SUy ra CM là phân giác góc BCA
$\widehat {MBI} = \widehat {MBA} + \widehat {ABI} = \widehat {MCA} + \widehat {CBI} = \widehat {MCB} + \widehat {CBI} = \widehat {MIB}(goc - ngoai - tam - giac - BIC)$
Suy ra tam giác MBI cân tại M suy ra MB=MI,suy ra đpcm

Bài viết đã được chỉnh sửa nội dung bởi dactai10a1: 11-09-2012 - 20:37

[sunflr]

Bài 2, Bài 3, bài 13, bài 9 đã được mấy anh em đồng nghiệp của Oai chứng minh được khá dễ. Tác giả Đào Thanh Oai nhờ chuyển lời mời các em học sinh thử làm các bài này. Hiện nay chỉ còn bài 5, bài 7, bài 8 là chưa chứng minh được

Bài viết đã được chỉnh sửa nội dung bởi sunflr: 11-09-2012 - 23:15

[perfectstrong]

Bài 7: Ta có 1 bổ đề sau là hệ quả của 1 tính chất quan trọng trong tứ giác toàn phần.
Bổ đề: Cho tứ giác $ABCD$ có $AB$ cắt $CD$ tại $E$; $AD$ cắt $BC$ tại $F$; $AC$ cắt $BD$ tại $G$. Vẽ $FG$ cắt $AB,CD$ thứ tự tại $H,I$.
Khi đó $(FGHI)=-1 \Leftrightarrow (EF;EG;EA;ED)=-1$.

Dễ dàng chứng minh tính chất trên bằng Ceva và Menelaus.
Quay lại bài toán.

Gọi $d$ là đường thẳng qua $O$ sao cho $(d;OI;a;b)=-1\quad (1)$. Suy ra $d$ cố định.
Áp dụng bổ đề cho tứ giác $ABC'B'$ có $AB \cap B'C'=O; AB' \cap BC'=M \Rightarrow (OM;OI;a;b)=-1$
Mà do (1) nên $OM \equiv d \Rightarrow M \in d$.
Tương tự, ta cũng có $N,P \in d$. Câu b cũng chỉ là hệ quả của câu a.
=============================================
Còn bài 8, chú vẽ lại cho cháu hình cụ thể được không ạ? Cháu thấy nó không đúng thì phải.
Bài 5 thì cháu không thấy đề.

[khongghen]

Bài 4: được chứng minh như sau: Dễ dàng chứng minh được \[\frac{Sin\widehat{B'CC''}}{Sin\widehat{A'CC''}}=\frac{B'C''}{A'C''}.\frac{CA'}{CB'}\]
tương tự lần nữa sau đó áp dụng định lý ceva và ceva dạng Sin ta có điều phải chứng minh

Bài 7: Bốn điểm A,B,C,D không phân biệt thứ tự di động trên trên một đường tròn. Bốn điểm trên nối lại sẽ xác định được ba điểm. Nếu một trong ba điểm cố định thì đường thẳng nối hai điểm còn lại cố định.

Hình gửi kèm

• 

Bài viết đã được chỉnh sửa nội dung bởi khongghen: 14-09-2012 - 11:09