Chủ đề này có 2 trả lời

[nguyenthehoan]

Bài toán: Cho $\Delta ABC$, đường cao $BE$, $CF$ cắt nhau tại $H$. Đường thẳng $EF$ cắt $BC$

 

tại $G$.Đường thẳng $GH$ cắt đường thẳng qua $A$ song song $BC$ tại $L$. Gọi $M$ là trung điểm 

 

của $BC$.Qua $M$ vẽ tiếp tuyến với đường tròn nội tiếp $\Delta ABC$ cắt $AL$ tại $X$.

 

Chứng minh rằng $XA=XL$ $\Leftrightarrow \cos \widehat{BAC}=\frac{b+c}{2a+b+c}$

 

P/S:Bài toán khá hay nên mời mọi người cùng làm!!!Mình mất cả tối "bịa ra"...  

[demon311]

Hình đây ạ. Chuẩn 98%.

Nhiều khả năng H thuộc (O). Mời mọi người chúng minh

[haojack]

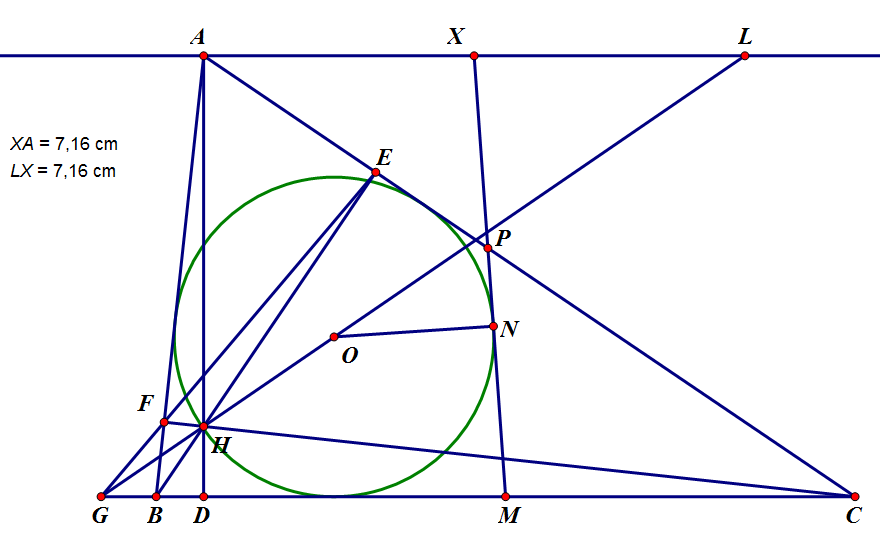
    Bổ đề: gọi $D$ là tiếp điểm của $(I)$ lên $BC$ và $DI$ cắt lại $(I)$ tại $N$, $AD$ cắt lại $(I)$ tại $P$. Đường thẳng $NP$ cắt đường thẳng nối tiếp điểm của $(I)$ lên $AB,AC$ tại $K$ thì $AK$ song song với $BC$, đồng thời điểm $X$ chính là trung điểm của $AK$.

Đây là một bổ đề có xuất hiện trên tạp chí THTT gần đây.

Trở lại bài toán, ta thấy $XA=XL$ khi và chỉ khi $L\equiv K$.

Ta sẽ tính độ dài của $AK,AL$ theo cách dựng của chúng. Không mất tính tổng quát, giả sử $AB<AC$.

* Tính $AL$:

Dễ thấy $(G,{A}',B,C)=-1$ nên \[\frac{GB}{GC}=\frac{{A}'B}{{A}'C}\Rightarrow \frac{GB}{BC}=\frac{{A}'B}{{A}'C-{A}'B}\Rightarrow GB=\frac{{A}'B\cdot BC}{{A}'C-{A}'B}\].

Do đó $G{A}'=GB+{A}'B=\frac{{A}'B\cdot BC}{{A}'C-{A}'B}+{A}'B=\frac{2{A}'B\cdot {A}'C}{{A}'C-{A}'B}=A{A}'\frac{2\cot B\cot C}{\cot C-\cot B}$.

Theo định lý Thales thì $\frac{AL}{G{A}'}=\frac{HA}{H{A}'}=\frac{\cos A}{\cos B\cdot \cos C}$ nên

$AL=\frac{\cos A}{\cos B\cdot \cos C}\cdot G{A}'=\frac{\cos A}{\cos B\cdot \cos C}A{A}'\frac{2\cot B\cot C}{\cot C-\cot B}=\frac{2\cos A\cdot A{A}'}{\sin (B-C)}$.

* Tính $AK$:

Gọi $V,W$ là tiếp điểm của $(I)$ lên $AC,AB$ và $U$ là giao điểm của $KW$ với $BC$.

Dễ thấy $(U,D,B,C)=-1$ nên tương tự trên, ta tính được $UB=\frac{DB\cdot BC}{DC-DB}$.

Do đó \[\frac{UB}{AK}=\frac{WB}{WA}\Rightarrow AK=UB\cdot \frac{WA}{WB}=\frac{DB\cdot BC}{DC-DB}\cdot \frac{WA}{WB}=\frac{BC\cdot WA}{DC-DB}\].

Từ đây, ta có $AK=AL$ khi và chỉ khi

$\frac{2\cos A\cdot A{A}'}{\sin (B-C)}=\frac{BC\cdot WA}{DC-DB}\Leftrightarrow \cos A=\frac{BC\cdot WA\sin (B-C)}{2A{A}'(DC-DB)}=\frac{a\cdot (b+c-a)\sin (B-C)}{4A{A}'(b-c)}$

Ta có $\sin (B-C)=\sin B\cos C-\sin C\cos B=\frac{1}{2R}\left( b\frac{{{a}^{2}}+{{b}^{2}}-{{c}^{2}}}{2ab}-c\frac{{{a}^{2}}+{{c}^{2}}-{{b}^{2}}}{2ac} \right)=\frac{{{b}^{2}}-{{c}^{2}}}{2Ra}$  và

$R\cdot A{A}'=\frac{2RS}{a}=\frac{abc}{2a}=\frac{bc}{2}$ nên

$\cos A=\frac{a(b+c-a)({{b}^{2}}-{{c}^{2}})}{8A{A}'(b-c)Ra}=\frac{(b+c-a)(b+c)}{8A{A}'\cdot R}=\frac{(b+c-a)(b+c)}{4bc}$.

Bài viết đã được chỉnh sửa nội dung bởi haojack: 23-02-2015 - 02:28