Bài này cũng khó nhằn đấy. Sử dụng đến 2 bài toán con.
Lời giải: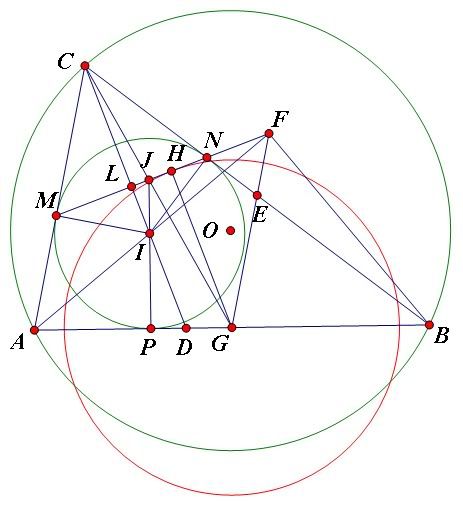
Vẽ (I) tiếp xúc AB tại P. PI cắt MN tại J. CI cắt AB tại G. CI cắt MN, AB thứ tự tại L,D. Gọi E là trung điểm BC. AI cắt BE tại F. Hạ GH
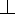
MN tại H. Ta sẽ cm 2 kết quả chính sau:
i) G là trung điểm AB.
ii) MN,AI,GE đồng quy tại F.
======================
CM=CN;IM=IN; $\angle CMJ=\angle CNJ$.
\[\dfrac{{{S_{CMJ}}}}{{{S_{CNJ}}}} = \dfrac{{\dfrac{1}{2}.CM.CJ.\sin JCM}}{{\dfrac{1}{2}.CN.CJ.\sin JCN}} = \dfrac{{\dfrac{1}{2}.MC.MJ.\sin CMJ}}{{\dfrac{1}{2}.NC.NJ.\sin CNJ}}\]
\[ \Leftrightarrow \dfrac{{\sin JCM}}{{\sin JCN}} = \dfrac{{JM}}{{JN}}\]
Lại có:
$$\angle JIM=\angle DAC;\angle JMI=\angle DCA$$
$$\Rightarrow \vartriangle JIM \sim \vartriangle DAC (g.g) \Rightarrow \dfrac{AC}{IM}=\dfrac{DC}{JM}$$
Tương tự, $$\dfrac{BC}{IN}=\dfrac{CD}{JN}$$
$$\Rightarrow \dfrac{\dfrac{CA}{IM}}{\dfrac{CB}{IN}}=\dfrac{DC}{JM}:\dfrac{DC}{JN}$$
$$\Leftrightarrow \dfrac{CA}{CB}=\dfrac{JN}{JM}=\dfrac{\sin JCN}{\sin JCM}$$
\[\dfrac{{{S_{CAG}}}}{{{S_{CBG}}}} = \dfrac{{\dfrac{1}{2}.CA.CG.\sin JMC}}{{\dfrac{1}{2}.CB.CG.\sin JNC}} = \dfrac{{CA}}{{CB}}.\dfrac{{\sin JMC}}{{\sin JNC}} = 1\]
Từ đó, có i).
Ta có:
Dễ thấy $\vartriangle FAB$ vuông tại F nên $FG=\dfrac{AB}{2}$.
\[FE = FG - GE = \dfrac{{AB - AC}}{2}\]
\[EN = BN - BE = \dfrac{{BC + BA - AC}}{2} - \dfrac{{BC}}{2} = \dfrac{{AB - AC}}{2} = FE\]
Nên $\vartriangle FEN$ cân tại F.
\[ \Rightarrow \angle FNE = \dfrac{{{{180}^0} - \angle FEN}}{2} = \dfrac{{{{180}^0} - \angle NCM}}{2} = \angle CNM\]
Suy ra được ii).
Giờ ta sẽ chứng minh GH cố định. Thật vậy:
\[\dfrac{{GH}}{{CL}} = \dfrac{{JG}}{{JC}} = \dfrac{{GF}}{{CM}} \Rightarrow GH = \dfrac{{CL}}{{CM}}.GF = \left( {\cos \dfrac{{ACB}}{2}} \right).\dfrac{{AB}}{2}\]
Suy ra, MN luôn tiếp xúc với (G;GH) cố định. (đpcm)
Bài viết đã được chỉnh sửa nội dung bởi perfectstrong: 29-10-2011 - 23:05



