Bài 1. (3 điểm)
Tìm tất cả các số nguyên dương $n$ để hai số $n + 26$ và $n – 11$ đều là lập phương của hai số nguyên dương nào đó.
Bài 2. (4 điểm)
Giả sử $a$ là một nghiệm của phương trình $\sqrt 2 {x^2} + x - 1 = 0$. không giải phương trình, hãy tính giá trị của biểu thức: $$A = \frac{{2a - 3}}{{\sqrt {2(2{a^4} - 2a + 3)} + 2{a^2}}}$$
Bài 3. (4 điểm)
a. Giải phương trình: $\sqrt {8x + 1} = {x^2} + 3x - 1$
b. Giải hệ phương trình: $\left\{ \begin{array}{l}2{x^2} - {y^2} = 1\\xy + {x^2} = 2\end{array} \right.$
Bài 4. (7 điểm)
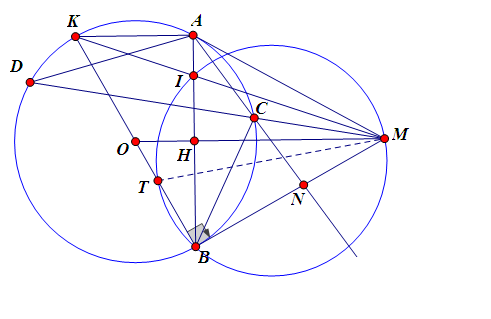
Cho đường tròn $(O;R)$ và điểm $M$ nằm ngoài đường tròn. Qua điểm $M$ vẽ hai tiếp tuyến $MA, MB$ tới đường tròn ($A$ và $B$ là các tiếp điểm). Gọi $D$ là điểm di động trên cung lớn $AB$ ($D$ không trùng $A, B$ và điểm chính giữa của cung) và $C$ là giao điểm thứ hai của đường thẳng $MD$ với đường tròn $O;R)$.
a. Giả sử $H$ là giao điểm của các đường thẳng $OM$ với $AB$. Chứng minh rằng $MH.MO = MC.MD$, từ đó suy ra đường tròn ngoại tiếp tam giác $HCD$ luôn đi qua một điểm cố định.
b. Chứng minh rằng nếu $AD$ song song với đường thẳng $MB$ thì đường thẳng $AC$ đi qua trọng tâm $G$ của tam giác $MAB$.
c. Kẻ đường kính $BK$ của đường tròn $(O;R)$, gọi $I$ là giao điểm của các đường thẳng $MK$ và $AB$. Tính bán kính đường tròn ngoại tiếp tam giác $MBI$ theo $R$, khi biết $OM = 2R$.
Bài 5. (2 điểm)
Cho các số thực dương $a, b, c$ thoả mãn: $abc + a + b = 3ab$. Chứng minh rằng:
$$\sqrt {\frac{{ab}}{{a + b + 1}}} + \sqrt {\frac{b}{{bc + c + 1}}} + \sqrt {\frac{a}{{ca + c + 1}}} \ge \sqrt 3 $$
-------------HẾT-------------
Bài viết đã được chỉnh sửa nội dung bởi xusinst: 23-03-2012 - 00:35