2 replies to this topic

[hxthanh]

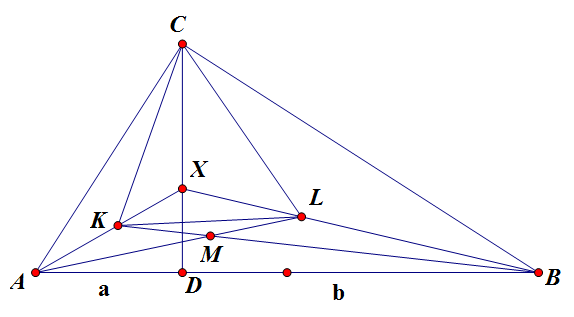
Bài toán 5. Cho tam giác vuông $ABC$ với $ \angle BCA = 90 ^ {\circ} $, $ D $ là chân đường cao hạ từ $ C $. $ X $ là một điểm trên đoạn $ CD $. $ K $ là điểm trên đoạn $AX $ sao cho $ BK = BC $. Tương tự, $ L $ là điểm trên đoạn $ BX $ sao cho $AL = AC $. $ AL $ và $ BK $ cắt nhau tại $M$.
Chứng minh rằng $MK = ML$

[perfectstrong]

Đã chém xong IMO Problem 5
Lời giải:
Đặt $DA=a;DB=b;DX=x;\dfrac{LX}{LB}=l;\dfrac{KX}{KA}=k$.
Dễ thấy
\[
DC=\sqrt{ab};AC^2 = a^2 + ab;BC^2 = b^2 + ab;AB = a + b\\
AX^2 - BX^2 = AD^2 - BD^2 = a^2 - b^2
\]

Ta có $L$ chia $XB$ theo tỉ số $-l$ nên
\[
\begin{array}{l}
\overrightarrow {LX} = - l\overrightarrow {LB} \Leftrightarrow \overrightarrow {LA} + \overrightarrow {AX} = - l\left( {\overrightarrow {LA} + \overrightarrow {AB} } \right) \\
\Leftrightarrow \left( {1 + l} \right)\overrightarrow {AL} = \overrightarrow {AX} + l\overrightarrow {AB} \\
\Rightarrow \left( {1 + l} \right)^2 AL^2 = \left( {\overrightarrow {AX} + l\overrightarrow {AB} } \right)^2 = AX^2 + l^2 AB^2 + 2l\overrightarrow {AX} .\overrightarrow {AB} \\
\Leftrightarrow \left( {1 + l} \right)^2 \left( {a^2 + ab} \right) = a^2 + x^2 + l^2 \left( {a + b} \right)^2 + l\left( {AX^2 + AB^2 - BX^2 } \right) \\
\Leftrightarrow \left( {a^2 + ab} \right)l^2 + 2\left( {a^2 + ab} \right)l + a^2 + ab=\\
= a^2 + x^2 + l^2 \left( {a + b} \right)^2 + l\left[ {a^2 - b^2 + \left( {a + b} \right)^2 } \right] \\
\Leftrightarrow \left( {b^2 + ab} \right)l^2 + x^2 = ab \Leftrightarrow l = \sqrt {\frac{{ab - x^2 }}{{b^2 + ab}}} = \frac{{\sqrt {ab - x^2 } }}{{BC}} \Leftrightarrow lBC = \sqrt {ab - x^2 } \\
\end{array}
\]
Tương tự, ta cũng có
\[
kAC = \sqrt {ab - x^2 }
\]
Chú ý $\dfrac{{BX}}{{BL}} = 1 + \dfrac{{LX}}{{LB}} = 1 + l$
Áp dụng định lý Menelaus cho $\vartriangle ALX$ với cát tuyến $KMB$, ta có
\[
\begin{array}{l}
\frac{{KX}}{{KA}}.\frac{{MA}}{{ML}}.\frac{{BL}}{{BX}} = 1 \Leftrightarrow \frac{{ML}}{{MA}} = \frac{{BL}}{{BX}}.\frac{{KX}}{{KA}} = \frac{k}{{l + 1}} \\
\Leftrightarrow \frac{{ML}}{{AL}} = \frac{k}{{l + k + 1}} \Leftrightarrow ML = \frac{{kAL}}{{l + k + 1}} = \frac{{kAC}}{{l + k + 1}} = \frac{{\sqrt {ab - x^2 } }}{{l + k + 1}}\left( 1 \right) \\
\end{array}
\]
Tương tự
\[
MK = \frac{{\sqrt {ab - x^2 } }}{{l + k + 1}}\left( 2 \right)
\]
Từ $(1),(2)$, ta có đpcm.

Edited by perfectstrong, 12-07-2012 - 22:42.

[perfectstrong]

Một lời giải khác bên Mathscope.org. Rất hay, dựa trên 1 bài toán cơ bản lớp 9

Hạ $BP\perp AX, AQ\perp BX$
Gọi $S$ là giao điểm của $AQ$ và $BP$.
Vì $X$ là trực tâm tam giác $SAB$ nên $SX\perp AB \Rightarrow S\in CD$.
Ta có $ AL^2=AC^2=AD.AB=AQ.AS\Rightarrow \widehat{ALS}=90^0$
$\Rightarrow SL^2=SQ.SA$
Tương tự $SK^2=SP.SB$
Từ đó $SL=SK$ mà $\widehat{MLS}=90^0=\widehat{MKS}=90^0$ nên $ML=MK$.

Edited by perfectstrong, 12-07-2012 - 22:51.