Nếu bạn muốn giảm thiểu tình trạng kẹt xe,việc xem xét loại bỏ một số tuyến đường là cần thiết. Không tin ư? Sau đây là một vài ví dụ:
Đầu tiên là việc đóng cửa tuyến đường số 42, tuyến đường nhộn nhịp nối liền hai phía của thành phố New York trong suốt ngày Trái đất vào tháng Tư năm 1990 đã được cảnh báo sẽ gây nên một cuộc khủng hoảng, Tuy nhiên, tờ The New York Times đưa tin vào ngày 25 – 12 – 1990 rằng lưu thông của xe cộ thực ra đã cải thiện.
Một ví dụ khác, vào năm 2003, dự án phục hồi dòng suối Cheonggyencheon bắt đầu tại Seoul đã loại bỏ 6 làn đường cao tốc. Dự án hoàn thành vào năm 2005, bên cạnh mang lại lợi ích đáng kể cho môi trường, các phương tiện giao thông đã di chuyển nhanh hơn, ta có thể quan sát điều này xung quanh thành phố.

Suối Cheonggyencheon
Tương tự, các nhà quy hoạch đã yêu cầu đóng một số phần đường Chính tại Boston và một số phần của đường nối Borough và các ga ngầm Farringdon ở London.
Nếu việc đóng các tuyến đường có khả năng giúp xe cộ di chuyển thuận lợi thì việc mở rộng các tuyến đường có những ảnh hưởng tiêu cực. Ví dụ, vào những năm cuối thập niên 60 của thế kỉ 19, thành phố Stuttgart đã quyết định mở thêm tuyến đường mới nhằm làm giảm áp lực giao thông ở trung tâm thành phố. Tuy nhiên, giao thông lại ngày một tắc nghẽn hơn và chính quyền phải đóng cửa tuyến đường này, làm cho giao thông trở nên ổn định hơn.
Những câu chuyện như thế này thì có rất nhiều và bạn chắc hẳn sẽ nghi ngờ, ẩn chứa đằng sau những vấn đề này chính là những vấn đề liên quan đến toán học. Thật vậy, vào năm 1968, nhà Toán học Dietrich Braess, khi đó đang làm việc tại viện nghiên cứu “Số học và Toán học ứng dụng” ở Münster, Đức, đã chứng minh rằng: “Việc mở rộng mạng lưới các tuyến đường bằng cách thêm một tuyến đường mới có thể phân bố lại lưu thông của các phương tiện giao thông, tức khiến thời gian đi lại sẽ tăng lên.” Ở bài toán này, Braess đã giả sử rằng người lái xe đều lái một cách ích kỷ, mỗi người sẽ tự chọn một tuyến đường mà họ thấy có lợi cho riêng bản thân họ, không cần phải chú ý đến lợi ích của người khác. Giả định này phản ánh điều kiện khắc nghiệt của giao thông vào giờ cao điểm khá tốt.
Hiện tượng do Braess tìm được bây giờ ta sẽ gọi là “nghịch lý Braess”, thực ra không hẳn là nghịch lý, hiện tượng này chỉ là những hành động không ngờ đến, cho thấy rằng chúng ta không được trang bị đủ tốt để dự đoán được kết quả của tập các tương tác.
Việc đóng cửa tuyến đường số 42 và dự án phục hồi dòng suối Cheonggyencheon chỉ là những ví dụ cho nghịch lý Braess khi những nơi loại bỏ một hay nhiều tuyến đường đã cải thiện thời gian đi lại trên cùng một mạng lưới đường bộ.

Những cây cột trụ còn lại sau khi phá bỏ đường cao tốc Cheonggyencheon
Bạn vẫn còn một chút ít nghi ngờ về nghịch lý Braess? Trong phần tiếp theo, chúng ta sẽ đi phân tích một ví dụ rất đơn giản.
I. TRƯỜNG HỢP VỚI MỘT CON ĐƯỜNG SIÊU NHANH
Mạng lưới đường đi từ $A$ đến $B$ như hình bên dưới:
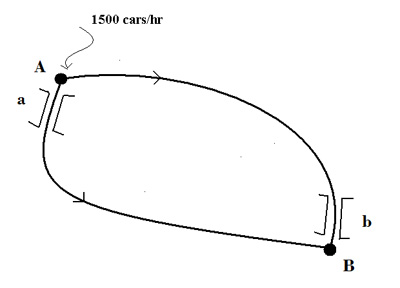
Mạng lưới đường đi
Vào giờ cao điểm, số lượng xe đi đến $A$ có thể lên đến 1500 xe trong một giờ, và các lái xe tự chọn cho mình một trong hai tuyến đường, tuyến 1 đi qua cây câu $a$, tuyến 2 đi qua cây cầu $b$.
Ta ký hiệu $L$ và $R$ để biểu thị cho số xe đi đến $B$ trong một giờ lần lượt qua tuyến đường 1 và tuyến đường 2.
Các cây cầu $a$ và $b$ là nơi gây tắt nghẽn giao thông. Chúng ta sẽ giả sử rằng thời gian qua cả hai cây cầu tỉ lệ thuận với số lượng xe đi qua trong mỗi giờ. Cụ thể, chúng ta giả sử rằng thời gian di chuyển qua cây cầu $a$ là $\frac{L}{100}$ phút và cây cầu $b$ là $\frac{R}{100}$ phút. Phần còn lại của hai tuyến đường là một trục đường giao thông khá lớn với thời gian di chuyển là 20 phút. Phải nói rằng, mặc dù giả định này có ý nghĩa, việc tính toán cho một mạng lưới trong thực tế là một ví dụ khó khi mô hình toán học.
Chúng ta muốn biết phân bố giao thông dự kiến, tức số lượng xe trên một giờ hay trên mỗi tuyến đường. Để làm được như thế, chúng ta tưởng tượng rằng mỗi tài xế đều lái xe đi qua mạng lưới nhiều lần, cụ thể là trường hợp cho tài xế lái xe mỗi ngày vào giờ cao điểm, điều này đã giúp ta phát triển một chiến lược đăc biệt giúp giảm thiểu thời gian đi lại. Theo như giả sử này, thời gian đi lại phải giống nhau với tất cả các tài xế lái xe, nếu không sẽ có một vài tác động để các tài xế lái xe thay đổi chiến lược di chuyển của mình. Ta gọi đây là trạng thái ổn định, hay cân bằng Nash, được đặt theo tên của nhà toán học đã giành giải Nobel là John F.Nash. Một trong những đóng góp của Nash có tên gọi là “trò chơi không hợp tác”, trong đó giao thông vào giờ cao điểm là một ví dụ cho trò chơi này.

John Nash, tháng 3, 2008
Lưu ý rằng cân bằng Nash khác với tính cân bằng của cốc trà trên mặt bàn. Có thể nói rằng trong trường hợp này, cân bằng Nash là một cân bằng động nhằm duy trì lượng xe cần thiết đi vào $A$ mỗi giờ. Trạng thái cân bằng là tất cả mọi người đều có thời gian đi lại như nhau, không có ai hơn ai cả mặc dù chúng ta đã giả sử rằng tất cả các tài xế lái xe đều hành động ích kỉ, cố gắng giảm thời gian đi lại của họ và không quan tâm đến lợi ích của người khác. Nói cách khác, cho dù họ muốn hay không thì mỗi tài xế vẫn chịu tác động ảnh hưởng bởi những quyết định của các tài xế khác.
Bây giờ, ta xét thời gian đi lại (tính theo phút) trên mỗi tuyến đường:
$$\begin{array}{|c|c|} \hline \text{Đường 1:} & \frac{L}{100}+20 \\ \hline \text{Đường 2:} & \frac{R}{100}+20 \\ \hline \end{array}$$
Ở trạng thái cân bằng, chúng ta có thể viết:
$$\frac{L}{100}+20=\frac{R}{100}+20$$
Hơn nữa, số lượng dòng xe lưu thông phải là tổng các xe $L$ và $R$, vậy:
$$L+R=1500$$
Giải đồng thời hai phương trình trên, ta tìm được:
$$L=R=750$$
Như vậy, phân bố giao thông đồng đều ở cả hai tuyến đường với thời gian đi lại là 27,5 phút.
Bây giờ chúng ta giả định rằng hệ thống đường bộ mở rộng thêm và phát triển một tuyến đường $c$ mới, đi siêu nhanh chỉ với 7 phút.
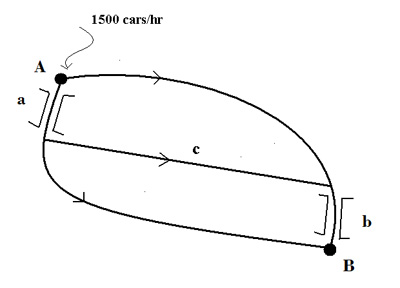
Mở rộng mạng lưới đường đi
Liệu tuyến đường mới thêm vào hệ thống này có giảm thời gian di chuyển không? Cùng xem nhé!
Các tài xế lái xe bây giờ có thể chọn một trong 3 con đường, gồm 2 tuyến đường đã nêu ở trên và một tuyến đường thứ 3 là tuyến đường đi qua cây cầu $a$, đi theo đường $c$ và cuối cùng là đi qua cây cầu $b$. Như ở trên, ta gọi $L$ là lưu lượng xe ô tô đến $B$ qua tuyến đường 1, $R$ là lưu lượng xe rời $A$ theo tuyến đường 2. Ngoài ra, ta ký hiệu $C$ là lưu lượng xe đi trên tuyến đường $c$. Do đó, số lượng xe mỗi giờ đi qua cây cầu $a$ là $L+C$, số lượng xe mỗi giờ đi qua cây cầu $b$ là $R+C$. Do đó, thời gian đi lại trên 3 tuyến đường sẽ là:
Một lần nữa, chúng ta muốn tìm sự phân bố giao thông trên 3 tuyến đường.
Như đã đề cập ở trên, giao thông sẽ đạt đến một trạng thái ổn định hay cân bằng Nash khi thời gian đi lại là như nhau đối với tất cả các tài xế lái xe. Do vậy, ở trạng tháng cân bằng, chúng ta có:
$$\frac{L+C}{100}+20=\frac{R+C}{100}+20=\frac{L+C}{100}+7+\frac{R+C}{100}$$
Từ đó cho ta hai phương trình sau:
$$\frac{L+C}{100}+20=\frac{R+C}{100}+20$$
$$\frac{R+C}{100}+20~=\frac{\left( L+C \right)}{100}+7+\frac{R+C}{100}$$
Ngoài ra, ta còn có:
$$R+L+C=1500$$
Từ 3 phương trình trên, ta xác định được $L$, $R,$ $C$ và thời gian đi lại chung cho tất cả các lái xe:
$$L=R=200$$
$$C~=1100$$
$$\text{Thời gian di chuyển }=33\text{ phút}$$
Điều này cho thấy thời gian di chuyển là 33 phút, tăng 20% so với thời gian trước khi mở tuyến đường $c$.
Có gì không ổn ở đây! Con đường siêu nhanh này đã dụ được nhiều tài xế lái xe, gây ra tình trạng tắc nghẽn và ảnh hưởng xấu đến toàn bộ hệ thống đường bộ ở đây. Không có một tài xế nào có động cơ để chuyển sang một tuyến đường khác vì tất cả họ đều có cùng thời gian đi lại, do đó tất cả họ sẽ bị kẹt lại. Nói cách khác, hành vi ích kỷ của họ đã làm cho mạng lưới đường bộ mới mất đi hiệu quả, tăng thời gian đi lại lên đến 20% trước khi mở tuyến đường mới. Các nhà kinh tế học gọi hiện tượng này là “Giá phải trả cho tình trạng hỗn loạn”. Tuy nhiên, nếu các tài xế lái xe chấp nhận không đi con đường $c$, thì thời gian di chuyển sẽ giảm. Lựa chọn này giống như áp dụng chiến lược hợp tác xã, trong đó các lái xe thống nhất với nhau về việc chọn tuyến đường sẽ đi. Thực tế, có một số mạng lưới đường đi có bảng chỉ dẫn giao thông, khi đó sẽ không xảy ra nghịch lý Braess, nghịch lý này chỉ đúng khi các lái xe tự chọn tuyến đường tốt nhất cho mình.
II. NGHỊCH LÝ BRAESS LÀ MỘT NGHỊCH LÝ PHỨC TẠP
Ta dễ dàng nhận thấy rằng nếu lưu lượng xe đủ nhỏ thì nghịch lý Braess sẽ không xảy ra. Nhưng trên thực tế, ta quan sát được rằng các tài xế lái xe luôn hành động ích kỷ, họ đã thay đổi tuyến đường ban đầu của họ để tìm đến tuyến đường siêu nhanh nhưng vẫn không làm cho thời gian di chuyển của họ ngắn lại.
Mặt khác, người ta nghĩ rằng sự tăng lên nhanh chóng của lưu lượng xe sẽ làm cho mọi thứ trở nên tồi tệ. Tuy nhiên, điều này không phải lúc nào cũng đúng. Trong ví dụ chúng ta xét ở trên, các nhà khoa học đã đoán rằng khi nhu cầu lưu thông tăng cao sẽ xuất hiện hiệu ứng “trí tuệ đám đông” khi con đường mới sẽ không được tin dùng. Thực vậy, những quyết định cá nhân trong một nhóm đủ nhiều các tài xế sẽ tối ưu hóa thời gian đi lại cho tất cả mọi người. Giả thuyết này đã được chứng minh bởi nhà toán học Anna Nagurney, giáo sư của trường Isenberg thuộc Đại học Massachusetts.
III. TRƯỚC KHI KẾT THÚC…
Nghịch lý Braess xuất hiện trong nhiều trường hợp. Ví dụ, bài viết If we all go for the blonde (tạm dịch: Nếu tất chúng ta đều gặp cô gái tóc hoe, xem tại https://plus.maths.o...e-all-go-blonde) có nhân vật là cô gái tóc hoe được cho là có sức quyến rũ lớn khiến nhiều chàng trai yêu thích (giống như nhiều tài xế thích con đường siêu nhanh), từ đó xuất hiện hiệu ứng tương tự, một trường đông nghịch. Nhưng nếu ta tiếp tục sử dụng mạng lưới này, ta có thể quan sát nghịch lý với dữ liệu di chuyển trong mạng lưới máy tính và công suất sử dụng trong hệ thống đường dây. Hơn thế nữa, vào năm 2012, một nhóm nghiên cứu quốc tế đã chứng minh về mặt lý thuyết cũng như trên thực tế, nghịch lý Braess có thể được sử dụng trong các hệ thống điện tử.
Ví dụ về hệ thống đường bộ mở rộng cho thấy rằng ở trạng thái cân bằng, phân bố xe trong hệ thống mạng lưới không cần phải tối ưu. Điều này đưa chúng ta đến một khái niệm thú vị, được phát triển bởi nhà kinh tế học Vilfredo Pareto (1848-1923). Pareto đã tuyên bố rằng, phân bố các nguồn lực được gọi là tối ưu nếu như không một cá nhân nào có cuộc sống tốt lên mà không khiến ít nhất một người khác có cuộc sống xấu đi. Một phân bố như thế được gọi là tối ưu Pareto.

Đi đâu đây?
Trong ví dụ, các tuyến đường trong hệ thống là các nguồn tài nguyên. Việc bỏ qua những con đường mới này làm cho mọi người tốt hơn, như làm giảm thời gian di chuyển. Do đó, sự cân bằng trong mạng lưới mở rộng là một ví dụ về cân bằng Nash mà không phải là tối ưu Pareto.
Cuối cùng, ta mô tả phân bố tài nguyên như tối ưu Pareto không cần có sự công bằng theo ý nghĩa xã hội. Ví dụ ,việc sử dụng tài nguyên mà tôi chiếm lĩnh trong khi người khác lại không có gì là một tối ưu Pareto bởi vì cách duy nhất để cải thiện đời sống của họ là tôi phải mất đi một vài thứ nào đó. Những nỗ lực do các nhà kinh tế học, trong đó có Ravi Kanbur của đại học Cornell, thực hiện nhằm tái cấu trúc khái niệm tối ưu Pareto, thêm một cách tính định lượng để đo sự cân bằng.
Nguồn: https://plus.maths.o...ild-fewer-roads
Người dịch: Phan Thành Nhân, thành viên Chuyên san EXP







