Một số bài toán đầu tiên :
$1.$ Cho đường tròn $(O;R)$ có dây cung cố định, $AB=R\sqrt{3}$. Điểm $P$ di động trên dây $AB$ ($P$ khác $A,B$). Gọi $(I;R_{1})$ là đường tròn qua $P$ và tiếp xúc với đường tròn $(O)$ tại $A$; $(k;R_{2})$ là đường tròn qua $P$ và tiếp xúc với đường tròn $(O)$ tại $B$. Hai đường tròn $(I)$ và $(K)$ còn cắt nhau tại điểm $M$ ($M$ khác $P$).
$a)$ Chứng minh $R=R_{1}+R_{2}$ và tứ giác $MIKO$ nội tiếp
$b)$ Chứng minh $M$ di động trên một đường cố định
$c)$ Chứng minh đường thẳng $MP$ luôn đi qua một điểm cố định $N$. Xác định vị trí của $P$ trên $AB$ sao cho $PM.PN$ đạt GTLN.
$2.$ Cho tam giác $ABC$ có ba góc nhọn nội tiếp đường tròn $(O)$. $B,C$ cố định, $D,E$ lần lượt là các điểm chính giữa của các cung nhỏ $AB,AC$. $DE$ cắt $AB,AC$ lần lượt tại $H,K$.
$a)$ Chứng minh tam giác $AHK$ là tam giác cân
$b)$ Gọi $I$ là giao điểm của $BE$ và $CD$. Chứng minh rằng đường thẳng $AI$ luôn đi qua một điểm cố định khi $A$ lưu động trên cung $BC$
$c)$ Chứng minh rằng tỉ số $\frac{AH}{HK}$ không phụ thuộc vào vị trí của điểm $A$.
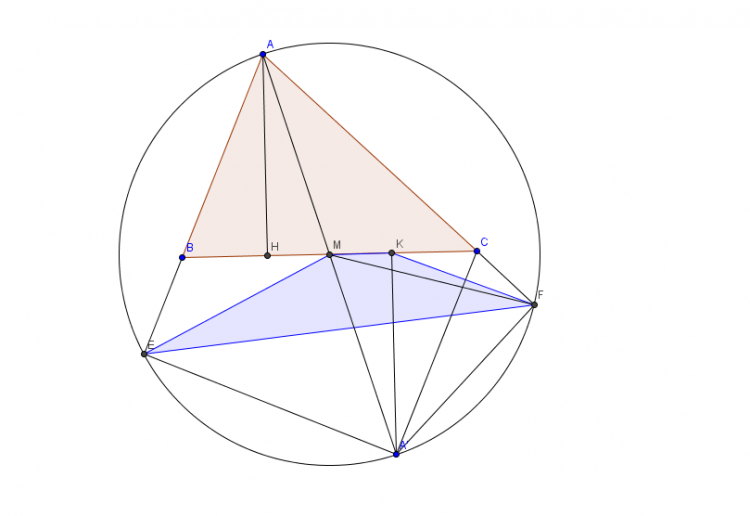
$3.$ Cho $\Delta ABC$ có $A<90^{\circ}$, đường cao $AH$ và trung tuyến $AM$. Trên tia $AB$ và $AC$ theo thứ tự lấy điểm $E$ và $F$ sao cho $ME=MF=MA$. Gọi $K$ là điểm đối xứng của $H$ qua $M$. Chứng minh rằng tứ giác $EMKF$ nội tiếp đường tròn.
$4.$ Cho $\Delta ABC$ ngoại tiếp đường tròn $(O)$, gọi $D$ là tiếp điểm của $BC$ với đường tròn. Gọi $(O')$ là đường tròn bàng tiếp trong góc $A$ của $\Delta ABC$ và tiếp xúc với $BC$ tại $F$. Vẽ đường kính $DE$ của đường tròn $(O)$. Chứng minh rằng $A,E,F$ thẳng hàng.
$5.$ Cho $\Delta ABC$ có 3 góc nhọn. Từ điểm $I$ thuộc miền trong của $\Delta ABC$, vẽ $IH\perp BC, IK\perp CA, IL\perp AB(H\in BC, K\in CA, L\in AB)$. Xác định vị trí của điểm $I$ sao cho $AL^{2}+BH^{2}+CK^{2}$ nhỏ nhất.
$6.$ Cho $\Delta ABC$ có các góc đều nhọn. Trên cung nhỏ $BC$ của đường tròn ngoại tiếp tam giác ta lấy một điểm $D$. Gọi $A',B',C'$ lần lượt là hình chiếu vuông góc của $D$ trên $BC,CA,AB$. Chứng minh rằng: $\frac{BC}{DA'}=\frac{CA}{DB'}+\frac{AB}{DC'}$
$7.$ Cho tam giác đều $ABC$. Gọi $D$ là điểm đối xứng của $B$ qua đường thẳng $AC$. Đường thẳng qua $B$ cắt các đường thẳng $AD,CD$ lần lượt tại $M,N$. Các đường thẳng $AN,CM$ cắt nhau tại điểm $E$. Chứng minh bốn điểm $A,C,D,E$ cùng nằm trên một đường tròn.
$8.$ Cho tam giác đều $ABC$ có cạnh $AB=a$. Một đường thẳng đi qua trọng tâm $G$ của tam giác cắt các đường thẳng $BC,CA,AB$ lần lượt tại $M,N,P$. Chứng minh rằng: $\frac{1}{GM^{4}}+\frac{1}{GN^{4}}+\frac{1}{GP^{4}}$ là không đổi.
p/s: Mong các bạn đóng góp nhiều bài hay hơn nữa cho topic của mình
Bài viết đã được chỉnh sửa nội dung bởi ngobaochau1704: 08-02-2016 - 20:04