Chủ đề này có 63 trả lời

[tpdtthltvp]

 

Đề số 5

 

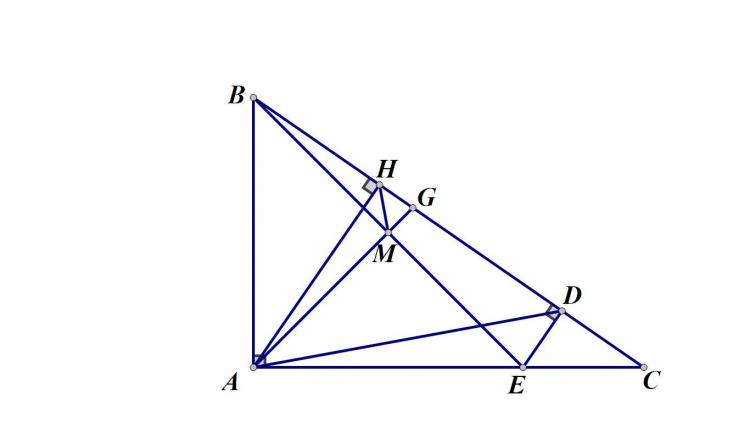
Câu 4: Cho tam giác $ABC$ vuông tại $A$ ($AC>AB$), đường cao $AH$ ($H \in BC$). Trên tia $HC$ lấy điểm $D$ sao cho $HD=HA$. Đường vuông góc với $BC$ tại $D$ cắt $AC$ tại $E$.

a, CMR: $\Delta BEC$ đồng dạng với $\Delta ADC$. Tính độ dài $BE$ theo $m=AB$

b, Gọi $M$ là trung điểm đoạn $BE$. CMR: hai tam giác BHM và BEC đồng dạng. Tính số đo $\widehat{AHM}$

c, Tia $AM$ cắt $BC$ tại $G$. CM: $\dfrac{GB}{BC}=\dfrac{HD}{AH+HC}$

 

 

Câu 4:

a, Ta có: $\Delta DEC\sim \Delta ABC(g-g)\Rightarrow \frac{DC}{AC}=\frac{EC}{BC}\Rightarrow \frac{BC}{AC}=\frac{EC}{CD}$

$\Rightarrow \Delta BEC\sim \Delta ADC(c-g-c)$

$\Rightarrow \widehat{BEC}=\widehat{ADC}\Rightarrow \widehat{AEB}=\widehat{ADB}=45^o\Rightarrow \Delta ABE$ vuông cân tại $A$

$\Rightarrow BE^2=AB^2+AE^2=2AB^2=2m^2\Rightarrow BC=\sqrt{2m^2}$

b,

$\Delta HBA\sim \Delta ABC(g-g)\Rightarrow BH.BC=AB^2$

mà $AB^2=BM^2+MA^2=2BM^2=BM.BE$

$\Rightarrow BH.BC=BM.BE\Rightarrow \frac{BH}{BE}=\frac{BM}{BC}\Rightarrow \Delta BHM\sim \Delta BEC(c-g-c)$

$\Rightarrow \widehat{BHM}=\widehat{BEC}=180^o-\widehat{AEB}=135^o\Rightarrow \widehat{AHM}=\widehat{BHM}-90^o=45^o$

c,

$\frac{GB}{BC}=\frac{HD}{AH+HC}\Leftrightarrow \frac{GB}{GB+GC}=\frac{AH}{AH+HC}\Leftrightarrow \frac{GB}{GC}=\frac{AH}{HC}(*)$

Mà $\Delta ABE$ vuông cận tại $A$ có $AM$ là trung tuyến $\Rightarrow AM$ là phân giác của $\widehat{BAC}$

$\Rightarrow \frac{GB}{GC}=\frac{AB}{AC}$ mà $\Delta ABC\sim \Delta AHC\Rightarrow \frac{AB}{AC}=\frac{AH}{HC}\Rightarrow \frac{GB}{GC}=\frac{AH}{HC}(**)$

Từ $(*),(**)$ suy ra đpcm.

Bài viết đã được chỉnh sửa nội dung bởi tpdtthltvp: 21-03-2016 - 20:02

[dunghoiten]

 

Đề số 5

 

Bài 5

 

b, Tìm GTNN và GTLN của biểu thức $B=x+y+z$. Biết rằng $x,y,z$ là các số thực thỏa mãn điều kiện $y^2+yz+z^2=1007-\dfrac{3x^2}{2}$

 

 

 

 

$y^2+yz+z^2=1007-\dfrac{3x}{2} \leftrightarrow 2y^2+2yz+2z^2+3x^2=2014$

 

$\leftrightarrow x^2+y^2+z^2+(x^2+y^2)+(x^2+z^2)+2yz=2014$

 

$\geqslant x^2+y^2+z^2+2xy+2xz+2yz=(x+y+z)^2$

 

$\rightarrow (x+y+z)^2 \leqslant 2014$

 

$\rightarrow -\sqrt{2014} \leqslant x+y+z \leqslant \sqrt{2014}$

 

Vậy $Min_B=-\sqrt{2014} \leftrightarrow x=y=z=\dfrac{-\sqrt{2014}}{3}$

 

       $Max_B=\sqrt{2014} \leftrightarrow x=y=z=\dfrac{\sqrt{2014}}{3}$

Bài viết đã được chỉnh sửa nội dung bởi dunghoiten: 21-03-2016 - 20:06

[Trung Kenneth]

                                                                          ĐỀ THI SỐ 4 

 

Câu 7: Tìm tất cả các số nguyên dương  $a$ để $a^4+a^3+1$ là một số chính phương.

 

Vì $a\in N ^{*}$ $\Rightarrow a^4+a^3+1> (a^2)^2$

Vì $a^4+a^3+1$ là số chính phương nên đặt $a^4+a^3+1=(a^2+k)^2$ ($k\in N^{*}$)

$\Rightarrow a^3-2a^2k=k^2-1\Rightarrow a^2(a-2k)=k^2-1$ (1)

Từ (1) $\Rightarrow k^2-1\vdots a^2$

Mà $k^2-1\geq 0$ nên $k^2-1=0$ hoặc $k^2-1\geq a^2$

 Với $k^2=1\Rightarrow k=1(k\in N^{*})$

 Thay vào được a=2 thỏa mãn

 Với $k^2-1\geq a^2$ và $k^2-1< k^2$

nên $a^2 < k^2$ suy ra $a<k$ mà $a,k\in N^{*}$ nên $a< 2k$$\Rightarrow a-2k<0$

mâu thuẫn với (1) vì $a^2(a-2k)< 0$ mà $k^2-1\geq 0$

Vậy a=2

Bài viết đã được chỉnh sửa nội dung bởi Trung Kenneth: 21-03-2016 - 20:38

[NTA1907]

Đề số 6

Bài 1:

1, Phân tích thành nhân tử: $x^{2}-2x-4y^{2}-4y$

2, Cho $a\neq 0,b\neq 0,c\neq 0$ và $a+b+c=0$. Tính giá trị của biểu thức: 

$A=\frac{a^{2}}{a^{2}-b^{2}-c^{2}}+\frac{b^{2}}{b^{2}-c^{2}-a^{2}}+\frac{c^{2}}{c^{2}-a^{2}-b^{2}}$

Bài 2:

1, Giải phương trình: $2x(8x-1)^{2}(4x-1)=9$

2, Tìm x,y,z thoả mãn điều kiện: $\left\{\begin{matrix} &x+y=2 \\ &xy-z^{2}=1 \end{matrix}\right.$

Bài 3:

1, Cho a,b,c là độ dài 3 cạnh của tam giác có chu vi bằng 2. CMR: $a^{2}+b^{2}+c^{2}+2abc< 2$

2, Tìm GTLN của biểu thức: $P=2-5x^{2}-y^{2}-4xy+2x$

Bài 4: Cho tứ giác $ABCD$ có trung điểm 2 đường chéo $M,N$ không trùng nhau. Đường thẳng $MN$ cắt $AD$ ở $P$ và $BC$ ở $Q$. Chứng minh: $\frac{PA}{PD}=\frac{QC}{QB}$

Bài 5: Cho hình thang $ABCD(AB//CD)$. Gọi $E,F$ lần lượt là trung điểm của $BD$ và $AC$. Gọi $G$ là giao điểm của đường thẳng đi qua $E$ vuông góc với $AD$ với đường thẳng đi qua $F$ vuông góc với $BC$. So sánh $GC$ và $GD$

 

--------------------Hết--------------------

Bài viết đã được chỉnh sửa nội dung bởi tpdtthltvp: 21-03-2016 - 21:24

[I Love MC]

 

 

Đề số 6

Bài 3:

1, Cho a,b,c là độ dài 3 cạnh của tam giác có chu vi bằng 2. CMR: $a^{2}+b^{2}+c^{2}+2abc< 2$

 

Sao lại ẩn đề của  mình đi nhỉ  
Câu 3/1: $a+b+c=2>a+a=2a \Rightarrow 1>a$ . Tương tự $1>b,c$ 
$\Rightarrow (1-a)(1-b)(1-c)>0 \Leftrightarrow abc<ab+bc+ac-1 \Leftrightarrow a^2+b^2+c^2+2abc<2ab+2ac+2bc+a^2+b^2+c^2-2=2$ 
Mở rộng $\frac{52}{27} \le \sum a^2+2abc <2$

Bài viết đã được chỉnh sửa nội dung bởi tpdtthltvp: 21-03-2016 - 21:38

[tpdtthltvp]

 

Đề số 6

Bài 1:

1, Phân tích thành nhân tử: $x^{2}-2x-4y^{2}-4y$

2, Cho $a\neq 0,b\neq 0,c\neq 0$ và $a+b+c=0$. Tính giá trị của biểu thức: 

$A=\frac{a^{2}}{a^{2}-b^{2}-c^{2}}+\frac{b^{2}}{b^{2}-c^{2}-a^{2}}+\frac{c^{2}}{c^{2}-a^{2}-b^{2}}$

Bài 2:

1, Giải phương trình: $2x(8x-1)^{2}(4x-1)=9$

 

Bài 1:

1. $x^2-2x-4y^2-4y=x(x-2y-2)+2y(x-2y-2)=(x+2y)(x-2y-2)$

2. $a+b+c=0\Rightarrow a^2=(b+c)^2\Rightarrow a^2-b^2-c^2=2bc$

Tượng tự, suy ra:

$$\sum \frac{a^2}{a^2-b^2-c^2}=\sum \frac{a^2}{2bc}=\frac{a^3+b^3+c^3}{2abc}=\frac{3abc}{2abc}=\frac{3}{2}$$

 

Bài 2:

1, $2x(8x-1)^{2}(4x-1)=9$

$\Leftrightarrow (64x^2-16x+1)(8x^2-2x)=9$

$\Leftrightarrow (64x^2-16x+1)(84x^2-16x)=72$

Đặt $64x^2-16x=a$ thì:

$(a+1)a=72\Leftrightarrow (a-8)(a+9)=0\Leftrightarrow \begin{bmatrix} a=8 \\ a=-9 \end{bmatrix}\Rightarrow \begin{bmatrix} 64x^2-16x=8 \\ 64x^2-16x=-9 \end{bmatrix}\Rightarrow \begin{bmatrix} x=-\frac{1}{4} \\ x=\frac{1}{2} \end{bmatrix}$

[tpdtthltvp]

 

Đề số 6

Bài 2:

2, Tìm x,y,z thoả mãn điều kiện: $\left\{\begin{matrix} &x+y=2(1) \\ &xy-z^{2}=1(2) \end{matrix}\right.$

Bài 3:

2, Tìm GTLN của biểu thức: $P=2-5x^{2}-y^{2}-4xy+2x$

 

Bài 2/2:

Từ PT (1) $\Rightarrow y=2-x$

$\Rightarrow x(2-x)=1+z^2\Rightarrow 1+z^2+x^2-2x=0\Rightarrow (x-1)^2+z^2=0\Rightarrow \left\{\begin{matrix} x=1 \\ z=0 \end{matrix}\right.\Rightarrow y=1$

Vậy $(x;y;z)=(1;1;0)$

 

Bài 3/2:

$P=2-5x^{2}-y^{2}-4xy+2x=3-(4x^2+4xy+y^2)-(x^2-2x+1)=3-(2x+y)^2-(x-1)^2\leq 3$

Vậy $GTLN_P=3\Leftrightarrow \left\{\begin{matrix} x=1 \\ y=-2 \end{matrix}\right.$

[NTA1907]

 

Đề số 6

Bài 4: Cho tứ giác $ABCD$ có trung điểm 2 đường chéo $M,N$ không trùng nhau. Đường thẳng $MN$ cắt $AD$ ở $P$ và $BC$ ở $Q$. Chứng minh: $\frac{PA}{PD}=\frac{QC}{QB}$

Từ $B$ và $D$ kẻ các đương thẳng song song với $AC$ cắt đường $MN$ lần lượt ở $E$ và $F$.

$\Delta BQE\sim \Delta CQN$(g.g) 

$\Rightarrow \frac{QC}{QB}=\frac{CN}{BE}$(1)

$\Delta PDF\sim \Delta PAN$(g.g)

$\Rightarrow \frac{PA}{PD}=\frac{AN}{DF}$(2)

Mà ta có: $\Delta MDF=\Delta MBE(g.c.g)\Rightarrow BE=DF$(3)

Từ (1),(2) và (3)$\Rightarrow$ đpcm

Bài viết đã được chỉnh sửa nội dung bởi tpdtthltvp: 23-03-2016 - 07:03

[NTA1907]

 

Đề số 6

Bài 5: Cho hình thang $ABCD(AB//CD)$. Gọi $E,F$ lần lượt là trung điểm của $BD$ và $AC$. Gọi $G$ là giao điểm của đường thẳng đi qua $E$ vuông góc với $AD$ với đường thẳng đi qua $F$ vuông góc với $BC$. So sánh $GC$ và $GD$

Gọi $K$ là giao điểm của $GE$ với $AD$, $H$ là giao điểm của $GF$ với $BC$, $I$ là trung điểm $CD$

Ta thấy $IE$ là đường trung bình của $\Delta BDC\Rightarrow IE//BC$

Mà $GH$ vuông góc với $BC\Rightarrow GH$ vuông góc với $IE$

Tương tự$\Rightarrow GK$ vuông góc với $IF$

$\Rightarrow G$ là trực tâm $\Delta EIF\Rightarrow IG$ vuông góc với $EF$

Mà $EF//CD$ nên $IG$ vuông góc với $CD\Rightarrow GC=GD$

Bài viết đã được chỉnh sửa nội dung bởi tpdtthltvp: 23-03-2016 - 07:18

[I Love MC]

                                                                                        ĐỀ THI SỐ 6  
Bài 1 :

      a) Cho $y$ là tham số . Chứng minh rằng phương trình sau luôn có nghiệm $x^2-y^2+x-3y-2=0$ 
      b) Tìm số nguyên $a$ sao cho đa thức $(x+a)(x-5)+2$ phân tích được thành $(x+b)(x+c)$ ($b,c \in \mathbb{Z}$ 
Bài 2:

      a) Chứng minh rằng với mọi $t$ thì ta đều có $t^4-t+\frac{1}{2}>0$ 
      b) Cho $a,b,c$ là ba số thực khác nhau . Chứng minh rằng : $\sum \frac{a+b}{a-b}.\frac{b+c}{b-c}=-1$ 
      c) Cho $a,b,c$ là $3$ số nguyên khác $0$ thỏa $\frac{a}{b}+\frac{b}{c}+\frac{c}{a}=3$. Chứng minh tích $abc$ là lập phương của một số nguyên.
Bài 3:

      a) Giải phương trình $x^2(x^4-1)(x^2+2)+1=0$ 
      b) Một cậu bé rất mê sưu tập ảnh thẻ  dự định trung bình mỗi ngày cậu sưu tập $30$ cái thẻ . Nhưng thực tế vì cậu ngoan ngoãn nên mỗi ngày đã sưu tập thêm được $8$ cái thẻ, nên chẳng những đã hoàn thành kế hoạch sớm hơn $2$ ngày mà còn sưu tập vượt mức $20$ cái thẻ. Hỏi số thẻ dự định sưu tập của cậu là bao nhiêu ? 
Bài 4:

      a)  Cho tam giác $ABC$ với $\widehat{ABC}=\widehat{ACB}=50^{o}$. $N$ là điểm thuộc miền trong của tam giác thỏa mãn $\widehat{NBC}=10^{o},\widehat{NCB}=20^{o}$. Tính góc $ANB$ 
      b) Cho hình vuông $ABCD$ có cạnh bằng $1$. $M$ là điểm bất kì nằm trong hình vuông. Chứng minh $MA^2+MB^2+MC^2+MD^2 \ge 2$
Bài 5: Tìm giá trị nhỏ nhất của biểu thức $A$ biết rằng $a,b,c>0$ và $abc=1$. Và 
$A=\frac{a^2(b+c)}{b\sqrt{b}+c\sqrt{c}}+\frac{b^2(c+a)}{c\sqrt{c}+a\sqrt{a}}+\frac{c^2(a+b)}{a\sqrt{a}+b\sqrt{b}}$

Bài 6:

      a) Tìm nghiệm nguyên dương của phương trình sau  : 
$8(\sqrt[3]{\frac{x^3-3x+(x^2-1)\sqrt{x^2-4}}{2}}+\sqrt[3]{\frac{x^3-3x-(x^2-1)\sqrt{x^2-4}}{2}})=y^2-z^2+16$ . Trong đó $2 \le y <x<10$  

      b) Chứng minh rằng với mỗi số tự nhiên $n$, giữa $n^2$ và $(n+1)^2$ có thể tìm được ba số tự nhiên $a,b,c$ sao cho $c|(a^2+b^2)$

Bài viết đã được chỉnh sửa nội dung bởi tpdtthltvp: 23-03-2016 - 18:34

[tpdtthltvp]

                                                                                        ĐỀ THI SỐ 6  
Bài 1 :

      a) Cho $y$ là tham số . Chứng minh rằng phương trình sau luôn có nghiệm $x^2-y^2+x-3y-2=0$ 
      b) Tìm số nguyên $a$ sao cho đa thức $(x+a)(x-5)+2$ phân tích được thành $(x+b)(x+c)$ ($b,c \in \mathbb{Z}$ 
Bài 2:

      b) Cho $a,b,c$ là ba số thực khác nhau . Chứng minh rằng : $\sum \frac{a+b}{a-b}.\frac{b+c}{b-c}=-1$ 

Bài 3:

      b) Một cậu bé rất mê sưu tập ảnh thẻ  dự định trung bình mỗi ngày cậu sưu tập $30$ cái thẻ . Nhưng thực tế vì cậu ngoan ngoãn nên mỗi ngày đã sưu tập thêm được $8$ cái thẻ, nên chẳng những đã hoàn thành kế hoạch sớm hơn $2$ ngày mà còn sưu tập vượt mức $20$ cái thẻ. Hỏi số thẻ dự định sưu tập của cậu là bao nhiêu ? 
 

Bài 1:

a) $x^2-y^2+x-3y-2=0\Leftrightarrow x^2+x-(y^2+3y+2)=0$

Ta có: $\Delta _x=1+4(y^2+3y+2)=4y^2+12y+9=(2y+3)^2\geq 0$ với mọi $y$.

Vậy PT luôn có nghiệm.

b) Ta có:

$(x+a)(x-5)+2=(x+b)(x+c)\Leftrightarrow x^2+(a-5)x+(-5a+2)=x^2+(b+c)x+bc$

Đồng nhất các hệ số $\Rightarrow \left\{\begin{matrix} a-5=b+c \\ -5a+2=bc \end{matrix}\right.\Rightarrow \left\{\begin{matrix} a=b+c+5 \\ a=-\frac{bc-2}{5} \end{matrix}\right.$

$\Rightarrow b+c+5=-\frac{bc-2}{5}\Leftrightarrow 5b+5c+bc+23=0\Leftrightarrow (b+5)(c+5)=2=1.2=(-2).(-1)$

Giả sử $b\leq c\Rightarrow b+5\leq c+5$. Xét các TH:

$\bullet \left\{\begin{matrix} b+5=1 \\ c+5=2 \end{matrix}\right.\Rightarrow \left\{\begin{matrix} b=-4 \\ c=-3 \end{matrix}\right.\Rightarrow a=-2(t/m)$

$\bullet \left\{\begin{matrix} b+5=-2 \\ c+5=-1 \end{matrix}\right.\Rightarrow \left\{\begin{matrix} b=-7 \\ c=-6 \end{matrix}\right.\Rightarrow a=-6(t/m)$

Vậy $a\in \left \{ -2;-6 \right \}$

 

Bài 2:

b) Đặt $\frac{a+b}{a-b}=a;\frac{b+c}{b-c}=b;\frac{c+a}{c-a}=c\Rightarrow (a+1)(b+1)(c+1)=(a-1)(b-1)(c-1)\Rightarrow ab+bc+ca=-1$

Vậy $\sum \frac{a+b}{a-b}.\frac{b+c}{b-c}=-1$

 

Bài 3:

b) Gọi số ngày dự định là $x$. Ta có PT:

$30x=38(x-2)+20\Leftrightarrow x=7$

Vậy số thẻ dự định sưu tập là $30.7=210$. (thẻ)

Bài viết đã được chỉnh sửa nội dung bởi tpdtthltvp: 23-03-2016 - 19:26

[thanhmylam]

                                                                                        ĐỀ THI SỐ 6  

Bài 2:

      a) Chứng minh rằng với mọi $t$ thì ta đều có $t^4-t+\frac{1}{2}>0$ 
 

 

Bài 2:

 a) $t^{4}-t+\frac{1}{2}=(t^{4}-2t^{2}\frac{1}{2}+\frac{1}{4})+(t^{2}-t+\frac{1}{4}) \geq 0$

Bài viết đã được chỉnh sửa nội dung bởi tpdtthltvp: 23-03-2016 - 20:27

[tpdtthltvp]

                                                                                        ĐỀ THI SỐ 6  

Bài 4:

      a)  Cho tam giác $ABC$ với $\widehat{ABC}=\widehat{ACB}=50^{o}$. $N$ là điểm thuộc miền trong của tam giác thỏa mãn $\widehat{NBC}=10^{o},\widehat{NCB}=20^{o}$. Tính góc $ANB$ 
      b) Cho hình vuông $ABCD$ có cạnh bằng $1$. $M$ là điểm bất kì nằm trong hình vuông. Chứng minh $MA^2+MB^2+MC^2+MD^2 \ge 2$
 

Bài 4:

a) Dựng $\Delta AMC$ đều (như hình vẽ) $\Rightarrow \widehat{BCM}=\widehat{ACM}-\widehat{ACB}=10^o$

$\Delta ABM$ cân tại $A$ (vì $AB=AM=AC$) mà $\widehat{BAM}=\widehat{BAC}-\widehat{MAC}=80^o-60^o=20^o$

$\Rightarrow \Delta NBC=\Delta MCB(g.c.g)\Rightarrow BN=MC=AC=AB\Rightarrow \Delta ABM$ cân tại $A$ có $\widehat{ABN}=\widehat{ABC}-\widehat{NBC}=50^o-10^o=40^o$

$\Rightarrow \widehat{ANB}=\frac{180^o-\widehat{ABN}}{2}=70^o$

 

b) Kẻ $MH,MI,MK,MP$ lần lượt vuông góc với $AB,BC,AD,CD$

Ta có:

$$MA^2=AH^2+MH^2=MK^2+MH^2$$

Cmtt, ta có:

$$MA^2+MB^2+MC^2+MD^2=2(MH^2+MI^2+MP^2+MK^2)\geq 2.[\frac{(MH+MP)^2}{2}+\frac{(MK+MI)^2}{2}]=2.(\frac{HP^2}{2}+\frac{KI^2}{2})=2.(\frac{1}{2}+\frac{1}{2})=2$$

Bài viết đã được chỉnh sửa nội dung bởi tpdtthltvp: 23-03-2016 - 21:14

[NTA1907]

                                                                                        ĐỀ THI SỐ 6  

c) Cho $a,b,c$ là $3$ số nguyên khác $0$ thỏa $\frac{a}{b}+\frac{b}{c}+\frac{c}{a}=3$. Chứng minh tích $abc$ là lập phương của một số nguyên.

Áp dụng AM-GM cho 3 TH:

TH1: $a,b,c> 0

$\Rightarrow \frac{a}{b}+\frac{b}{c}+\frac{c}{a}\geq 3$

Dấu = xảy ra$\Leftrightarrow a=b=c> 0$

TH2: $a> 0; b,c< 0$

$\Rightarrow \frac{a}{-b}+\frac{-b}{-c}+\frac{-c}{a}\geq 3$

Dấu = xảy ra$\Leftrightarrow a=-b=-c> 0$

TH3: $a,b> 0; c< 0$

$\Rightarrow \frac{a}{b}+\frac{b}{-c}+\frac{-c}{a}\geq 3$

Dấu = xảy ra$\Leftrightarrow a=b=-c> 0$

$\Rightarrow$ đpcm

P/s: Anh nghĩ đề này quá khó đối với trình độ của học sinh lớp 8

Bài viết đã được chỉnh sửa nội dung bởi NTA1907: 24-03-2016 - 13:43

[lenadal]

Đề sáu bài hình có thể thành bài khó hơn :

Cho tam giác $ABC$  nhọn, giao ba đường phân giác của tam giác tại $I$. Qua $I$ kẻ một đường thẳng vuông góc với $CI$, cắt $CA$ và $CB$ lần lượt tại $M$ và $N$. cmr

 a. $\widehat{AMI}=\widehat{BNI}=\widehat{AMI}$ và $\Delta AMI$ đồng dạng với $\Delta INB$

b. $\frac{AM}{BN}=\left ( \frac{AI}{BI} \right )^{2}$

c. $\frac{AM}{AC}+\frac{BN}{BC}+\frac{CI^{2}}{AC\cdot BC}=1$

[Trung Kenneth]

                                                                                                                          ĐỀ THI SỐ 7

Câu 1: 

Cho biểu thức $A=(\frac{1}{3}+\frac{3}{x^2-3x}) :  (\frac{x^2}{27-3x^2}+\frac{1}{x+3})$

a, Rút gọn A

b, Tìm x để $A< -1$

c, Tìm x nguyên để A nguyên

Câu 2:

a, Tìm các chữ số a,b,c thỏa mãn : $\sqrt{\overline{abc}}-\sqrt{\overline{acb}}=1$\

b, Cho các số thực a,b,c khác 0 thỏa mãn $\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=\frac{1}{a+b+c}$

Chứng minh rằng: $\frac{1}{x^{2015}}+\frac{1}{y^{2015}}+\frac{1}{z^{2015}}=\frac{1}{x^{2015}+y^{2015}+z^{2015}}$

Câu 3:

a, Giải phương trình: $\frac{x^2+3x+3}{x^2-4x+3}+\frac{x^2+6x+3}{x^2+5x+3}= \frac{53}{12}$

b, Chứng minh rằng trong 144 số tự nhiên, mỗi số có 3 chữ số, bao giờ cũng chon được 2 số sao cho khi viết liền kề nhau được 1 số có 6 chữ sô chia hết cho 143

Câu 4:

Cho x,y,z >0 thỏa mãn $x+y+z=3$. Tìm min $P=\frac{1}{x^2+x}+\frac{1}{y^2+y}+\frac{1}{z^2+z}$

Câu 5:

Cho $\triangle ABC$ nhọn có 3 đường cao AF, BK, CE cắt nhau tại H. Kẻ Ax vuông góc AB, Cy vuông góc BC. P là giao điểm Ax và Cy.

a, Chứng minh AHCP là hình bình hành.

b, O,D,E lần lượt là trung điểm BP, BC, CA. CMR: $\triangle ODE\sim \triangle HAB$

c, G là trọng tâm của $\triangle ABC$. CMR: O,H,G thẳng hàng

d, Tìm vị trí điểm A sao cho AF.HF max

Bài viết đã được chỉnh sửa nội dung bởi tpdtthltvp: 24-03-2016 - 22:04

[tquangmh]

                                                                                        ĐỀ THI SỐ 6  

Bài 3:

      a) Giải phương trình $x^2(x^4-1)(x^2+2)+1=0$ 
      

Bài 5: Tìm giá trị nhỏ nhất của biểu thức $A$ biết rằng $a,b,c>0$ và $abc=1$. Và 
$A=\frac{a^2(b+c)}{b\sqrt{b}+c\sqrt{c}}+\frac{b^2(c+a)}{c\sqrt{c}+a\sqrt{a}}+\frac{c^2(a+b)}{a\sqrt{a}+b\sqrt{b}}$

 

 

Bài 3/a : 

Có : $x^{2}(x^{4}-1)(x^{2}+2)+1=0\Leftrightarrow x^{2}(x^{2}+1)(x^{2}-1)(x^{2}+2)=-1\Leftrightarrow (x^{4}+x^{2})(x^{4}+x^{2}-2)=-1$

Đặt : $y=x^{4}+x^{2}\geq 0$, ta có : $PT \Leftrightarrow y(y-2)+1=0 \Leftrightarrow y^{2}-2y+1=0\Leftrightarrow (y-1)^{2}=0 \Leftrightarrow y=1 \Leftrightarrow x^{4}+x^{2}-1=0$

Đến đây, đặt : $t=x^{2}\geq 0$ nên $PT \Leftrightarrow t^{2}+t-1=0 \Leftrightarrow \begin{bmatrix} t=\frac{-1+\sqrt{5}}{2} (nhận)\\t=\frac{-1-\sqrt{5}}{2} (loại) \end{bmatrix}$

Do đó : $t=\frac{-1+\sqrt{5}}{2}\Leftrightarrow x^{2}=\frac{-1+\sqrt{5}}{2} \Leftrightarrow x=\pm \sqrt{\frac{-1+\sqrt{5}}{2}}$

Vậy : $x=\pm \sqrt{\frac{-1+\sqrt{5}}{2}}$ là nghiệm của phương trình.

 

Bài 5 : 

Theo Bất đẳng thức Cô-si, có : 

$\sum \frac{a^{2}(b+c)}{b\sqrt{b}+c\sqrt{c}}\geq \sum \frac{2a^{2}\sqrt{bc}}{b\sqrt{b}+c\sqrt{c}}= 2.\sum \frac{\sqrt{a^{4}bc}}{b\sqrt{b}+c\sqrt{c}} = 2.\sum \frac{\sqrt{a^{3}}}{b\sqrt{b}+c\sqrt{c}} =2.\sum \frac{a\sqrt{a}}{b\sqrt{b}+c\sqrt{c}}$

Đổi biến : $(a\sqrt{a};b\sqrt{b};c\sqrt{c})\rightarrow (x;y;z)$

Ta có : $A \geq 2.\sum \frac{x}{y+z} \geq 2.\frac{3}{2}=3$ (theo Bất đẳng thức Nesbit cho ba số x, y, z dương)

Vậy : $minA=3 \Leftrightarrow a=b=c=1$

 

*Lưu ý : $a^{2}\sqrt{bc}= \sqrt{a^{4}bc}= \sqrt{a^{3}} (do:abc=1)$

 

P/S  : Ngóng câu 6 đề 6 ...

[I Love MC]

 

                                                                                        ĐỀ THI SỐ 6  

Bài 6:

       b) Chứng minh rằng với mỗi số tự nhiên $n$, giữa $n^2$ và $(n+1)^2$ có thể tìm được ba số tự nhiên $a,b,c$ sao cho $c|(a^2+b^2)$

 

Giải câu 6b trước cho các bạn hóng (đang bận ) 

Câu 6/b:

Đây là Olympic St Peterbuag dành cho các bạn học sinh lớp 8 bên Nga anh sưu tầm được 
Chọn $a=n^2+n+1,b=n^2+2$ và $c=n^2+1$ khi đó ta có bộ $(a,b,c)$  thỏa mãn đề

Bài viết đã được chỉnh sửa nội dung bởi tpdtthltvp: 24-03-2016 - 21:11

[tpdtthltvp]

 

                                                                                                                          ĐỀ THI SỐ 7

Câu 1: 

Cho biểu thức $A=(\frac{1}{3}+\frac{3}{x^2-3x}) :  (\frac{x^2}{27-3x^2}+\frac{1}{x+3})$

a, Rút gọn A

b, Tìm x để $A< -1$

c, Tìm x nguyên để A nguyên

 

Câu 2:

b, Cho các số thực a,b,c khác 0 thỏa mãn $\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=\frac{1}{a+b+c}$

Chứng minh rằng: $\frac{1}{x^{2015}}+\frac{1}{y^{2015}}+\frac{1}{z^{2015}}=\frac{1}{x^{2015}+y^{2015}+z^{2015}}$

 

Câu 3:

a, Giải phương trình: $\frac{x^2+3x+3}{x^2-4x+3}+\frac{x^2+6x+3}{x^2+5x+3}= \frac{53}{12}$

 

Câu 4:

Cho x,y,z >0 thỏa mãn $x+y+z=3$. Tìm min $P=\frac{1}{x^2+x}+\frac{1}{y^2+y}+\frac{1}{z^2+z}$

 

Câu 1:

a) ĐKXĐ: $x\neq 0;x\neq -3;x\neq 3$

Sau khi biến đổi, ta được 

$$A=-\frac{x+3}{x}$$

b) $A<-1\Leftrightarrow \frac{x+3}{x}>1\Leftrightarrow \frac{3}{x}>0\Leftrightarrow x>0$

Vậy với $x>0,x\neq 3$ thì $A<-1$

c)

$A\in Z\Leftrightarrow -\frac{x+3}{x}\in \mathbb{Z}\Leftrightarrow 3\vdots x\Rightarrow x\in \left \{ -1;1 \right \}$

 

Câu 2:

b) Ta có:

$\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=\frac{1}{a+b+c}\Leftrightarrow (ab+bc+ca)(a+b+c)-abc=0\Leftrightarrow (a+b)(b+c)(c+a)=0\Leftrightarrow \begin{bmatrix} a=-b \\ b=-c \\ c=-a \end{bmatrix}\Rightarrow \text{đpcm}$

 

Câu 3:

a) Dễ thấy $x=0$ không là nghiệm của PT. Với $x\neq 0$:

$\Rightarrow \frac{x+3+\frac{3}{x}}{x-4+\frac{3}{x}}+\frac{x+6+\frac{3}{x}}{x+5+\frac{3}{x}}=\frac{53}{12}$

Đặt $x+\frac{3}{x}=a\Rightarrow \frac{a+3}{a-4}+\frac{a+6}{a+5}=\frac{53}{12}$

Tới đây giải như bình thường!

 

Câu 4:

$\sum \frac{1}{x^2+x}=\sum \frac{1}{x(x+1)}=\sum (\frac{1}{x}-\frac{1}{x+1})=(\frac{1}{x}+\frac{1}{y}+\frac{1}{z})-(\frac{1}{x+1}+\frac{1}{y+1}+\frac{1}{z+1})\geq (\frac{1}{x}+\frac{1}{y}+\frac{1}{z})-\frac{1}{4}(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}+3)=\frac{3}{4}(\frac{1}{x}+\frac{1}{y}+\frac{1}{z})-\frac{3}{4}\geq \frac{3}{4}.\frac{9}{3}-\frac{3}{4}=\frac{3}{2}$

Bài viết đã được chỉnh sửa nội dung bởi tpdtthltvp: 24-03-2016 - 22:26

[I Love MC]

                                                                  ĐỀ THI SỐ 8 : 
Bài 1: (1,5 điểm) Cho các số thực dương $x,y,z$ thỏa mãn : 
$\begin{cases} &x^2+y^2=9&\\&y^2+z^2=16&\\&y^2=xz& \end{cases}$ 
Tính giá trị của $A=xy+yz$
 

Bài 2: Tìm nghiệm nguyên của các phương trình sau : 
     a) $x^2+2y^2+2xy+3y-4=0$ 
     b) $x^4+x^2-y^2+y+10=0$ 
 

Bài 3: Cho $a,b,c$ là các số thực dương có tổng bằng $2016$. Chứng minh : 
$\sum \frac{a^2+bc}{b+c} \ge 2016$ 
 

Bài 4: Tìm số lớn nhất trong ba số dương $x,y,z$ thỏa mãn hệ phương trình : 
$\begin{cases} &x=1-|1-2y|&\\&y=1-|1-2z|&\\&z=1-|1-2x|& \end{cases}$ 
 

Bài 5: Cho hình bình hành $ABCD$ . Trên các cạnh $BC,CD$ lần lượt lấy $M,N$ sao cho $\frac{BM}{CM}=\frac{CN}{2.DN}=k$. Gọi $P,Q$ theo thứ tự là giao điểm của $AM,AN$ với $BD$. 
a) Chứng minh : $S_{PMNQ}=S_{APQ}$ 
b) Tính $\frac{S_{AMN}}{S_{ABCD}}$ theo $k$ 
 

Bài 6: Có tồn tại hay không $2016$  số nguyên dương $a_1,a_2,..,a_{2016}$ để : 
$a_1^2+a_2^2,a_1^2+a_2^2+a_3^2,...,a_1^2+a_2^2+..+a_{2016}^2$ đều là số chính phương.

Bài viết đã được chỉnh sửa nội dung bởi tpdtthltvp: 27-03-2016 - 11:16