Em cập nhật bài mới thay anh Toàn vậy! ![]()
Lời giải bài tuần 1 tháng 4 đã được thầy Hùng đưa ra tại tuần 2 tháng 4 và kèm theo bài toán mới:
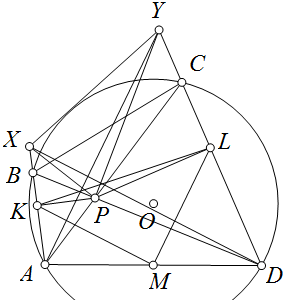
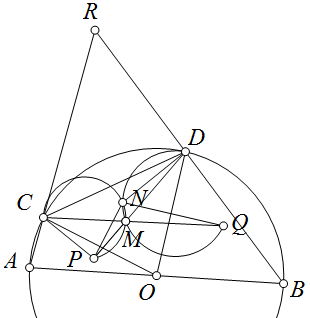
Bài 34. Cho tứ giác $ABCD$ nội tiếp đường tròn $(O)$ với $AC$ cắt $BD$ tại $P.M$ là trung $AD. K,L$ lần lượt là hình chiếu của $P$ lên $AB,CD$. Gọi $S,T$ lần lượt là tâm ngoại tiếp các tam giác $KMA$ và $LMD$. Chứng minh rằng: $KS.BT=CS.LT$.
Hình vẽ bài toán
Bài viết đã được chỉnh sửa nội dung bởi Nesbit: 18-04-2016 - 20:15
sửa link