TURKEY Team Selection Test 2016
Ngày 1 (02/04/2016)
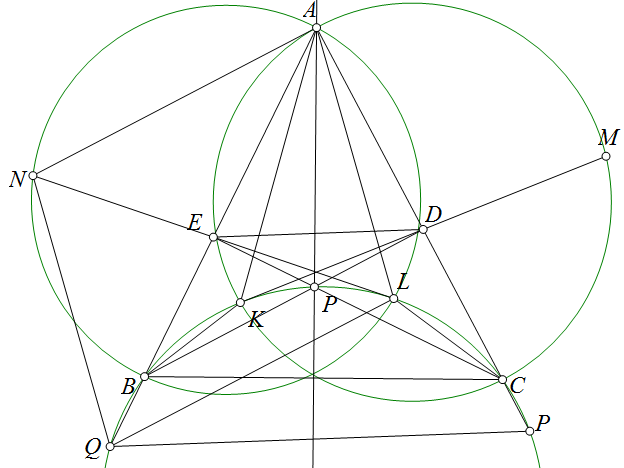
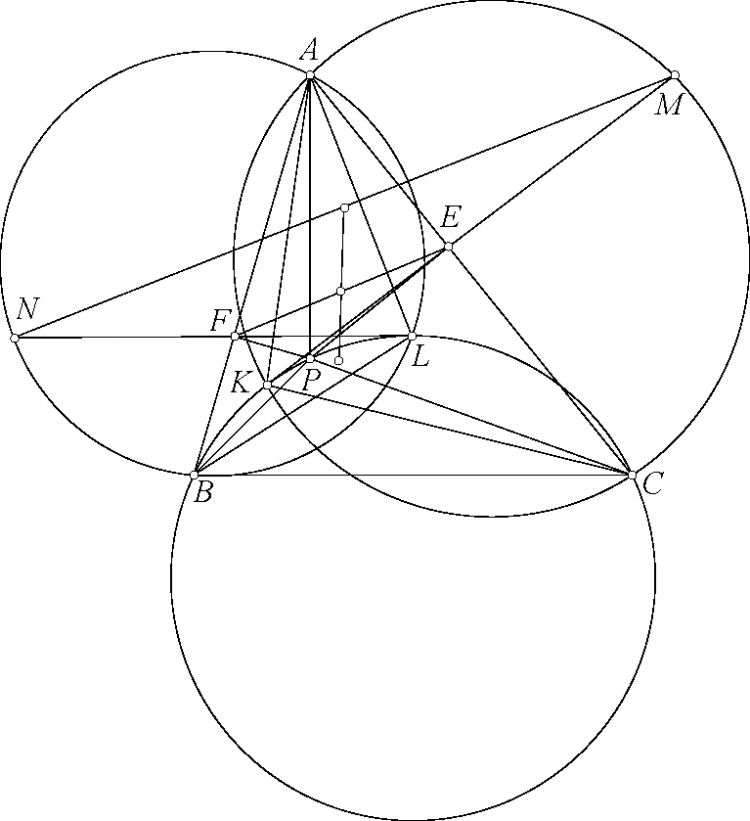
Bài 1. Cho tam giác $ABC$ nhọn, $P$ thuộc đường cao hạ từ $A$. Các đường thẳng $BP, CP$ lần lượt cắt các cạnh $CA, AB$ tương ứng tại $D, E$. Tiếp tuyến kẻ từ $D$ và $E$ tới $(BPC)$ tiếp xúc tại $K, L$ tương ứng ($K, L$ nằm trong tam giác). Đường thẳng $KD$ giao với $(AKC)$ tại $M$ ($M \neq K$) và đường $LE$ giao với $(ALB)$ tại $N$ ($N \neq L$). Chứng minh rằng $\frac{DK}{DM} = \frac{EL}{EN}$ khi và chỉ khi $P$ là trực tâm của tam giác $ABC$.
Bài 2. Trong một lớp học có $23$ học sinh, mỗi cặp học sinh đã coi một bộ phim cùng nhau. Với mỗi học sinh, các bộ phim học sinh đó coi gọi là tuyển tập các bộ phim của học sinh đó. Biết rằng mỗi học sinh đã coi mỗi bộ phim tối đa một lần, hỏi có ít nhất bao nhiêu tuyển tập các bộ phim khác nhau của những học sinh này?
Bài 3. Cho $a, b, c$ là các số thực không âm thỏa mãn $a^{2} + b^{2} + c^{2} \le 3$. Chứng minh rằng $$(a + b + c)(a + b + c - abc) \ge 2(a^{2}b + b^{2}c + c^{2}a)$$
Ngày 2 (03/04/2016)
Bài 4. Một dãy các số thực $a_{0}, a_{1}, \cdots$ thỏa mãn điều kiện $$\sum_{n = 0}^{m}a_{n}.(-1)^{n}.\binom{m}{n} = 0$$ với mọi số nguyên dương $m$ đủ lớn. Chứng minh rằng tồn tại một đa thức $P$ thỏa mãn $a_{n} = P_{n}$ với mọi $n \ge 0$.
Bài 5. Tìm tất cả hàm $f:\mathbb{N}\to\mathbb{N}$ sao cho với mọi $m, n \in \mathbb{N}$ thì $f(mn) = f(m).f(n)$ và $m + n \mid f(m) + f(n)$
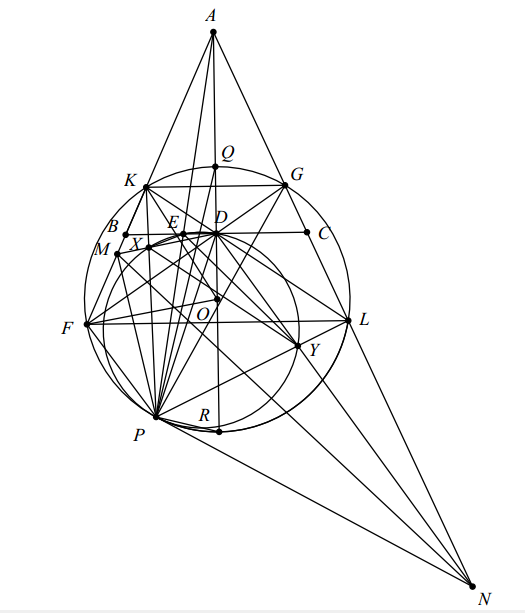
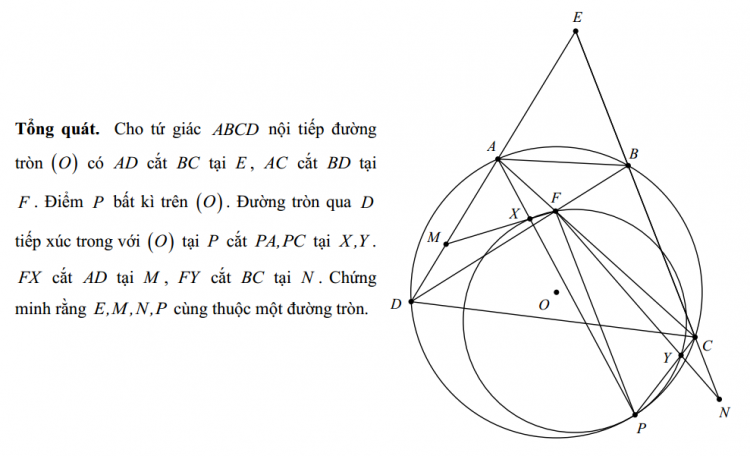
Bài 6. Cho tam giác $ABC$ cân tại $A$ với $D$ là trung điểm của $BC$. Một đường thẳng qua $D$ cắt $AB$ tại $K$, $AC$ tại $L$. Điểm $E$ trên cạnh $BC$ ($E \neq D$), $P$ trên $AE$ sao cho $\angle KPL = 90^{\circ} - \frac{1}{2}\angle KAL$; $E$ nằm giữa $A$ và $P$. Đường tròn ngoại tiếp tam giác $PDE$ cắt $PK$ tại $X$ ($X \neq P$) và cắt $PL$ tại $Y$ ($Y \neq L$). Đường $DX$ cắt $AB$ tại $M$, đường $DY$ cắt $AC$ tại $N$. Chứng minh rằng bốn điểm $P, M, A, N$ cùng thuộc một đường tròn.
Ngày 3 (04/04/2016)
Bài 7. Cho $A_{1}, A_{2}, \cdots , A_{k}$ là các tập con khác nhau của tập $\{1, 2, \cdots , 2016\}$. Nếu $A_{i} \cap A_{j}$ tạo thành một cấp số cộng với mỗi $1\le i \le j \le 2016$. Tìm giá trị lớn nhất có thể của $k$.
Bài 8. Các góc của một đa giác lồi $A_{1}A_{2}\cdots A_{n}$ ($n \ge 5$) là góc tù. Với mọi $1 \le i \le n$, $O_{i}$ là tâm ngoại tiếp của $A_{i - 1}A_{i}A_{i + 1}$ (quy ước $A_{0} = A_{n}$ và $A_{1} = A_{n + 1}$). Chứng minh rằng $O_{1}O_{2}\cdots O_{n}$ không phải là một $n$ - giác lồi.
Bài 9. $p$ là một số nguyên tố. Đặt $\mathbb{K}_{p}$ là tập hợp tất cả các đa thức hệ số nguyên thuộc tập $\{0, 1, \cdots , p - 1\}$ và bậc nhỏ hơn $p$. Giả sử với mọi cặp đa thức $P, Q \in \mathbb{K}_{p}$ sao cho $P(Q(n)) \equiv n\pmod{p}$ với mọi số nguyên $n$, thì bậc của $P$ và $Q$ là bằng nhau. Xác định mọi số nguyên tố $p$ thỏa mãn điều kiện trên.
Bài viết đã được chỉnh sửa nội dung bởi Ego: 01-05-2016 - 13:51