Chủ đề này có 6 trả lời

[baopbc]

$\boxed{\textrm{Bài toán}}$ (Thầy Trần Quang Hùng - Vietnam IMO Training 2016)

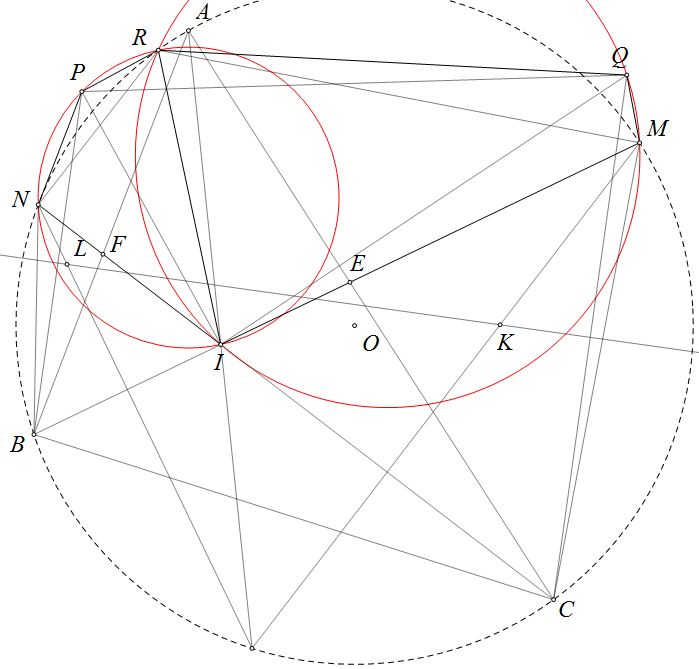
Cho tam giác $ABC$ nội tiếp $\odot (O)$. Phân giác $BE,CF$ cắt nhau tại $I$ và cắt $\odot (O)$ lần lượt tại $M,N.K,L$ lần lượt là tâm nội tiếp các tam giác $CME$ và $BNF.P,Q$ lần lượt là ảnh của $B,C$ qua $KL$. Chứng minh rằng nếu $\odot (IPN)$ và $\odot (IQM)$ cắt nhau tại $R$ thuộc $\odot (O)$ thì $\angle PRQ-\frac{\angle BAC}{4}$ không đổi.

P.s: Mình đoán là $135^\circ$! Ai có cách dựng thật chuẩn và lời giải thì post lên nhé!

Hình vẽ bài toán

Bài viết đã được chỉnh sửa nội dung bởi baopbc: 06-05-2016 - 20:36

[quanghung86]

Cám ơn Bảo đã post lại, bài này là chủ yếu kiểm tra kỹ năng dựng hình và phán đoán hình của các thành viên đội tuyển. Sau một số gợi ý của thầy thì các bạn đã làm được bài này trong vòng 1h.

[baopbc]

Cám ơn Bảo đã post lại, bài này là chủ yếu kiểm tra kỹ năng dựng hình và phán đoán hình của các thành viên đội tuyển. Sau một số gợi ý của thầy thì các bạn đã làm được bài này trong vòng 1h.

Thầy có thể đưa ra một số gợi ý cho bài này được không ạ!

Em hơi bí!   

[Nguyen Dinh Hoang]

Bảo có thể up hình vẽ gần đúng lên được không Bảo để dễ hình dung cảm ơn Bảo trước, mình đã phát hiện 1 số tính chất nhưng vẫn chưa có ý tưởng cm

Bài viết đã được chỉnh sửa nội dung bởi Nguyen Dinh Hoang: 06-05-2016 - 20:37

[baopbc]

Mình có một mở rộng rất đẹp cho bài toán.

Ta có: $\angle PQR-\angle BAC/4=\angle MRN+\angle PIN+\angle QIM-\angle BAC/4$

$=90^\circ+\angle BAC/2-\angle BAC/4+\angle PIN+\angle QIM$.

Dự đoán $\angle PQR-\angle BAC/4=135^\circ$ nên $\angle BAC/2+2\angle PIN+2\angle QIM=90^\circ$. Gọi $D$ là điểm chính giữa cung $BC$ không chứa $A.Y,Z$ lần lượt là giao của $BL,CK$ với $\odot (O)$. Đẳng thức trên tương đương với $\angle YDZ=\angle PIN+\angle QIM$. 

Bài toán mở rộng.

Cho tam giác $ABC$ nội tiếp $\odot (O)$. Phân giác $\angle B,C$ lần lượt cắt $\odot (O)$ tại $M,N.D$ là điểm chính giữa cung $BC$ không chứa $A.K,L$ bất kì thuộc $DN,DM.P,Q$ lần lượt là điểm đối xứng của $B,C$ qua $KL.BK,CL$ cắt $\odot (O)$ lần lượt tại $Y,Z$. Chứng minh $\angle YDZ=\angle PIN+\angle QIM$.

Hình vẽ

Lời giải dưới của bạn Nguyen Dinh Hoang và lời giải gốc không dùng được trong trường hợp tổng quát này!

Bài viết đã được chỉnh sửa nội dung bởi baopbc: 07-05-2016 - 17:19

[Nguyen Dinh Hoang]

Lời giải của em cho bài toán. Em sẽ cố up bằng $LateX$ sớm nhất vì em chưa có máy mong mọi người thông cảm ạ!

Bài viết đã được chỉnh sửa nội dung bởi Nguyen Dinh Hoang: 08-05-2016 - 09:46

[quanghung86]

Ý tưởng chính ở đây là đối xứng trục $KL$ và cái chính là cần tính góc $\angle PIQ$. Vậy ta sẽ làm ngược lại lấy $J$ đối xứng $I$ qua $KL$. Ta cần tính $\angle BJC$. Đến đây bài toán đơn giản vì chú ý $K$ là tâm $(JIC)$ và $L$ là tâm của $(JIB)$. Từ đó dùng tính chất góc ở tâm dễ thấy $\angle PIQ=\angle BJC=45^\circ+\frac{3}{4}\angle BAC$. Từ đó nếu giao điểm $R$ khác $I$ của $(IPN)$ và $(IQM)$ nằm trên $(O)$ thì $\angle PRQ=\angle PRN+\angle NRM+\angle MRQ=2\angle BIC-\angle PIQ=135^\circ+\frac{\angle BAC}{4}$. Đến đây hoàn tất cm.

 

Chú ý ý tưởng đối xứng trục rất thú vị, nếu không có đx trục vẫn tính được những sẽ rất dài. Điểm mấu chốt vẫn là tính $\angle BJC$.