Chủ đề này có 434 trả lời

[quanghung86]

Bài toán 61 lời giải trên báo dùng phương tích cũng rất hay, lời giải này và của Quân (halloffame) đều khác với đáp án mình làm. Ai có thể đưa lời giải của báo lên không ?

 

Có một lưu ý nhỏ là bài toán 60 có nguồn gốc từ tạp chí Mathematical Reflections, sau đó nó được Telv Cohl tổng quát trên AoPS như sau

 

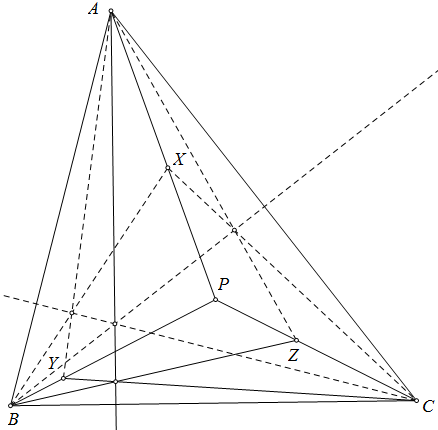
$\boxed{\text{Bài toán 60'.}}$ Cho tam giác $ABC$ nội tiếp $(O)$. Các đường tròn mixtilinear nội ứng với $A,B,C$ là $(O_a),(O_b),(O_c)$ lần lượt tiếp xúc $(O)$ tại $D,E,F$. $P$ nằm trên đường thẳng $OI$. $PD,PE,PF$ lần lượt cắt $(O_a),(O_b),(O_c)$ tại điểm thứ hai $X,Y,Z$. Chứng minh rằng $AX,BY,CZ$ đồng quy.

 

Trường hợp bài toán 60 là khi $P$ trùng $O$. Tuy nhiên bài toán tổng quát này khá khó, mình đưa lên là để cùng thảo luận, biết đâu có một lời giải hay cho bài này. Mặc dù vậy bài toán 60 gốc cũng đủ hay.

Bài viết đã được chỉnh sửa nội dung bởi halloffame: 30-12-2017 - 13:48

[TQHKTH]

Thượng úy Dogsteven đưa ra một bài toán rất hay mà hình như chưa có ai giải phải ko ạ (post #131)?

Em có một bài toán tương tự khác.

Cho tam giác $ABC$ và điểm $P$ nằm trên trung trực $BC$, đường tròn ngoại tiếp tam giác $(PBC)$ cắt $AB, AC$ tại $F, E$. Gọi $Q$ là điểm đẳng giác của $P$ trong tam giác $ABC$. Khi đó $PQ, BE, CF$ đồng quy.

Mình xin đề xuất hướng tiếp cận của mình như sau:

Chứng minh. Gọi $BE\cap CF = K$ và đặt $\angle PBC = \angle PCB = \alpha$. Dễ dàng cộng góc để suy ra $\angle PEB = \angle PFC = \angle QBA = \angle QCA = \angle PEA = \angle PFA = \alpha$. Dựng $S, T\in CA, AB$ sao cho $\angle EKS = \angle FKT = \alpha$. Khi đó: $BECF$ nội tiếp nên $\triangle KCE \sim \triangle KBF$. Từ đây ta có 2 cấu hình đồng dạng:

$(\triangle KCE\cup S)\sim (\triangle KBF\cup T)$

Do đó: $(CE,S) = (BF,T)$. Lại chú ý tới 1 loạt các góc bằng $\alpha$ ở trên, ta có $CQ\parallel EP\parallel SK$ và $BQ\parallel FP\parallel TK$ nên theo Thales đảo dễ thấy $\overline{Q,P,K}$. Vậy kết thúc chứng minh.

Hình gửi kèm

• 

[Ngockhanh99k48]

$\boxed{\text{Lời giải bài toán 60'}}$

$AI, BI, CI$ thứ tự cắt $(O)$ tại các điểm thứ hai $A_1, B_1, C_1$. $DP, EP, FP$ thứ tự cắt $(O)$ tại các điểm thứ hai $D_1, E_1, F_1$. Một tính chất quen thuộc của đường tròn Mixtilinear là $AD, BE, CF$ đi qua tâm vị tự ngoài $Q$ của $OI$. 

Áp dụng định Pascal cho 6 điểm đồng viên $\begin{pmatrix} A & E & D_1 \\ B & D &E_1 \end{pmatrix}$ ta có $AE_1$ cắt $BD_1$ tại một điểm $R$ thuộc $PQ$. Do $P, Q$ đều thuộc đường thẳng $OI$ nên ta có $R$ thuộc $OI$.

Lại áp dụng định lí Pascal cho 6 điểm đồng viên $\begin{pmatrix} A & B_1 & D_1 \\  B & A_1 & E_1 \end{pmatrix}$ ta có $A_1D_1$ cắt $B_1E_1$ tại $S$ thuộc $IR$. Do $IR \equiv OI$ nên $S$ thuộc đường thẳng $OI$. Tương tự ta sẽ suy ra được $A_1D_1, B_1E_1, C_1F_1$ đồng quy tại $S$ thuộc $OI$.

Áp dụng định lí Ceva trong đường tròn ta có $\frac{D_1B_1}{D_1C_1}.\frac{E_1C_1}{E_1A_1}.\frac{F_1A_1}{F_1B_1}=1$.

Đường tròn $(O_a)$ tiếp xúc $AB, AC$ thứ tự tại $A_b, A_c$. Đương nhiên ta có $D, A_b, C_1$ và $D, A_c, B_1$ thẳng hàng

Phép vị tự tâm $D$: $V_{D}^{\frac{DO_a}{DO}}: D_1 \rightarrow X, C_1 \rightarrow A_b, B_1 \rightarrow A_c$, kết hợp $XA$ là đường đối trung của $\triangle XA_bA_c$, ta suy ra $\frac{\sin\widehat{XAA_b}}{\sin\widehat{XAA_c}}=\frac{XA_b^2}{XA_c^2}=\frac{D_1C_1^2}{D_1B_1^2}$. Lập các công thức tương tự ta có $AX, BY, CZ$ đồng quy tại $T$.

Một tính chất của $T$: Khi $P$ chạy trên đường thẳng $OI$, liên hợp đẳng giác của $T$ đối với $\triangle ABC$ chạy trên đường ellipse nội tiếp $\triangle ABC$ (inellipse).

 

 

[halloffame]

$\boxed{\text{Bài toán 62}}$

Cho tam giác $ABC$ có đường cao $AH$ và đường tròn nội tiếp $(I)$ tiếp xúc $AC$ ở $E.(A;AE)$ cắt $AH$ ở $M.MI$ cắt $BC$ ở $T.$

Chứng minh đường tròn đường kính $AT$ tiếp xúc với $(I).$

Bài viết đã được chỉnh sửa nội dung bởi halloffame: 05-07-2016 - 11:55

[Ngockhanh99k48]

$\boxed{\text{Lời giải bài toán 62}}$

Đường thẳng $IM, DM$ thứ tự cắt $(A; AE)$ tại điểm thứ hai $X, N$. Kẻ tiếp tuyến $Mt$ của $(A; AE)$. Ta có $Mt \parallel BC$. Do đó $\widehat{XNM}=\widehat{XMt}=\widehat{XTD}$, ta suy ra $T, N, D, X$ đồng viên và $\widehat{DNT}=\widehat{DXT}$.
Mặt khác $IM.IX=IE^2=ID^2$. Do đó $\widehat{DXT}=\widehat{IDM}=\widehat{AMN}=\widehat{ANM}$, hay $\widehat{DNT}=\widehat{MNA}$. Do đó $N, A, T$ thẳng hàng.
Gọi $K$ là giao điểm của $(AMN)$ và $(I)$ sao cho $K$ khác phía $A$ với $MN$. $AK$ cắt $DN$ tại $L$. Ta có $AK.AL=AM^2=AE^2$ do $K$ thuộc $(I)$ nên $L$ thuộc $(I)$. Mặt khác $\widehat{KNA}=\widehat{NLA}=\widehat{KLD}=\widehat{KDB}$. Do đó $K \in (NXDT)$. Suy ra $\widehat{KAM}=\widehat{KND}=\widehat{KTD}$, hay $K \in (AHT) \equiv (AT)$. Lại có $\widehat{DKT}=\widehat{DNT}=\frac{\widehat{HAT}}{2}=\frac{\widehat{HKT}}{2}$. Do đó $KD$ là phân giác $\widehat{HKT}$.
Kẻ tiếp tuyến $Kx$ của $(I)$. Bằng cộng góc suy ra $Kx$ cũng là tiếp tuyến của $(AT)$. Do đó ta có đpcm.

Thầy (hoặc bạn nào đó) có thể đề xuất bài mới giúp em (mình) được không ạ?

Thầy Hùng có thể dẫn lại đường link bài 60' của Telv được không ạ?

Bài viết đã được chỉnh sửa nội dung bởi viet nam in my heart: 06-07-2016 - 12:18
Thêm hình

[TQHKTH]

Nói thêm một chút, theo mình biết, bài toán 62 đã có ở đây và được mở rộng tại đây (post #78)

[baopbc]

Đề xuất bài toán tiếp theo khá nhẹ nhàng!

$\boxed{\text{Bài toán 63}}$ (AoPS) Cho tam giác $ABC$ nội tiếp $(O)$. Phân giác $\angle A$ cắt trung trực $CA,AB$ tại $M,N.H$ là trực tâm tam giác $OMN$. Chứng minh rằng $AH$ chia đôi $BC$.

[Nguyen Dinh Hoang]

$\boxed{\text{Lời giảibài toán 63}}$

Ta có $AM$ $=$ $\frac{\frac{AB}{2}}{cos\frac{A}{2}}$. Gọi $T$ là điểm chính giữa cung nhỏ $BC$. ta có theo công thức đường phân giác thì $AM$ $=$ $NT$. Nên trung điểm của $MN$ cũng là trung điểm của $AT$. Mặt khác ta dễ có $ONM$ cân tại $O$ nên đường cao đồng thời là trung tuyến.  

Gọi $G$ là trung điểm $BC$, $S$ là trung điểm $MN$ $OS$ cắt $AG$ tại $K$ áp dụng định lý $Menelaus$ cho tam giác $OTS$ cát tuyến $A, K, G$ ta có $\frac{1}{2}. \frac{GT}{GO}.\frac{KO}{KS} = 1$ nên $\frac{KO}{KS}$ $=$ $2$ . $\frac{GO}{GT}$. Gọi $U$ là điểm chính giữa cung lớn $BC$ thì 2 tam giác $OMN$ và $UBC$ đồng dạng vậy gọi $R$ là trực tâm tam giác $UBC$ thì $\frac{HO}{HS} = \frac{RU}{RG}$ $=$ $2$ $.\frac{GO}{GT}$ $=$ $\frac{KO}{KS}$ nên ta có điều phải chứng minh.

Bài viết đã được chỉnh sửa nội dung bởi halloffame: 30-12-2017 - 13:51

[anhquannbk]

$ \boxed{\text{Lời giải bài toán 63}}$

Gọi $D$ là trung điểm $BC$, $E$ là điểm chính giữa cung $BC$ không chứa $A$ của $(O)$ , $F$ là trung điểm $MN$.

Gọi $I$ là tâm đường tròn nội tiếp tam giác $MNP$

$P$ là giao điểm của $BM$ và $CN$

Ta có $ \angle IMN =\dfrac{1}{2} \angle BMN= \dfrac{1}{2} (\angle BAM+ \angle ABM) =\dfrac{1}{2} \angle BAC$.

và $\angle HMN = 90^0 -\angle ONM =\dfrac{1}{2} \angle BAC$

Suy ra $\angle IMN =\angle HMN$. Tương tự ta được $I, H$ đối xứng nhau qua $AE$.

Do đó $F$ cũng là trung điểm $AE$.

Ta có $\dfrac{HO}{HF}= \dfrac{FO}{FH}-1=\dfrac{MF.cot \dfrac{A}{2}}{MF.tan\dfrac{A}{2}}-1 =\dfrac{2cos^2\dfrac{A}{2}-1}{1-cos^2\dfrac{A}{2}}$.

$\dfrac{DE}{DO}=\dfrac{R(1-cosA)}{RcosA} =\dfrac{2-2cos^2\dfrac{A}{2}}{2cos^2\dfrac{A}{2}-1}$

Suy ra $\dfrac{AF}{AE}. \dfrac{DE}{DO}.\dfrac{HO}{HF}=1$

Theo định lý $Menelaus$ cho tam giác $OME$ thì $A, H, D$ thẳng hàng.

hay $AH$ chia đôi $BC$.

Nếu phát biểu thêm gọi $S$ là giao điểm hai đường tiếp tuyến tại $B$ và $C$ của $(O)$ thì $AS$ là đường đối trng của tam giác $ABC$. Chứng minh $SA$ đi qua $I$.

và đây là bài toán chọn đội tuyển THPT chuyên sư phạm $2011-2012$ và olympic Đồng bằng Bắc Bộ năm nay.

Bài viết đã được chỉnh sửa nội dung bởi anhquannbk: 06-07-2016 - 10:43

[quanghung86]

Đây là link gốc bài toán 60' 

 

http://www.artofprob...unity/c6h612592

[quanghung86]

$\boxed{\text{Bài toán 64.}}$ Cho tam giác $ABC$ nội tiếp trong đường tròn $(O)$. $P$ bất kỳ nằm trong tam giác. $PB,PC$ lần lượt cắt $(O)$ tại $E,F$ khác $B,C$. $M,N$ lần lượt là đối xứng của $B,C$ qua $AF,AE$. $K$ là tâm ngoại tiếp tam giác $PMN$. Gọi $L$ đối xứng $K$ qua trung trực $AP$. Chứng minh rằng $PL\parallel AO$ khi và chỉ khi $\frac{PB}{PC}=\frac{AB}{AC}$.

[baopbc]

$\boxed{\text{Lời giải bài toán 64}}$

Theo kết quả ELMO (#13) ta suy ra $AK\perp EF.X\equiv AK\cap EF$.

$PL\parallel AO$ khi và chỉ khi $AP$ là phân giác $\angle OAX$ hay $AP$ là phân giác $\angle EAF$

Mặt khác theo kết quả IMO 2010 (Problem 4) ta có điều phải chứng minh.$\blacksquare$

 

Đề nghị bài toán mới.

$\boxed{\text{Bài toán 65}}$ (AoPS) Cho tam giác $ABC$ với $\angle A\neq 90^\circ$ nội tiếp đường tròn $(O).D$ bất kì trên $BC$. Trung trực $AD$ cắt $OA$ tại $T.TD$ cắt $OB,OC$ tại $E,F$. Kí hiệu $\omega$ là đường tròn qua $A,D$ lần lượt tiếp xúc với $TA,TD$. Chứng minh rằng đường tròn $(OEF)$ tiếp xúc $\omega$

Bài viết đã được chỉnh sửa nội dung bởi baopbc: 06-07-2016 - 15:51

[Ngockhanh99k48]

$\boxed{\text{Lời giải bài toán 65}}$
Đường thẳng qua $O$ song song $BC$ cắt $AD$ tại $I$. $AD$ cắt $(O)$ tại điểm thứ hai $X$. Khi đó $TD \parallel OX$. $OB, OC$ thứ tự cắt $AD$ tại $Z, Y$. Ta có sẵn $OI$ là phân giác $\widehat{EOF}$. Ta có $\frac{IY}{ID}=\frac{OY}{OC}=\frac{OY}{OX}=\frac{FY}{FD}$. Do đó $FI$ là phân giác $\widehat{DFY}$. Hay $I$ là tâm bàng tiếp đỉnh $O$ của $\triangle OEF$. Từ đó áp dụng bổ đề Sawayama-Thebault ta có đpcm.
P/s: Bảo tiếp tục giúp anh nhé

[baopbc]

Lời giải bài toán 65 có thể tham khảo thêm lời giải khác của anh Huy tại đây.

Theo đề nghị của anh Khánh, đề xuất bài toán tiếp theo.

$\boxed{\text{Bài toán 66}}$ (AoPS) Cho hai đường tròn $(O),(O')$ có tâm vị tự ngoài $V.l$ là đường thẳng qua $V$ vuông góc với $OO'$. Hai điểm $P,Q$ trên $(O),(O')$ sao cho $V,P,Q$ thẳng hàng. Tiếp tuyến tại $P$ của $(O)$ cắt tiếp tuyến tại $Q$ của $(O')$ tại $X.XP,XQ$ cắt $l$ theo thứ tự tại $Y,Z$. Chứng minh rằng khi $P,Q$ thay đổi thì đường tròn ngoại tiếp tam giác $XYZ$ tiếp xúc với một đường tròn cố định.

 

Bài viết đã được chỉnh sửa nội dung bởi baopbc: 06-07-2016 - 16:39

[Nguyen Dinh Hoang]

Lời giải bài 66. Ta có các tứ giác $QO'VZ$ và $OPVY$ nội tiếp
Gọi $E$ là giao của $QO'VZ$ và $OPVY$ ta có $\angle OEV = 180^{\circ} - \angle OPV$ mà $\angle O'EV = 180 - \angle O'QV$ nên $EV$ là tia phân giác ngoài của $O'EO$ nên gọi $S$ là tâm vị tự trong của $(O)$ và $(O')$ thì $E$ nằm trên $(SV)$ mà ta có $E$ là điểm $Miquel$ của tứ giác toàn phần $XZVP,QY$ nên $E$ nằm trên $(XYZ)$ do $QO'VZ$ và $OPVY$ nội tiếp nên $EV$ là tia phân giác $ZEY$ tương tự ta có $(XYZ)$ tiếp xúc với đường tròn đường kính $SV$

Thầy hoặc bạn khác có thể đề xuất bài mới giúp em (mình) với ạ!

Bài viết đã được chỉnh sửa nội dung bởi halloffame: 30-12-2017 - 13:51

[baopbc]

Theo yêu cầu của bạn Nguyen Dinh Hoang, xin đề xuất bài toán mới. 

$\boxed{\text{Bài toán 67}}$ (Trần Quang Hùng ~ Nguyễn Đức Bảo) Cho tam giác $ABC$. Một đường tròn $(K)$ qua $B,C$ cắt $CA,AB$ tại $E,F.H$ là giao điểm của $BE,CF$. Kẻ $HL\perp AK,LD\perp BC.M$ là trung điểm $BC.AK$ cắt $(CL)$ tại $N$. Đường thẳng qua $A$ song song với $CH$ cắt trung trực $AN$ tại $Q$

Chứng minh rằng $(Q,QA),(CL),(MD)$ đồng quy.

 

Mô hình bài toán này khá giống với một bài toán mình đề nghị trong topic, tất cả đều dựa trên mô hình bài toán ??? của thầy Trần Quang Hùng!

 

Nguồn gốc bài 66: http://www.artofprob...1108467p5035848

Bài viết đã được chỉnh sửa nội dung bởi baopbc: 07-07-2016 - 09:07
Thêm Nguồn

[dogsteven]

$\boxed{\text{Bài toán 67}}$

Gọi $G$ là giao điểm của $AD$ với $(Q, QA)$ thì theo kết quả bài toán ??? ta suy ra $G$ thuộc $(DM)$

$AX$ là đường kính của $(Q, QA)$, khi đó cũng theo kết quả bài toán ??? ta có tam giác $MCX$ và $DLA$ đồng dạng.

Ngoài ra $TMX$ và $TDA$ đồng dạng nên $\dfrac{TM}{MC}=\dfrac{TM}{MX}:\dfrac{MC}{MX}=\dfrac{TD}{DA}:\dfrac{DL}{DA}=\dfrac{TD}{DL}$

Mà $LD\perp BC$ nên $\widehat{LDT}=\widehat{TMC}$

Do đó hai tam giác $TDL$ và $TMC$ đồng dạng, do đó $T\in (LC)$

Nhờ thầy và các bạn đề nghị bài toán tiếp theo.

Bài viết đã được chỉnh sửa nội dung bởi baopbc: 07-07-2016 - 19:40

[baopbc]

Lời giải đầy đủ bài toán 67 có thể tham khảo link.

 

Theo đề nghị của anh Dogsteven mình xin đề xuất bài toán mới sau.

$\boxed{\text{Bài toán 68}}$ (AoPS) Cho tam giác $ABC$ với tâm đường tròn $Euler$ là $N.D,E,F$ là hình chiếu của $N$ lên $BC,CA,AB$. Chứng minh rằng đường thẳng $Euler$ của các tam giác $AEF,BFD,CDE,ABC$ đồng quy.

[dogsteven]

Lời giải đầy đủ bài toán 67 có thể tham khảo link.

 

Theo đề nghị của anh Dogsteven mình xin đề xuất bài toán mới sau.

$\boxed{\text{Bài toán 68}}$ (AoPS) Cho tam giác $ABC$ với tâm đường tròn $Euler$ là $N.D,E,F$ là hình chiếu của $N$ lên $BC,CA,AB$. Chứng minh rằng đường thẳng $Euler$ của các tam giác $AEF,BFD,CDE,ABC$ đồng quy.

 

Bài này chính là một bài trong đề thi 30/4 lớp 10 năm nay. 

[baopbc]

Xin lỗi về sự trùng lặp, mình xin đề xuất lại một bài toán khác như sau.

 

$\boxed{\text{Bài toán 69}}$. Cho tam giác $ABC.P$ là một điểm bất kì trong tam giác $ABC.$ Trên $PA,PB,PC$ lần lượt lấy các điểm $X,Y,Z$ sao cho $AY,BX$, đường thẳng qua $C$ vuông góc $AB$ đồng quy, $AZ,CX$, đường thẳng qua $B$ vuông góc với $AC$ đồng quy. Chứng minh rằng $BZ,CY$, đường thẳng qua $A$ vuông góc $BC$ đồng quy.

Vừa mới chế ra, nếu trùng lặp ở đâu xin mọi người thứ lỗi!

 

Bài viết đã được chỉnh sửa nội dung bởi baopbc: 07-07-2016 - 20:22