Chủ đề này có 434 trả lời

[lucifer97]

Bài 76

câu a có bài tổng quát được thầy Hùng phát biểu ở đây

Mình xây dựng và phát biểu lại như sau : Cho tam giác $ABC$ nội tiếp $(O)$. Trung trực $BC$ giao $AB, AC$ tại $E, F$. Đường tròn tâm $I$ đường kính $EF$ giao tiếp tuyến tại $A$ của $(O)$ ở $M,N$ thì $(IMN)$ tiếp xúc $(O)$

Chú ý tính chất trực giao của $(AMN)$ và $(O)$. Mình che đi $(O)$ và phát biểu bài toán mới theo $(AMN)$

câu b là một trường hợp đặc biệt của bài toán sau:
Cho $(I)$ và $(O)$ giao nhau tại $BC. A$ di động trên $(O). AB, AC$ cắt $(I)$ tại $E, F$ thì $(AEF)$ tiếp xúc với $2$ đường tròn cố định đồng tâm $I$. Hơn nữa $2$ đường tròn này cũng tiếp xúc với $(O)$ !

Trong bài toán, do tình cờ nên $(ILK)$ đi qua tâm $Q$ ( theo lời giải bạn khanh) nên chỉ còn lại $1$ đường tròn ( ta có thể xem $(ILK)$ tiếp xúc với $(Q,0)$ và $(Q,QO)$)

Bài viết đã được chỉnh sửa nội dung bởi viet nam in my heart: 10-07-2016 - 15:04
Sửa tên bài

[viet nam in my heart]

Bài toán $77$ do Bảo đề nghị có lẽ được tạo ra nhờ bài toán sau: Cho tam giác $XYZ$ ngoại tiếp $(O)$. Các tiếp điểm của $(O)$ trên $YZ,ZX,XY$ là $A,B,C$. Một đường tròn tâm $O$ bất kỳ cắt tia đối của các tia $OA,OB,OC$(hoặc cắt các tia $OA,OB,OC$) lần lượt tại $L,M,N$.Khi đó $XL,YM,ZN$ đồng quy 

Bài này có lẽ đã cũ nhưng em(mình) chưa tìm được một lời giải nào hay, tính toán ít nên nhờ thầy và mọi người giúp đỡ

Bài viết đã được chỉnh sửa nội dung bởi viet nam in my heart: 10-07-2016 - 15:05

[QuangDuong12011998]

 

vietnam in my heart đã viết

"Bài toán 

7777 do Bảo đề nghị có lẽ được tạo ra nhờ bài toán sau: Cho tam giác XYZXYZ ngoại tiếp (O)(O). Các tiếp điểm của (O)(O) trên YZ,ZX,XY là A,B,C. Một đường tròn tâm O bất kỳ cắt tia đối của các tia OA,OB,OC(hoặc cắt các tia OA,OB,OC) lần lượt tại L,M,N. Khi đó XL,YM,ZN đồng quy 

Bài này có lẽ đã cũ nhưng em(mình) chưa tìm được một lời giải nào hay, tính toán ít nên nhờ thầy và mọi người giúp đỡ  :)"

 

Thực ra $\triangle XYZ$ và $\triangle LMN$ trực giao(orthologic) và có 2 tâm trực giao(orthology center) trùng nhau (chính là $O$), nên theo định lý Sondat, hai tam giác trực giao có tâm trực giao trùng nhau thì thấu xạ. Chứng minh cho trường hợp này có thể xem cho bài tổng quát hơn tại post #2 http://artofproblems...1181784p5767010

Bài viết đã được chỉnh sửa nội dung bởi QuangDuong12011998: 10-07-2016 - 17:06

[dogsteven]

Bài toán $77$ do Bảo đề nghị có lẽ được tạo ra nhờ bài toán sau: Cho tam giác $XYZ$ ngoại tiếp $(O)$. Các tiếp điểm của $(O)$ trên $YZ,ZX,XY$ là $A,B,C$. Một đường tròn tâm $O$ bất kỳ cắt tia đối của các tia $OA,OB,OC$(hoặc cắt các tia $OA,OB,OC$) lần lượt tại $L,M,N$.Khi đó $XL,YM,ZN$ đồng quy 

Untitled.png

Bài này có lẽ đã cũ nhưng em(mình) chưa tìm được một lời giải nào hay, tính toán ít nên nhờ thầy và mọi người giúp đỡ

 

Em cũng muốn một lời giải đẹp cho bài toán này chứ cứ phải áp dụng cái định lý gì đó để chứng minh định lý Sondat thì vất vả lắm. Mong thầy và anh chị giúp ạ.

[quanghung86]

Bài toán mà viet nam in my heart, nói có 3 hướng tiếp cận khác nhau

 

- Phương pháp vector : Biểu diễn vector $\vec{XL}$ theo $\vec{XY},\vec{XZ}$ và $k$ với $\vec{OL}=k\vec{OA}$ rồi chiếu xuống $XY$.

 

- Hàng điều hòa: Có thể bắt chước tương tự cách chứng minh đẳng giác của điểm Nagel nằm trên đường thẳng $OI$ (của tam giác $XYZ$), giờ ta sẽ chỉ ra $XL$ là đẳng giác trong góc $X$ của $XJ$ với $J$ là một điểm xác định trên đường thẳng $OI$.

 

- Giải bài tổng quát hơn: chính là bổ đề đã có ở đây http://analgeomatica...1-thang-12.html

 

Từ đó đến bài của Bảo ta làm như sau

 

Gọi $U,V,W$ đối xứng $A,B,C$ qua $D,E,F$ thì $XU,YV,ZW$ đồng quy. Dễ thấy phép vị tự tâm $O$ tỷ số 3 biến đường thẳng qua trung điểm $AX$ và $D$ thành $XU$. Từ đó dễ thấy các đường thẳng mới đồng quy.

Hình gửi kèm

• 

Bài viết đã được chỉnh sửa nội dung bởi quanghung86: 10-07-2016 - 18:40

[quanghung86]

$\boxed{\text{Bài toán 78.}}$ Cho tam giác $ABC$ có các tâm bàng tiếp góc $B,C$ là $K,L$. Lấy $P,Q$ trên $CK,BL$ sao cho $LP\parallel AC,KQ\parallel AB$. $PQ$ cắt $KL$ tại $R$. $H$ là hình chiếu của $R$ lên đường thẳng $OI$ của tam giác $ABC$. $AD$ là phân giác của tam giác $ABC$. $K$ thuộc $AD$ sao cho $KH\perp HA$. $HB,HC$ cắt $(HKD)$ tại $M,N$ khác $H$. $DN,DM$ cắt $CA,AB$ tại $E,F$. Chứng minh rằng bốn điểm $A,E,H,F$ thuộc một đường tròn.

 

Bài tập tập huấn đội IMO 2016.

[QuangDuong12011998]

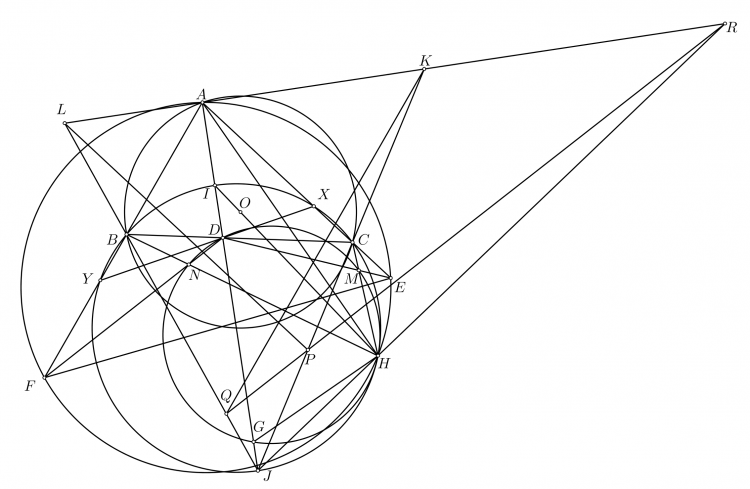
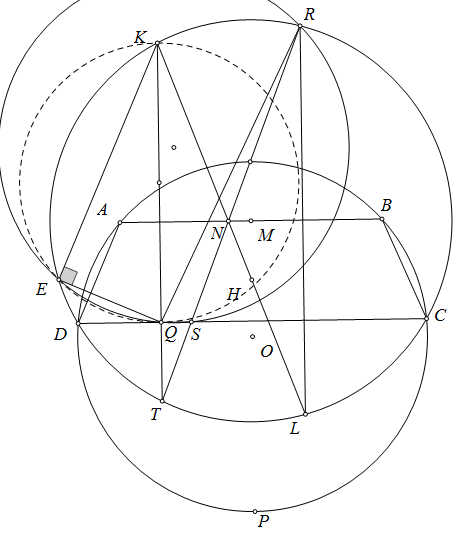
Hic, bài 78 này rối quá ạ.

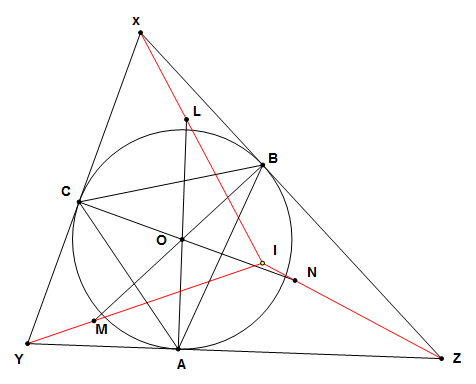
Em đóng góp ĐÚNG 1 BƯỚC để làm đơn giản đi một tí, đó là chỉ ra $R$, $I_a$, $H$ thẳng hàng, nói cách khác là $RI_a$ vuông góc $OI$.

Nhưng nếu lấy $A'$, $B'$, $C'$ lần lượt là chân các phân giác ngoài góc $A$, $B$, $C$ thì $OI\perp \overline{A'B'C'}$. Do vậy có thể đưa về chứng minh $RI_a$ song song $\overline{A'B'C'}$, mà hướng đi này có vẻ khả thi hơn hướng chứng minh vuông góc.

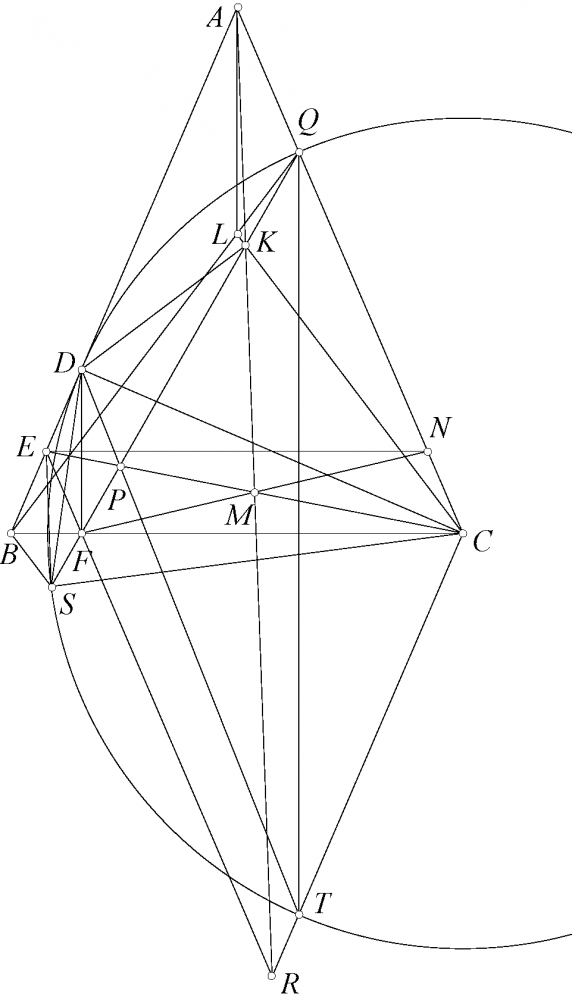
Ý nhỏ này có thể tổng quát: $\triangle ABC$ và một điểm $P$ bất kì $PA$, $PB$, $PC$ cắt $BC$, $CA$, $AB$ tại $D$, $E$, $F$. $EF$, $FD$, $DE$ cắt $BC$, $CA$, $AB$ tại $A'$, $B'$, $C'$. $Y$, $Z$ thuộc $CA$, $AB$ sao cho $BY$, $CZ$ lần lượt song song $DE$, $DF$. $YZ$ cắt $BC$ tại $R$ thì $AR$ song song $\overline{A'B'C'}$.

Để chứng minh $AR$ song song $\overline{A'B'C'}$ thì ta cần có được $(AA',AR,AB,AC)=\dfrac{\overline{A'C'}}{\overline{A'B'}}$.

Đến đây thì chỉ cần áp dụng các định lý Thales, Menelaus @@

Để cho tiện trong việc biểu diễn các tỉ số, có thể giả sử $x\overrightarrow{PA}+y\overrightarrow{PB}+z\overrightarrow{PC}=\overrightarrow{0}$.

Như vậy thì $\dfrac{\overline{DB}}{\overline{DC}}=-\dfrac{z}{y}$, $\dfrac{\overline{EC}}{\overline{EA}}=-\dfrac{x}{z}$, $\dfrac{\overline{FA}}{\overline{FB}}=-\dfrac{y}{x}$.

\[(AA',AR,AB,AC)=(A',R,B,C)=\dfrac{\overline{A'B}}{\overline{A'C}}\cdot\dfrac{\overline{RC}}{\overline{RB}}=\dfrac{z}{y}\cdot\dfrac{\overline{RC}}{\overline{RB}}\]

Theo Menelaus

\[\dfrac{\overline{RC}}{\overline{RB}}=\dfrac{\overline{YC}}{\overline{YA}}\cdot\dfrac{\overline{ZA}}{\overline{ZB}}\]

\[\dfrac{\overline{CY}}{\overline{CA}}=\dfrac{\overline{CY}}{\overline{CE}}\cdot\dfrac{\overline{CE}}{\overline{CA}}=\dfrac{\overline{CB}}{\overline{CD}}\cdot\dfrac{\overline{CE}}{\overline{CA}}=\dfrac{y+z}{y}\cdot\dfrac{x}{z+x}\]

\[\Rightarrow \dfrac{\overline{YA}}{\overline{YC}}=\dfrac{z(x-y)}{x(y+z)}\]

Tương tự $\dfrac{\overline{ZA}}{\overline{ZB}}=\dfrac{y(x-z)}{x(y+z)}$

\[\Longrightarrow \dfrac{\overline{RC}}{\overline{RB}}=\dfrac{y(x-z)}{z(x-y)}\Longrightarrow (A',R,B,C)=\dfrac{x-z}{x-y}\]

\[\dfrac{\overline{A'C'}}{\overline{A'B'}}=\dfrac{\overline{BC'}}{\overline{BA}}\cdot\dfrac{\overline{CA}}{\overline{CB'}}=\dfrac{x}{x-y}\cdot\dfrac{x-z}{x}=\dfrac{x-z}{x-y}=(A',R,B,C)\]

Kết thúc

__________________________________

Quay lại bài toán cũ, vậy là đã chỉ ra được $R$, $I_a$, $H$ thẳng hàng, nên $H$ có thể xác định đơn giản là hình chiếu vuông góc của $I_a$ lên $OI$.

Hình gửi kèm

• 

Bài viết đã được chỉnh sửa nội dung bởi QuangDuong12011998: 11-07-2016 - 10:32

[baopbc]

Tiếp nối lời giải $\boxed{\text{bài 78}}$. (Ta thay điểm $K$ bởi $G$ vì bị trùng lặp)

$\textbf{Lời giải.}$ Gọi $J$ là tâm đường tròn bàng tiếp $\angle A$.Theo lời giải trên dễ thấy $R,H,J$ thẳng hàng do đó $H$ thuộc đường tròn đường kính $IJ$. Do $(AFIJ)=-1$ nên $HI$ là phân giác $\angle AHD$ suy ra $\angle IDH=\angle AHI=\angle JHG$ do đó $HD,HG$ đẳng giác trong $\angle IHJ$.Vậy đường tròn $(DHG)$ tiếp xúc $(JBC)$.

 

 Gọi $X,Y$ lần lượt là giao điểm của đường tròn đường kính $IJ$ với $CA,AB$. Dễ thấy $X,D,Y$ thẳng hàng. Do đường tròn $(HMN)$ tiếp xúc đường tròn $(HBC)$ nên $MN\parallel BC$. Do đó $\angle EDH=\angle MNH=\angle CBH=\angle HXC$ suy ra tứ giác $DXEH$ nội tiếp. Tương tự thì tứ giác $DYFH$ nội tiếp. Ta suy ra $\angle EHF=\angle EHD+\angle FHD=\angle DXA+\angle DYA=180^\circ-\angle BAC$ do đó tứ giác $AEHF$ nội tiếp. $\square$

PS.

Bài này là một hệ quả của bài toán tổng quát Turkey TST 2016

 

Đề nghị bài toán mới.

$\boxed{\text{Bài toán 79}}$ (AoPS) Cho tam giác $ABC$ nội tiếp đường tròn $(O)$ và $H$ là hình chiếu của $A$ lên $BC.P$ là một điểm trong tam giác sao cho $\angle PBA=\angle PCA.Q$ là một điểm trên $(O)$ sao cho $\angle AQP=90^\circ$. Phân giác trong các góc $\angle QBP,\angle QCP$ cắt nhau tại $D$. Các điểm $K,L$ lần lượt trên $AB,AC$ sao cho $HK\perp BD,HL\perp CD$. Các điểm $M,N$ trên $CA,AB$ sao cho $KM\parallel BP,LN\parallel CP$.Chứng minh rằng $(AMN)$ tiếp xúc $(BCD)$

Bài viết đã được chỉnh sửa nội dung bởi baopbc: 11-07-2016 - 12:18

[quanghung86]

Đúng rồi cám ơn Dương, Bảo, điểm $K$ bị lặp, bài này là combine bài Turkey 2016 và CHKMO 2014 !

 

Ý chứng minh của Dương chính là bài CHKMO 2014 ở link. Mấu chốt là dựng ra tâm bàng tiếp $J$ vào sau đó chứng minh $H$ nằm trên $(JBC)$.

 

Nhân bài cũ của Bảo

 

Đễ xuất bài toán tiếp theo.

$\boxed{\text{Bài toán 77}}$ Cho tam giác $ABC$ nội tiếp đường tròn $(O)$. Giả sử $\triangle XYZ$ là tam giác tạo bởi các tiếp tuyến tại $A,B,C.AD,BE,CF$ lần lượt là đường kính của đường tròn $(O).P,Q,R$ theo thứ tự là trung điểm $AX,BY,CZ$. Chứng minh rằng $DP,EQ,FR$ đồng quy.

Nguồn

mjuk ~ Croatia

 

 

Thầy đề nghị thêm 1 ý là

 

b) Cmr đẳng giác của điểm đồng quy trong tam giác $DEF$ nằm trên đường thẳng Euler của tam giác $ABC$.

Bài viết đã được chỉnh sửa nội dung bởi quanghung86: 11-07-2016 - 12:22

[Nguyen Dinh Hoang]

Mấy hôm rồi bận quá hôm nay mới trở lại ddth

$\boxed{\text{Lời giải bài toán 79}}$

Gọi $F$, $X$ lần lượt là giao của $PC$, $PB$ với $AB$, $AC$ thì $FXCB$ nội tiếp và 2 tam giác $QBF$ và $QCX$ đồng dạng nên $\frac{QB}{QC} = \frac{BF}{CX} =\frac{BP}{PC}$ nên $D$ nằm trên $FXBC$.

Ta lại có $\angle KML = \angle BXC = 180^{\circ} - \angle KHL$ nên $K, L, M,N, H$ đồng viên 

Gọi $E$ là giao của $(NBH)$ với $(MCH)$ ta có $\angle BEH + \angle HEC = \angle BNH + \angle HMC = \angle KHB + \angle LHC = \angle BDC$ nên $E$ nằm trên $(BCD)$. Đến đây có lẽ phải sử dụng lượng giác một chút

$\frac{sin HEC}{sinBEH}. \frac{BH}{CH} = \frac{BE}{CE} = \frac{sinLHC}{sinKHB}. \frac{BH}{CH}$.

$I$ là giao của $AQ$ với $BC$, $J$ là giao của $ID$ với $(DBC)$. Ta cũng chứng minh được $\frac{JB}{JC} = \frac{BH}{CH}.\frac{sinLHC}{sinKHB}$ vì có góc vuông  nên $J$ trùng $E$ Lại áp dụng định lý $Miquel$ Ta có $E$ nằm trên $(AMN)$. Gọi $Ex$ là tiếp tuyến của $(ANM)$ thì $Ex$ đi qua trung điểm của $AI$ nên $\angle xEI = \angle AIE = \angle DBE$ nên $Ex$ cũng là tiếp tuyến của $(DBC)$. Ta có điều phải chứng minh.

Hình gửi kèm

• 

Bài viết đã được chỉnh sửa nội dung bởi baopbc: 13-07-2016 - 23:32
$\LaTeX$ + hình rối quá, Hoàng sửa lại được không?

[baopbc]

Đề xuất bài toán mới để tiếp tục topic.

 

$\boxed{\text{Bài toán 80}}$ (AoPS) Cho hình thang cân $ABCD$ nội tiếp đường tròn $\Omega$ với $AB\parallel CD.M$ là trung điểm $AB$ và $P$ là điểm chính giữa cung $CD$ không chứa $A$ của $\Omega$. Gọi $H$ là trực tâm tam giác $PAB$ và $(M)$ là đường tròn tâm $M$ đi qua $C,D.N$ là một điểm trên đoạn $AB$ ($N$ khác $A,B$ và $M$). Đường thẳng $HN$ cắt $(M)$ tại $K,L$ sao cho $L$ nằm trong $\Omega$. Chọn hai điểm $Q,R$ theo thứ tự thuộc $CD$ và $(M)$ sao cho $KQ,LR$ cùng vuông góc với $AB$. Gọi $RN$ cắt $CD$ tại $S$. Đường tròn ngoại tiếp tam giác $QRS$ cắt lại $(M)$ tại $E$. Chọn $F$ trên $ER$ sao cho $KF\perp KL$. Chứng minh rằng đường tròn ngoại tiếp tam giác $KEF$ tiếp xúc $\Omega$

 

Bài viết đã được chỉnh sửa nội dung bởi baopbc: 19-07-2016 - 20:35

[baopbc]

$\boxed{\text{Bài toán 80}}$ đã lâu chưa có lời giải nên mình sẽ đưa ra lời giải để tiếp tục topic.

$\boxed{\text{Lời giải bài toán 80}}$.

Hình 1.

Đầu tiên ta sẽ chứng minh $\angle KEQ=90^\circ$. Biến đổi góc : $\angle REQ=180^\circ-\angle RSQ=\angle RNB=\angle LNB,\ \angle KER=\angle KLR$. Chú ý $RL\perp AB$ nên $\angle KEQ=\angle REQ+\angle KER=90^\circ$. Từ đó $E\equiv (KQ)\cap (M).$

Hình 2.

Do $AB$ đi qua tâm $M$ của $(M)$ nên dễ thấy $RN$ cắt $KQ$ tại $T$. Gọi $S$ là điểm chính giữa cung $AB$ không chứa $CD$ của $\Omega$. Chú ý trực tâm $H$ đối xứng với $S$ qua $AB$ nên $TR$ đi qua $S$. Tiếp theo ta sẽ chứng minh $QS$ đi qua $F$. Gọi $Z,G$ lần lượt là giao điểm của $KF$ và $EQ$ với $(M)$. Chú ý rằng $M$ là trung điểm $HS,HK\perp KZ$ nên $\angle KZS=90^\circ$. Từ đó $ZS$ đi qua $G$. Từ đây theo định lí $Pascal$ thì $F,S,Q$ thẳng hàng.

 

Gọi $QS$ cắt đường tròn $(KEF)$ tại $X$. Do $\angle KXF=\angle KER=\angle KTR$ từ đó tứ giác $KSTX$ nội tiếp suy ra $QX.QS=QT.QK=QD.QC$ kéo theo tứ giác $SCXB$ nội tiếp. 

 

Do tứ giác $KHST$ nội tiếp nên năm điểm $K,H,S,T,X$ cùng thuộc một đường tròn. Từ đó $\angle FKX=90^\circ+\angle HKX=90^\circ+\angle HSX=\angle XDS$. Từ đó $(KEF)$ tiếp xúc đường tròn $\Omega. \ \blacksquare$

 

Việc đề xuất bài toán mới thì thầy có thể giúp đỡ được không ạ?

Nguồn gốc bài toán: http://www.artofprob...1202245p5915727

PS. Thành thật xin lỗi vì việc trùng điểm $S$ nên mình phải vẽ ra hai hình cho tiện!

Bài viết đã được chỉnh sửa nội dung bởi baopbc: 20-07-2016 - 18:01
Up nguồn

[halloffame]

$\boxed{\text{Bài toán 81}}$ Cho tam giác $ABC,$ phân giác $BD,CE$ và tâm nội tiếp $I.$ Chứng minh $AI$ đi qua tâm đường tròn Euler của tam giác $IDE.$

chờ thầy post mà lâu quá   

Bài viết đã được chỉnh sửa nội dung bởi halloffame: 20-07-2016 - 22:59

[QuangDuong12011998]

Bài 81 này có phát biểu trông rất lạ.

Lời giải bài 81(hơi phức tạp, hi vọng có lời giải đơn giản hơn)

Gọi $I_a$, $I_b$, $I_c$ là tâm bàng tiếp góc $A,B,C$ của $\triangle ABC$.

Ta có $\overline{II_a}\cdot\overline{IA}=\overline{II_b}\cdot\overline{IB}=\overline{II_c}\cdot\overline{IC}=k$.

Xét phép nghịch đảo cực $I$, phương tích $k$ là $I^k_I$.

\[I^k_I: D,E\mapsto\text{đối xứng của $I_b$, $I_c$ qua $B$, $C$}\]

Có điều này do $I^k_I$ biến $AC$ thành $(II_cI_a)$  nên nó biến $D$ thành giao điểm khác $I$ của $IB$ với $(II_aI_c)$ - chính là đối xứng của $I_b$ qua $B$.

Gọi điểm đối xứng với $I_b$, $I_c$ qua $B$, $C$ là $B'$, $C'$. Như vậy cần phải chứng minh $IA$ đi qua điểm Kosnita của $\triangle IB'C'$ (điểm Kosnita là điểm đẳng giác của tâm đường tròn 9 điểm). Gọi $X$ là tiếp điểm của $(I)$ với $BC$, ta đã quen thuộc với tính chất $IA$ đi qua tâm ngoại tiếp $\triangle IBC$ nên $IA$, $IX$ đẳng giác với góc $(IB',IC')$.

Do vậy ta sẽ chứng minh $IX$ đi qua tâm đường tròn chín điểm của $\triangle IB'C'$.

Cấu hình có vẻ vẫn chưa đủ liên kết để giải quyết.

Ý tưởng của mình xuất phát từ việc để ý tới chỗ này: $B$, $C$ là trung điểm $I_bB'$, $I_cC'$. $I_bB'$, $I_cC'$ cắt nhau tại $I$, ta sẽ có tâm của $(IBC)$ là trung điểm của đoạn nối tâm $(IB'C')$ và $(II_bI_c)$(chúng đồng trục, rút ra từ tỉ số phương tích) và hệ quả là trực tâm $\triangle IBC$ là trung điểm của đoạn nối trực tâm $\triangle IB'C'$ và $\triangle II_bI_c$.

Kí hiệu $H_1$, $O_1$, $N_1$ là trực tâm, tâm ngoại tiếp, tâm đường tròn chín điểm của $\triangle IB'C'$.

$H_2$, $O_2$, $N_2$  là trực tâm, tâm ngoại tiếp, tâm đường tròn chín điểm của $\triangle IBC$.

$H_3$, $O_3$, $N_3$  là trực tâm, tâm ngoại tiếp, tâm đường tròn chín điểm của $\triangle II_bI_c$

Cần chỉ ra $N_1$ thuộc $IX$, hay $IH_2$ là xong.

$H_3$ chính là $I_a$ và $N_3$ chính là $O$. Theo định lý ERIQ thì $N_1$ là đối xứng của $O$ qua $N_2$.

Đến đây mọi thứ đã quá rõ ràng: $\triangle IBC$, $O$ thuộc trung trực $BC$. $N_2$ là tâm đường tròn chín điểm của $\triangle IBC$. Đối xứng của $O$ qua $N_2$ thuộc đường cao ứng với $I$ của $\triangle IBC$.

Điều này là rõ ràng bởi đường cao ứng với $I$ và trung trực của $BC$ đối xứng nhau qua tâm đường tròn chín điểm của $\triangle IBC$.

Hình gửi kèm

• 

Bài viết đã được chỉnh sửa nội dung bởi QuangDuong12011998: 21-07-2016 - 14:38

[baopbc]

$\boxed{\text{Lời giải khác cho bài toán 81}}$.

Gọi $O,H,N$ lần lượt là trực tâm, tâm ngoại tiếp và tâm đường tròn $Euler$ của tam giác $IED$. Gọi $O'$ là đối xứng của $O$ qua $DE$ thì $OO'=IH$. Từ đó $IHO'O$ là hình bình hành suy ra $AO'$ đi qua $N$ là trung điểm $OH$. Do đó ta chỉ cần chứng minh $AI$ đi qua $O'$ là đối xứng của $O$ qua $DE$ đồng thời là tâm đường tròn ngoại tiếp tam giác $HED$. Đường thẳng qua $D,E$ lần lượt song song với $CI,BI$ cắt nhau tại $P$ thì tứ giác $PDEH$ nội tiếp. Gọi $(O')$ cắt $AC,AB$ tại $M,N$. Do $\angle AEM=\angle PDM+\angle AEP=\angle B/2+\angle C/2=180^\circ-\angle BIC=180^\circ-\angle EPD=180^\circ-\angle EMD$ nên từ đó $EMND$ là hình thang cân suy ra $AI$ đi qua tâm $(EMND)$ hay $AI$ đi qua $O'.\ \blacksquare$

 

PS. Anh Dương đề xuất bài toán mới đi ạ!

Bài viết đã được chỉnh sửa nội dung bởi baopbc: 21-07-2016 - 17:36

[QuangDuong12011998]

Mình đề nghị bài mới.

Bài sau được đặc biệt hóa từ kết quả mình chế (bài tổng quát thì không sơ cấp tí nào).

$\boxed{\text{Bài toán 82}}$ $O$ là tâm đường tròn ngoại tiếp tam giác $ABC$. Dựng ra ngoài tam giác $ABC$ các tam giác đều $DBC$, $ECA$, $FAB$.

Chứng minh rằng các đường tròn $(OAD)$, $(OBE)$, $(OCF)$ còn một điểm chung khác $O$.

[baopbc]

$\boxed{\text{Lời giải bài toán 82}}$. Bài này khá đơn giản!

Gọi $X,Y,Z$ lần lượt là giao điểm của $(AOX)(BOY)(COZ)$ với $(O)$. Do tứ giác $AOXD$ nội tiếp nên $\angle ADX=180^\circ-\angle AOX=2\angle OAX=2\angle ODX$. Từ đó $DA,DX$ đẳng giác trong $\angle BDC$. Chú ý tam giác $BDC$ đều nên từ đó $AD,AX$ đẳng giác trong $\angle A$. Theo định lí $Napoleon$ thì $AX,BY,CZ$ đồng quy tại điểm đẳng giác với điểm $Napoleon$ của tam giác $ABC$. Gọi điểm đó là $K$.

 

Gọi $OK$ cắt $(AOX)$ tại $T$ thì $OA^2=OK.OT$ từ đó $T$ xác định duy nhất trên $OK$. Mặt khác do $OA=OB=OC$ nên ba đường tròn $(AOX)(BOY)(COZ)$ đồng quy tại $T.\blacksquare$

 

PS. Kết quả về ba đường tròn đồng quy dạng này thì khá nhiều và quen thuộc với các chứng minh hoàn toàn tương tự như trên. 

Một kết quả khác như sau. Cho tam giác $ABC$ nội tiếp đường tròn $(O)$. Gọi $X,Y,Z$ lần lượt là đối xứng của $A,B,C$ qua $BC,CA,AB$. Khi đó $(AOX)(BOY)(COZ)$ đồng quy.

Chứng minh hoàn toán tương tự như trên, chú ý điểm cần tìm ở đây là điểm $Konista$ của tam giác $ABC$.

 

Đề xuất bài toán tiếp theo khá nhẹ nhàng!

$\boxed{\text{Bài toán 83}}$.(AoPS) Cho tam giác $ABC$, trực tâm $H.M$ là trung điểm $BC$. Trên $BC$ lấy $S$ sao cho $HS,HM$ đẳng giác. Hạ $AP\perp HS$. Chứng minh rằng $(MSP)$ tiếp xúc $(ABC)$.

 

[quanghung86]

Bài toán 83 của Bảo có thể coi là trường hợp riêng của bài sau (sau khi viết lại cho tam giác $PBC$)

 

http://analgeomatica...2-thang-12.html

 

Thầy thử đề xuất một bài mới !

$\boxed{\text{Bài toán 84.}}$ Cho tam giác $ABC$ có đường cao $AD$. Trên tia $BC,CB$ lấy các điểm $G,H$ sao cho $BG=BA,CH=CA$. $E,F$ là trung điểm của $DG,DH$. Đường tròn $(A,AD)$ cắt $CA,AB$ tại $P,Q$. $M,N,Y,Z$ lần lượt đối xứng $A$ qua $C,B,P,Q$. $NE$ cắt đường tròn $(A,AD)$ tại $K$ sao cho $K,N$ khác phía đường thẳng qua $A$ vuông góc $KN$. $MF$ cắt đường tròn $(A,AD)$ tại $L$ sao cho $L,M$ khác phía đường thẳng qua $A$ vuông góc $LM$. Lấy $S,T$ thuộc $MF,NE$ sao cho $YS\parallel PL$ và $ZT\parallel QK$. Chứng minh rằng $D$ là tâm $(AST)$.

 

Hình gửi kèm

• 

[QuangDuong12011998]

$\boxed{\text{Lời giải bài toán 82}}$. Bài này khá đơn giản!

Gọi $X,Y,Z$ lần lượt là giao điểm của $(AOX)(BOY)(COZ)$ với $(O)$. Do tứ giác $AOXD$ nội tiếp nên $\angle ADX=180^\circ-\angle AOX=2\angle OAX=2\angle ODX$. Từ đó $DA,DX$ đẳng giác trong $\angle BDC$. Chú ý tam giác $BDC$ đều nên từ đó $AD,AX$ đẳng giác trong $\angle A$. Theo định lí $Napoleon$ thì $AX,BY,CZ$ đồng quy tại điểm đẳng giác với điểm $Napoleon$ của tam giác $ABC$. Gọi điểm đó là $K$.

 

Gọi $OK$ cắt $(AOX)$ tại $T$ thì $OA^2=OK.OT$ từ đó $T$ xác định duy nhất trên $OK$. Mặt khác do $OA=OB=OC$ nên ba đường tròn $(AOX)(BOY)(COZ)$ đồng quy tại $T.\blacksquare$

 

PS. Kết quả về ba đường tròn đồng quy dạng này thì khá nhiều và quen thuộc với các chứng minh hoàn toàn tương tự như trên. 

Một kết quả khác như sau. Cho tam giác $ABC$ nội tiếp đường tròn $(O)$. Gọi $X,Y,Z$ lần lượt là đối xứng của $A,B,C$ qua $BC,CA,AB$. Khi đó $(AOX)(BOY)(COZ)$ đồng quy.

Chứng minh hoàn toán tương tự như trên, chú ý điểm cần tìm ở đây là điểm $Konista$ của tam giác $ABC$.

Bảo chỉ chưa đúng tên gọi thôi.

Điểm Napoleon thì khác(không có trong bài này): dựng ra ngoài các tam giác $A'BC$, $B'CA$, $C'AB$ cân tại  $A'$, $B'$, $C'$ và có góc ở đáy bằng 30 độ thì $AA'$, $BB'$, $CC'$ đồng quy tại điểm Napoleon.

$AD$, $BE$, $CF$ đồng quy tại điểm Fermat thứ nhất ($X_{13}$). $AX$, $AD$ đẳng giác, $AX$ đi qua đẳng giác của điểm Fermat. Đẳng giác của điểm Fermat thứ nhất là điểm isodynamic thứ nhất (một trong hai giao điểm của 3 đường tròn Apollonius) và điểm này là $X_{15}$, tên tại ETC(Encyclopedia of Triangle Centers).

Như vậy là điểm $K$ và điểm $T$ như Bảo đề cập trong chứng minh chính lần lượt là hai điểm isodynamic thứ nhất và thứ hai $(X_{15},X_{16})$.

Trường hợp lấy đối xứng qua ba cạnh tam giác thì ta được định lý Musselman, giao điểm của ba đường tròn là tâm ngoại tiếp và nghịch đảo của điểm Kosnita $(X_{54})$ qua đường tròn ngoại tiếp - điểm này là $X_{1157}$.

Một trong các cách tổng quát: $P$ là điểm thỏa mãn $PQ$ song song với đường thẳng Euler ($Q$ là đẳng giác của $P$). $PA$, $PB$, $PC$ cắt $(PBC)$, $(PCA)$, $(PAB)$ tại $D$, $E$, $F$ thì $(OAD)$, $(OBE)$, $(OCF)$ đồng trục.

[quanghung86]

Bổ đề. Cho tam giác $ABC$ cân tại $A$ có đường cao $CD$. Gọi $E$ là trung điểm của $BD$, $M$ là trung điểm $CE$, phân giác của $\angle{BDC}$ cắt $CE$ tại $P$. Đường tròn tâm $C$ bán kính $CD$ cắt $AC$ tại $Q$. Gọi $K$ là giao điểm của $PQ$ và $AM$.

 

a) (Bài T12/465 THTT) Chứng minh rằng tam giác $CKD$ vuông.

 

b) Lấy $S$ thuộc $PF$ sao cho $ES\parallel AM$. Chứng minh rằng $CS=CD$.

 

 

Chứng minh. a) (Của Nguyễn Đức Bảo) Gọi $T$ là giao của $DP$ với đường tòn tâm $C$ bán kính $CD$. Do $DT$ là phân giác $\angle{CDE}$ và $BD$ là tiếp tuyến của đường tròn tâm $(C)$ nên $\angle{DCT}=2\angle DBT=90^\circ $ nên  $CT \perp DC$. Lại có tam giác $CDQ$ cân tại $C$ nên ta có biến đổi góc $\angle CQT=\angle{DQC}-45^\circ=90^\circ-\frac{\angle{DCQ}}{2}-45^\circ=45^\circ+\frac{90^\circ-\angle{BAC}}{2}=90^\circ -\angle{ACB}$ do đó $QT \perp BC$. Gọi $F$ là hình chiếu của $D$ lên $BC$ khi đó tam giác $DEF$ và tam giác $TCQ$ có các cạnh tương ứng song song nên $DT,FQ$ và $CE$ đồng quy tại $P$. Mặt khác do $EF\parallel AC$ nên nếu $N$ là đối xứng của $F$ qua $M$ thì $N$ thuộc $AC$. Áp dụng định lí Menelaus cho tam giác $QFN$ với $M,K,A$ thẳng hàng, ta thu được $\frac{KQ}{KF}.\frac{AN}{AQ}.\frac{MF}{MN}=1$ từ đó $\frac{KQ}{KF}=\frac{AQ}{AN}$. Gọi $BQ$ cắt $CK$ tại $L$. Áp dụng định lí Menelaus cho tam giác $QBF$ với $L,K,C$ thẳng hàng thì $\frac{LB}{LQ}.\frac{KQ}{KF}.\frac{CF}{CB}=1$ với chú ý $EF\parallel AC$ nên $\frac{CF}{CB}=\frac{AE}{AB}$ và $AN=AE$ ta thu được $\frac{LB}{LQ}=\frac{KF}{KQ}.\frac{CB}{CF}=\frac{AN}{AQ}.\frac{AB}{AE}=\frac{AB}{AQ}$. Từ đó $AL$ là phân giác $\angle QAB$ nên $LB = LC$. Từ đó theo hệ thức lượng trong tam giác vuông thì $CQ^2=CD^2=CF.CB$ suy ra $\angle{FQC}=\angle{QBC}=\angle{LCB}$. Từ đó $\triangle CFQ \sim\triangle KFC$ g.g suy ra $\angle{FKC}=\angle{FCQ}=\angle{DBC}=\angle{FDC}$, vậy $KCFD$ là tứ giác nội tiếp hay $\angle{CKD}=90^\circ$.

 

b) Lấy $R$ đối xứng $A$ qua $M$, do $EF\parallel AC$ nên dễ thấy $R$ nằm trên $EF$. Từ đó $\frac{FS}{FK}=\frac{FE}{FR}=\frac{FB}{FC}$, suy ra $SB\parallel CK$. Từ chứng minh trên ta có $\triangle KFC \sim\triangle CFQ\sim\triangle CQB$. Từ đó $\frac{KF}{KC}=\frac{CQ}{CB}=\frac{CD}{CB}$, suy ra $\frac{KF^2}{KC^2}=\frac{CD^2}{CB^2}=\frac{CF}{CB}=\frac{KF}{KS}$. Từ đó $KC^2=KF.KS$, suy ra $\angle KSC=\angle KCF=\angle CBS$. Từ đó $CS^2=CF.CB=CD^2$. Ta có điều phải chứng minh.

 

Giải bài toán. Gọi $U,V$ là trung điểm của $AS,AT$. Như vậy $U$ thuộc $LP$ để $MF\parallel CU$, áp dụng bài trên vào tam giác cân $CAH$ thì $\angle AUD=90^\circ$. Tương tự $\angle AVD=90^\circ$. Từ đó $DA=DS=DT$.

 

 

$\boxed{\text{Bài toán 85.}}$ Cho tam giác $ABC$ và $P$ cố định. Các điểm $D,E,F$ thay đổi trên đường thẳng $PA,PB,PC$ sao cho $\overline{PA}.\overline{PD}=\overline{PB}.\overline{PE}=\overline{PC}.\overline{PF}$. Chứng minh rằng điểm Lemoine của tam giác $DEF$ luôn thuộc một đường thẳng cố định khi $D,E,F$ di chuyển.