Chủ đề này có 434 trả lời

[huynhtanduyan]

Bài toán 97:

Cho 2 điểm cố định A,B và điểm C di động trên mặt phẳng sao cho ACB^=a (0<a<180) không đổi cho trước. Hình chiếu của tâm đường tròn nội tiếp I của tam giác ABC xuống ba cạnh AB, BC, CA lần lượt là D, E, F. AI và BI cắt EF lần lượt tại M,N. 
a) Chứng minh độ dài MN không đổi.
b) CM đường tròn(DMN) luôn đi qua một điểm cố định.

Bài viết đã được chỉnh sửa nội dung bởi huynhtanduyan: 08-12-2016 - 15:07

[SinCosTan]

Bài 97

Hình gửi kèm

• 

[quanghung86]

Bài toán 98. Cho tam giác $ABC$ giả sử có điểm $P$ nằm trong tam giác sao cho $\angle PBA=\angle PCA$ đồng thời nếu có các đường tròn $(K)$ qua $P,C$ và đường tròn $(L)$ qua $P,B$ sao cho $(K),(L)$ cắt nhau tại $Q$ khác $P$ thì $BQ$ đi qua giao điểm $E$ của $(K)$ và $AC$ còn $CQ$ đi qua giao điểm $F$ của $(L)$ và $AB$. Chứng minh rằng $BE=CF$.

 

 

Nguồn gốc: http://www.cut-the-k.../Stoyanov.shtml

[moonkey01]

Bài toán 98. Cho tam giác $ABC$ giả sử có điểm $P$ nằm trong tam giác sao cho $\angle PBA=\angle PCA$ đồng thời nếu có các đường tròn $(K)$ qua $P,C$ và đường tròn $(L)$ qua $P,B$ sao cho $(K),(L)$ cắt nhau tại $Q$ khác $P$ thì $BQ$ đi qua giao điểm $E$ của $(K)$ và $AC$ còn $CQ$ đi qua giao điểm $F$ của $(L)$ và $AB$. Chứng minh rằng $BE=CF$.

 

Figure4229.png

 

Nguồn gốc: http://www.cut-the-k.../Stoyanov.shtml

 

Lời giải của em như sau:

 

Không mất tính tổng quát, giả sử vị trí các điểm như hình vẽ thì ta có $\angle BFP = \angle BQP = \angle PCA = \angle PBA$ nên $\Delta PBF$ cân tại $P$ hay $PB=PF$. Tương tự ta có $PE=PC$ nên $\Delta PBE=\Delta PFC$ (c.g.c), dẫn đến $BE=CF$.

Bài viết đã được chỉnh sửa nội dung bởi moonkey01: 02-01-2017 - 12:18

[moonkey01]

Em đề nghị bài toán tiếp theo, đã được phát biểu lại cho gọn hơn. Bài toán trích từ đề thi chọn HSG lớp 9 trường THPT chuyên Trần Đại Nghĩa năm ngoái.

 

Bài toán 99: Cho tam giác $ABC$ có $O$ là tâm ngoại tiếp. Đường thẳng $d$ đi qua $O$ sao cho $B,C$ nằm cùng phía với $d$. Gọi $M,N$ là hình chiếu của $B,C$ trên $d$. Đường thẳng qua $M$ vuông góc $CA$ cắt đường thẳng qua $N$ vuông góc $AB$ tại $T$. Chứng minh rằng $T$ luôn thuộc đường tròn cố định khi $d$ thay đổi.

 

Theo cái nhìn chủ quan của em thì đây là một bài toán có cấu hình đẹp và thú vị, nên em rất mong thầy Hùng và các anh chị đóng góp những mở rộng của bài toán trên.

Bài viết đã được chỉnh sửa nội dung bởi moonkey01: 02-01-2017 - 14:32

[quanghung86]

Cám ơn Hoàng đã đóng góp lời giải và bài toán mới.

 

Bài toán này thực chất là một kết quả kinh điển. Chứng minh cực trực giao của một đường thẳng đi qua tâm ngoại tiếp nằm trên đường tròn Euler. Mình xin đưa ra một chứng minh ngắn gọn như sau. Viết bài toán theo ký hiệu điểm.

 

Bài toán. Cho tam giác $ABC$ có tâm ngoại tiếp $O$. $d$ là đường thẳng đi qua $O$. $D,E,F$ là hình chiếu của $A,B,C$ lên $d$. Chứng minh rằng đường thẳng qua $D,E,F$ vuông góc với $BC,CA,AB$ đồng quy trên đường tròn Euler của $ABC$.

 

 

Lời giải. Gọi $l$ là đường thẳng qua trực tâm $H$ của $ABC$ và vuông góc với $d$. Gọi $S$ là điểm anti-Steiner của $l$. $K$ đối xứng $H$ qua $BC$ thì $K$ thuộc $(O)$. Do $S$ là điểm anti-Steiner của $l$ nên $T$ đối xứng $S$ qua $BC$ nằm trên $l$. Từ đó gọi $ST$ cắt $(O)$ tại $X$ khác $S$ thì theo tính đối xứng ta có $\angle AXS=\angle AKS=\angle KHT$ do đó $AX\parallel HT\perp d$ nên $AX$ đi qua $D$ hay $D$ là trung điểm $AX$. Từ đó đường thẳng qua $D$ vuông góc $BC$ đi qua trung điểm $G$ của $SH$. Tương tự các đường thẳng còn lại đi qua $G$ và dễ thấy $G$ nằm trên đường tròn Euler của $ABC$.

 

Bài toán 100. Cho tam giác $ABC$ nội tiếp đường tròn $(O)$, trực tâm $H$. $MN$ và $PQ$ là hai dây cung vuông góc với nhau tại điểm $S$. Gọi giao điểm của đường thẳng Simson ứng với $M,N$ của tam giác $ABC$ là $K$. Gọi giao điểm của đường thẳng Simson ứng với $P,Q$ của tam giác $ABC$ là $L$. Chứng minh rằng $K,L$ đối xứng nhau qua trung điểm $T$ của $HS$.

 

 

 

 

[quanghung86]

Như vậy VMF's Marathon Hình học Olympic đã đạt tới 100 bài. Trong giai đoạn cuối thi VMO và vòng 2 thì topic này khá thiết thực. Do đó mình xin thay đổi một chút nội quy cho VMF's Marathon Hình học Olympic sôi động hơn.

 

- Đánh số bài bôi đen theo thứ tự liên tục.

 

- Người giải xong thì nên đề nghị một bài toán nếu lấy ở đề thi hoặc AoPS hoặc các nguồn trên mạng thì kèm trích dẫn. Có thể nhờ người đề nghị.

 

- Một bài để không quá 2 ngày, nếu đủ 2 ngày mà không ai giải thì người đề nghị có thể post đáp án. Nếu quá 2 ngày người đề nghị không post đáp án thì tôi hoặc BQT sẽ xóa bài đó và thay vào đó đề nghị khác có đáp án cẩn thận vào chính số thứ tự đó.

 

- Nên viết lời giải kèm hình vẽ và không dẫn link giải. Người giải viết lại lời giải tiếng Việt nếu tham khảo ở link nào đó và dẫn lại link tham khảo cuối bài giải.

 

Hy vọng thời gian tới mình đủ sức tuyển tập và biên tập các bài toán ở topic này thành một Ebook hình học của VMF. Chúc các bạn mọi việc may mắn và topic sẽ lại được các bạn tham gia nhiệt tình.

 

Trân trọng.

 

Trần Quang Hùng.

Bài viết đã được chỉnh sửa nội dung bởi halloffame: 30-12-2017 - 14:12

[quanghung86]

Mình có post một tổng quát cho tính chất của bài toán 99. tại đây http://artofproblems...h498545p2801321 đã lâu, đó là một mở rộng sang conic, lời giải của Luis hay nhưng cũng phức tạp. Mở rộng này không gần gũi với toán Olympic lắm vậy hãy chỉ để tham khảo.

Bài viết đã được chỉnh sửa nội dung bởi halloffame: 30-12-2017 - 14:12

[QuangDuong12011998]

Lâu lắm rồi em không đăng gì :3 

Lời giải của em kiểu biến hình.

Để đến được kết luận thì em sử dụng các kết quả sau.

Định nghĩa cực trực giao. Cho trước tam giác $ABC$ và đường thẳng $\ell$. Lấy $D$, $E$, $F$ là hình chiếu vuông góc của $\ell$ lên $BC$, $CA$, $AB$.

Khi đó các đường thẳng qua  $D$, $E$, $F$ và lần lượt vuông góc với  $BC$, $CA$, $AB$ đồng quy tại một điểm được gọi là cực trực giao của $\ell$ với tam giác $ABC$.

Nhận xét. Từ định nghĩa cực trực giao, ta có được một chú ý như sau: nếu $\ell$ bị tịnh tiến thành $\ell'$ theo một vector $\overrightarrow{v}$ vuông góc với $\ell $ thì $\overrightarrow{TT'}=\overrightarrow{v}$. Trong đó $T$, $T'$ là cực trực giao của $\ell$, $\ell'$.

Định lý 1. $MN$ là một dây của đường tròn ngoại tiếp tam giác $ABC$ thì cực trực giao của $MN$ với tam giác $ABC$ chính là giao điểm của đường thẳng Simson của $M$ và $N$ với tam giác $ABC$.

Định lý 2. $\ell$ là một đường kính của đường tròn ngoại tiếp tam giác $ABC$. $A'$, $B'$, $C'$ là trung điểm $BC$, $CA$, $AB$ thì cực trực giao của $\ell$ với tam giác $ABC$ là điểm Anti-Steiner của $\ell$ với tam giác $A'B'C'$(bởi vì tâm ngoại tiếp $O$ của tam giác $ABC$ chính là trực tâm của tam giác $A'B'C'$)

----------------------------------

Định lý 2 là một bước trong chứng minh định lý Fontene thứ nhất. Trong file đính kèm(epsilon số 7), bài viết "Đường thẳng Simson" thì định lý 1 được đánh số 11(thực ra định lý 11 là một phát biểu tương đương). Còn định lý 2 có thể tham khảo bài viết(trong file đính kèm).

_______________________________________________________________

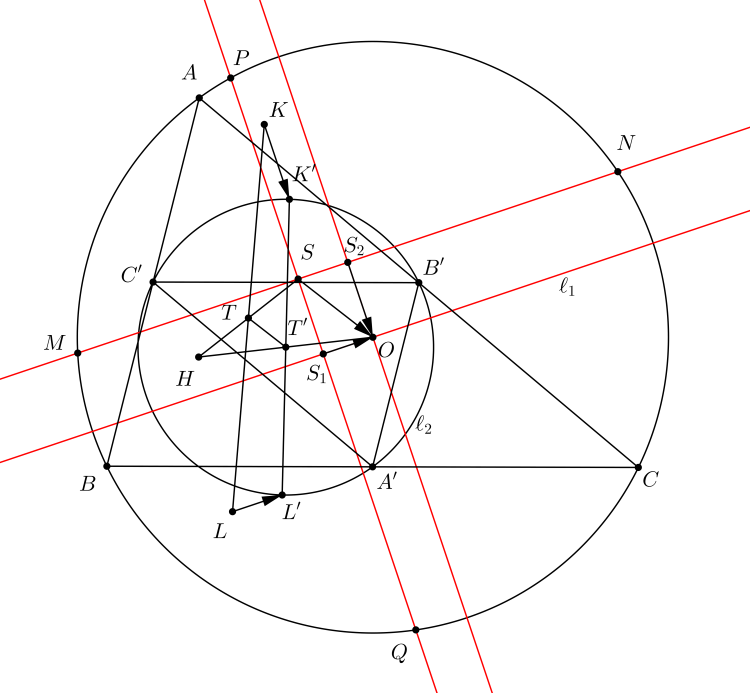
Quay trở lại bài toán ban đầu. Ta tịnh tiến $MN$ thành đường kính $\ell_1$, tịnh tiến $PQ$ thành đường kính $\ell_2$.

Gọi $S_1$, $S_2$ là hình chiếu vuông góc của $O$ lên $PQ$, $MN$.

Gọi $K'$, $L'$ là cực trực giao của $\ell_1$, $\ell_2$ với tam giác $ABC$.

Theo nhận xét từ đầu post:

\[\overrightarrow{KK'}=\overrightarrow{S_2O}\qquad \overrightarrow{LL'}=\overrightarrow{S_1O}\]

Gọi $T$, $T'$ là trung điểm $KL$ và $K'L'$.

Theo định lý 2, $K'$, $L'$ là điểm Anti-Steiner của $\ell_1$, $\ell_2$ với tam giác $A'B'C'$, mà chúng lại vuông góc nên $K'L'$ là đường kính của đường tròn chín điểm. Nghĩa là $T'$ chính là tâm đường tròn chín điểm, tức là trung điểm của $OH$.

\[2\overrightarrow{TT'}=\overrightarrow{KK'}+\overrightarrow{LL'}=\overrightarrow{S_2O}+\overrightarrow{S_1O}=\overrightarrow{SO}\]

Điều này chứng tỏ rằng $T$ là trung điểm $HS$.

_______________________________________________________________

Cuối cùng, em muốn nhờ thầy đề nghị bài toán mới.

Hình gửi kèm

• 

File gửi kèm

•  Intersections_of_nine_point_circle__pedal_circle_and_cevian_circle.pdf   527.51K   774 Số lần tải
•  epsilon_vol7_2016_full.pdf   7.08MB   29 Số lần tải

Bài viết đã được chỉnh sửa nội dung bởi QuangDuong12011998: 03-01-2017 - 11:07

[quanghung86]

Do sơ suất mình đã đề nghị trùng bài toán 36, cám ơn Hoàng đã cho lời giải mới cho bài đó. Cám ơn Dương đã đóng góp lời giải, mình xin đề xuất lại đề toán 101.

 

Bài toán 101. Cho tam giác $ABC$ với đường cao $AH$. $M,N$ thuộc $BC$ sao cho $AM\perp AB, AN\perp AC$. $I$ là tâm nội tiếp tam giác $AMN$. $NI,MI$ cắt $CA,AB$ lần lượt tại $E,F$. Gọi $K,L$ là tâm nội tiếp tam giác $AHM,AHN$. Chứng minh rằng $EK,FL$ và $IH$ đồng quy.

[quanghung86]

Đáp án bài toán 100.

 

Trong suốt bài toán này nếu $X$ là một điểm nằm trên đường tròn ngoại tiếp tam giác $ABC$ thì ta ký hiệu $s_X$ chỉ đường thẳng Simson của $X$ ứng với tam giác $ABC$. Ta sử dụng các bổ đề sau

 

Bổ đề 1. Cho tam giác $ABC$ nội tiếp đường tròn $(O)$ và $M,N$ thuộc $(O)$ thì $(s_M,s_N)=\frac{1}{2}(\overrightarrow{ON},\overrightarrow{OM})(\bmod\pi)$.
 

Bổ đề 2. Cho tam giác $ABC$ nội tiếp đường tròn $(O)$ và trực tâm $H$ và $P$ là một điểm bất kỳ trên $(O)$ thì $s_P$ đi qua trung điểm $PH$.
 

Hai bổ đề là các bài toán cơ bản xin không nêu cách chứng minh.

 

Bổ đề 3. Cho tam giác $ABC$ nội tiếp đường tròn $(O)$ và $M,N$ là hai điểm thuộc $(O)$. $P$ là một điểm bất kỳ trên đường tròn đường kính $MN$. Gọi $m,n$ là hai đường thẳng lần lượt qua $M,N$ theo thứ tự song song với $s_M,s_N$. Khi đó thì đối xứng của $m,n$ lần lượt qua $PM,PN$ cắt nhau trên $(O)$.

 

 

Chứng minh. Bổ đề được chứng minh đơn giản bằng cộng góc. Thật vậy, gọi $m'$ và $n'$ lần lượt là đối xứng của $m,n$ qua $PM,PN$. Ta có biến đổi góc

 

$(m',n')=(m',PM)+(PM,PN)+(PN,n')(\bmod\pi)$

 

$=(PM,m)+(PN,PM)+(n,PN)(\bmod\pi)$ (Do $PM\perp PN$ nên $(PM,PN)=\frac{\pi}{2}=-\frac{\pi}{2}=(PN,PM)(\bmod\pi)$)

 

$=(n,m)(\bmod\pi)$

 

$=\frac{1}{2}(\overrightarrow{OM},\overrightarrow{ON})(\bmod\pi)$.

 

Ta chú ý $m'$ và $n'$ đi qua $M,N$ nên từ đó $m'$ và $n'$ cắt nhau trên $(O)$. Ta có điều phải chứng minh.

 

Giải bài toán.

 

 

Gọi $K',L'$ là ảnh của $K,L$ qua phép vị tự tâm $H$ tỷ số $2$. Vì $S$ cũng là ảnh của $T$ qua phép vị tự tâm $H$ tỷ số $2$ nên ta chỉ cần chứng minh $S$ là trung điểm của $K'L'$ thì bài toán được giải quyết. Thật vậy, theo bổ đề 2 dễ thấy phép vị tự tâm $H$ biết $s_M,s_N$ thành các đường thẳng $K'M,K'N$. Từ đó ta có $(K'M,K'N)=(s_M,s_N)=\frac{1}{2}(\overrightarrow{ON},\overrightarrow{OM})(\bmod\pi)$.

 

Vậy nếu gọi $R_1$ là đối xứng của $K'$ qua $MN$ thì $(R_1M,R_1N)=-(K'M,K'N)=\frac{1}{2}(\overrightarrow{OM},\overrightarrow{ON})(\bmod\pi)$ vậy suy ra $R_1$ thuộc $(O)$.

 

Tương tự nếu $R_2$ đối xứng $L'$ qua $PQ$ thì $R_2$ thuộc $(O)$.

 

Mặt khác từ việc lấy đối xứng ta có $R_1N,R_2P$ lần lượt là đối xứng của $NK',PL'$ theo thứ tự qua $SN,SP$. $S$ lại nằm trên đường tròn đường kính $NP$ vậy theo bổ đề 3 thì hai đường thẳng này phải có chung một điểm thuộc $(O)$. Vậy từ đó $R_1\equiv R_2\equiv R\in (O)$. Từ đó theo tính chất đối xứng trục, hai trục $MN,PQ$ vuông góc do đó $L'=\mathcal{R}_{PQ}(R)=\mathcal{R}_{PQ}[\mathcal{R}_{MN}(K')]=\mathcal{R}_{PQ}\circ \mathcal{R}_{MN}(K')=\mathcal{S}_{S}(K')$ vậy $K'$ và $L'$ đối xứng nhau qua $S$. Từ các nhận xét ban đầu ta thu được điều phải chứng minh.

[quanghung86]

Lời giải sau do bạn Nguyễn Lê Phước gửi tới tác giả.

 

 

Lời giải bài toán 101. Gọi $NI$ cắt $HK$ tại $S$, $MI$ cắt $HL$ tại $T$ thì $S,T$ là tâm bàng tiếp tam giác $ANH,AMH$. Từ đó $\angle ASE=45^\circ=\angle AHL$ và $\angle AES=90^\circ+\angle ANE=\angle ALH$. Từ đó hai tam giác $ASE$ và $ALH$ đồng dạng g.g. Lại có $\angle ATH=90^\circ-\frac{\angle AMN}{2}=180^\circ-\angle AIN=\angle AIS$. Từ đó hai tam giác $ATH$ và $AIS$ đồng dạng g.g. Vậy $\frac{ES}{EI}=\frac{LH}{LT}$. Tương tự $\frac{FT}{FI}=\frac{KH}{KS}$. Từ đó $\frac{FI}{FT}.\frac{LT}{LH}=\frac{EI}{ES}.\frac{KS}{KH}$. Dùng định lý Menelaus dễ thấy $FL,ES$ cùng đi qua một điểm trên $IH$.

 

Lời giải khác của bạn Nguyễn Đức Bảo có thể xem tại http://artofproblems...1308940p7009306, bài toán này nằm trong chuỗi bài mở rộng bài toán IMO 2009 của tác giả http://analgeomatica...-2009-ngay.html

 

Bài toán 102 (Tập huấn đội IMO 2016). Cho tam giác $ABC$ nội tiếp đường tròn $(O)$ cố định. $B$, $C$ cố định, $A$ di chuyển trên $(O)$. $I$ là tâm đường tròn nội tiếp tam giác $ABC$. $K$, $L$ theo thứ tự là trực tâm các tam giác $IAB$, $IAC$. $P$ đối xứng với $O$ qua trung điểm $KL$. Chứng minh rằng $AP$ đi qua một điểm cố định khi $A$ thay đổi.

Bài viết đã được chỉnh sửa nội dung bởi quanghung86: 04-01-2017 - 20:54
Thay đổi đề bài 102.

[moonkey01]

Lời giải sau do bạn Nguyễn Lê Phước gửi tới tác giả.

 

Figure4051.png

 

Lời giải bài toán 101. Gọi $NI$ cắt $HK$ tại $S$, $MI$ cắt $HL$ tại $T$ thì $S,T$ là tâm bàng tiếp tam giác $ANH,AMH$. Từ đó $\angle ASE=45^\circ=\angle AHL$ và $\angle AES=90^\circ+\angle ANE=\angle ALH$. Từ đó hai tam giác $ASE$ và $ALH$ đồng dạng g.g. Lại có $\angle ATH=90^\circ-\frac{\angle AMN}{2}=180^\circ-\angle AIN=\angle AIS$. Từ đó hai tam giác $ATH$ và $AIS$ đồng dạng g.g. Vậy $\frac{ES}{EI}=\frac{LH}{LT}$. Tương tự $\frac{FT}{FI}=\frac{KH}{KS}$. Từ đó $\frac{FI}{FT}.\frac{LT}{LH}=\frac{EI}{ES}.\frac{KS}{KH}$. Dùng định lý Menelaus dễ thấy $FL,ES$ cùng đi qua một điểm trên $IH$.

 

Lời giải khác của bạn Nguyễn Đức Bảo có thể xem tại http://artofproblems...1308940p7009306, bài toán này nằm trong chuỗi bài mở rộng bài toán IMO 2009 của tác giả http://analgeomatica...-2009-ngay.html

 

Bài toán 102 (Tập huấn đội IMO 2016). Cho tam giác $ABC$ nội tiếp đường tròn $(O)$ và $P$ di chuyển trên cung $BC$ không chứa $A$. Đối xứng của $PA$ qua $PB$, $PC$ lần lượt cắt $AB$, $AC$ tại $F$, $E$. Một đường thẳng vuông góc với $PA$ tại một điểm chia $PA$ theo tỉ số cố định cắt tiếp tuyến tại $A$ của $(AEF)$ tại $Q$. Chứng minh rằng $Q$ luôn thuộc đường thẳng cố định khi $P$ thay đổi.

 

Trong quá trình cố gắng chứng minh bài toán, em phát hiện ra một số tính chất khác như sau. Không mất tính tổng quát, ta giả sử rằng $AB<AC$.

 

Tính chất 1: $EF$ đi qua $D$ là chân đường phân giác ngoài từ $A$ của $\Delta ABC$.

 

Thật vậy, do $NE$ là phân giác $\angle ANC$ nên $\frac{EC}{EA}=\frac{NC}{NA}=\frac{AC}{AH}$. Tương tự ta có $\frac{FA}{FB}=\frac{AH}{AB}$ nên nếu gọi $AD$ là phân giác ngoài của $\Delta ABC$ thì theo định lý Menelaus, chứng minh được $D,E,F$ thẳng hàng.

 

Tính chất 2: $NF,ME,AI$ đồng quy.

 

Từ tính chất 1 và lưu ý rẳng $AI$ là phân giác $\angle BAC$, lại có $AB,AC$ là hai đường đẳng giác trong $\Delta AMN$ nên gọi $AI$ cắt $BC$ tại $P$ thì $(DP,BC)=(DP,NM)=-1$. Mặt khác gọi $AI$ cắt $EF$ tại $S$ thì $A(DP,BC)=A(DS,FE)=(DS,FE)=-1=(DP,NM)$ nên $SP,NF,ME$ đồng quy hay $NF,ME$ cắt nhau trên $AI$.

[moonkey01]

 

Bài toán 102 (Tập huấn đội IMO 2016). Cho tam giác $ABC$ nội tiếp đường tròn $(O)$ cố định. $B$, $C$ cố định, $A$ di chuyển trên $(O)$. $I$ là tâm đường tròn nội tiếp tam giác $ABC$. $K$, $L$ theo thứ tự là trực tâm các tam giác $IAB$, $IAC$. $P$ đối xứng với $O$ qua trung điểm $KL$. Chứng minh rằng $AP$ đi qua một điểm cố định khi $A$ thay đổi.

 

Lời giải của em như sau.

 

Trước hết, ta phát biểu hai bổ đề sau:

 

Bổ đề 1: Hai tam giác đồng dạng có hai cặp cạnh tương ứng vuông góc thì cặp cạnh còn lại cũng vuông góc.

 

Bổ đề 2: $KL,AF$ vuông góc trên $(I)$ với $F$ là tiếp điểm đường tròn bàng tiếp góc $\angle BAC$ của tam giác $ABC$.

 

Hai bổ đề trên đều quen thuộc nên không trình bày lại phép chứng minh tại đây, riêng bổ đề 2 chính là hệ quả bài toán 3 trong kỳ thi Olympic Sharygin vòng 1 năm 2017. Quay trở lại bài toán ban đầu. Do trường hợp $AB=AC$ là hiển nhiên nên không mất tính tổng quát, ta xét trường hợp $AB<AC$ và vị trí các điểm như hình vẽ.

 

Do $K,L$ là trực tâm các tam giác $IAB,IAC$ và $I$ là tâm nội tiếp tam giác $ABC$ nên ta có:

$\angle KAL=\angle KAB+\angle LAC-\angle BAC=90^{o}-\frac{\angle ABC}{2}+90^{o}-\frac{\angle BCA}{2}-\angle BAC=90^{0}-\frac{\angle BAC}{2}$

 

Gọi $Q$ là điểm sao cho $AQ\perp BC$ và $QP||AL$ thì ta có:

$\angle KAQ=\angle BAK-\angle BAQ=90^{o}-\frac{\angle ABC}{2}-(90^{o}-\angle ABC)=\frac{\angle ABC}{2}=\angle IBC$.

 

Mặt khác do $\angle AKQ=180^{o}-\angle KAL=180^{o}-(90^{o}-\frac{\angle BAC}{2})=90^{o}+\frac{\angle BAC}{2}=\angle BIC$ nên tam giác $AKQ$ đồng dạng tam giác $BIC$ (g.g). Gọi $M,N$ là trung điểm $AQ,BC$ thì tam giác $AKM$ đồng dạng tam giác $BIN$ (c.g.c). Từ bổ đề dễ dàng có $KM\perp IN$, lại có $KL\perp AF$ nên ta chỉ cần chứng minh rằng $IN||AF$. Nhưng điều này đúng do dễ dàng tính toán theo 3 cạnh tam giác $ABC$ bởi tính chất phân giác để có tỉ lệ $\frac{IE}{IA}=\frac{BC}{CA+AB}=\frac{NE}{NF}$. Từ đó dẫn đến $KM\equiv KL\perp IN$, lại có $\Delta MAL=\Delta MQK$ (g.c.g) nên $ML=MK$ hay $M$ là trung điểm $KL$ hay $M$ cũng là trung điểm $OP$. Lại có $\frac{AQ}{BC}=\frac{AK}{BI}=cot\frac{\angle BAC}{2}$ không đổi nên $AQ$ không đổi. Gọi $R$ là đối xứng của $P$ qua $A$ thì $OR=AQ$ không đổi, lại có $OR||AP\perp BC$ nên $AP$ luôn qua $R$ cố định $\blacksquare$

 

Thầy có lời giải nào mà để tránh tính toán phần sau không ạ ?

 

Hình vẽ bài toán:

Hình gửi kèm

• 

Bài viết đã được chỉnh sửa nội dung bởi moonkey01: 05-01-2017 - 16:52

[moonkey01]

Em giải thích rõ hơn phần tính toán để có được $IN||AF$.

 

Đặt $BC=a,CA=b,AB=c(b\neq c)$ thì dễ dàng có $\frac{IE}{IA}=\frac{a}{b+c}$. Mặt khác cũng tính được $BE=\frac{ca}{c+b}$ nên $NE=BN-BE=\frac{a}{2}-\frac{ca}{c+b}=\frac{a(b-c)}{2(b+c)}$. Hơn nữa $NF=NC-CF=\frac{a}{2}-\frac{c+a-b}{2}=\frac{b-c}{2}$ nên $\frac{NE}{NF}=\frac{a(b-c)}{2(b+c)}:\frac{b-c}{2}=\frac{a}{b+c}=\frac{IE}{IA}$. Theo định lý Thales đảo, $IN||AF$.

 

Bài toán 103 (Mathematical Refections 6/2014). Cho tam giác $ABC$ nội tiếp $(\Gamma)$ có $M$ là điểm chính giữa cung $BC$ không chứa $A$. Gọi $l_{b},l_{c}$ là đường thẳng qua $B,C$ song song $AM$ và cắt lại $(\Gamma)$ tại $P,Q$. $PQ$ cắt $AB,AC$ tại $X,Y$. $AM$ cắt lại $(AXY)$ tại $N$. Chứng minh rằng trung trực $BC,XY,MN$ đồng quy.

[quanghung86]

Cám ơn Hoàng cho lời giải thú vị khác đáp án cho bài toán 102. Sau đây là đáp án của thầy. Phần đầu của chứng minh này có tham khảo trên AoPS nhưng mình không tìm lại link, xin trích dẫn sau.

 

 

Lời giải bài toán 102. Gọi $CI$, $BI$ lần lượt cắt đường tròn $(AIB)$, $(AIC)$ tại $I_c$, $I_b$ thì $I_c$, $I_b$ chính là các tâm đường tròn bàng tiếp góc $C$, góc $B$ của tam giác $ABC$. Do đó $I_c$, $A$, $I_b$ thẳng hàng. Mặt khác do $I_cB\parallel AK$, $BK\parallel AI_c$ nên $I_cAKB$ là hình bình hành từ đó $K$ đối xứng $I_c$ qua trung điểm $AB$. Tương tự thì $L$ đối xứng $I_b$ qua trung điểm $AC$. Gọi $E$, $F$, $H$, $N$ lần lượt là trung điểm $CA$, $AB$, $KL$, $I_cI_b$ thì $H$, $N$ đối xứng nhau qua trung điểm $EF$ nên $AH\perp BC$ hay $AH\parallel ON$. Gọi $M$ là trung điểm $BC$ thì $A$ đối xứng $M$ qua trung điểm $EF$. Do đó $AHMN$ là hình bình hành suy ra $AH=MN$ nên $AH$ có độ dài không đổi. $AP$ cắt $OM$ tại $Q$ thì tính chất đường trung bình cho ta $OQ=2AP$ suy ra $OQ$ không đổi hay $Q$ cố định. Vậy $AP$ đi qua điểm $Q$ cố định khi $A$ thay đổi.

 

 

Và lời giải bài 103.

 

 

Lời giải bài toán 103. Dễ thấy $AM$ là phân giác ngoài góc $\angle BAC$ nên $N$ là trung điểm cung $XY$ chứa $A$ của đường tròn $(K)$ ngoại tiếp tam giác $AXY$ nên trung trực $XY$ đi qua $N$. Dễ thấy trung trực $BC$ đi qua $M$. Gọi trung trực $BC$ và $XY$ cắt nhau tại $R$. Ta sẽ chứng minh tam giác $RMN$ cân thì trung trực $MN$ đi qua $R$, thật vậy. Gọi $AD$ là phân giác của tam giác $ABC$ dễ thấy $AD\perp MN$, ta có biến đổi góc. 

 

$$(RM,MN)=(BC,AD)=(BC,BP)+(BP,AD)=(QC,QP)+(AD,QC)=(PQ,AD)=(MN,RN)$$.

 

Từ đó tam giác $RMN$ cân tại $R$.

 

Bài toán 104 (Tập huấn đội IMO 2016, tập huấn đội KHTN 2017). Cho tam giác $ABC$ nhọn, nội tiếp đường tròn $(O)$. Phân giác $AD$, $BE$, $CF$. $X$, $Y$, $Z$ lần lượt là trung điểm cung $BC$ chứa $A$, cung $CA$ chứa $B$, cung $AB$ chứa $C$. Trung trực $CA$, $AB$ cắt $AZ$, $AY$ tại $A_1$, $A_2$. $U$ đối xứng $A$ qua $A_1A_2$. Tương tự có $U$, $W$. Chứng minh rằng tiếp tuyến qua $A$, $B$, $C$ của các đường tròn $(ADU)$, $(BEV)$, $(CFW)$ đồng quy.

 

 

[quanghung86]

Lời giải bài toán 104. 

 

Bổ đề. Cho tam giác $ABC$, $I_a$ là tâm đường tròn bàng tiếp ứng với $\angle A$. $M$ đối xứng $I_a$ qua $BC$. Khi đó $AM$ song song với đường thẳng $Euler$ của tam giác $I_aBC$.

 

Chứng minh sau của bạn Đỗ Xuân Long lớp 11 toán THPT chuyên KHTN.

 

 

Chứng minh. Gọi $X$ là điểm chính giữa cung $BC$ không chứa $A$, $H$ là trực tâm tam giác $I_aBC$. Ta có $\triangle I_aXB\sim \triangle I_aCM$ nên $I_aM\cdot I_aX=I_aB\cdot I_aC$. Mặt khác do $\frac{1}{2}\angle A+\angle BI_aC=90^\circ$ nên $\triangle I_aHC\sim\triangle I_aBA$ suy ra $I_aH\cdot I_aA=I_aB\cdot I_aC$. Từ đó $I_aX\cdot I_aM=I_aH\cdot I_aA$ nên theo định lý Thales, $AM\parallel XH$.

 

 

Giải bài toán. $I$ là tâm đường tròn nội tiếp tam giác $ABC$. Chú ý rằng đường tròn tâm $A_1$ qua $A$, $C$ trực giao với đường tròn $(AIB)$ và đường tròn tâm $A_2$ qua $A$, $B$ trực giao với $(AIC)$. Xét hợp của phép nghịch đảo cực $A$ phương tích $AB\cdot AC$ với phép đối xứng qua phân giác $\angle A$. Dưới phép biến hình này, $U$ biến thành trực tâm tam giác $JBC$. $D$ biến thành giao điểm của $AD$ với đường tròn $(ABC)$. Từ đó đường tròn $(ADU)$ biến thành đường thẳng Euler của tam giác $JBC$. Theo bổ đề trên thì nếu gọi $K$ là đối xứng của $J$ qua $BC$ thì $AK$ song song với đường thẳng Euler của tam giác $JBC$. Do đó theo nghịch đảo thì tiếp tuyến tại $A$ của $(ADU)$ đi qua ảnh nghịch đảo của $I$ qua đường tròn $(ABC)$. Tương tự ta suy ra các tiếp tuyến qua $A$, $B$, $C$ của các đường tròn $(ADU)$, $(BEV)$, $(CFW)$ đồng quy.

 

Chú ý. Phép nghịch đảo bảo toàn sự đối xứng. Người ta còn gọi phép nghịch đảo qua một đường tròn là phép đối xứng qua đường tròn. Sự bảo toàn tính đối xứng có thể phát biểu như sau: trong mặt phẳng, cho trước hai điểm $A$ và $B$ đối xứng nhau qua một đường tròn $\mathcal{C}$(có thể suy biến thành đường thẳng), ảnh của $A$ và $B$ dưới một phép nghịch đảo sẽ đối xứng qua ảnh của $\mathcal{C}$ cũng dưới phép nghịch đảo đó.

 

Xin cám ơn bạn Ngô Quang Dương sinh viên ĐHKHTN đã giúp tôi biên tập lời giải này.

 

Bài toán 105.(Mở rộng ý a) VMO 2017 bài toán 3). Cho tam giác $ABC$ nội tiếp đường tròn $(O)$. Một đường tròn $(K)$ đi qua $B,C$ cắt $CA,AB$ tại $E,F$ khác $B,C$. $BE$ cắt $CF$ tại $H$. $AH$ cắt $(O)$ tại $D$ khác $A$. Tiếp tuyến tại $E,F$ của $(K)$ lần lượt cắt $DB,DC$ tại $M,N$. Chứng minh rằng $MN\perp OH$.

[moonkey01]

Bài toán 105.(Mở rộng ý a) VMO 2017 bài toán 3). Cho tam giác $ABC$ nội tiếp đường tròn $(O)$. Một đường tròn $(K)$ đi qua $B,C$ cắt $CA,AB$ tại $E,F$ khác $B,C$. $BE$ cắt $CF$ tại $H$. $AH$ cắt $(O)$ tại $D$ khác $A$. Tiếp tuyến tại $E,F$ của $(K)$ lần lượt cắt $DB,DC$ tại $M,N$. Chứng minh rằng $MN\perp OH$.

 

Bổ đề: Cho tam giác $ABC$ nội tiếp $(O)$. Đường tròn $(K)$ đi qua $B,C$ cắt $CA,AB$ tại $E,F$. $BE$ cắt $CF$ tại $H$. Gọi $AT$ là đường kính của $(O)$. Khi đó $T,K,H$ thẳng hàng.

 

Lời giải bài toán 105: Gọi $L$ là giao điểm của $ME,AH$ thì ta có $\angle LEB=\angle ACB=\angle ADB$ nên $BDEL$ nội tiếp, dẫn đến $HL.HD=HE.HB=HF.HC$ hay $CDFL$ nội tiếp. Từ đó $\angle LFC=\angle ADC=\angle ADC$ nên $FL$ là tiếp tuyến của $(K)$ và $N,F,L$ thẳng hàng. Mặt khác $ML.ME=MB.MD$ và $NL.NF=NC.ND$ nên $MN$ chính là trục đẳng phương của $(LEF)$ và $(K)$, nên ta chỉ cần chứng minh tâm của $(LEF)$ nằm trên $OH$ hay $OH$ chia đôi $LK$. Gọi $AT$ là đường kính của $(O)$, do $BCEF$ nội tiếp nên dễ dàng chứng minh được $EF\perp AT$, mà $EF||LK$ (tính chất tiếp tuyến) nên $LK||EF$. Theo bổ đề, $T,K,H$ thẳng hàng mà $OH$ chia đôi $AT$ nên $OH$ chia đôi $LK$. Vậy $MN\perp OH$.

 

Một hệ quả của bài toán là $MN,EF,BC$ đồng quy, Thật vậy, nếu gọi $EF$ cắt $BC$ tại $S$ thì $SE.SF=SB.SC$ nên $S$ nằm trên trục đẳng phương của $(LEF)$ và $(K)$ hay $MN,EF,BC$ đồng quy.

 

Hình vẽ bài toán 105 ở phần dưới.

 

Bài toán 106 (Sưu tầm): Cho tam giác $ABC$ nhọn có $AD,BE,CF$ là đường cao và trực tâm $H$. $I$ là tâm nội tiếp tam giác $AEF$. Gọi $M,N$ là điểm trên $(IAB),(IAC)$ sao cho $BM,CN$ là phân giác $\angle ABC, \angle ACB$. Chứng minh rằng trung tuyển qua $M,N$ của tam giác $MHB,NHC$ cắt nhau trên $(DEF)$.

Hình gửi kèm

• 

Bài viết đã được chỉnh sửa nội dung bởi moonkey01: 08-01-2017 - 22:19

[Ngockhanh99k48]

$\boxed{\text{Lời giải bài toán 106}}$
Gọi $M$ là tâm nội tiếp $\triangle BDF$. Ta sẽ chứng minh $M \in (IAB)$. Ta có $\triangle FBD \cap M \stackrel{+}{\sim} \triangle FEA \cap I$, do đó $\widehat{AIM}=\widehat{AIF}+\widehat{FIM} = 90^{\circ}+\frac{\widehat{AEF}}{2}+\widehat{FAD}=180^{\circ}-\frac{\widehat{ABC}}{2} = 180^{\circ} - \widehat{ABM}$ nên $A, I, M, B$ đồng viên. Tương tự ta sẽ suy ra $N$ là tâm nội tiếp $\triangle CDE$.
Gọi $K, L$ là trung điểm $HB, HC$. Kẻ đường kính $EP$ của $(CDE)$. Rõ ràng $EP$ đi qua $L$. Ta có $\triangle DBF \cap KMH \stackrel{+}{\sim} \triangle DEC \cap LNP$. Gọi $Q, O$ là tâm ngoại tiếp $\triangle DEF, \triangle ABC$ thì $Q$ là trung điểm $OH$. Ta có $\frac{1}{2} (QK, QL) \equiv \frac{1}{2} (OB, OC) \equiv (AB, AC)$ $\equiv$ $(HC, HE) \equiv (EH, EL) \equiv (EH, KM)+(KM, LN)+(LN, EL) \equiv (KM, LN)$ (mod $\pi$). Biểu thức cuối đúng do $\triangle BKM \stackrel {+}{\sim} \triangle ELN$. Từ đó ta suy ra $KM$ cắt $LN$ thuộc $(Q)$.
$\boxed{\text{Bài toán 107}}$ (Nguyễn Minh Hà) Cho tam giác ABC không cân tại $A$, $BB', CC'$ là các đường cao. $M, N$ thứ tự là trung điểm $AC, AB$. $E, F$ thứ tự là tâm nội tiếp $(I)$ và $AC, AB$. $P, Q$ theo thứ tự là giao điểm của $BB', CC'$ và $MI, NI$. $L$ là giao điểm của $EF$ và $PQ$. Chứng minh $IL \parallel BC$.

Bài viết đã được chỉnh sửa nội dung bởi Ngockhanh99k48: 09-01-2017 - 21:40

[quanghung86]

Cám ơn Khánh đã giải và gửi bài mới, bài toán của thầy Hà quả thật rất thú vị. Mình xin đưa ra lời giải của mình như sau.

 

Ta chú ý rằng có một tính chất quen thuộc từ cấu hình trên là $BP=CQ=r$ là bán kính nội tiếp tam giác $ABC$. Do đó để đẹp hơn ta nên phát biểu như sau

 

Bài toán 107'. Cho tam giác $ABC$ có đường tròn nội tiếp $(I)$ tiếp xúc với $CA,AB$ tại $E,F$. $P,Q$ đối xứng với $I$ lần lượt qua trung điểm $BE,CF$. $PQ$ cắt $EF$ tại $R$. Chứng minh rằng $IR\parallel BC$.

 

 

Lời giải. Gọi $IB,IC$ cắt $EF$ tại $M,N$ dễ thấy $M,N$ nằm trên đường tròn đường kính $BC$. Gọi $BK,CL$ là đường cao của tam giác $ABC$. Ta thấy $FQ\parallel CN$ nên $\angle QFM=\angle CNM=\angle CBM=\angle CLM$. Từ đó tứ giác $FMQL$ nội tiếp nên $QM\perp MN$. Tương tự $PN\perp MN$. Từ biến đổi góc trên dễ thấy hai tam giác vuông $MFQ$ và $MBC$ đồng dạng suy ra hai tam giác $MFB$ và $MQC$ đồng dạng. Tương tự hai tam giác $NEC$ và $NPB$ đồng dạng. Ta thu được $\frac{RN}{RM}=\frac{NP}{MQ}=\frac{NP}{BP}.\frac{CQ}{MQ}=\frac{NE}{EC}.\frac{BF}{FM}=\frac{IN}{IM}.\frac{IN}{IM}$, ta chú ý đẳng thức cuối có do các tứ giác $INFB$ và $IEMC$ nội tiếp. Vậy $\frac{RN}{RM}=\frac{IN^2}{IM^2}$ nên $IR$ tiếp xúc $(IMN)$ do đó $\angle RIN=\angle IMN=\angle ICB$. Từ đó $IR\parallel BC$.

 

Bài toán 108 (Mở rộng ý a) bài toán 7 VMO 2017). Cho tam giác $ABC$ nội tiếp đường tròn $(O)$. Một đường tròn $(K)$ đi qua $B,C$. Trung trực $BC$ cắt $(K)$ tại $M,N$. $P$ là điểm thuộc $(K)$. $PM$ cắt $CA,AB$ tại $E,F$. $BE$ cắt $CF$ tại $L$. Chứng minh rằng $AL,PN$ và $BC$ đồng quy.