Chủ đề này có 10 trả lời

[Zaraki]

Như vậy bài Tuần 3 tháng 6 đã được thầy Hùng cho lời giải tại đây kèm theo đó là bài toán mới. Xin trích dẫn lại bài toán mới:

 

Cho tam giác $ABC$ nội tiếp đường tròn $(O)$ cố định vớ $B,C$ cố định và $A$ di chuyển trên $(O)$. Gọi $P,Q$ là hai điểm Isodynamic của tam giác $ABC$. $K$ đối xứng $A$ qua $BC$. $OK$ cắt đường tròn ngoại tiếp tam giác $KPQ$ tại $R$ khác $K$. Chứng minh rằng đường thẳng $AR$ luôn đi qua điểm cố định khi $A$ thay đổi.

 

[QuangDuong12011998]

Lời giải của mình.

Hai điểm isodynamic là giao điểm của 3 đường tròn Apollonius của $\triangle ABC$ dựng trên $BC$, $CA$, $AB$, lần lượt với tỉ số $\dfrac{AB}{AC}$, $\dfrac{BC}{BA}$, $\dfrac{CA}{CB}$

Hiển nhiên là $\dfrac{KB}{KC}=\dfrac{AB}{AC}$ nên $A$, $K$, $P$, $Q$ thuộc đường tròn Apollonius trên $BC$, tỉ số $\dfrac{AB}{AC}$.

Đường tròn Apollonius thì trực giao với đường tròn ngoại tiếp, do vậy $R$ cũng là nghịch đảo của $K$ qua $(O)$.

Gọi $T$ là giao điểm hai tiếp tuyến tại $B$, $C$ của $(O)$. $M$ là trung điểm $BC$, $I$ là trung điểm $OT$ và $J$ là đối xứng của $O$ qua $M$.

Xét phép nghịch đảo đường tròn $(O)$, kí hiệu $I^{R^2}_O$

\[I^{R^2}_O:A, R\mapsto A, K\Rightarrow I^{R^2}_O: AR\rightarrow (OAK)\]

$A$ và $K$ đối xứng qua $BC$, $O$ và $J$ đối xứng qua $BC$ nên $(OAK)$ luôn đi qua $J$ cố định.

Mà $AR$ là ảnh của $(OAK)$ qua phép nghịch đảo $(O)$ nên $AR$ đi qua nghịch đảo của $J$ qua $(O)$, tức là $AR$ đi qua $I$.

$BC$, $(O)$ cố định nên $T$ cố định, kéo theo  $I$ cố định.

Vậy $AR$ luôn đi qua tâm của $(OBC)$.

 

Hình gửi kèm

• 

[baopbc]

Như vậy bài Tuần 3 tháng 6 đã được thầy Hùng cho lời giải tại đây kèm theo đó là bài toán mới. Xin trích dẫn lại bài toán mới:

 

Cho tam giác $ABC$ nội tiếp đường tròn $(O)$ cố định với $B,C$ cố định và $A$ di chuyển trên $(O)$. Gọi $P,Q$ là hai điểm Isodynamic của tam giác $ABC$. $K$ đối xứng $A$ qua $BC$. $OK$ cắt đường tròn ngoại tiếp tam giác $KPQ$ tại $R$ khác $K$. Chứng minh rằng đường thẳng $AR$ luôn đi qua điểm cố định khi $A$ thay đổi.

Lời giải của em không dùng nghịch đảo và có lẽ cũng đơn giản hơn!

Lời giải. Hai điểm isodynamic là giao điểm của 3 đường tròn Apollonius của tam giác $ABC$ dựng trên $BC,CA,AB$ lần lượt với tỉ số $\frac{AB}{AC},\frac{BC}{BC},\frac{CA}{CB}$. Do tâm đường tròn ngoại tiếp tam giác $APQ$ nằm trên $BC$ nên $K$ thuộc $(APQ)$.

Giả sử $(O_a)$ là đường tròn Apollonius ứng với $BC$ theo tỉ số $\frac{AB}{AC}$

$N\equiv (O)\cap (APQ)$. Do đường tròn Apollonius trực giao với $(O)$ nên $OA,ON$ lần lượt là các tiếp tuyến tại $A,N$ của $(O_a)$

$\implies ARNK$ là tứ giác điều hòa $\implies A(ORNK)=-1$

$T\equiv AN\cap $ đường thẳng qua $O$ vuông góc với $BC\implies AR$ chia đôi $OT$. Mặt khác do $ABRC$ là tứ giác điều hòa nên tiếp tuyến tại $B,C$ và $AN$ đồng quy $\implies T$ cố định hay $AR$ đi qua một điểm cố định khi $A$ thay đổi.$\blacksquare$

Bài viết đã được chỉnh sửa nội dung bởi baopbc: 20-06-2016 - 12:53

[quanghung86]

Cám ơn Dương và Bảo, cách giải của các em khác cách của thầy nhiều, với cách nhìn của các em đúng là rất thú vị , hãy đón đọc lời giải tuần sau.

[quanghung86]

Bài toán tổng quát. Cho tam giác $ABC$ và $P$ nằm trong tam giác sao cho $\angle PBA=\angle PCA$. $Q$ là đẳng giác của $P$. $K$ là tâm đường tròn $(QBC)$. $AP$ cắt đường tròn $A$-Apollonius tại $R$ khác $A$. Chứng minh rằng $QR$ và $AK$ cắt nhau trên đường tròn $A$-Apollonius.

 

[Ngockhanh99k48]

Bài toán tổng quát. Cho tam giác $ABC$ và $P$ nằm trong tam giác sao cho $\angle PBA=\angle PCA$. $Q$ là đẳng giác của $P$. $K$ là tâm đường tròn $(QBC)$. $AP$ cắt đường tròn $A$-Apollonius tại $R$ khác $A$. Chứng minh rằng $QR$ và $AK$ cắt nhau trên đường tròn $A$-Apollonius.

 

Figure3881.png

$AK$ cắt $A$-Apollonius tại $L$ khác $A$. Ta sẽ chứng minh rằng $AP, QL$ cắt nhau tại $A$-Apollonius.

$P, Q$ liên hợp đẳng giác trong $\triangle ABC$, kết hợp $\widehat{PBA}=\widehat{PCA}$ ta có $Q$ thuộc trung trực $BC$. Do đó $K$ cũng thuộc trung trực $BC$. 

Gọi đường tròn $A$-Apollonius là đường tròn $(T)$. $AD$ là đường phân giác trong góc $\widehat{BAC}$ của $\triangle ABC$. Hiển nhiên $D \in (T)$.

$AP, AQ$ cắt $(T)$ tại $R, S$. $A, R, S, D$ đồng viên và $AD$ là phân giác $\widehat{RAS}$ nên $DR=DS$. Do đó $R, S$ đối xứng nhau qua $TD \equiv BC$. Cuối cùng ta sẽ chứng minh $QL$ đi qua $R$.

Gọi $M$ là trung điểm $BC$. Ta có: 

$KT^2-KB^2=MT^2-MB^2=(\overline{MT} - \overline{MB})(\overline{MT}+\overline{MB})=(\overline{MT}-\overline{MB})(\overline{MT}-\overline{MC})=\overline{BT}.\overline{CT}=TA^2$.

hay $KQ^2=KT^2-TA^2=P_{K/(T)}=\overline{KL}.\overline{KA}$. Do đó $\widehat{KQL}=\widehat{KAQ}=\widehat{MRL}$. Do $MR \parallel QK$ nên $QL$ đi qua $R$. Ta có đpcm. 

Bài viết đã được chỉnh sửa nội dung bởi Ngockhanh99k48: 20-06-2016 - 21:24

[quanghung86]

Cách khác tổng quát bài này, ta có thể thay hai điểm Isodynamic bằng hai điểm bất kỳ nghịch đảo qua $(O)$.

 

Cho tam giác $ABC$ nội tiếp đường tròn $(O)$ cố định vớ $B,C$ cố định và $A$ di chuyển trên $(O)$. Gọi $P,Q$ là hai điểm bất kỳ nghịch đảo nhau qua $(O)$. $K$ đối xứng $A$ qua $BC$. $OK$ cắt đường tròn ngoại tiếp tam giác $KPQ$ tại $R$ khác $K$. Chứng minh rằng đường thẳng $AR$ luôn đi qua điểm cố định khi $A,P,Q$ thay đổi.

 

Có thể thay $K$ thành 1 điểm cố định nhưng khi đó đường $AR$ có tính chất gì đặc biệt mình cũng chưa nhìn ra ?

[QuangDuong12011998]

Với cách tổng quát thứ hai thì em vẫn nghịch đảo như bài cũ.

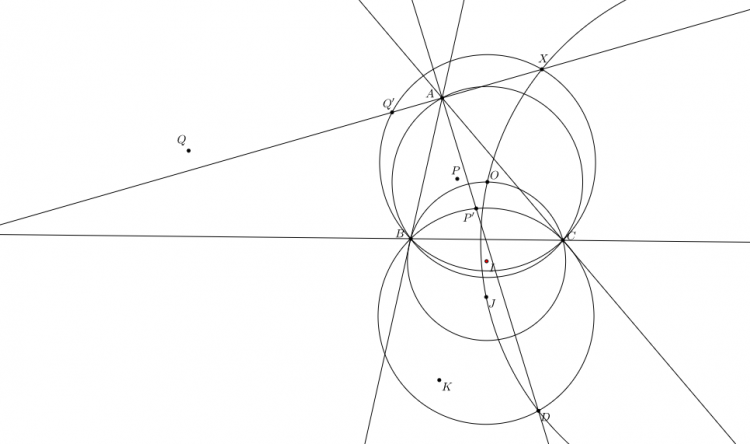
Bổ đề. $P$, $Q$ đẳng giác. $PA$ cắt $(PBC)$ tại $D$. $\Psi_A$ là hợp của phép nghịch đảo cực $A$, phương tích $AB\cdot AC$ với phép đối xứng qua phân giác góc $A$. Thì $\Psi_A(Q)=D$.

$P'$, $Q'$ đẳng giác với $P$, $Q$. Mà $P$, $Q$ là nghịch đảo của nhau qua $(O)$ nên $P'$, $Q'$ là hai điểm đối giác(antigonal image)

Hai điểm đối giác có tính chất $(P'B,P'C)+(Q'B,Q'C)=(P'C,P'A)+(Q'C,Q'A)=(P'A,P'B)+(Q'A,Q'B)=0\pmod\pi$

Cho $P'A$, $Q'A$ cắt $(P'BC)$, $(Q'BC)$ tại $D$, $X$.

Đã có $(DB,DC)=-(XB,XC)$. Lại có $(BC,BD)=(P'C,P'D)=(P'C,P'A)=-(Q'C,Q'A)=-(Q'C,Q'X)=-(BC,BX)$

Từ đó mà $X$, $D$ đối xứng qua $BC$.

$I$ là tâm $(OBC)$. $J$ đối xứng với $O$ qua $BC$.

$I$, $J$ là nghịch đảo của nhau qua $(O)$. Lấy $A_1$, $A_2$ là giao của $(O)$ với trung trực $BC$ thì $\overline{OA_1}^2=\overline{OA_2}^2=\overline{OI}\cdot\overline{OJ}$ nên $(A_1,A_2,I,J)$ là hàng điều hòa, vậy $AI$, $AJ$ đẳng giác.

Theo bổ đề thì

\[\Psi_A: AI,OK,(KPQ)\rightarrow AJ,(AOK),(ODX)\]

Do đối xứng qua $BC$ mà có ngay $(AOK)$, $(ODX)$ đi qua $J$.

Vậy kết luận $AI$, $OK$, $(KPQ)$ đồng quy, tức là $AR$ luôn đi qua tâm $(OBC)$ cố định.

_____________________________________

Tổng quát sau cùng của thầy em thấy không ổn? $K$, $R$ là nghịch đảo của nhau qua $(O)$ thì $R$ cố định.

Hình gửi kèm

• 

[Ngockhanh99k48]

Một lời giải khác cho bài toán tổng quát thứ hai:
$P$ và $Q$ là ảnh nghịch đảo của nhau qua đường tròn $(O)$. Do đó $OA^2=OP.OQ=OK.OR$. Gọi $(J)$ là tâm $(OBC)$ và $O'$ là đối xứng của $O$ qua $BC$. Gọi $M$ là trung điểm $BC$ và $OM$ cắt $(OBC)$ tại $N$. Ta cũng có $OB^2=OM.ON=OJ.OO'$. Do đó $OK.OR=OJ.OO'$ hay $K, R, O', J$ đồng viên. Kết hợp $\triangle OAR \stackrel{+}{\sim} \triangle OKA$, ta có $(RA, RO) \equiv (AO, AK) \equiv (OA, OO') \equiv (OO', O'K)$ (do $O, O'$ và $A, K$ đối xứng nhau qua $BC$) $\equiv (O'J, O'K) \equiv (RJ, RK)$ (mod $\pi$). Do $O, R, K$ thẳng hàng nên $A, R, J$ thẳng hàng hay $AR$ đi qua tâm $(OBC)$ cố định.

[quanghung86]

Tổng quát cuối nên viết thế này Dương ạ.

 

Cho $P,Q$ là nghịch đảo qua $(O)$ và $K$ cố định. Thì $OK$ luôn cắt $(KPQ)$ tại một điểm cố định khi $P,Q$ thay đổi.

[quanghung86]

Cám ơn các em đã đóng góp ý tưởng, tổng quát hơn nữa cho tổng quát thứ hai

 

Cho tam giác $ABC$ nội tiếp đường tròn $(O)$ và $P,Q$ là hai điểm đẳng giác. $AQ$ cắt $(QBC)$ tại $R$ khác $Q$. Đường tròn $(K)$ qua $A,R$ trực giao với $(O)$. $S$ đối xứng $P$ qua trung trực $BC$. $L$ là tâm của $(PBC)$. Chứng minh rằng $RS$ và $AL$ cắt nhau trên $(K)$.

Hình gửi kèm

• 

Bài viết đã được chỉnh sửa nội dung bởi baopbc: 21-06-2016 - 19:34
$Q\rightarrow R$