Chủ đề này có 6 trả lời

[baopbc]

Như vậy thầy Hùng đã đưa ra lời giải bài cũ trong tuần 1 tháng 7 và kèm theo đó là bài toán mới, xin trích dẫn lại bài toán đó.

 

Cho tam giác $ABC$ nội tiếp trong đường tròn $(O)$ với đường cao $AH.E,F$ lần lượt thuộc $CA,AB$ sao cho $EF\parallel BC$. Trên tiếp tuyến tại $A$ của $(O)$ lấy $S,T$ sao cho $SF\perp AB,TE\perp AC$. Đường thẳng qua $E$ song song với $AB$ cắt $(O)$ tại $M,N$. Đường thẳng qua $F$ song song với $AC$ cắt $(O)$ tại $P,Q$. Chứng minh rằng giao điểm của $EF,AH$ nằm trên trục đẳng phương của hai đường tròn $(SMN)$ và $(TPQ)$.

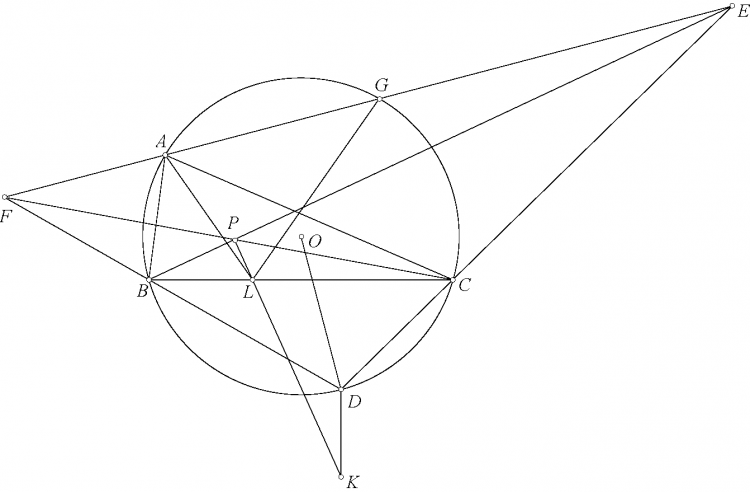
Hình vẽ bài toán

[baopbc]

Trúng tủ rồi!

Lời giải. Do tứ giác $MPNQ$ nội tiếp nên trục đẳng phương của $(SMN)$ và $(TPQ)$ đi qua giao điểm của $MN,PQ$

$X\equiv SE\cap (SMN),Y\equiv TF\cap (TPQ)$. Dễ thấy $EFST$ là tứ giác nội tiếp nên $\angle YFB=\angle XEC$

Mặt khác $EY.ET=EP.EQ=EA.EB$ nên $BYAT$ là tứ giác nội tiếp. Tương tự thì $CXAS$ là tứ giác nội tiếp.

Do đó $\angle FYB=\angle BAT,\angle EXC=\angle EAS$. Mặt khác $\frac{\sin \angle BAT}{\sin \angle CAS}=\frac{AC}{AB}=\frac{EC}{FB}$ nên $YB=XC$

$\implies XY\parallel BC\parallel EF\implies STXY$ là tứ giác nội tiếp $\implies $trục đẳng phương của $(SMN)$ và $(TPQ)$ đi qua giao điểm của $XS$ và $YT$

Theo kết quả USA TSTST 2016 (# 10) ta suy ra trục đẳng phương của $(SMN)$ và $(TPQ)$ đi qua giao điểm của $AH$ với $EF.\blacksquare$

[quanghung86]

Chuẩn rồi Bảo, bài này thầy mở rộng USA TST 2016, chính xác là dựa vào ý tưởng của em giải được, xung quanh bài toán gốc này và mở rộng có nhiều thú vị lắm, mọi người hãy cùng thảo luận !

[quanghung86]

Mình xin đề xuất một phát triển khác như sau

Cho hình chữ nhật $ABCD$ và điểm $P$ nằm trên cạnh $AB$. Đường tròn $(K)$ qua $P,D$ tiếp xúc $PC$ và đường tròn $(L)$ qua $P,C$ tiếp xúc $PD$. Một đường thẳng song song với $CD$ cắt $(K),(L)$ lần lượt tại $Q,R,M,N$. Gọi $U,V$ là tâm các đường tròn $(BQR),(AMN)$. $UV$ cắt $KL$ tại $G$. Gọi $O$ là tâm ngoại tiếp tam giác $PCD$. Chứng minh rằng $\angle POG=90^\circ$.

[quanghung86]

Một mở rộng khác cho USA TST

 

Cho tam giác $ABC$ nội tiếp trong đường tròn $(O)$. $P$ nằm trên trung trực $BC$. $E,F$ thuộc $CA,AB$ sao cho $PE\parallel AB,PF\parallel AC$. $S,T$ là nghịch đảo của $F,E$ qua $(O)$. $PE$ cắt $(O)$ tại $M,N$. $PF$ cắt $(O)$ tại $Q,R$. $CS$ cắt $BT$ tại $D$. Chứng minh rằng $PD$ là trục đẳng phương của $(SMN)$ và $(TQR)$.

 

Bài viết đã được chỉnh sửa nội dung bởi quanghung86: 06-07-2016 - 10:06

[quanghung86]

Một mở rộng thú vị cho bổ đề của Bảo

 

Cho tam giác $ABC$ nội tiếp đường tròn $(O)$. $D$ nằm trên cung $BC$ không chứa $A$. Đường thẳng qua $A$ vuông góc $OD$ cắt $DC,DB$ và $(O)$ tại $E,F,G$. $BE$ cắt $CF$ tại $P$. $K$ là trực tâm tam giác $DBC$. $PK$ cắt $BC$ tại $L$. Chứng minh rằng $\angle ALB=\angle GLC$.

 

Cách cm dùng phương tích và một chút hàng điều hòa !

Hình gửi kèm

• 

[quanghung86]

Bài toán trên phát biểu thành ngũ giác nội tiếp cũng rất thú vị!