Nguồn: fb của bạn Hiếu Digb
Đánh lại vì ảnh nhỏ.
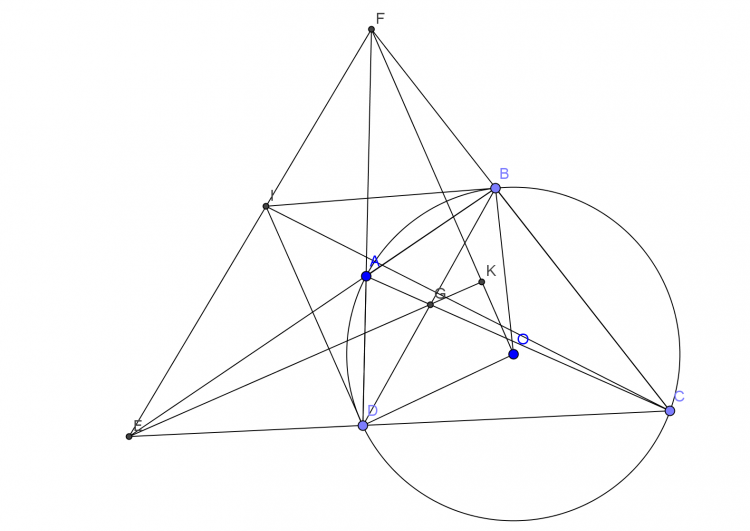
Bài 5. Cho tứ giác lồi $ABCD$ nội tiếp đường tròn tâm $O$, giả sử $O$ không trùng giao điểm $G$ của $AC$ và $BD$ và $O$ không nằm trên đường thẳng $BD$.
Giả sử $AB$ cắt $CD$ tại $E$, $AD$ cắt $BC$ tại $F$. Đường thẳng $OG$ cắt $EF$ tại $I$.
a. chứng minh $BEIC$ $DFIC$ VÀ $OBID$ nội tiếp đường tròn
b. gọi $M$ $N$ là tâm của đường tròn $(BCE)$ và $(DCF)$. Gọi $P$ $Q$ là giao điểm của $(CMN)$ và $(OBD)$. Chứng minh $OI$ $PQ$ và $MN$ đồng quy và tam giác $EAF$ và $MON$ đồng dạng
Bài 6. cho đa thức $P(x)=x^n-(p-1)x+p$ trong đó $n\geq 2$ và $p$ là số nguyên tố. Chứng minh rằng nếu $P(x)$ phân tích thành 2 đa thức với hệ số nguyên khác đa thức hằng số thì $P(x)$ có nghiệm $z$ sao cho $\left | z \right |=1$
Bài 7 Cho $p>5$ là số nguyên tố và $p\neq 107$ ta viết
$\frac{1}{1^{2003}}+\frac{1}{2^{2003}}+...+\frac{1}{(P-1)^{2003}}=\frac{a}{b}$
Trong đó $a$ $b$ là các số nguyên dương nguyên tố cùng nhau. Chứng minh $p^2\setminus a$
@Zaraki: Cho phép mình gộp hai bài viết lại để mọi người dễ đọc + thấy được đề trên trang chủ.
Bài viết đã được chỉnh sửa nội dung bởi Zaraki: 13-08-2016 - 19:42