Chủ đề này có 4 trả lời

[IHateMath]

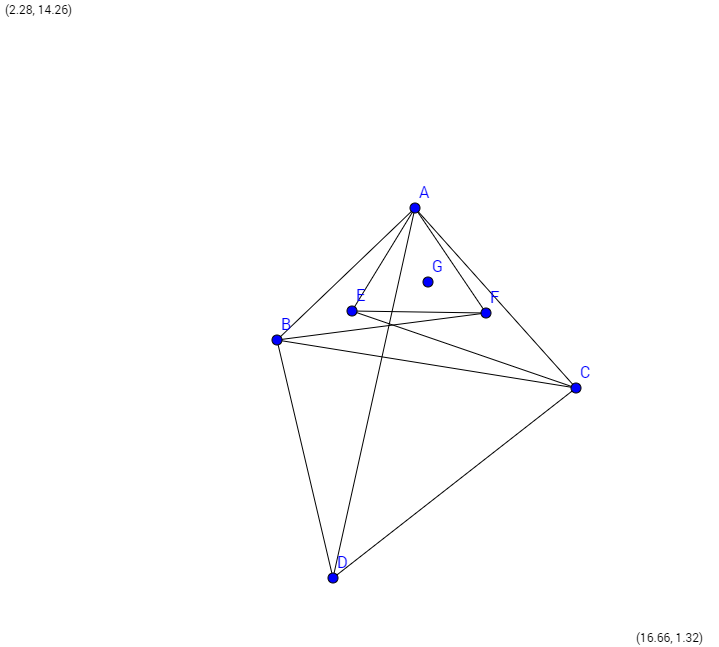
Số $n$ nguyên (ít nhất là $4$) là số đẹp nếu: với bất kỳ bộ $X$ gồm $n$ điểm đồng phẳng và không có $3$ điểm nào thẳng hàng, ta xét một điểm bất kỳ $P$ thuộc $X$ và thấy rằng có một số chẵn tam giác có $3$ đỉnh cũng thuộc $X$ và chứa $P$ ở miền trong thật sự của nó (không trùng với đỉnh). 

i) Chỉ ra một lớp số đẹp.

ii) (câu hỏi mở) Tìm tất cả các số đẹp.

Bài viết đã được chỉnh sửa nội dung bởi IHateMath: 31-08-2016 - 22:16

[JUV]

Số đẹp duy nhất là $5$ thôi, còn dễ thấy $n=4$ hay $6$ đều không thoả mãn, $n=7$ ta có cách sắp xếp sau không thoả mãn

Trong đó $G$ nằm trong các tam giác $ABC$,$ACD$,$AEF$,$AEC$,$AFB$

Với $n>7$, ta sẽ thêm một số điểm nằm khác phía với $C$ bờ $BD$, dịch chuyển những điểm đó ra đủ xa khỏi $7$ điểm $A,B,C,D,E,F,G$ sao cho với mỗi $2$ điểm $X,Y$ trong số các điểm thêm vào, $G$ không thuộc các tam giác $AXY$,$BXY$,$CXY$,$DXY$,$EXY$,$FXY$ nhưng lại thuộc các tam giác $AXF,AXC,AYF,AYC$ và không thuộc tam giác $MNX,MNY$ với $M$,$N$ là $2$ trong số $7$ điểm $A,B,C,D,E,F,G$ trừ $4$ tam giác kể trên. Tất nhiên với mọi $3$ điểm $X,Y,Z$ được thêm thì $G$ không thuộc $XYZ$:

Lúc này luôn có đúng số lẻ tam giác chứa $G$, và chú ý rằng có thể thêm vô hạn điểm nên mọi $n>7$ đều không phải số đẹp. Vậy số đẹp duy nhất là $5$

Bài viết đã được chỉnh sửa nội dung bởi JUV: 01-09-2016 - 10:24

[IHateMath]

Số đẹp duy nhất là $5$ thôi, còn dễ thấy $n=4$ hay $6$ đều không thoả mãn, $n=7$ ta có cách sắp xếp sau không thoả mãn [...] Lúc này luôn có đúng số lẻ tam giác chứa $G$, và chú ý rằng có thể thêm vô hạn điểm nên mọi $n>7$ đều không phải số đẹp. Vậy số đẹp duy nhất là $5$

Bạn ơi $n=7$ được mà! Trong ví dụ trên của bạn thì có $6$ tam giác chứa $G$ lận, bạn chưa thấy thêm $\Delta AFD$ rồi. Còn về việc chỉ ra một lớp số đẹp, có thể chỉ ra các số lẻ $\geq 5$ đều đẹp! Bài này mình mở rộng ra từ bài toán gốc là hãy cm $n=2005$ là số đẹp (đề bài được viết lại cho phù hợp). Đây là câu hỏi trong đề British MO 2005.

[redfox]

Với $n$ chẵn. Lấy đa giác lồi $A_1A_2...A_{n-1}$. $A_1A_3$ cắt $A_2A_4$ tại $O$. Lấy $A_n$ nằm trong tam giác $OA_2A_3$. Khi đó $A_n$ nằm trong đúng $n-3$ tam giác $A_2A_3A_k$ là số lẻ. Vậy nếu $n$ đẹp thì $n$ lẻ.

Ta có điểm $D$ nằm trong tam giác $ABC$ khi và chỉ khi $C$ nằm trong góc đối đỉnh của $\widehat{ADB}$.

Xét $n=2k+1$ lẻ và điểm $P$ bất kì trong $X$. Kẻ các tia $PA_i$ với $i=1;2;...;2k$ và các tia đối của $PA_i$.

Ta chứng minh được tồn tại $2$ tia $PA_i$ và $PA_j$ sao cho không có tia nào ở giữa. Khi đó không có tam giác nào có một cạnh là $A_iA_j$ chứa điếm $P$ và tam giác $A_mA_nA_i$ chứa điểm $P$ khi và chỉ khi tam giác $A_mA_nA_j$ chứa điểm $P$.

Ta dễ chứng minh bằng quy nạp với $k$, số $n$ là đẹp bằng cách loại hai điểm $A_i, A_j$ như trên, khi đó số tam giác chứa điểm $P$ giảm đi một số chẵn. Vậy các số đẹp là các số lẻ $\geq 5$.

Bài viết đã được chỉnh sửa nội dung bởi redfox: 01-09-2016 - 18:46

[JUV]

Xin lỗi vì sự sai sót, bây giờ mình sẽ chứng minh rằng $n$ là số đẹp khi và chỉ khi $n$ lẻ và $n\geq 5$. Xét $n$ lẻ và $n$ điểm trên mặt phẳng. Xét điểm $A$ trong $n$ điểm đó và $n-1$ điểm còn lại là $A_1;A_2;...A_{n-1}$ lần lượt theo chiều kim đồng hồ với trục là $A$. Nối $A$ với $n-1$ điểm còn lại, gọi $S$ là số tam giác chứa $A$. Với $i,j$ bất kì, xét $(i;j)=1$ nếu đoạn thẳng $AA_i$ tạo với đoạn thẳng $AA_j$ một góc bé hơn $180^\circ$ theo chiều kim đồng hồ,$(i;j)=-1$ nếu ngược lại. Ta thấy $A$ nằm trong tam giác $A_iA_jA_t$ khi và chỉ khi $(i;j)=(j;t)=(t;i)$.Với $A_i$ bất kì, gọi $n_i$ là số số $j$ sao cho $(i;j)=1$, $m_i$ là số $j$ sao cho $(i;j)=-1$. Dễ thấy $n_i+m_i=n-1$. Xét $2$ số $A_i$ và $A_j$ bất kì, giả sử $(i;j)=-1$, số các tam giác chứa $A$ có đỉnh là $A_i;A_j$ là số các số $t$ sao cho $(i;j)=(j;t)=(t;i)=-1(1)$. Gọi số đỉnh nằm giữa $A_i$ và $A_j$ theo chiều kim đồng hồ là $s$, dễ thấy $s\equiv i-j \pmod{2}$. Số số $t$ thoả mãn (1) chính là $n_i+m_j-s\equiv i-j+n_i+n_j \pmod {2}$. Cho $i;j$ chạy, lưu ý rằng mỗi tam giác được tính $3$ lần nên ta có $3S \equiv \sum_{i=1}^{n-1}\sum_{j=1}^{i-1} (n_i+n_j+i-j)\equiv 0 \pmod{2}$ nên $S\equiv 0\pmod{2}$. Vậy số tam giác chứa $A$ là số chẵn $\forall A\in X$ nên $n$ là số đẹp. Với $n$ là số chẵn, xét $4$ điểm $A,B,C,D$ sao cho $D$ nằm trong $ABC$. Thêm $1$ số chẵn điểm $T$ vào $X$ sao cho $T$ không cùng phía với $A,D$ bờ $BC$ và với mọi $Y,Z$ được thêm, $D$ không nằm trong $AYZ,BYZ,CYZ$ và không ở trong $ABT,BCT$ với mọi $T$ được thêm nhưng thuộc $ACT$. Vậy luôn có lẻ số tam giác chứa $D$