Chủ đề này có 14 trả lời

[Dark Repulsor]

Ngày $1$:

Bài $1$: Cho $x,y,z>0$ thỏa mãn $xyz=1$. Tìm max của bt: $P=\sum\frac{1}{x^2+2y^2+3}$

Bài $2$: Tìm tất cả các hàm số $f:\mathbb{R}\rightarrow\mathbb{R}$ đơn điệu trên $\mathbb{R}$ thỏa mãn:

                    $f(x^3+f(y))=f^3(x)+y$ $\forall x,y\in\mathbb{R}$

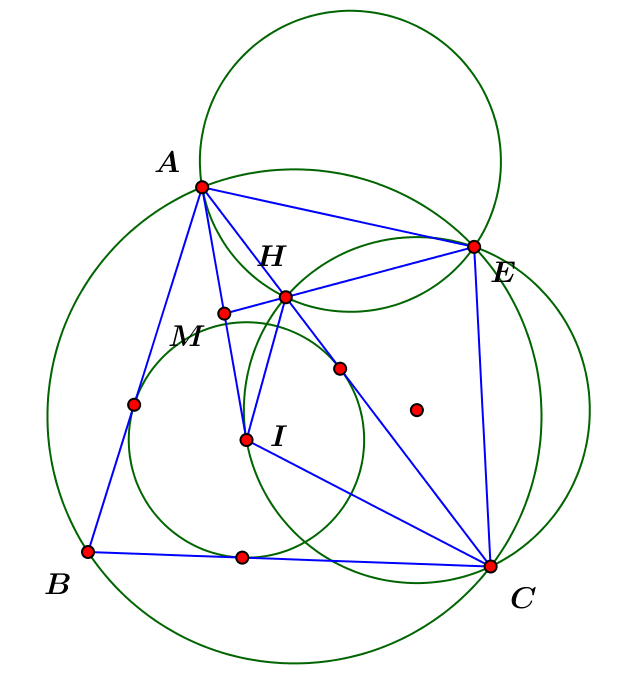
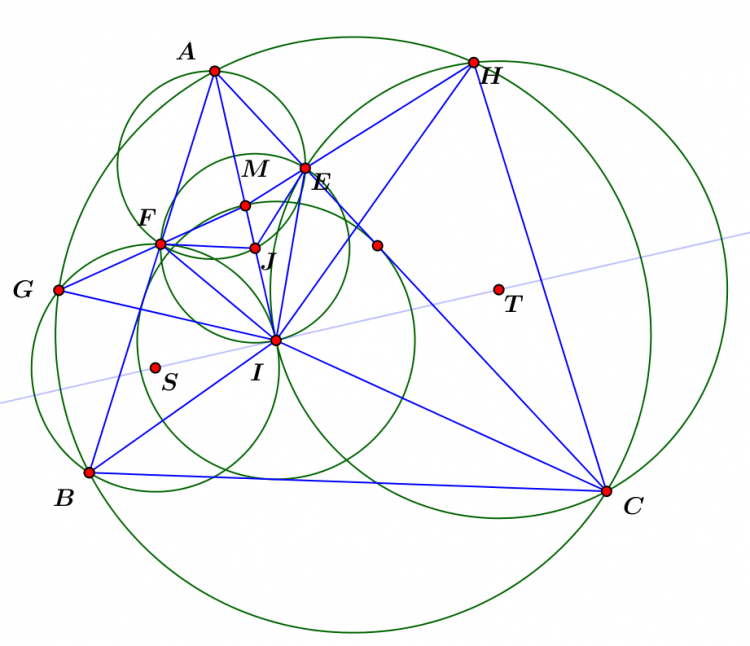
Bài $3$: Cho $\triangle ABC$ nhọn nội tiếp $(O)$ với $I$ là tâm nội tiếp tam giác. Đường tròn đi qua $C$ tiếp xúc với $AI$ tại $I$ cắt $AC$ tại $E$ và cắt $(O)$ tại $H$ $(E,H\neq C)$

$a)$ CMR: $EH$ đi qua trung điểm của $AI$ 

$b)$ Đường tròn đi qua $B$ tiếp xúc với $AI$ tại $I$ cắt $AB$ tại $F$ và cắt $(O)$ tại $G$ $(G,F\neq B)$. CMR: $2$ đường tròn $(EIF)$ và $(GIH)$ tiếp xúc nhau

Bài $4$: Cho đa thức $P(x)=4x^3-18x^2+27x+m$. CMR: Với mỗi $m\in\mathbb{Z}$, $\exists n\in\mathbb{Z}$ sao cho $P(n)\vdots 107$

 

Ngày $2$:

 

Bài $5$: Cho dãy số $(u_{n})$ xác định bởi: $\left\{\begin{matrix} & u_{1}=-\frac{1}{3} & \\ & u_{n+1}+1=\frac{u_{n}+1}{\sqrt{u_{n}^2+1}} & \end{matrix}\right.$ $\forall n\in\mathbb{N^{*}}$

$a)$ CMR: $u_{n+1}+1<\frac{3(u_{n}+1)}{\sqrt{10}}$ $\forall n\in\mathbb{N^{*}}$

$b)$ CMR: Dãy $(u_{n})$ hội tụ. Tính $\lim_{n\rightarrow +\infty} u_{n}$

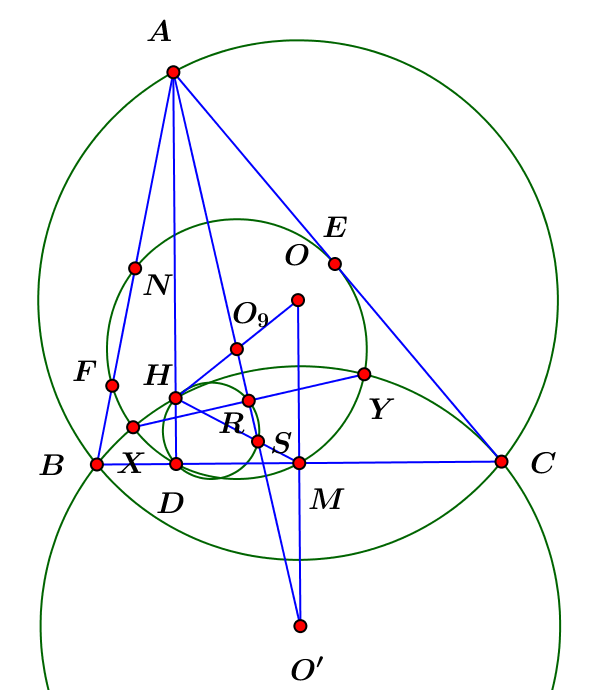
Bài $6$: Cho $\triangle ABC$ nhọn nội tiếp $(O)$. Các đường cao $AD,BE,CF$ cắt nhau ttai5 $H$ $(D\in BC,E\in CA,F\in AB)$. Gọi $M$ là trung điểm của $BC$. $2$ đường tròn $(DEF)$ và $(HBC)$ cắt nhau tại $X$ và $Y$

$a)$ CMR: $AX=AY$

$b)$ Gọi $R$ là trung điểm của $XY$. $AR$ cắt $HM$ tại $S$. CMR: Tứ giác $HDSR$ nội tiếp

Bài $7$: Cho tập $M_{n}=$ {$1;2;...;n$} $(n\in\mathbb{N^{*}})$ 

$a)$ Gọi $X$ là $1$ tập con của $M_{15}$ sao cho tích của $3$ ptử bất kỳ của $X$ ko phải số chính phương. Tìm max $\mid X\mid$

$b)$ Gọi $Y$ là $1$ tập con gồm có $15$ ptử của tập $M_{25}$. Tập $I'$ gọi là tập "tốt" nếu như ko tồn tại $2$ ptử nào mà tích của chúng là số chính phương. Tính số tất cả các tập "tốt" 

[NTMFlashNo1]

Ngày $1$:

Bài $1$: Cho $x,y,z>0$ thỏa mãn $xyz=1$. Tìm max của bt: $P=\sum\frac{1}{x^2+2y^2+3}$

 

 $P=\sum\frac{1}{x^2+2y^2+3}$

$\Leftrightarrow P=\sum \frac{1}{x^{2}+y^{2}+y^{2}+1+2}\leq \sum \frac{1}{2xy+2y+2}\leq \frac{1}{2}\sum \frac{1}{xy+y+1}$$\doteq \frac{1}{2}$

vì $\sum \frac{1}{xy+y+1}=1$

dấu"=" khi x=y=z=1

p/s:BĐT quá easy!!!!!!!!!!!!!

Bài viết đã được chỉnh sửa nội dung bởi NTMFlashNo1: 15-10-2016 - 21:08

[I Love MC]

Bài 4 : Ta chứng minh tồn tại $a,b$ để $4x^3-18x^2+27x+m=P(x) \equiv 4(x+a)^3+b=4x^3+12ax^2+12a^2x+b+4a^3 \pmod{107}$  
Chọn $a \in \mathbb{Z}$ sao cho $12a \equiv -18 \equiv 89 \pmod{107} \Rightarrow a \equiv 52 \pmod{107},(12,107)=1 \Rightarrow 12.52^2 \equiv 27 \pmod{107}$ 
Vậy với mọi $m$ ,chọn $b$ sao cho $b \equiv m-4a^3 \pmod{107}$ 

 

[IHateMath]

Câu 3.

a. Ta sẽ chứng minh rằng AI cũng là tiếp tuyến tại A của đường tròn (AHE). Thật vậy, trước hết có $\angle HIA=\angle HCI=1/2\angle ACB$. Từ đó $\angle HIC=\angle AIC-\angle AIH=90^{o}+1/2\angle ABC-1/2\angle ACB$. Măt khác, $\angle HEC=180^{o}-\angle HIC=90^{o}-1/2\angle ABC+1/2\angle ACB$ suy ra $\angle AEH=\angle AEC-\angle HEC=90^{o}-1/2\angle ABC-1/2\angle ACB=1/2\angle BAC=\angle IAH$ Vậy IA cũng là tiếp tuyến của (AHC). Tới đây thì theo tính chất của phương tích, ta phải có giao điểm của HE và AI (ta gọi là M) là trung điểm của AI.

Hình vẽ

[IHateMath]

Câu 3.

b. ta sẽ cm AI là đường nối tâm của (EIF) và (GIH). thật vậy, ta gọi giao của AI với (AEF) là J (khác A). Khi đó $\angle EJF=180^{o}-\angle BAC$, mà AI lại là phân giác góc EAF nên J là trung điểm cung EF của (AEF), hay JE=JF. Mà $\angle EIF=1/2\angle ABC+1/2\angle ACB=1/2(180^{o}-\angle BAC)$ và hơn nữa, IJ không phải là phân giác góc EIF nên J chính là tâm của (EIF) (1)

Gọi S, T lần lượt là tâm của (BIG) và (CIH). Bây giờ ta sẽ chỉ ra rằng (GIH) tiếp xúc với ST. Dễ thấy EF và GH là 2 đường đối song, vậy nên $\angle EFM=\angle GHM$. Ta có $\angle GIS=90^{o}-\angle GBI=90^{o}-\angle IFM=90^{o}-1/2\angle ABC-\angle JFM=90^{o}-1/2\angle ABC-\angle JFE+\angle MFE=90^{o}-1/2\angle ABC-1/2\angle BAC+\angle GHM=1/2\angle ACB+\angle HGM=\angle MHI+\angle MHG=\angle GHI$ suy ra ST là tiếp tuyến của (GIH) tại I, hay tâm của (GIH) thuộc AI. Từ đó có đpcm.

P/S: mình đánh nhầm tên các điểm E, H với nhau trong lời giải câu 3a. ở trên.

Hình vẽ

[IHateMath]

Câu 6

a. Đây là một kết quả khá cơ bản. Chỉ cần lấy O' đối xứng với O qua BC thì ta có O' là tâm (BHC), đồng thời dễ cm được AOO'H là hình bình hành, suy ra A, $O_9$ và O' thẳng hàng (ở đây $O_9$ chỉ tâm của đường tròn Euler (DEF)). Vậy hiển nhiên AX=AY.

b. Ta có AH.AD=AF.AB (phương tích của A tới (O). Ta có, mặt khác, AS:SO'=AH:MO'=AH:MO=2, do đó AS:AO'=2:3, suy ra $AS:AO_9=4:3$. Ta sẽ tính AR. Theo tính chất của phương tích, $RO'=\frac{O'O_9^2+R^2-R^{2}/4}{2O'O_9}=\frac{AO_9^2+3/4R^2}{2AO_9}$, suy ra $AR=AO'-RO'=2AO_9-\frac{AO_9^2+3/4R^2}{2AO_9}\Rightarrow AS.AR=4/3AO_9.\frac{3AO_9^2-3/4R^2}{2AO_9}=2AO_9^2-1/2R^2$. Ta lại có $AO_9^2-R^2/4=AF.AN=1/2AF.AB$ (N là trung điểm AB) nên $2AO_9^2-1/2R^2=AF.AB=AH.AD$, vậy nên AS.AR=AH.AD, suy ra HDSR nội tiếp một đường tròn (đpcm).

Hình vẽ

[dangkhuong]

Câu 3.

b. ta sẽ cm AI là đường nối tâm của (EIF) và (GIH). thật vậy, ta gọi giao của AI với (AEF) là J (khác A). Khi đó $\angle EJF=180^{o}-\angle BAC$, mà AI lại là phân giác góc EAF nên J là trung điểm cung EF của (AEF), hay JE=JF. Mà $\angle EIF=1/2\angle ABC+1/2\angle ACB=1/2(180^{o}-\angle BAC)$ và hơn nữa, IJ không phải là phân giác góc EIF nên J chính là tâm của (EIF) (1)

Gọi S, T lần lượt là tâm của (BIG) và (CIH). Bây giờ ta sẽ chỉ ra rằng (GIH) tiếp xúc với ST. Dễ thấy EF và GH là 2 đường đối song, vậy nên $\angle EFM=\angle GHM$. Ta có $\angle GIS=90^{o}-\angle GBI=90^{o}-\angle IFM=90^{o}-1/2\angle ABC-\angle JFM=90^{o}-1/2\angle ABC-\angle JFE+\angle MFE=90^{o}-1/2\angle ABC-1/2\angle BAC+\angle GHM=1/2\angle ACB+\angle HGM=\angle MHI+\angle MHG=\angle GHI$ suy ra ST là tiếp tuyến của (GIH) tại I, hay tâm của (GIH) thuộc AI. Từ đó có đpcm.

P/S: mình đánh nhầm tên các điểm E, H với nhau trong lời giải câu 3a. ở trên.

Hình vẽ

pic_2.png

Mình đã đăng một list bài như thế này trên blog của mình, bạn nào quan tâm có thể theo dõi

https://khuongworldo...n-tst-en-1.html

[khongcoten12]

Có cách nào dùng nghịch đảo cho ý b bai 6 k ak

Bài viết đã được chỉnh sửa nội dung bởi khongcoten12: 18-10-2016 - 21:05

[takarin1512]

Bài 7:

a.Chỉ ra tập $\left \{ 1,3,4,5,6,7,10,11,13,14 \right \}$ thỏa mãn yêu cầu đề bài. Giả sử tồn tại tập $X'$ có 11 phần tử thỏa mãn yêu cầu đề bài.

Trừ bỏ 2 phân tử 11 và 13 thì tập X có ít nhất 9 phần tử thuộc tập $M_{15}\setminus \left \{ 11,13 \right \}$.

Ta viết lại các phần tử của X dưới dạng số đó chia cho ước chính phương của nó, các số này có thể trùng nhau và chúng thuộc $\left \{ 2,3,5,7,6,10,14,15 \right \}=A$, số các số trong lần lượt trong tập A sẽ là 3,2,2,1,1,1,1,1,1.

_Nếu X chứa số 1: ta có được X chỉ có thể chứa tối đa 2 số 1, X không thể đồng thời chứa 2 số 2 hoặc 2 số 3. Do đó trong X có ít nhất 7 phần tử khác nhau thuộc tập $\left \{ 2,3,5,7,6,10,14,15 \right \}$, dễ thấy ngay điều này là vô lý.

_Nếu X không chứ số 1, do số 2 và số 3 xuất hiện tối đa 2 lần và các số kia chỉ xuất hiện 1 lần nên trong X có ít nhất 7 phần tử khác nhau thuộc tập $\left \{ 2,3,5,7,6,10,14,15 \right \}$, dễ thấy ngay điều này là vô lý.

Vậy $\left | X \right |_{max}=10$

b.TA cũng biến đổi các số tương tự câu a, ta thu được 16 số 1,2,3,5,6,7,10,11,13,14,15,17,19,21,22,23 với số lần xuất hiện lần lượt là 5,3,2,2,2,1,1,1,1,1,1,1,1,1,1,1. Dễ thấy nếu 2 số có cùng giá trị xuất hiện cùng nhau thì tích của chúng sẽ là 1 số chính phương do đó ta phải chọn 15 số khác nhau từ 16 số này. Do đó số tập "tốt" thỏa mãn là $5.3.2.2.2\left ( \frac{1}{5}+\frac{1}{3}+\frac{3}{2}+11 \right )=1564$

[khongcoten12]

Câu 6
a. Đây là một kết quả khá cơ bản. Chỉ cần lấy O' đối xứng với O qua BC thì ta có O' là tâm (BHC), đồng thời dễ cm được AOO'H là hình bình hành, suy ra A, $O_9$ và O' thẳng hàng (ở đây $O_9$ chỉ tâm của đường tròn Euler (DEF)). Vậy hiển nhiên AX=AY.
b. Ta có AH.AD=AF.AB (phương tích của A tới (O). Ta có, mặt khác, AS:SO'=AH:MO'=AH:MO=2, do đó AS:AO'=2:3, suy ra $AS:AO_9=4:3$. Ta sẽ tính AR. Theo tính chất của phương tích, $RO'=\frac{O'O_9^2+R^2-R^{2}/4}{2O'O_9}=\frac{AO_9^2+3/4R^2}{2AO_9}$, suy ra $AR=AO'-RO'=2AO_9-\frac{AO_9^2+3/4R^2}{2AO_9}\Rightarrow AS.AR=4/3AO_9.\frac{3AO_9^2-3/4R^2}{2AO_9}=2AO_9^2-1/2R^2$. Ta lại có $AO_9^2-R^2/4=AF.AN=1/2AF.AB$ (N là trung điểm AB) nên $2AO_9^2-1/2R^2=AF.AB=AH.AD$, vậy nên AS.AR=AH.AD, suy ra HDSR nội tiếp một đường tròn (đpcm).
Hình vẽ

pic_3.png

Có cách dùng nghch đảo cho ý b k ?

[dangkhuong]

Có cách dùng nghch đảo cho ý b k ?

bài này ko cần dùng nghịch đảo cx đc thì sao phải dùng hả bạn

[quantv2006]

Câu 6

a. Đây là một kết quả khá cơ bản. Chỉ cần lấy O' đối xứng với O qua BC thì ta có O' là tâm (BHC), đồng thời dễ cm được AOO'H là hình bình hành, suy ra A, $O_9$ và O' thẳng hàng (ở đây $O_9$ chỉ tâm của đường tròn Euler (DEF)). Vậy hiển nhiên AX=AY.

b. Ta có AH.AD=AF.AB (phương tích của A tới (O). Ta có, mặt khác, AS:SO'=AH:MO'=AH:MO=2, do đó AS:AO'=2:3, suy ra $AS:AO_9=4:3$. Ta sẽ tính AR. Theo tính chất của phương tích, $RO'=\frac{O'O_9^2+R^2-R^{2}/4}{2O'O_9}=\frac{AO_9^2+3/4R^2}{2AO_9}$, suy ra $AR=AO'-RO'=2AO_9-\frac{AO_9^2+3/4R^2}{2AO_9}\Rightarrow AS.AR=4/3AO_9.\frac{3AO_9^2-3/4R^2}{2AO_9}=2AO_9^2-1/2R^2$. Ta lại có $AO_9^2-R^2/4=AF.AN=1/2AF.AB$ (N là trung điểm AB) nên $2AO_9^2-1/2R^2=AF.AB=AH.AD$, vậy nên AS.AR=AH.AD, suy ra HDSR nội tiếp một đường tròn (đpcm).

Hình vẽ

pic_3.png

Gọi T là giao của EF và BC. TA cắt (O) tại N thì AN.AT = AH. AD = AR.AS

[Amateur of Mathematics]

$P=\sum\frac{1}{x^2+2y^2+3}$
$\Leftrightarrow P=\sum \frac{1}{x^{2}+y^{2}+y^{2}+1+2}\leq \sum \frac{1}{2xy+2y+2}\leq \frac{1}{2}\sum \frac{1}{xy+y+1}$$\doteq \frac{1}{2}$
vì $\sum \frac{1}{xy+y+1}=1$
dấu"=" khi x=y=z=1
p/s:BĐT quá easy!!!!!!!!!!!!!

Vì sao $\sum \frac{1}{xy+y+1}=1$

[thinhrost1]

Bài 4 : Ta chứng minh tồn tại $a,b$ để $4x^3-18x^2+27x+m=P(x) \equiv 4(x+a)^3+b=4x^3+12ax^2+12a^2x+b+4a^3 \pmod{107}$  
Chọn $a \in \mathbb{Z}$ sao cho $12a \equiv -18 \equiv 89 \pmod{107} \Rightarrow a \equiv 52 \pmod{107},(12,107)=1 \Rightarrow 12.52^2 \equiv 27 \pmod{107}$ 
Vậy với mọi $m$ ,chọn $b$ sao cho $b \equiv m-4a^3 \pmod{107}$ 

 

Có thể thay $107$ bởi $p=3k+2$ bất kì (p nguyên tố).

 

https://toanhocsocap...o-dang-3k2.html

[I Love MC]

Có thể thay $107$ bởi $p=3k+2$ bất kì (p nguyên tố).

 

https://toanhocsocap...o-dang-3k2.html

hmm đúng rồi nó xuất phát bổ đề sau 
Cho $p$ là số nguyên tố chia $3$ dư $2$ và $x,y$ nguyên dương . Ta có $x^3 \equiv y^3 \pmod{p} \Leftrightarrow x \equiv y \pmod{p}$