Chủ đề này có 13 trả lời

[PSW]

Ngày 15/04, trận đấu DELTA - GAMMA sẽ bắt đầu. BTC yêu cầu đội DELTA khẩn trương nộp đề

[PSW]

ĐỀ THI CỦA GAMMA:
 Đề Gama-Delta II.pdf   112.18K   423 Số lần tải
ĐỀ THI CỦA DELTA
 dethiDELTA.pdf   117.4K   420 Số lần tải

[perfectstrong]

Perfectstrong xin giải bài 4 của đội $\Delta$.
Lời giải 1:
Quy ước trong bài làm: "False" là "vô lý"
=================================================
Gọi số cần tìm là $\overline{abc}$ với $a,b,c \in \mathbb{N}$ và $0 \leq a;b;c \leq 9$ ($a \neq 0$).
Nếu trong 3 chữ số $a,b,c$ có ít nhất 2 số lớn hơn hoặc bằng 6 thì
\[ \overline{abc}=a!+b!+c! \geq 0!+6!+6!=1441: False \]
Suy ra, trong $a,b,c$ có nhiều nhất 1 số bằng 6.
Nếu $a=6$ thì
\[
\begin{array}{l}
\overline {abc} = \overline {6bc} = 6! + b! + c! = 720 + b! + c! \\
\overline {6bc} \le 655 \Rightarrow 720 + b! + c! \le 655:False \\
\end{array}
\]
Nếu $b=6$ thì
\[
\begin{array}{l}
\overline {abc} = \overline {a6c} = 6! + a! + c! = 720 + a! + c! \\
\overline {a6c} \le 565 \Rightarrow 720 + b! + c! \le 565:False \\
\end{array}
\]
Nếu $c=6$ thì
\[
\begin{array}{l}
\overline {abc} = \overline {ab6} = 6! + b! + a! = 720 + a! + c! \\
\overline {ab6} \le 556 \Rightarrow 720! + a! + b! \le 556:False \\
\end{array}
\]
Do đó, không có chữ số nào bằng 6. Nên $a;b;c \leq 5 \Rightarrow b!+c!\leq 2.5!=240$(*).
TH1:

\[
\begin{array}{l}
a = 5 \Rightarrow \overline {abc} = \overline {5bc} = 5! + b! + c! = 120 + b! + c! \\
\overline {5bc} \ge 500 \Rightarrow 120 + b! + c! \ge 500 \Rightarrow b! + c! \ge 480 > 240:False \\
\end{array}
\]
TH2:

\[
\begin{array}{l}
a = 4 \Rightarrow \overline {abc} = \overline {4bc} = 4! + b! + c! = 24 + b! + c! \\
\overline {4bc} \ge 400 \Rightarrow 24 + b! + c! \ge 400 \Rightarrow b! + c! \ge 376 > 240:False \\
\end{array}
\]
TH3:
\[
\begin{array}{l}
a = 3 \Rightarrow \overline {abc} = \overline {3bc} = 3! + b! + c! = 6 + b! + c! \\
\overline {3bc} \ge 300 \Rightarrow 6 + b! + c! \ge 300 \Rightarrow b! + c! \ge 294 > 240:False \\
\end{array}
\]
TH4:
\[
\begin{array}{l}
a = 2 \Rightarrow \overline {abc} = \overline {2bc} = 2! + b! + c! = 2 + b! + c! \\
\overline {2bc} \ge 200 \Rightarrow 2 + b! + c! \ge 200 \Rightarrow b! + c! \ge 198 \Rightarrow c! \ge 198-b! \\
\end{array}
\]
Nếu $b=5 \Rightarrow c! \ge 198-b!=78 \Rightarrow c=5$. Thử lại $\overline{abc}=255$ không thỏa.
Nếu $b \le 4 \Rightarrow c! \ge 198-b! \ge 198-4!=174$ : vô lý vì $c! \le 5!=120$.
TH5: $a=1$.
Nếu $b \le 4$ và $c \le 4 \Rightarrow \overline{abc}=1!+b!+c! \leq 1+4!+4!=49<100$ : vô lý.
Do đó, có 1 trong 2 chữ số $b;c$ bằng 5.
Nếu $b=5$. Thử chọn $c \in \left\{ {0;1;2;3;4;5} \right\}$ thì ta chọn được $c=5$ thỏa $\Rightarrow \overline{abc}=145$.
Nếu $c=5$. Thử chọn $b \in \left\{ {0;1;2;3;4;5} \right\}$ thì không có chữ số $b$ thỏa mãn.

Kết luận:
\[ \boxed{\overline{abc}=145} \]
=================================================
=================================================
Lời giải 2:
Quy ước trong bài làm: "False" là "vô lý"; "True" là "thỏa"
=================================================
Gọi số cần tìm là $\overline{abc}$ với $a,b,c \in \mathbb{N}$ và $0 \leq a;b;c \leq 9$ ($a \neq 0$).
Nếu trong 3 chữ số $a,b,c$ có ít nhất 2 số lớn hơn hoặc bằng 6 thì
\[ \overline{abc}=a!+b!+c! \geq 0!+6!+6!=1441: False \]
Suy ra, trong $a,b,c$ có nhiều nhất 1 số bằng 6.
Nếu $a=6$ thì
\[
\begin{array}{l}
\overline {abc} = \overline {6bc} = 6! + b! + c! = 720 + b! + c! \\
\overline {6bc} \le 655 \Rightarrow 720 + b! + c! \le 655:False \\
\end{array}
\]
Nếu $b=6$ thì
\[
\begin{array}{l}
\overline {abc} = \overline {a6c} = 6! + a! + c! = 720 + a! + c! \\
\overline {a6c} \le 565 \Rightarrow 720 + b! + c! \le 565:False \\
\end{array}
\]
Nếu $c=6$ thì
\[
\begin{array}{l}
\overline {abc} = \overline {ab6} = 6! + b! + a! = 720 + a! + c! \\
\overline {ab6} \le 556 \Rightarrow 720! + a! + b! \le 556:False \\
\end{array}
\]
Do đó, không có chữ số nào bằng 6. Nên $a;b;c \leq 5 \Rightarrow a!;b!;c!\leq 5!=120$(*).
Nếu cả 3 chữ số $a,b,c$ đều nhỏ hơn hoặc bằng 4 thì $\overline{abc} \leq 3.4!=72<100:False$.
Suy ra, trong 3 chữ số $a,b,c$ phải có 1 chữ số bằng 5.
TH1:
\[
\begin{array}{l}
a = 5 \Rightarrow \overline {abc} = \overline {5bc} = 5! + b! + c! = 120 + b! + c! \\
\overline {5bc} \ge 500 \Rightarrow 120 + b! + c! \ge 500 \Rightarrow b! + c! \ge 480 > 240:False \\
\end{array}
\]
TH2:
\[
\begin{array}{l}
b = 5 \Rightarrow \overline {abc} = \overline {a5c} = a! + c! + 5! \le 3.5! = 360 \Rightarrow a \in \left\{ {1;2;3} \right\} \\
*a = 1 \Rightarrow \overline {a5c} = \overline {15c} = 1! + 5! + c! = 121 + c! \\
\overline {15c} \ge 150 \Rightarrow 121 + c! \ge 150 \Rightarrow c! \ge 29 \Rightarrow c = 5 \Rightarrow \overline {abc} = 155:False \\
*a = 2 \Rightarrow \overline {a5c} = \overline {25c} = 2! + 5! + c! = 122 + c! \\
\overline {25c} \ge 250 \Rightarrow 122 + c! \ge 250 \Rightarrow c! \ge 128:False \\
*a = 3 \Rightarrow \overline {a5c} = \overline {35c} = 3! + 5! + c! = 126 + c! \\
\overline {35c} \ge 350 \Rightarrow 126 + c! \ge 350 \Rightarrow c! \ge 224:False \\
\end{array}
\]
TH3:
\[
\begin{array}{l}
c = 5 \Rightarrow \overline {abc} = \overline {ab5} = a! + b! + 5! = a! + b! + 120 \le 3.5! = 360 \Rightarrow a \in \left\{ {1;2;3} \right\} \\
*a = 1 \Rightarrow \overline {ab5} = \overline {1b5} = 1! + 5! + b! = 121 + b! \\
\end{array}
\]
Thử chọn $b \in \left\{ {0;1;2;3;4;5} \right\} \Rightarrow b = 4 \Rightarrow \overline {abc} = 145:True$
\[
\begin{array}{l}
*a = 2 \Rightarrow \overline {ab5} = \overline {2b5} = 2! + 5! + b! = 122 + b! \\
\overline {2b5} \ge 205 \Rightarrow 122 + b! \ge 205 \Rightarrow b! \ge 83 \Rightarrow b = 5 \Rightarrow \overline {abc} = 255:False \\
*a = 3 \Rightarrow \overline {ab5} = \overline {3b5} = 3! + 5! + b! = 126 + b! \\
\overline {3b5} \ge 305 \Rightarrow 126 + b! \ge 305 \Rightarrow b! \ge 179:False \\
\end{array}
\]
Kết luận:
\[ \boxed{\overline{abc}=145} \]

Bài viết đã được chỉnh sửa nội dung bởi perfectstrong: 23-04-2012 - 14:44

[tranghieu95]

tranghieu95 đội Delta xin giải bài 3 đội Gamma
Ta có:
$S=\sum \dfrac{1-x}{2x^2+(1-2)^2}$
Theo BĐT C-S ta có:
$[2x^2+(1-x)^2](1+2)\geq [\sqrt{2}x+\sqrt{2}(1-x)]^2=2
\Rightarrow \dfrac{1-x}{2x^2+(1-2)^2}\leq \dfrac{3}{2}(1-x)$
Tương tự với b và c ta được:
$S\leq\dfrac{3}{2}(1-x)+\dfrac{3}{2}(1-y)+\dfrac{3}{2}(1-z)=3$
Vậy ta có đpcm
(Dấu = khi và chỉ khi $x=y=z=\dfrac{1}{3}$)

Bài viết đã được chỉnh sửa nội dung bởi tranghieu95: 15-04-2012 - 08:52

[hoangtrong2305]

$hoangtrong2305$ đội $Delta$ giải bài $1$ của $Gamma$

Ta có: $(x+\sqrt{y^{2}+1})(y+\sqrt{x^{2}+1})=1$

Để chứng minh $(x+\sqrt{x^{2}+1})(y+\sqrt{y^{2}+1})=1$ là đúng, ta sẽ chứng minh hệ phương trình

$$\left\{\begin{matrix} (x+\sqrt{y^{2}+1})(y+\sqrt{x^{2}+1})=1\\ (x+\sqrt{x^{2}+1})(y+\sqrt{y^{2}+1})=1 \end{matrix}\right.$$

luôn đúng với mọi giá trị $x;y$

$\left\{\begin{matrix} (x+\sqrt{y^{2}+1})(y+\sqrt{x^{2}+1})=1(a)\\ (x+\sqrt{x^{2}+1})(y+\sqrt{y^{2}+1})=1(b) \end{matrix}\right.$

$\Leftrightarrow \left\{\begin{matrix} xy+x\sqrt{x^{2}+1}+y\sqrt{y^{2}+1}+\sqrt{x^{2}+1}.\sqrt{y^{2}+1}=1\\xy+x\sqrt{y^{2}+1}+y\sqrt{x^{2}+1}+\sqrt{x^{2}+1}.\sqrt{y^{2}+1}=1 \end{matrix}\right.$

$\Leftrightarrow x\sqrt{x^{2}+1}-x\sqrt{y^{2}+1}+y\sqrt{y^{2}+1}-y\sqrt{x^{2}+1}=0$

$\Leftrightarrow x(\sqrt{x^{2}+1}-\sqrt{y^{2}+1})-y(\sqrt{x^{2}+1}-\sqrt{y^{2}+1})=0$

$\Leftrightarrow (x-y)(\sqrt{x^{2}+1}-\sqrt{y^{2}+1})=0$

$\Leftrightarrow \begin{bmatrix} x=y\\ \sqrt{x^{2}+1}=\sqrt{y^{2}+1} \end{bmatrix}$

$\Leftrightarrow \begin{bmatrix} x=y\\ x^{2}+1=y^{2}+1 \end{bmatrix}$

$\Leftrightarrow \begin{bmatrix} x=y\\ x^{2}=y^{2} \end{bmatrix}$

$\Leftrightarrow \begin{bmatrix} x=y\\ x=-y \end{bmatrix}$


TRƯỜNG HỢP 1: $x=y$ (1)

Thay vào $(a)$:

$\Leftrightarrow (x+\sqrt{x^{2}+1})(x+\sqrt{x^{2}+1})=1$

$\Leftrightarrow (x+\sqrt{x^{2}+1})^{2}=1$

$\Leftrightarrow \begin{bmatrix} x+\sqrt{x^{2}+1}=1\\ x+\sqrt{x^{2}+1}=-1 \end{bmatrix}$

***Trường hợp $1.1$: $x+\sqrt{x^{2}+1}=1$

$\Leftrightarrow \sqrt{x^{2}+1}=1-x$

$\Leftrightarrow x^{2}+1=1-2x+x^{2}$

$\Leftrightarrow 2x=0$

$\Leftrightarrow x=0$

Thay vào $(1)\Rightarrow x=y=0$

***Trường hợp $1.2$: $x+\sqrt{x^{2}+1}=-1$

$\Leftrightarrow \sqrt{x^{2}+1}=-1-x$

$\Leftrightarrow x^{2}+1=1+2x+x^{2}$

$\Leftrightarrow 0=2x$


$\Leftrightarrow x=0$

Thay vào $(1)\Rightarrow x=y=0$




TRƯỜNG HỢP 2: $x=-y$

Thay vào $(a)$:

$\Leftrightarrow (\sqrt{y^{2}+1}-y)(\sqrt{y^{2}+1}+y)=1$

$\Leftrightarrow 1=1$ (đúng)

Vậy ở trường hợp này, hệ phương trình luôn đúng với mọi giá trị $x;y$

Do 2 trường hợp này chỉ xảy ra một trong hai, nên hoặc $(x;y)=(0;0)$ hoặc luôn đúng với mọi giá trị $x;y$

Vậy nếu giá trị $(x;y)$ thỏa mãn $(x+\sqrt{y^{2}+1})(y+\sqrt{x^{2}+1})=1$ thì cũng thỏa phương trình $(x+\sqrt{x^{2}+1})(y+\sqrt{y^{2}+1})=1$

Từ đó ta có điều phải chứng minh.

Bài viết đã được chỉnh sửa nội dung bởi hoangtrong2305: 15-04-2012 - 16:01

[anh qua]

anh qua của đội DELTA giải bài Olympiad của đội GAMA.
Đề bài: Chứng minh rằng: với mọi số nguyên dương $n > 2$ luôn tìm được số nguyên dương m sao cho $\phi(m+n)=\phi(m)$
Chứng minh:
Giả sử $n = p_{1}^{a_{1}}....p_{k}^{a_{k}} (p_{i}$ nguyên tố, $i= 1,2,..,k$)
Ta chọn m là số nguyên dương thỏa mãn các tính chất sau:
- $m = an$, a nguyên dương;
- $a + 1= p$ với p là số nguyên tố nhỏ nhất không là ước của n.
- $p - 1=p_{1}^{b_{1}}.p_{2}^{b_2}...p_{k}^{b_{k}}$ ( do cách chọn p)
Từ đố cộng với $\phi$ là hàm nhân tính ( cái này chắc không cần chứng minh ). Suy ra:\\
-$\phi(m+n)=\phi(p.n)=\phi(p).\phi(n)= (p-1).\phi(n). (1)$
-$\phi(m)=\phi((p-1)n) = \phi(p_{1}^{(a_1+b_1)}...p_{k}^{(a_k+b_k)})$
$ =p_{1}^{(a_1+b_1)}...p_{k}^{(a_k+b_k)}.(1- \frac{1}{p_{1})(1 - \frac{1}{p_2})...(1- \frac{1}{p_k}) $
Ta có Q.E.D
Và cuối cùng thật lòng xin lỗi Leader đội DELTA vì không nộp đề trận này!
@leader Gama: Đề của các cậu là đề về số học.
Anh em DELTA nao sua Latex ho cai!

Bài viết đã được chỉnh sửa nội dung bởi anh qua: 23-04-2012 - 18:53

[alex_hoang]

Êu ,GAMA thất thế như này rồi sao.Phải cố lên GAMA ơi
Bài 5:
Trước hết ta có$f(x) = \frac{1}{2}\ln ({x^2} + 1) - 2002$ là hàm số xác đinh trên $R$
$$f'(x) = \frac{x}{{{x^2} + 1}}$$
Bây giờ ta xét
$$g(x) = x + 2002 - \frac{1}{2}\ln (1 + {x^2})=x-f(x)$$
Vậy thì $g(x)$ cũng xác định trên $R$
Ta có
\[g'(x) = 1 - \frac{x}{{{x^2} + 1}} = \frac{{{x^2} - x + 1}}{{1 + {x^2}}} > 0\left( {\forall x \in R} \right)\]
Mà
\[g(0)g( - 2002) = - 1001\ln (1 + {2002^2}) < 0\]
Từ đó tồn tại $L \in \left( { - 2002,0} \right)$ mà $$g(L) = 0 \Rightarrow f(L) = L$$
Theo định lý Lagrange ta có tồn tại $c \in R$ sao cho
\[\left| {{U_{n + 1}} - L} \right| = \left| {f({u_n}) - f(L)} \right| = \left| {f'(c)} \right|\left| {{u_n} - L} \right| \le \frac{1}{2}\left| {{u_n} - L} \right|\]
Từ đó ta có
\[\frac{1}{2}\left| {{u_n} - L} \right| \le {\left( {\frac{1}{2}} \right)^{n - 1}}\left| {{U_1} - L} \right|\forall n \in N\]
Vậy
\[\mathop {\lim }\limits_{n \to + \infty } {u_n} = L\]

[alex_hoang]

Mong mọi người xem xét đề bài 6 của đội DELTA nhé $n$ thuộc $N$ và $n$ thuộc $N*$ nó khác nhau lắm.Nếu mà $n$ thuộc $N$ thì cho $n=0$ bài toán rất dễ còn nếu mà $n$ thuộc $N*$ thì ta phải biện luận số nghiêm tự nhiên của phương trình $$\frac{{p - 1}}{{{a_1}}} + \frac{p}{{{a_2}}} = 1$$
Mình nghĩ răng bài 6 này là $n$ thuộc $N*$ thì đúng hơn
Tạm thời mình post lời giải theo đề bài gốc có nghĩa là trường hợp $n$ thuộc $N$
\[{S_n} = \frac{{{a_0}}}{{{a_1}}} + \frac{{{a_0}}}{{{a_2}}} + ...... + \frac{{{a_0}}}{{{a_n}}} + \frac{p}{{{a_{n + 1}}}} \Rightarrow {S_{n + 1}} - {S_n} = 0 = \frac{p}{{{a_{n + 2}}}} - \frac{{p - {a_0}}}{{{a_{n + 1}}}}\]
Hay là
\[{a_{n + 2}} = \frac{p}{{p - {a_0}}}{a_{n + 1}}\]
Giả sử dãy số $a_0,a_1,...$ thoả mãn điều kiện bài toán khi đó với mọi $n \ge 3$ ta có
\[{a_n} = \frac{p}{{p - {a_0}}}{a_{n - 1}} = ..... = {\left( {\frac{p}{{p - {a_0}}}} \right)^{n - 2}}{a_2}\]
Dễ thấy $a_0$ thuộc $N$ vaf $p,p-a_0$ nguyên tố cùng nhau do $0<p-a_0<p$ nên số $a_2$ chia hết cho $(p-a_0)^{n-2}$ hay là $p-a_0=1$.Vậy ta có
\[{a_0} = p - 1;\frac{{p - 1}}{{{a_1}}} + \frac{p}{{{a_2}}} = 1;{a_n} = {p^{n - 2}}{a_2}(n \ge 3)\]
Mà khi $n=0$ thì
\[\frac{p}{{{a_1}}} = 1 \Rightarrow {a_1} = p\]
Nên $a_2=p^2$
Vậy dãy số trên là duy nhất bài toán được giải quyết

Bài viết đã được chỉnh sửa nội dung bởi alex_hoang: 23-04-2012 - 19:10

[perfectstrong]

Anh alex_Hoang trở lại rồi
Bài 2 của $\Delta$ có "vấn đề" gì thì phải?
Perfectstrong xing giải bài 2 của $\Delta$
Lời giải:

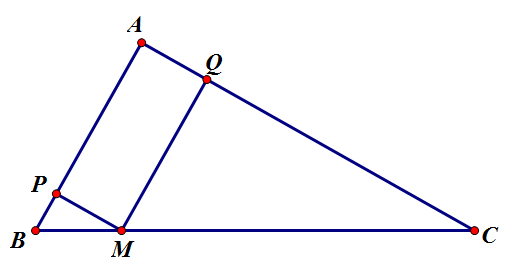
Câu trả lời là có. Chứng minh như sau:
$PM \perp AB$ và $AC \perp AB \Rightarrow PM \parallel AC$
Nên theo định lý Thales, ta có: $\dfrac{AC}{PM}=\dfrac{BC}{CM}$
Tương tự, $\dfrac{AB}{MQ}=\dfrac{BC}{BM}$
Xét
\[
\begin{array}{l}
\frac{1}{{BM}} + \frac{1}{{CM}} \ge \frac{2}{{\sqrt {BM.CM} }} \ge \frac{2}{{\frac{{BM + CM}}{2}}} = \frac{4}{{BC}} \\
\Rightarrow \frac{{AC}}{{PM}} + \frac{{AB}}{{QM}} = \frac{{BC}}{{CM}} + \frac{{BC}}{{BM}} \ge 4 \\
\end{array}
\]

[alex_hoang]

Trở lại gì em,anh vẫn online trên diễn đàn mà nhưng do phải ôn đại học nên ít ghé vào đấu trường thôi.Nay vừa thi thử ĐH xong nên ghé qua giúp đỡ đội GAMA tí.Phải mong chờ hai cao thủ LeVietThai và HoangKHTN của đội ta thôi:))

[perfectstrong]

Trở lại gì em,anh vẫn online trên diễn đàn mà nhưng do phải ôn đại học nên ít ghé vào đấu trường thôi.Nay vừa thi thử ĐH xong nên ghé qua giúp đỡ đội GAMA tí.Phải mong chờ hai cao thủ LeVietThai và HoangKHTN của đội ta thôi:))

Nguyễn Thái Phúc chứ anh. LeVietThai có ở đội mình đâu

Bài viết đã được chỉnh sửa nội dung bởi perfectstrong: 23-04-2012 - 20:58

[alex_hoang]

Bài 4:
Gọi $G$ là giao điểm của $DM$ và mặt phẳng $(ABC)$ .Ta dễ suy ra được $G$ là trọng tâm của tam giác $ABC$
Ta có
\[\overrightarrow {DA} + \overrightarrow {DB} + \overrightarrow {DC} = 3\overrightarrow {DG} \Rightarrow \frac{{DA}}{{DA'}}\overrightarrow {DA'} + \frac{{DB}}{{DB'}}\overrightarrow {DB'} + \frac{{DC}}{{DC'}}\overrightarrow {DC'} = 3.\frac{4}{3}\overrightarrow {DM} = 4\overrightarrow {DM} \]
Do các điểm $A';B';C'$ đồng phẳng nên ta có
\[\frac{{DA}}{{DA'}} + \frac{{DB}}{{DB'}} + \frac{{DC}}{{DC'}} = 4\]
\[ \Rightarrow \frac{{{\rm{AA}}'}}{{DA'}} + \frac{{BB'}}{{DB'}} + \frac{{CC'}}{{DC'}} = 1\]
Mà
\[T = {V_{AB'C'D'}} + {V_{BA'B'C'}} + {V_{CA'B'C'}} = {V_{DA'B'C'}}\left( {\frac{{{\rm{AA}}'}}{{DA'}} + \frac{{BB'}}{{DB'}} + \frac{{CC'}}{{DC'}}} \right) = {V_{DA'B'C'}}\]
Mặt khác theo BĐT $AM-GM$ thì
\[4 = \frac{{DA}}{{DA'}} + \frac{{DB}}{{DB'}} + \frac{{DC}}{{DC'}} \ge 3\sqrt[3]{{\frac{{DA}}{{DA'}}\frac{{DB}}{{DB'}}\frac{{DC}}{{DC'}}}} \Rightarrow \frac{{DA'.DB'.DC'}}{{DA.DB.DC}} \ge \frac{{27}}{{64}}\]
Do đó
\[\frac{{{V_{DA'B'C'}}}}{{{V_{DACB}}}} = \frac{{DA'.DB'.DC'}}{{DA.DB.DC}} \ge \frac{{27}}{{64}}\]
Từ đó ta có
\[T \ge \frac{{27}}{{64}}V\]
Dấu bằng xảy ra khi $(A'B'C')$ song song với $(ABC)$

Bài viết đã được chỉnh sửa nội dung bởi alex_hoang: 23-04-2012 - 21:16

[alex_hoang]

Trở lại gì em,anh vẫn online trên diễn đàn mà nhưng do phải ôn đại học nên ít ghé vào đấu trường thôi.Nay vừa thi thử ĐH xong nên ghé qua giúp đỡ đội GAMA tí.Phải mong chờ hai cao thủ LeVietThai và HoangKHTN của đội ta thôi:))

Nguyễn Thái Phúc chứ anh. LeVietThai có ở đội mình đâu

Chán anh thật xin lỗi mọi người Hì thành viên trong đội mà còn nhớ sai tên:((
P/s Hân ơi sao lần này đề đội GAMA có vè hơi nhẹ thì phải em ạ

Bài viết đã được chỉnh sửa nội dung bởi alex_hoang: 23-04-2012 - 21:20

[Dung Dang Do]

anh qua của đội DELTA giải bài Olympiad của đội GAMA.
Đề bài: Chứng minh rằng: với mọi số nguyên dương $n > 2$ luôn tìm được số nguyên dương m sao cho $\phi(m+n)=\phi(m)$
Chứng minh:
Giả sử $n = p_{1}^{a_{1}}....p_{k}^{a_{k}} (p_{i}$ nguyên tố, $i= 1,2,..,k$)
Ta chọn m là số nguyên dương thỏa mãn các tính chất sau:
- $m = an$, a nguyên dương;
- $a + 1= p$ với p là số nguyên tố nhỏ nhất không là ước của n.
- $p - 1=p_{1}^{b_{1}}.p_{2}^{b_2}...p_{k}^{b_{k}}$ ( do cách chọn p)
Từ đố cộng với $\phi$ là hàm nhân tính ( cái này chắc không cần chứng minh ). Suy ra:\\
-$\phi(m+n)=\phi(p.n)=\phi(p).\phi(n)= (p-1).\phi(n). (1)$
-$\phi(m)=\phi((p-1)n) = \phi(p_{1}^{(a_1+b_1)}...p_{k}^{(a_k+b_k)})$
$$=p_{1}^{(a_1+b_1)}...p_{k}^{(a_k+b_k)}.(1- \frac{1}{p_{1})(1 - \frac{1}{p_2})...(1- \frac{1}{p_k}}) $$
Ta có Q.E.D
Và cuối cùng thật lòng xin lỗi Leader đội DELTA vì không nộp đề trận này!
@leader Gama: Đề của các cậu là đề về số học.
Anh em DELTA nao sua Latex ho cai!

Em người ngoài sửa chắc k sao anh nhỉ.
Anh coi đúng chưa nha