Đề của MSS01 - BlackSelena:
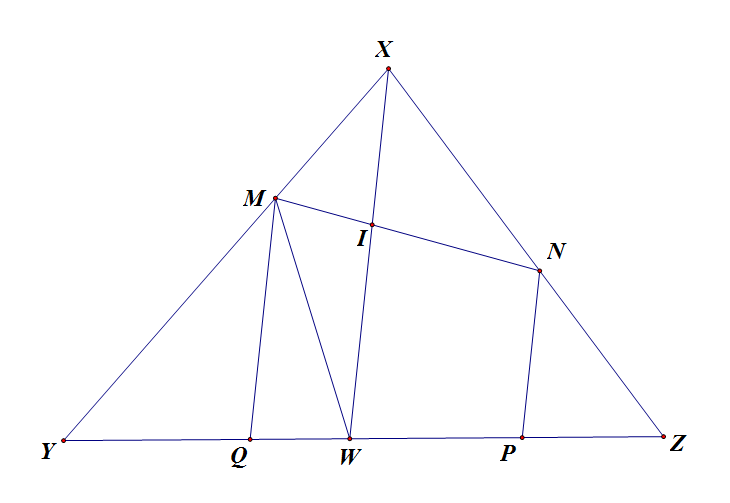
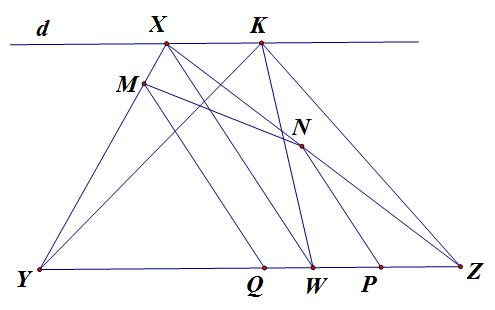
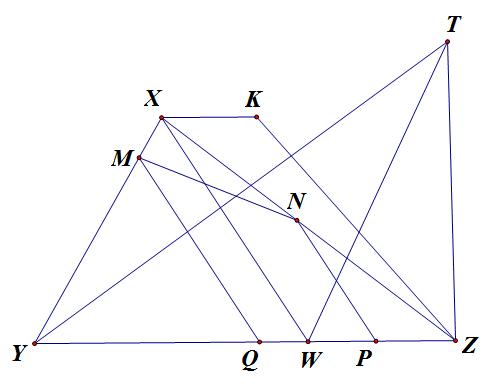
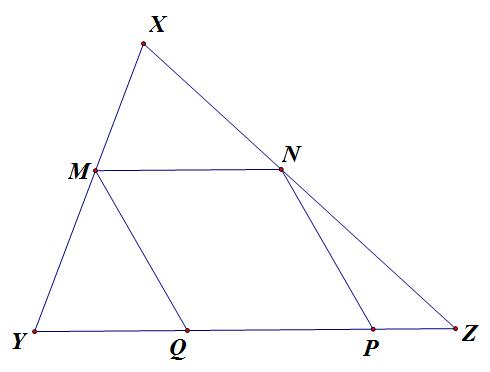
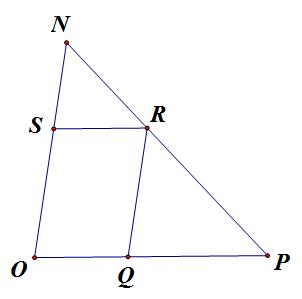
Cho $\triangle XYZ$, $W$ là điểm thuộc cạnh $YZ$. Trên $XY$ và $XZ$ lần lượt lấy các điểm $M$ và $N$. Các đường thẳng qua $M$ và $N$ song song với $XW$ cắt $YZ$ tại $Q$ và $P$. CMR:
$$S_{PMQN} \leq max \begin{Bmatrix} S_{XYW},S_{XZW} \end{Bmatrix}$$
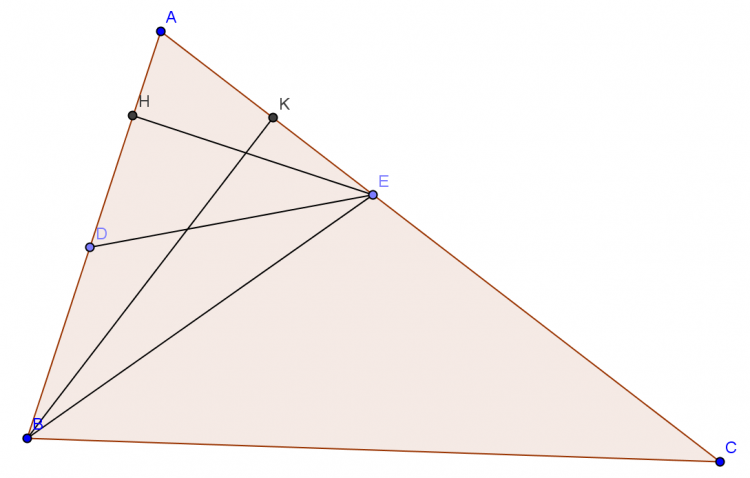
Bổ đề 1: Cho $\triangle{ABC}$; $D,E$ lần lượt nằm trên cạnh $AB,AC$. CMR: $\frac{S_{ADE}}{S_{ABC}}=\frac{AD.AE}{AB.AC}$.
 Chứng minh:
Chứng minh: $\triangle{ADE}$ và $\triangle{AEB}$ có chung đường cao $EH \Rightarrow \frac{S_{ADE}}{S_{AEB}}=\frac{AD}{AB}\; (1)$.
$\triangle{AEB}$ và $\triangle{ABC}$ có chung đường cao $BK \Rightarrow \frac{S_{AEB}}{S_{ABC}}=\frac{AE}{AC}\; (2)$.
Từ $(1),(2) \Rightarrow \frac{S_{ADE}}{S_{ABC}}=\frac{AD.AE}{AB.AC}$.
Bổ đề 2: Cho $\triangle{ABC}\sim \triangle{A'B'C'}$. CMR: $\frac{S_{ABC}}{S_{A'B'C'}}=\frac{AB^2}{A'B'^2}$.
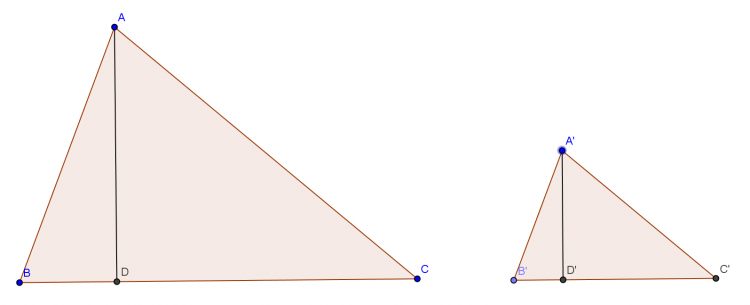
Chứng minh: Hạ đường cao $AD, A'D'$.
$\triangle{ABC}\sim \triangle{A'B'C'}\Rightarrow \widehat{ABC}=\widehat{A'B'C'}$ và $\frac{AB}{A'B'}=\frac{BC}{B'C'}\; (1)$
$\Rightarrow \triangle{ABD}\sim \triangle{A'B'D'}\; (g.g)\Rightarrow \frac{AB}{A'B'}=\frac{AD}{A'D'}\; (2)$.
Từ $(1);(2)\Rightarrow \frac{S_{ABC}}{S_{A'B'C'}}=\frac{AD.BC}{A'D'.B'C'}=\frac{AB}{A'B'^2}$.
Quay trở lại bài toán:
Giả sử $max \begin{Bmatrix} S_{XYW},S_{XZW} \end{Bmatrix}=S_{XYW}\Rightarrow S_{XYZ}\leq 2S_{XYW}$.
Đặt $YM=a; ZN=b; XY=x; ZX=y$.
Áp dụng bổ đề 2, ta có: $\frac{S_{YMQ}}{S_{YXW}}=\frac{a^2}{x^2}$ và $\frac{S_{ZNP}}{S_{ZXW}}=\frac{b^2}{y^2}$.
Áp dụng bổ đề 1, ta có: $\frac{S_{XMN}}{S_{XYZ}}=\frac{XM.XN}{XY.XZ}=\frac{(x-a)(y-b)}{xy}=1-\frac{a}{x}-\frac{b}{y}+\frac{ab}{xy}$
$\Rightarrow S_{MNPQ}=S_{XYZ}-S_{YMQ}-S_{ZNP}-S_{XMN}$
$=S_{XYW}+S_{XZW}-\frac{a^2}{x^2}S_{XYW}-\frac{b^2}{y^2}S_{XZW}-(1-\frac{a}{x}-\frac{b}{y}+\frac{ab}{xy})(S_{XYW}+S_{XZW})$
$=(1-\frac{a^2}{x^2}-1+\frac{a}{x}+\frac{b}{y}-\frac{ab}{xy})S_{XYW}+(1-\frac{b^2}{y^2}-1+\frac{a}{x}+\frac{b}{y}-\frac{ab}{xy})S_{XZW}$
$=(\frac{a}{x}+\frac{b}{y}-\frac{a^2}{x^2}-\frac{ax}{by})S_{XYW}+(\frac{a}{x}+\frac{b}{y}-\frac{b^2}{y^2}-\frac{ax}{by})S_{XZW}$
$\le [2(\frac{a}{x}+\frac{b}{y})-\frac{a^2}{x^2}-\frac{b^2}{y^2}-2\frac{ab}{xy}]S_{XYW}$.
Phải c/m: $S_{MNPQ}\le S_{XYW}$
$\Leftrightarrow 2(\frac{a}{x}+\frac{b}{y})-\frac{a^2}{x^2}-\frac{b^2}{y^2}-2\frac{ab}{xy}\le 1$
$\Leftrightarrow (\frac{a}{x}+\frac{b}{y}-1)^2\le 0$.
Bất đẳng thức cuối hiển nhiên đúng.
Dấu đẳng thức xảy ra $\Leftrightarrow \left\{\begin{matrix}
\frac{a}{x}+\frac{b}{y}=1\\
S_{XYW}=S_{XZW}
\end{matrix}\right.$
$\Leftrightarrow \frac{YM}{XY}+\frac{ZN}{XZ}=1$ và $W$ là trung điểm $YZ$.
Kết luận: Vậy $S_{PMQN} \leq max \begin{Bmatrix} S_{XYW},S_{XZW} \end{Bmatrix}$. Dấu đẳng thức xảy ra $\Leftrightarrow \frac{YM}{XY}+\frac{ZN}{XZ}=1$ và $W$ là trung điểm $YZ$.
====Điểm bài làm: 10Tổng điểm: $S = \left [\frac{52 - \left (6 - 5 \right )}{2} \right ]+3*10+0+0=55$
Bài viết đã được chỉnh sửa nội dung bởi Dramons Celliet: 31-10-2012 - 21:31


 Chủ đề bị khóa
Chủ đề bị khóa