Lời giải bài 1 của em:
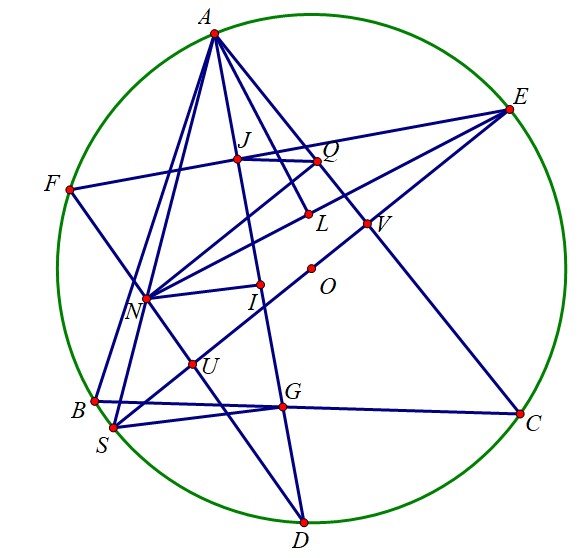
Như trên hình, em chỉ xét những điểm liên quan đến $N$.
Gọi $S, D$ lần lượt là điểm chính giữa cung $ABC, BC$ của $(O)$. Gọi $V$ là trung điểm $AC$ và $SE$ cắt $DF$ tại $U$. Gọi $AI$ cắt $BC$ tại $G$. Gọi $J$ là trung điểm của $AI$
Bằng cách định nghĩa ta dễ có: $N\in AS$
Nhận xét 1: $NQ$ vuông góc $AC$.
Chứng minh: Điều này tương đương với $NQ//SV$ hay theo định lý Ta-lét, ta cần chứng minh:
$\frac{AN}{AS}=\frac{AQ}{AV}$. Do: $\frac{AQ}{AV}=\frac{AI}{AG}$ dựa trên $JQ//AC$ và $J,V$ lần lượt là trung điểm của $AI,AC$.
Do đó, ta cần chứng minh: $\frac{AN}{AS}=\frac{AI}{AG}\Leftrightarrow\frac{NA}{NS}=\frac{IA}{IG}$, luôn đúng.
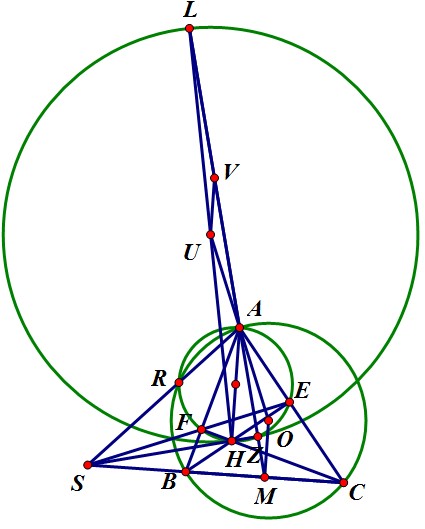
Nhận xét 2: $AP$ là đường đối trung trong tam giác $\Delta RAQ$.
Ta chứng minh điều này dựa vào định lý Ceva-sin.
Ta tính được: $\frac{\text{sin}\widehat{LQR}}{\text{sin}\widehat{LQA}}=\text{cos}(\frac{A}{2}).\frac{\text{cos}(\frac{C}{2})}{\text{sin}(\frac{B}{2})}$ $(1)$
Thiết lập, tương tự, ta có: $\frac{\text{sin}\widehat{KRA}}{\text{sin}\widehat{KRQ}}=1:\text{cos}(\frac{A}{2}).\frac{\text{sin}(\frac{C}{2})}{\text{cos}(\frac{B}{2})}$.
Nhân lại, sử dụng định lý sin và định lý Ceva-sin, ta có ngay:
$\frac{\text{sin}\widehat{RAP}}{\text{sin}\widehat{QAP}}=\frac{\text{sin}\widehat{AQR}}{\text{sin}\widehat{ARQ}}$, đủ để suy ra nhận xét.
Do đó, ta chứng minh $(1)$.
Cuối cùng, vì $AP$ là đường đối trung tam giác $RAQ$ nên cũng là đối trung tam giác $ABC$ nên đi qua điểm cố định là giao hai tiếp tuyến tại $B,C$ của $(O)$. $\blacksquare$
- yeutoan2001 yêu thích



 Tìm kiếm
Tìm kiếm Nam
Nam















 Gửi bởi
Gửi bởi