ecchi123

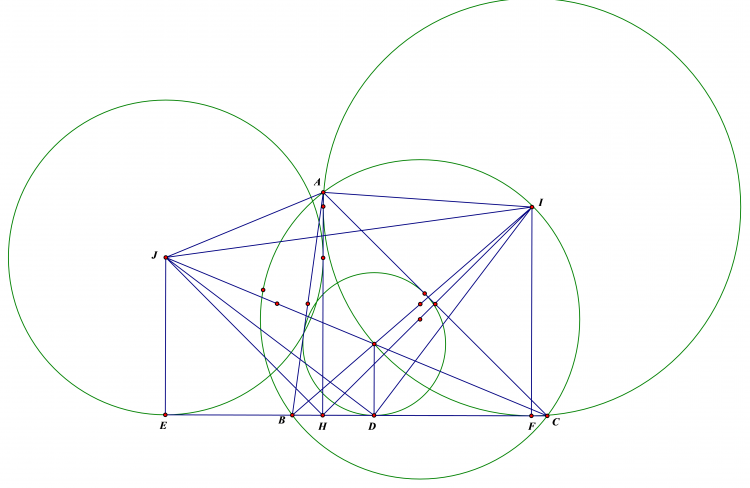
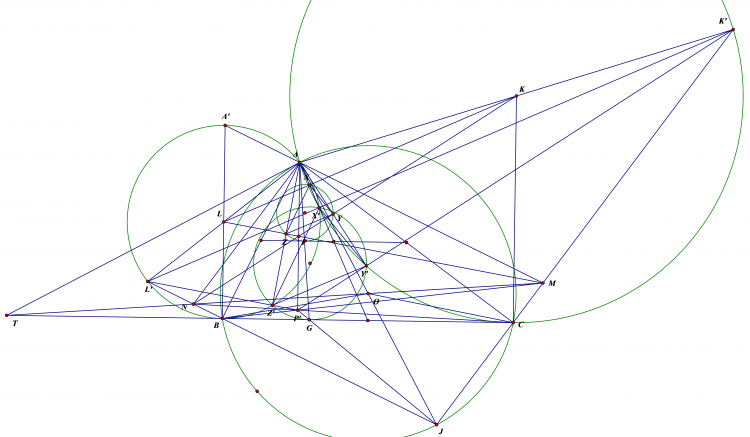
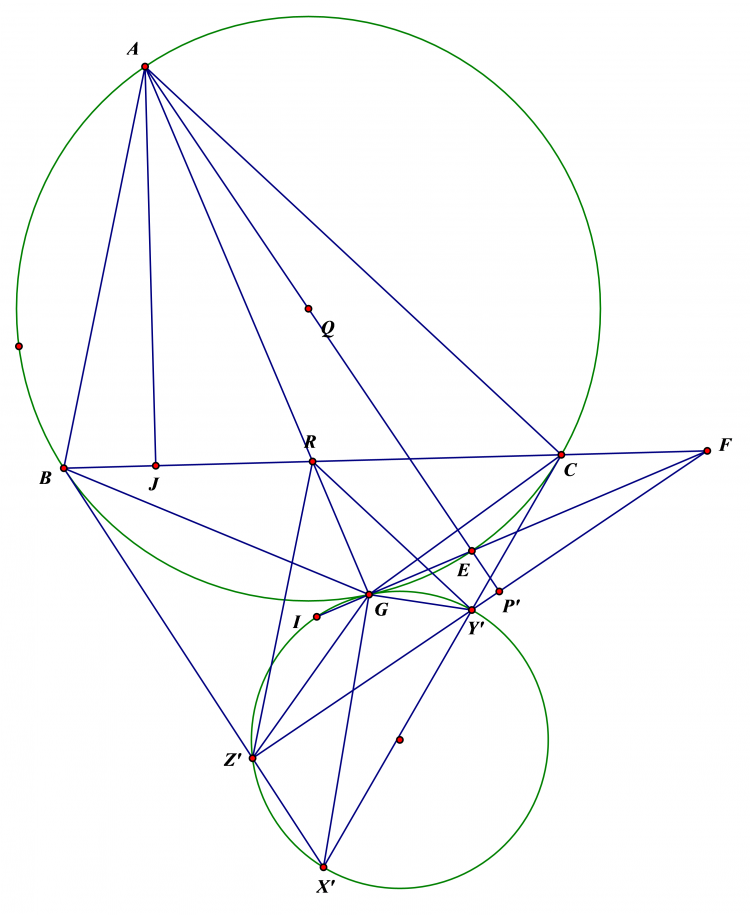
Lời giải bài 1 :

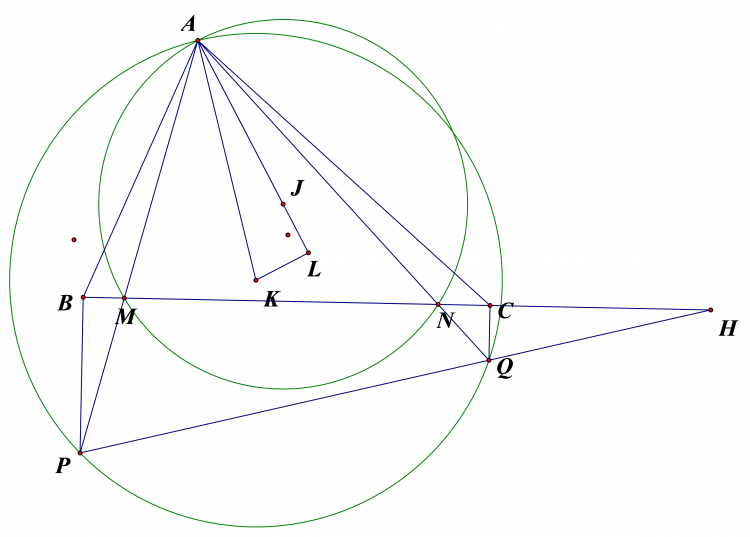
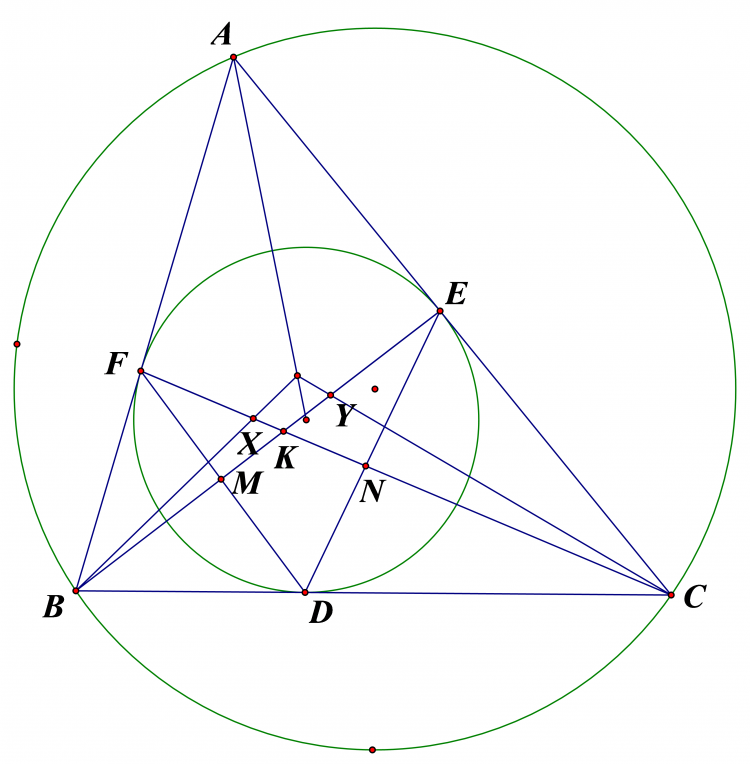
Gọi $PQ$ cắt $BC$ tại $H$ , ta có $\frac{AJ}{MN}=\frac{1}{2.sinMAN}=\frac{AK}{PQ}$

Mặt khác $\widehat{KAL}=\widehat{LAM}-\widehat{KAM}=\widehat{AQP}-\widehat{ANM}=\widehat{CHQ}$ nên $\frac{AK}{AL}=\frac{HQ}{HC}=\frac{PQ}{BC}$

Vậy $\frac{AJ}{MN}=\frac{AK}{PQ}=\frac{AL}{BC}$

Lời giải bài 1 :

Dễ dàng thấy $ANDY,AMDZ$ nội tiếp . Gọi $(AND)$ cắt $BC,BA$ tại $T,K$ . $(ADM)$ cắt $BC,AC$ tại $S,H$

Hạ đường cao $DP,DQ$ xuống $AB,AC$ ta có $EH.EA=EM.ED=EP.EC=>\frac{EA}{EC}=\frac{EP}{EH}=\frac{EA+EP}{EC+EH}=\frac{AP}{HC}$

Tương tự suy ra $\frac{AQ}{KB}=\frac{AF}{FB}=\frac{AE}{EC}=\frac{AP}{HC}$ nên $CH=BK$

Từ đó $\frac{CS}{CH}=\frac{CA}{CD}=\frac{BA}{BD}=\frac{BT}{BK}$ nên $CS=BT$ nên $BS=CT$

Vậy $\frac{BS}{BZ}=\frac{BA}{BD}=\frac{CA}{CD}=\frac{CT}{CY}$ nên $BZ=CY$

Lời giải bài 2 :

Giả sử $K,L$ là giao của $BH,CH$ với $EF$ . Ta sẽ chứng minh $K,L$ là trực tâm $MDE,MDF$ và thuộc $(H,HM)$

Thật vậy,$DM$ cắt $EF$ tại $N$ . $AI$ cắt $(O)$ tại $G$

Ta có $\triangle CLE \sim \triangle BKF$ và $\widehat{FBN}=\widehat{ECN}$ ( do $N(CBEN)=-1$ nên $ND$ là phân giác $BNC$ ) suy ra $\frac{NE}{NL}=\frac{NF}{NK}=>\frac{NL}{NK}=\frac{NE}{NF}=\frac{DC}{DB}$

Mà $\triangle GBC \sim \triangle HKL$ và $\widehat{IGB}=\widehat{MHK}$ và $\frac{NK}{NL}=\frac{DB}{DC}$ ,dựng vuông góc từ $D,N$ với $BC,EF$ cắt $GI,HM$ tại $I,H$ nên ta có hình $MKHL \sim IBGC => HK=HM=HL$

Từ đó $K,L$ thuộc $(H,HM)$

Mặt khác $\widehat{KMD}=\widehat{BID}=\widehat{GIC}$ nên $MK \parallel IC \perp ED$ từ đó $K$ là trực tâm $DME$ . tương tự với $L$ ta có dpcm

Lời giải bài 1 :

 Hạ $PX,PY$ xuống $AB,AC$ Ta có $ \Delta PXF\sim \Delta PYC ,\Delta PXB\sim \Delta PYE =>XF.YC=PY.PX=BX.YE =>\frac{XF}{XB}=\frac{YE}{YC} $  nên $(ABC),(AEF),(AXY)$ đồng trục  nên $(AEF)$ cắt $(O)$ tại $S$ thì góc $ASP$ vuông

 Ta chứng minh $S$ cũng nằm trên $(D,DP)$

Gọi $T$ là trung điểm $AP$ ,

Thật vậy , Ta có : $(LA,LD)=(OH,KP)=(QA,QD)$ nên $ALDQ$ nội tiếp  . Gọi $AL$ cắt $BC$ tại $G$ suy ra $AGQ,LGD$ cân tại $A,D$

 GỌi $U,I,J,Z$ là trung điểm của $PQ,LG,LA,AG$ . đường thẳng qua $A,Z$ vuông góc với $AG$ lần lượt cắt  $UO$ tại $N,M$ . $ZM$ cắt $BC$ tại $V$.

- Do các trung điểm nên $\widehat{ZTU}=180-\widehat{AQG}=180-\widehat{AGQ}=\widehat{ZMU} $ nên  $TMUZ$ nội tiếp suy ra $\widehat{UTM}=\widehat{UZM}=\widehat{UGM}=>$ $TMUG$ nội tiêp nên $ \widehat{GTM}=90$

- Tiếp tục , Ta có $\frac{NM}{TU}=\frac{NM}{AQ/2}=\frac{NM}{AZ}=\frac{1}{cos\widehat{NMZ}}=\frac{VM}{VU}=>\frac{MN}{MV}=\frac{UT}{UV}$ và $\widehat{TUG}=\widehat{AQG}=\widehat{UMV}$ nên $\Delta VMN \sim \Delta VUT$ nên $\Delta VMU \sim \Delta VNT$ nên $\widehat{VTN}=90$

Tóm lại $(UGM),(UNV)$ cùng đi qua $T$

 Ta lại có :$\frac{DG}{DV}=\frac{IG}{IZ}=\frac{JZ}{JA}=\frac{OM}{ON}$ nên $(UGM),(UNV), (UOD)$ đồng trục , từ đo $(UOD)$ cũng đi qua $T$ , tức là  $DT$ vuông $TO$ . mà $TO$ song song $PS$ vì cùng vuông với $AS$ và $TS=TP$ . suy ra $DS=DP$ nên $S$ thuộc $(D,DP)$

 Mặt khác , $\widehat{ESP}=\widehat{ESA}+90=EFA+90=\widehat{BAO}+90 =180-\widehat{ACB}$ nên $ESPC$ nội tiếp

Từ đó $180=\widehat{SPD}+\widehat{SAF}+\widehat{FSA}=\widehat{SPD}+\widehat{SAF}+90-\widehat{FSP}=>\widehat{FSP}=\widehat{FES}+\frac{\widehat{SDP}}{2}$

 Goi $Sx$ tiếp xúc với $(D)$ thì $Sx$ cũng tiếp xúc với $(AEF)$ do góc ở trên  

Từ đó $(AEF)$ tiếp xúc $(D,DP)$ tại $S$

Cho tam giác ABC ngoại tiếp (I). (I) tiếp xúc BC, CA, AB tại D,E, F. BE cắt DF tại M, CF cắt DE tại N. X, Y là trung điểm NF, ME. Cmr BX, CY và IA đồng quy

 $BE$ cắt $CF$ tại $K$=>$\frac{XN}{XC}=\frac{FK}{FC}$ theo maclaurint

 tương tự suy ra$\frac{XF}{XC}.\frac{YB}{YE}=\frac{FK}{FC}.\frac{EB}{EK}=\frac{DC}{DB}=>\frac{XF}{XC}:\frac{BF}{BC}=\frac{YE}{YB}:\frac{CE}{CB}$ => $B(XCIF)=C(YBIE)$ từ đó $BX,CY$ cắt nhau trên $AI$

Em học hình còn kém nên xin thắc mắc một số chỗ:

-Ở $(1)$, tại sao $\widehat{FBP}=\widehat{QBC}$?

-Ở $(2)$, tại sao $PQ$ song song $XY$ thì $AD$ chia đôi $PQ$?

-Ở $(3)$, tại sao $\widehat{YQC}=\widehat{FPX}$?

-Ở $(4)$, tại sao $\angle YBC=\angle FPX, \angle ABC+ \angle FPX=180-\angle XPC$

-Ở $(5)$, là theo đinh lí hay tính chất gì?

 

Em xin cảm ơn! 

(1) do $Q,P$ đẳng giác trong tam giác

(2) Định lí menelaus

(3) do 2 tam giác đồng dạng mình đã cm ở trên

(4) cái này cũng do tam giác đồng dạng $ABY$ và $APC$ làm tương tự , đoạn này bạn dể hiểu cộng cung $(PBC)$

(5) định lí về hàng điểm

Lời giải  bài 2 :

 Gọi $(BPC),(QBC)$ cắt $AB$ tại $F,E$ Có $\widehat{FXP}=\widehat{FBP}=\widehat{QBC}=\widehat{QYC}$ nên $ \Delta  AFX \sim \Delta ACY$ . từ đó $\frac{AX}{AY}=\frac{AF}{AC}$

Mặt khác $\widehat{AFP}=\widehat{PCB}=\widehat{QCA}$ nên  $ \Delta  AFP \sim \Delta ACQ$ từ đó $\frac{AP}{AQ}=\frac{AF}{AC}$

 Suy ra dc $PQ$ song song $XY$ , nên $AD$ chia đôi $PQ$

Giờ ta cm $D$ thuộc $BC$

 Gọi $ AP,AQ$ cắt $BC$ tại $M,N$

Ta có $ \widehat{YQC}=\widehat{FPX}    ,     \widehat{FBP}=\widehat{QBC}   ,     \widehat{QBE}=180-\widehat{ABQ}=180-\widehat{PBC}   ,       \widehat{YBA}=\widehat{YBC}+\widehat{ABC}=\widehat{ABC}+\widehat{FPX}=180-\widehat{XPC}$

nên 2 tứ giác $PFXC,QCYE$ đồng dạng với nhau nên $B(PFXC)=B(QCYE) => (PAXM)=(QNYA)=(YAQN)$ . từ đó $MN,PY,QX$ đồng quy

 Lời giải bài 1 :

Diều cần Cm tường đương $OA^2=OG.OD$ . tức là $(O)$ trực giao với $(DLJ)$

Ngịch đảo tâm A phương tích bất kì , ta biến thành bài toán sau : Cho tam giác $ABC$. $E,F$ bất kì trên $AC,AB$ . $(AEF),(ABC)$ cắt nhau tại $D$. $J$ là trực tâm tam giác $AEF$ .$AJ$ cắt $ABC$ tại $L$ . Chứng minh  : tâm $(DJL)$ thuộc $BC$

Giải : $EF$ cắt $BC$ tại $P$

 Lấy $G$ đối xứng với $L$ qua $BC$ . dễ thấy $\Delta  GBC \sim  \Delta JFE$

Vị tự tâm $D$ tỉ số $DF/DB$ và xoay góc $(DB,DF)$ biến $B,C  \mapsto F,E$ . nên  $G  \mapsto J$ từ đó

 $ \widehat{GLJ}=\widehat{GLC}-\widehat{JLC}=\widehat{AFE}-\widehat{ABC}=\widehat{BPF}=\widehat{FDB}=\widehat{JDG} $ ($D$ là đ miquel )

nên $(DGJL)$ nội tiếp . có tâm thuộc trung trực $GL$ tức $BC$ , ta có dpcm

Lời giải bài 1:

Đầu tiên ta có 1 phát biểu (!) : Cho $O(ABCD)=-1$ .  $OA\perp O'A', OB\perp O'B', OC\perp O'C', OD\perp O'D'$ thì $O'(A'B'C'D')=-1$

 GỌi $(K)$ cắt $AB,AC$ tại $R,S$ . $(ARS)$ cắt $(O)$ tại $G,A$ 

Ta có $AG,EF$ , tiếp tuyến tại $D$ đồng quy tại $Y$ do là TDP của các cặp 3 đường tròn $(O),(K),(ARS)$

 Nếu $AD$ cắt $(K)$ tại $X$ thì $XRDS$ là tứ giác điều ghòa , và  tiếp tuyến tại $X,D$ và $AG,EF$ đồng quy nên $A(GDRS)=-1$

 vậy nên  theo (!)  $O(EFJM)=-1$ . điều đó chứng tỏ $O$ là trung điểm $MN$ 

Ta có $K(MNOY)=-1$ vậy nên theo (!) : $D(PQXY)=-1$ . khi đó $PQDX$ điều hòa , nên $PQ$ đi qua $Y$

Từ đó ta lại có $A(PQXY)=-1$ . Gọi  $MU$ cắt $NV$ tại $T$ . $Z$ sao cho $TZ$ vuông $AD$ .  Dựng $O'$ sao cho $TO'$ vuông $AG$ . Vậy theo (!)  thì $T(ZO'MN)=-1$ nên $TO'$ đi qua $O$ . mà $TO$ vuông $AG$ nên $TO$ đi qua $J$

Tóm lại ta có $T(UVZO)=-1,O(UVMT)=-1$ và $TZ$ song song  $MO$ nên $UV$ song song $OM$ , tức vuông góc với $AD$

Bài toán 196. Cho tam giác $ABC$ ngoại tiếp $(I)$ có tiếp điểm với $BC$ là $D$ , đường cao $BE,CF$ cắt nhau tại $H$.  Đường tròn nội tiếp tam giác $AEF$ cắt $EF,FA,AE$ tại $P,R,Q$ . Lấy $K$ sao cho $IK \perp IA$ và $DK=DI$ . $HK$ cắt $AI,RQ$ tại $J,L$ . Lấy $G$ đối xứng với $J$ qua $PL$ . $QR$ cắt $EF$ và đường thẳng qua $J$ song song với $EF$ tại $S,T$. $X,Y$ là trung điểm của $AS,JT$.Chứng minh rằng $LG \perp XY$ 

Lời giải bài 2

Gọi $Y$ là giao 2 tiếp tuyến tại $B,C$. $Z$ là trung điểm $OY$ . $J$ đối xứng với $O$ qua $BC$ . $N,M$ là trung điểm cung $BC,BC$

Ta có : $ON^2=OM.OY=OJ.OZ$ , suy ra $AZ,AJ$ đối xứng nhau quá phân giác góc $A$

Ta sẽ chứng minh $AX$ đi qua $Z$ cố định

Nghịch đảo $N$ tâm $A$ , phương tích $AB.AC$ hợp đối xứng trục phân giác góc $A$

Biến $H,B,C,O,BC \mapsto P,C,B,T,(O)$ . Trong đó $T$ đối xứng với $A$ qua $BC$

Gọi $BT,CP$ cắt $OC,BH$ tại $K,L$  mà $\widehat{OCA}=\widehat{BTA},\widehat{ABH}=\widehat{OPC}$ nên $KACT,ALPB$ vội tiếp

Từ đó $\widehat{KAC}=180-\widehat{BTC}=180-(180-BPC-\widehat{BAC})=180-LAC$

Suy ra $K,A,L$ thẳng hàng 

Áp dụng định lí Dersagues cho 2 tam giác $BHT,CPO$ , khi đó $TO,HP,BC$ đồng quy tại $X'$

Theo tales thì $AX'$ đi qua $J$

Chính vì vậy phép nghịch đảo $N$ :$X' \mapsto X$

Vậy $AX,AJ$ đẳng giác  , nên $AX$ đi qua $Z$ cố định do $AZ,AJ$ đối xứng nhau quá phân giác góc $A$

Cho tam giác ABC đường cao AH.I,J theo thứ tự là tâm bàng tiếp góc B,C của các tam giác ABH,ACH. Gọi P là tiếp điểm của BC với đường tròn nội tiếp tam giác ABC. Chứng minh bốn điểm I,J,P,H đồng viên.

Lời giải :

DO các phân giác ngoài , dễ thấy $\widehat{JHI}=90^o$

Ta cần cm  $\widehat{JDI}=90^o$ , Gọi $(I),(J)$ cắt $BC$ tại $E,F$

Ta có $ED=\frac{AB+BC-AC}{2}-BH+JE=\frac{AB+BC-AC}{2}-BH+\frac{AH+AC-HC}{2}=\frac{AH+AB-HC}{2}=IF$

CMTT ta có $FD=JE$ , suy ra 2 tam giác $JED,DFI$ bằng nhau , từ đó có $\widehat{JDI}=90^o$ nên $DHIJ$ nột tiếp

Lời giải bài 1 :

Gọi $(K)$ tiếp xúc với $(O)$ tại $Y$ . $I$ là tâm nội tam giác $ABC$.

Gọi $G$ là trung điểm cung $BC$ , $AG$ cắt $BC$ tại $T$ , ta có $M(GNAH)=-1$  nên  gọi $Q'$ là giao của $MN$ với $AG$ thì $(Q'GAT)=-1$. ta chứng minh $Q'$ trùng $Q$ , từ đó $AQ$ đy qua $G$ cố định

Thật vậy , tức là ta cần cm $X(PGAT)=-1$ với $X$ là giao của $PJ$ và $BC$

Gọi tiếp tuyến tại $P,Y$ cắt nhau tại $V$ thì xét trục đẳng phương $(K),(O),(PBC)$ thì $V$ thuộc $BC$ 

Suy ra $\frac{YB}{YC}=\sqrt{\frac{VB}{VC}}=\frac{PB}{PC}$ nên phân giác góc $BPC,BYC$ cắt nhau trên $BC$

Mặt khác , theo bài toán protassov thì $PJ$ là phân giác góc $BPC$ , từ đó suy ra $XY$ là phân giác góc $BYC$ 

Gọi $PL$ là phân giác ngoài $BPC$ suy ra $(LXBC)=-1$

$(K)$ cắt $AB,AC$ tại $E,F$ , $YE,YF$ cắt $(O)$ tại $Z,S$

ta so $ZS$ song song $EF$ nên $\frac{ZE}{ZY}=\frac{SY}{SY}=>\frac{ZE}{ZB}.\frac{ZB}{ZY}=\frac{SY}{SC}.\frac{SC}{SY}=>\frac{BE}{FC}=\frac{BY}{YC}=\frac{XB}{XC}$ suy ra $EF$ đy qua $L$ theo menelaus

Ta có $L$ đối cực với $XA$ qua $(K)$ nên $KL$ vuông góc với $XA$ tại $W$ , mặt khác $KP,KY$ là tiếp tuyến của $(XL)$

Chính vì vậy tứ giác $WPLY$ là tứ giác điều hòa  nên $X(WLPY)=-1=>X(PGAT)=-1$ , khi đó $XP$ đy qua $Q'$ , nên $Q$ trùng $Q'$ có dpcm

Lời giải bài 1 :

. Đối trung $AG$của tam giác $ABC$.$MA$ cắt $BL$ tại $A'$ .  $BM$ cắt $CN$ tại $P'$

Ta sẽ chứng minh $AP' \perp  BC$  .Ta có $\widehat{NAB}=\widehat{MAC}$ .và $NBA=MCA=90$  Dựng $U$ nằm ngoài tam giác và $AU \perp BC$ sao cho $\frac{AU}{BC}=\frac{AB}{BN}=\frac{AC}{CM}=>\bigtriangleup NBC\sim \bigtriangleup BAU,\bigtriangleup MBC\sim \bigtriangleup CUA$ Từ đó $BU\perp CN ,CU\perp BM$ nên $P'$ là trực tâm tam giác $UBC$ . Khi đó $AP' \perp BC$.

Gọi $LM$ cắt $AP'$ tại $P_1$.Do $L$ là trung điểm của $A'B$ nên $P_1$ là trung điểm $AP'$. trương tự suy ra $P'=P_1$ và là trung điểm $AP'$

$V_{A}^{2} :K,L,X,Y,Z,P \mapsto  K',L',X',Y',Z',T',P'$ Khi đó $P'$ là giao của $BM,CN$ ta chứng minh $(X'Y'Z')$ tiếp xúc $BC$

Ta sẽ chứng minh $AP' \perp  BC$  .Ta có $\widehat{NAB}=\widehat{MAC}$ .  Dựng $U$ nằm ngoài tam giác và $AU \perp BC$ sao cho $\frac{AU}{BC}=\frac{AB}{BN}=\frac{AC}{CM}=>\bigtriangleup NBC\sim \bigtriangleup BAU,\bigtriangleup MBC\sim \bigtriangleup CUA$ Từ đó $BU\perp CN ,CU\perp BM$ nên $P'$ là trực tâm tam giác $UBC$ . Khi đó $AP' \perp BC$

Tiếp theo ta có : $(AX'Z'BL')(AX'Y'CK')$ tiếp xúc với $BC$,.Mặt khác , Gọi tiếp tuyến tại $A$ của $(O)$ cắt $BC$ tại $T$ . Khi đó : $MN$ đy qua $T$ . $AO$ cắt $(O)$ tại $J$ .Khi đó , do $(TGBC)=-1$ nên $J,G,P'$ thẳng hàng

Nghịch đảo tâm $A$ phương tích bất kì : ( tên điểm vẫn giữ nguyên khi nghịch đảo )

Cho tam giác $AB$  nội tiếp $(Q)$ có đường cao $AJ$ . tiếp tuyến tại $B,C$ của $(ABC)$ cắt nhau tại $X'$. trung tuyến đỉnh $A$ cắt $(ABC)$ tại $G$. $(AGJ)$ cắt $AQ$ tại $P'$ . Đường thẳng qua $P'$ vuông góc với $AQ$ cắt $BX',CX'$ tại $Z',Y'$ . Chứng minh :$(X'Z'Y')$ tiếp xúc $(Q)$

Giải : ,

Gọi đường kính $AE$ . $GE$ cắt $BC$ tại $F$ . $R$ là trung điểm $BC$.  

Giả sử : $(BRG)(CRG)$ cắt $BX',CX'$ tại $Z_1,Y_1$ khi đó $\frac{RZ_1}{RY_1}=\frac{GZ_1}{GR}=\frac{GB}{GC}=\frac{AC}{AB}$

Suy ra $\bigtriangleup ABC \sim \bigtriangleup RY_1Z_1 \Rightarrow \widehat{RY_1Z_1}=\widehat{RY_1C}$ nên $R$ là tâm bàng tam giác $X'Y_1Z_1$ . Suy ra $(Q)$ là đường tròn $Mixtilinear$ của tam giác $X'Y_1Z_1$ nên $(X'Y_1Z_1)$ tiếp xúc $(Q)$

Ta cần chứng minh $Y_1,Z_1\equiv Y',Z'$ . Gọi $I$ là trung điểm cung $Y_1Z_1$ của $(X'Y_1Z_1)$  , khi đó Ta có các tc sau của dường tròn $Mixtilinear$ được cm ở đây ( https://nguyenvanlin...mixtilinear.pdf )

1) $IG\perp GR$

2) $IG,BC,Y_1Z_1$ đồng quy

 Khi đó $Y_1Z_1$ đy qua $P'$ và $Y_1Z_1$ vuông góc $AQ$( cộng góc ) nên $Y_1,Z_1\equiv Y',Z'$ . Ta có dpcm

Lời giải bài 2 :

Đầu tiên Ta có $\widehat{BFP}=\widehat{CEP}=\widehat{BAC}$ nên $FOPB,EOPC$ nội tiếp , Gọi $K,L$ là tâm $(OPB),(OPC)$ , Ta có $(K)=(L)$ . Dựng $X$ sao cho $X$ thuộc $PO$ và $\widehat{XKO}=\widehat{BAC}$ Nên $X$ cố định.  Mặt khác $\widehat{FPE}= \widehat{BAC}$ nên ta có :$\widehat{FKX}=\widehat{ELX}$ Do đó2 tam giác $FKX,ELX$ bằng nhau nên $XE=XF$ suy ra trung trực $FE$ đy qua $X$ cố định