ecchi123

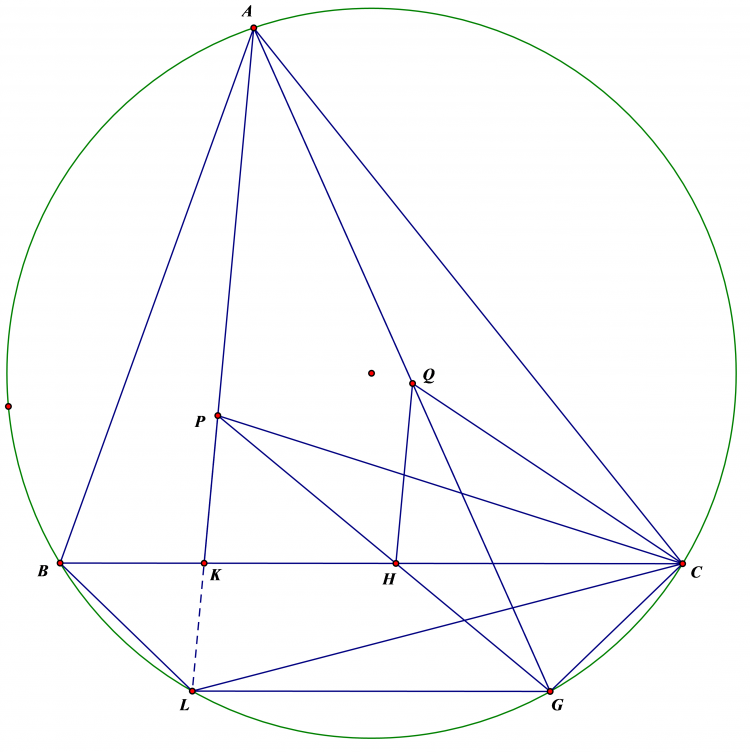
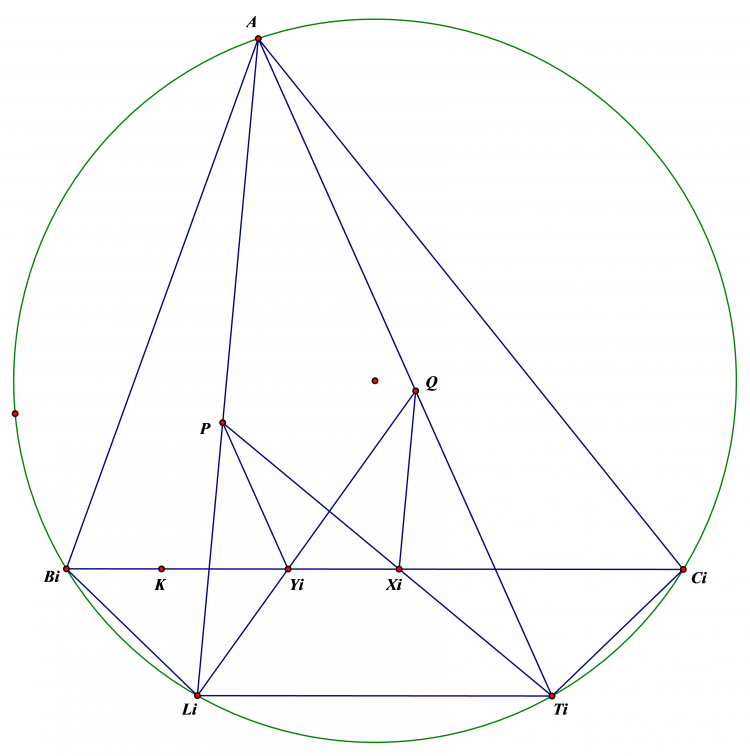
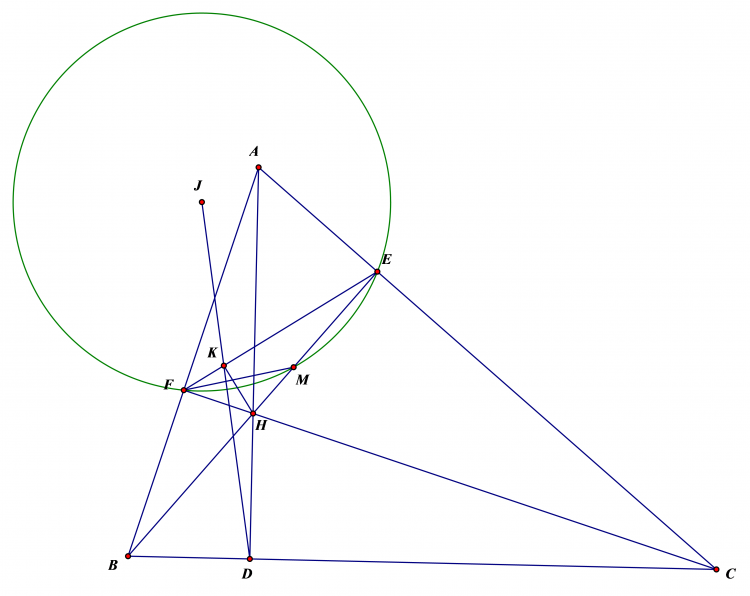
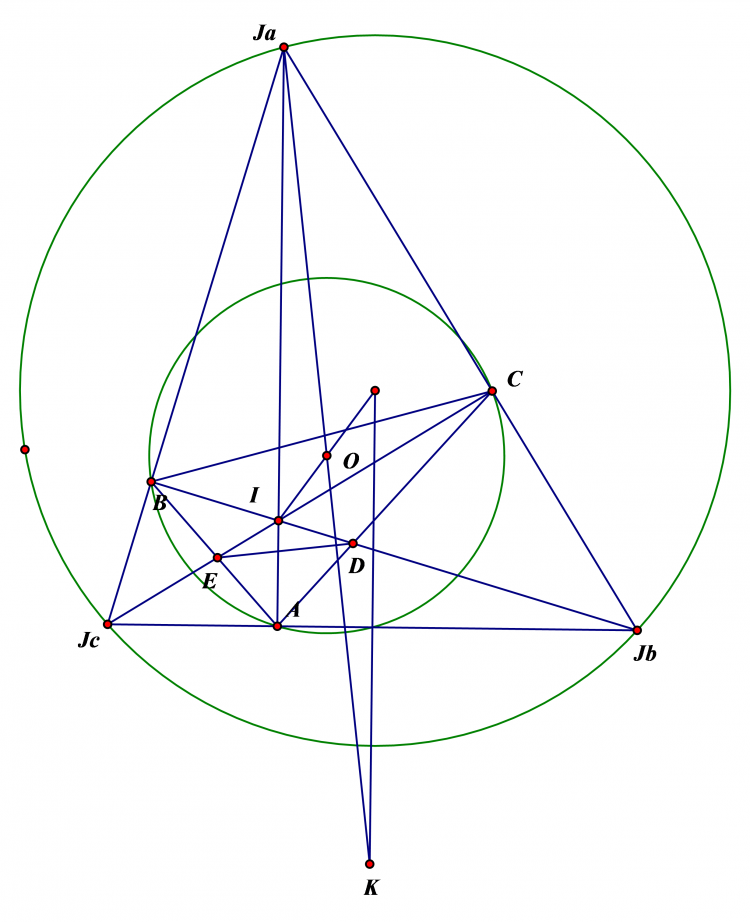
Cho tam giác ABC nội tiếp $\left ( O \right )$. Ba đường cao AD,BE,CF. EF cắt BC ở S. từ S kẻ tiếp tuyến SK tới $\left ( O \right )$. 

a,CMR KA là phân giác của góc EKF 

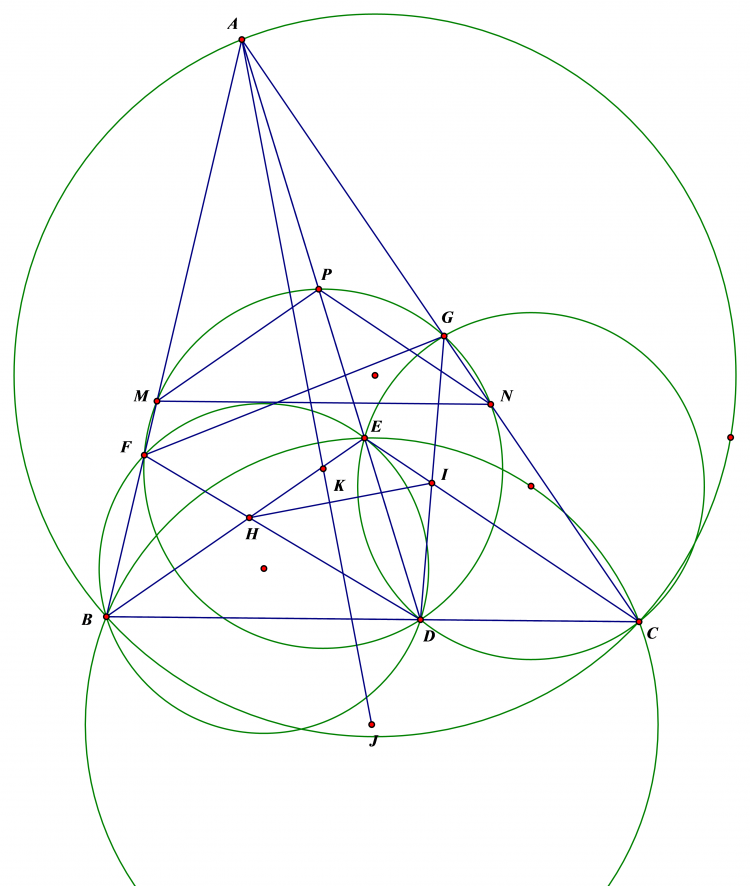
b,Gọi KD cắt EF ở L. Gọi I là trung điểm BC. AO cắt EF tại M. CMR IL $\perp$ AS và tứ giác BLMC nội tiếp

VMF_(1).png

a)$K$ của cả 2 trường hợp đều đúng , Mình sẽ chứng minh 1 th , th còn lại làm tương tự :

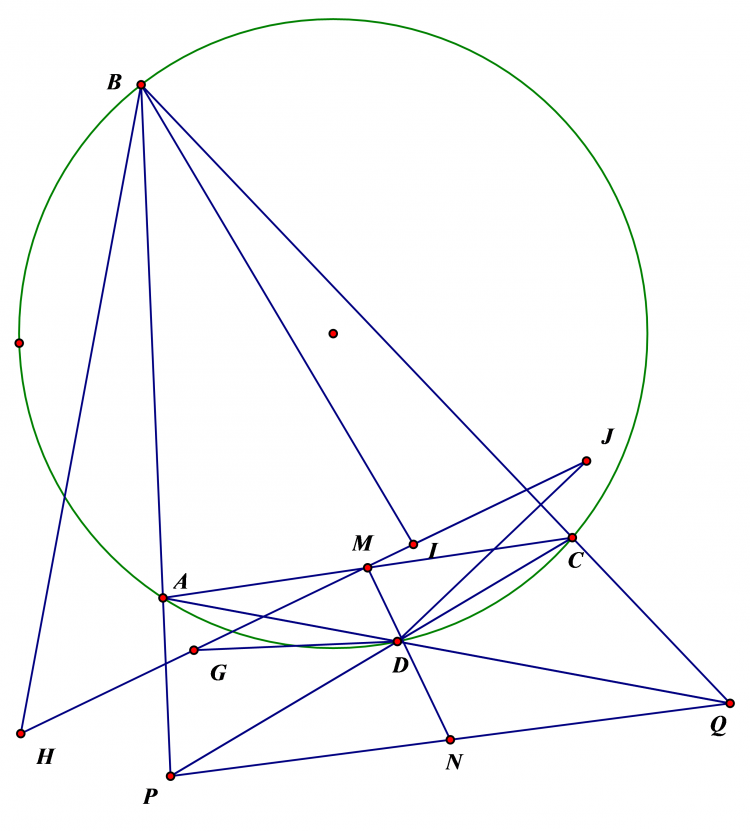
$K$ cùng phía với $A$ so với $BC$, có $KS^2=SB.SC=SE.SF$ nên $(KEF)$ ts $SK$ . 

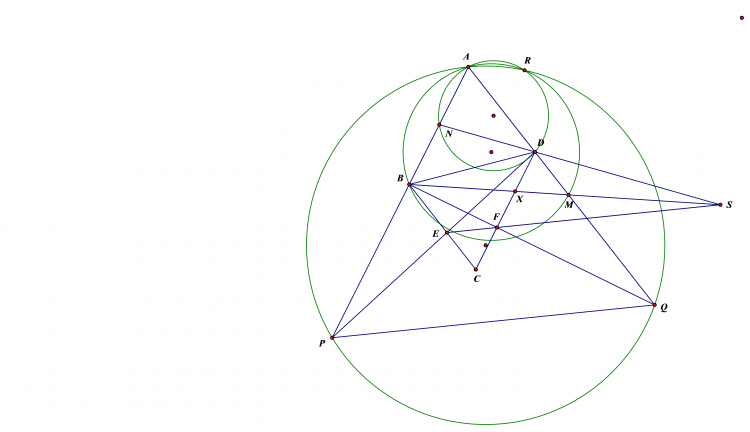
Gọi $KF$ cắt $(O)$ tại $Q$ , $CQ$ cắt $FE$ tại $P$ , ta có $\widehat{KCQ}=\widehat{SKQ}=\widehat{KES}$ nên $KECP$ nội tiếp

nên $\widehat{PKC}=\widehat{PEC}=180-\widehat{ABC}=180-\widehat{AKC}$ nên $P,K,A$ thẳng hàng  suy ra $\widehat{PKQ}=\widehat{ACQ}=\widehat{AKE}$ suy ra , $AK$ là phân giác ngoài góc $FKE$

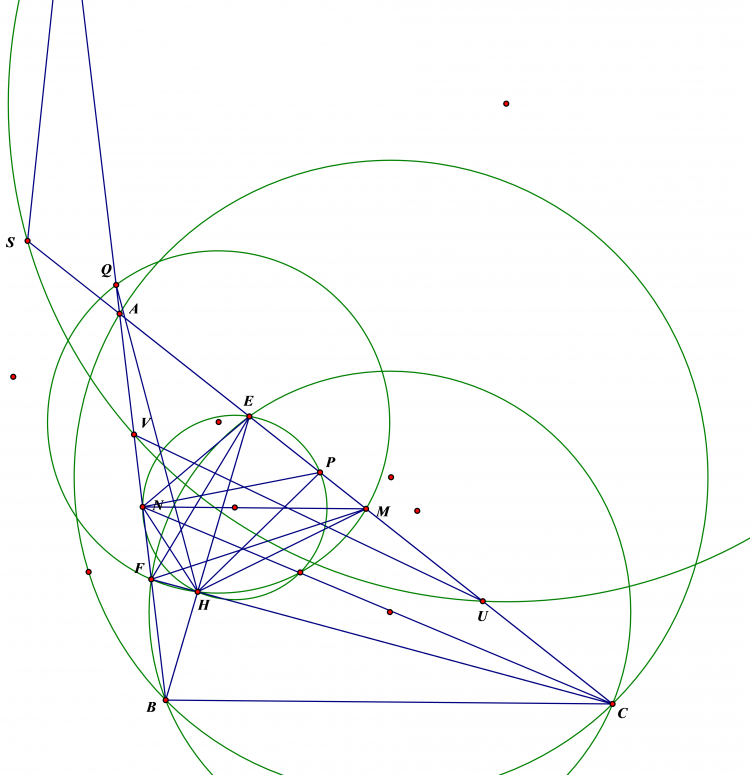
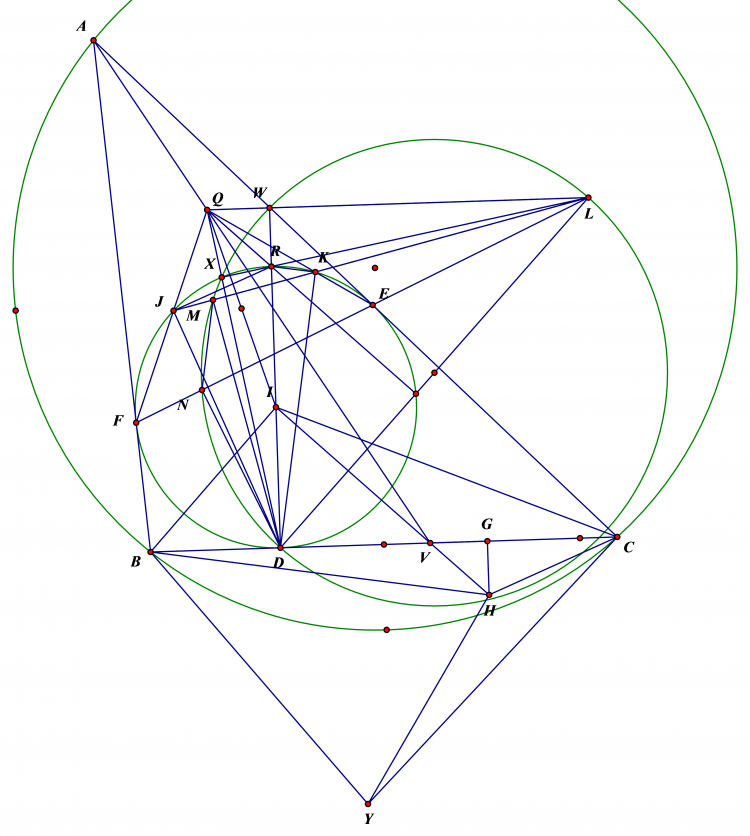
b) Dễ thấy $AM$ vuông góc $FE$ , $AM$ cắt $(O)$ tại $R$ .  GGoij $RH$ cắt $FE$ tại $L'$ . do r $HR$ vuông $Á$ nên ta chỉ cần cm $L$ trùng $L'$

ta có $AM.AR=AD.AH$ nên $DHNR$ nội tiếp suy ra

$\widehat{MDI}=90-\widehat{ADM}=90-\widehat{MRL'}$ nên $L'DIM$ nội tiếp , 

Có $\widehat{MSO}=\widehat{MIO}=90=\widehat{MID}=90-\widehat{SL'D}$ nên $SO$ vuông góc $LD$ , Mà $S$ liên hợp với $D$ qua $(O)$ nên $L'D$ là đường đối cực của $S$ qua $(O)$ nên $L',D,K$ thẳng hàng nên $L$ trùng $L'$ đồng thòi có $LDIM$ nội tiếp , 

( vì bạn sửa lại đề bài nên ko tiện tay sửa lại phần a , th hình như bạn thì làm tương tự cách làm trên , giống hệt luôn )

Lời giải bài 2 :  Trước khi giải , ta có 2 bài toán sau :

 

 

 BT1:  Cho tam giác $ABC$ nt $(O)$ , $P,Q$ là 2 điểm liên hợp đẳng giác trong tam giác , $AQ$ cắt $(O)$ tại $G$ . $GP$ cắt $BC$ tại $H$ . Chứng minh : $HQ$ song song $AG$ .

 

Lời giải : Gọi $AP$ cắt $BC, (O)$ tại $K,L$ . $\widehat{KPC}=\widehat{PAC}+\widehat{ACP}=\widehat{QCB}+\widehat{BCG}=\widehat{QCG}$

 

Nên ta có 2 tam giác $PLC,CGQ$ đồng dạng với nhau $\rightarrow LP.QG=CL.CG$ , 

 

Mặt khác 2 tam giác $LKC,GCA$ đồng dạng với nhau  $\rightarrow LK.AG=CL.CG$

 

Chính vì vậy $\frac{AG}{QG}=\frac{LP}{LK}=\frac{GP}{GH}$ nên $HQ$ song song $AG$

 

BT2: Cho Hình bình hành $ABCD$ cố định và 1 điểm $S$ cố định nằm bất kì . 1 đường thẳng $d$ thay đổi qua $S$ cắt $BC,CD$ tại $E,F$ . $DE,BF$ cắt $AB,AD$ tại $P,Q$ . Chứng minh : $(APQ)$ Luôn đi qua 2 điểm cố định khi $d$ thay đổi qua $S$

 

Lời giải : Goại $SD,SB$ cắt $AB,AD$ tại $N,M$ . $R$ là giao của $(AND)$ và $(ABM)$ khác $A$ . Có $R$ cố định . Ta sẽ chứng minh $(APQ)$ đi quá $R$. Gọi $CD$ cắt $BS$ tại $X$

 

 Áp dụng $Menelaus$ với tam giác $ADN$ cát tuyến $SBM$ Có: $\frac{BN}{BA}.\frac{MA}{MD}=\frac{SN}{SD}=\frac{SB}{SX}$

 

Tiếp tục  Áp dụng $Menelaus$ với tam giác $BCX$ cát tuyến $SEF$ Có :$\frac{SB}{SX}=\frac{EB}{EC}.\frac{FC}{FX}=\frac{PB}{AB}.\frac{FC}{FX}$

 

Mặt khác theo $Tales$ Có :$\frac{AM}{MQ}=\frac{AM}{AD}.\frac{AD}{AQ}.\frac{QA}{MQ}=\frac{CD}{CX}.\frac{CF}{CD}.\frac{AQ}{DQ-DM}=\frac{CD}{CX}.\frac{CF}{CD}.\frac{CX}{DF-DX}=\frac{CF}{FX}$

 

Từ 3 điều trên suy ra :$\frac{BN}{BP}=\frac{DM}{MQ}$ . Mặt khác có 2 tam giác $RBN,RDM$ đồng dạng với nhau và có tỉ số trên suy ra 2 tam giác $RBP,RMQ$ đòng dạng nên $\widehat{RPA}=\widehat{RQA}$ Suy ra $APQR$ nội tiếp (dpcm)

 

Trở lại bài toán đầu : 

 

Bài toán đưa về các đường tròn ngoại tiếp tam giác $AB_iC_i$ thỏa mãn 2 tính chất trên đy qua 1 điểm cố đinh khác $A$ . 

 

Gọi  $AP,AQ$ cắt $(AB_iC_i)$ tại $L_i,T_i$ . $PT_i,QL_i$ cắt $B_i,C_i$ tại $X_i,Y_i$ thì theo BT1  thì $PY_i,QX_i$ song song với $AQ,AP$ .

 

Do $B_i,C_i$ thay đổi theo 2 điều kiện Và với mỗi $Y_i,X_i$ có đặc điểm như trên  thì ta dựng được duy nhất $(AB_iC_i)$ theo cách như trên ( hình vẽ )

 

. Chính vì vậy , ĐỀ bài sẽ đưa về chứng minh $(AL_iT_i)$ đy qua điểm cố định , Đây chính là BT2

 

Ta có dpcm,

Lời giải Bài 1 :

Dễ thấy $AT=2NQ,AS=2PM$ và $\widehat{NHP}=\widehat{AEN}=\widehat{AFM}=\widehat{QHM}=>\widehat{NHQ}=\widehat{MHP}$

Và ta cũng có 2 tam giác $AFC,AEB$ đồng dạng với nhau nên $\widehat{NEB}=\widehat{MFC}$

Ta có hàng loạt các biến đổi sau để có dpcm:

$\frac{AT}{AS}=\frac{NQ}{MP}=\frac{NQ}{Sin\widehat{NHQ}}.\frac{Sin\widehat{MHP}}{MP}=\frac{HN}{Sin\widehat{NQH}}.\frac{Sin\widehat{MPH}}{HM}=\frac{NH.Sin\widehat{ENH}}{MH.Sin\widehat{FMH}}=\frac{EH.Sin\widehat{NEB}}{FH.Sin\widehat{MFC}}=\frac{EH}{FH}=\frac{CE}{BF}=\frac{AU}{AV}$

Suy ra $STUV$ nội tiếp

Bài toán 186: Cho tam giác $ABC, $đường cao $AD,BE,CF$ đồng quy tại $H.HK$ vuông góc với $EF.M$ thuộc $BE$ sao cho $KM$ song song với $BC.J$ là tâm $(MEF).$ Chứng minh $J \in DK.$

Lời giải bài 185 :  

 

Ta sẽ chứng minh  $K$ thuộc đường thẳng qua $B$ vuông góc với $OO'$

 

 

Để dễ nhìn, ta viết lại đề như sau : Cho tam giác $ABC$ ngoại tiếp $(I),(I)$ tiếp xúc với $BC,CA,AB$ tại $D,E,F.G$ đối xứng với $D$ qua trung điểm $BC.H$ bất kì sao cho $GH$ vuông góc $BC.$ Đường thẳng qua $D$  vuông góc với $HB,HC$ cắt $(I)$ tại $K,J.JK$ cắt $FE$ tại $L.$ Chứng minh $DL$ vuông góc với $IH.$

 

 

Giải : Hạ $DM,DN$ vuông góc với $JK,EF$ , Ta có : $\frac{JM}{KM}=\frac{JM}{MD}.\frac{MD}{MK}=\frac{GH}{BG}.\frac{CG}{HG}=\frac{BG}{CG}=\frac{CD}{BD}=\frac{EN}{FN}$

 

Gọi $FJ$ cắt $KE$ tại $Q,W$ là điểm $Miquel$ của tứ giác toàn phần $JKEF.LQ$ thì theo tỉ số trên có $(LJF),(LMN),(LEK)$ đồng trục $LW.$

Gọi $DQ$ cắt $(I)$ tại $X,R$ đối xứng với $D$ qua $I.$ Do $\overline{QW}.\overline{QL}=\overline{QJ}.\overline{QF}$ nên $Q$ thuộc trục đẳng phương của $(DMNL)$ nên $X$ thuộc $(MNDL),$ mà $DW$ và $IW$ cùng vuông góc với $QL$ (do $QX.QD=QW.QL$ và góc $DXL$ vuông) nên $DR$ vuông góc với $QL \Rightarrow R$ là trực tâm tam giác $QDL$ nên $QR$ vuông góc với $DL.$

 

Bây giờ ta sẽ chứng minh $QR$ song song $HI.$ Dựng $Y$ nằm ngoài tam giác $ABC$ sao cho$\widehat{HBY}=\widehat{\frac{B}{2}},\widehat{HCY}=\widehat{\frac{C}{2}}.$

Ta có tam giác $RJK$ đồng dạng với $HBC$ và theo cách dựng $Y$ ta cũng có được tam giác $QJK$ đồng dạng $YBC.$

Mặt khác , xét tam giác $BCH$ có $BY,BI$ đẳng giác góc $B;CY,CI$ đẳng giác góc $C$ nên $Y,I$ liên hợp đẳng giác tam giác $HBC$ nên $HI,HY$ đẳng giác góc $H.$

Chính vì vậy $\widehat{QRK}=\widehat{YHC}=180^0-\widehat{BHI}$ và  $BH,RK$ song song với nhau nên $QR,HI$ song song với nhau.

Kết hợp với $QR$ vuông góc với $DL$ suy ra $DL$ vuông góc với $IH,$ đpcm.

 

Bài toán 184. Cho tam giác $ABC$ , $M$ nằm trên đoạn $BC$ , $K,L$ là tâm ngoại tiếp $(ABM),(ACM).D,E,F,X,Y,Z,T$ lần lượt là trung điểm $MA,MB,MC,KB,KM,LM,LC.YZ$ cắt $XT$ tại $N.NL,NK$ cắt $BC$ tại $P,Q.$ Chứng minh $(DPF)$ tiếp xúc $(DEQ).$

Bài toán 182. Cho tam giác $ABC$ nhọn, nội tiếp $(O)$ và ngoại tiếp $(I).P$ là điểm bất kì trên cung nhỏ $BC.$

$M,N$ là hai điểm nằm trên cạnh $BC$ sao cho tam giác $MNP$ nhận $(I)$ làm đường tròn bàng tiếp góc $P$ và $(MNP)$ cắt lại $(O)$ ở $X.$

Chứng minh $AX$ đi qua tâm vị tự của $(O),(I).$

Lời giải bài 182 : Đầu tiên ta đi chứng minh $X$ là tiếp điểm của $A-Mix$ với $(O)$

Thật vậy : Gọi $PM,PN$ cắt $(O)$ tại $F,E$ , $EF$ cắt $BC$ tại $Q$ Khi đó $Q$ là điểm $Miquel$ của tứ giác toàn phần $EFMN.PQ$

Ngịch đảo  tâm $X$ phương tích $XM.XE$ hợp đối xứng phân giác góc $MXE$ do $EFMN$ ngoại tiếp nên $XI$ là phân giác góc $QXP$ , (  https://nguyenvanlin...ao-doi-xung.pdf )

có$\widehat{QXB}=\widehat{XBC}-\widehat{XQC}=\widehat{XBC}-\widehat{XFP}=\widehat{PXC}$ nên $XI$ cũng là phân giác góc $CXB$ nên $X$ là tiếp điểm của $A-Mix$ với $(O)$

Xét các tâm vị tự ngoài của $(O),(I),(A-Mix)$ thì theo định lý $Monge$ thì $AX$ đi qua tâm vị tự của $(O),(I).$

Bài toán 180. Cho ngũ giác $ABCDE$ lồi, điểm $F$ trên cạnh $AE$ thỏa mãn $\Delta ABC \sim \Delta CDE \sim \Delta BFD.$ Chứng minh $\frac{AF}{FE}=\frac{BF^2}{FD^2}.$

Lời giải bài toán 180. Gọi $DF$ cắt $AC$ tại $G,BF$ cắt $CD$ tại $H,$ có $BCDG,BCDH$ nội tiếp nên $G,B,C,D,H$ cùng thuộc 1 đường tròn.

Theo định lý Pascal thì $BA$ cắt $DE$ tại $I$ thuộc $(GBCDH).$

Do đó $\frac{AF}{FE}=\frac{AB.\sin \widehat{ABF}}{HE.\sin\widehat{FHE}}=\frac{AB.HI}{HE.BC}=\frac{BF^2}{DF^2},$ đpcm.

 

Bài toán 178. Cho tam giác $ABC$ nội tiếp $(O)$ có trực tâm $H,$ phân giác $AD.M$ là điểm chính giữa cung $BHC$ của $(BHC).BM,CM$ cắt $AC,AB$ tại $E,F.EF,AM$ cắt nhau tại $P.K$ là tâm $(AEF).$ Chứng minh :$P$ là trực tâm tam giác $KBC$ và $KA=OD.$ 

Lời giải bài toán 177.

Bổ đề. Cho tam giác $ABC$ , $D,E$ nằm trên $AB,AC$ , $K,H$ là trực tâm tam giác $ABC,ADE$ , $M,N,P,Q,F$ là trung điểm $BC,CE,DE,BC,DC.$ Khi đó tam giác $AHK$ đồng dạng tam giác $FNM.$

Chứng minh. Gọi $J,I$ là tâm ngoại $ABC,ADE$ , ta có $\frac{AH}{AK}=\frac{IP}{JQ}=\frac{DE}{BC}=\frac{FN}{FM}$

Và dễ dàng chứng minh :$\widehat{HAK}=\widehat{NFM}$ suy ra $AHK$ đồng dạng tam giác $FNM$

Từ đây còn suy ra $\frac{HK}{MN}=\frac{HA}{FN}=\frac{2PI}{PE}=2tan\widehat{DEI}=2cot\widehat{DAE}$

Trở lại bải toán :

Gọi $H,G,I,J$ là trực tâm tam giác $BAQ,PAD,PBC,CDQ$ , ta sẽ chứng minh $GJ=HI$

Thật vậy , gọi $M,N$ là trung điểm $AC,PQ$ , khi đó theo Bổ đề $\frac{GJ}{MN}=2 cot\widehat{ADP}$

 Mặt khác , ta cũng có $\frac{HI}{MN}=2cot\widehat{ABC}$ từ đó suy ra$GJ=HI$

Mình đã giải bài toán tổng quát của bổ đề này:

Cho tam giác $ABC$ nhọn. Lấy $D$ là 1 điểm bất kì trên đoạn $BC$ không trùng $B,C$. Lấy $E$ là 1 điểm trên đoạn $AD$ ($E$ không trùng $A,D$). Gọi $(DEB)$ cắt $AB$ tại $F$ khác $B$ và gọi $(DEC)$ cắt $AC$ tại $G$ khác $C$. $EC$ cắt $GD$ tại $I$ và $FD$ cắt $BE$ tại $H$. Gọi $J$ là tâm đường tròn ngoại tiếp tam giác $EBC$. Chứng minh rằng: $AJ$ vuông góc $HI$.

Cảm ơn bạn đã  có một bài toán tổng quát , Mình có 1 cách giải cho bài toán này

 ta có $\overline{HF}.\overline{HD}=\overline{HE}.\overline{HB}$ và tương tự với $I$ , ta được $HI$ là trục đẳng phương của $(BEC),(DFG)$ . $K$ là tâm $(DFG)$ thì $JK$ vuông góc $HI$

Gọi $(DFG)$ cắt $AB,AC,AD$ tại $M,N,P$ , dễ thấy $MN$ song song với $BC$ , $\widehat{PNA}=\widehat{ADG}=\widehat{ACE}$ suy ra $PN$ song song $EC$ , tương tự thì $PM$ song song $EB$ , suy ra có phép vị tự tâm $A$ biến tam giác $PMN$ thành $EBC$ nên $K,J,A$ thẳng hàng , Nên $AJ$ vuông góc với $IH$

Bài toán 176. Cho tam giác $ABC$ nội tiếp $(O),B,C$ cố định, $A$ di chuyển trên cung lớn $BC,$ phân giác $AD,K$ bất kì cố định trên trung trực $BC,$ đường thẳng qua $D$ vuông góc $BC$ cắt $AK$ tại $T.$ Chứng minh $(T,TD)$ luôn tiếp xúc với 1 đường tròn cố định khi $A$ thay đổi.

Lời giải bài toán 175.

Vị tự tâm $H$ tí số $1/2$ , Gọi $HE,HF$ vuông góc với $AM,AN$ , ta chứng minh $(DEF)$ tiếp xúc với $(Euler)$ của tam giác $ABC$

Trước tiên , $AH$ cắt $BC$ tại $K$ thì$\overline{AH}.\overline{AK}=\overline{AF}.\overline{AD}=\overline{AE}.\overline{AM}$ nên $(DEF)$ đy qua $M$

 Gọi tiếp tuyến tại $A$ cắt $BC$ tại $T$ , theo bài toán quen thuộc thì $E$ thuộc $(A-Apolo)$ Suy ra $TE=TA$ và $ED$ là đối trung của $EBC$ suy ra $ED,EM$ đẳng giác trong  góc $BEC$ nên $\widehat{DEM}=\widehat{BEC}-2\widehat{MEC}=\widehat{B}-\widehat{C}=180^0-\widehat{AOM}$

 Suy ra $\widehat{EDC}=\widehat{AMC}-\widehat{DEM}=90^0-\widehat{MAO}=90^0-\widehat{KAD}=\widehat{ADK}$

Chính vì vậy $ME=MF$ ta có , trung trực của $EF$  vừa đy qua tâm $(Euler)$ của tam giác $ABC$ vừa đy qua tâm $DFE$ và $M$ nên $(DEF)$ tiếp xúc với $(Euler)$ của tam giác $ABC$ tại $M.$

Bạn chứng minh bổ đề trên được không?

Mình xin trích lại bổ đề : , Cho tam giác $ABC$ nt $(O)$ phân giác $BD,CE$ cắt nhau tại $I$ , $J_a,J_b,J_c$ là các tâm bàng , Chứng minh : $OJ_a$ vuông góc với $DE$

Giải : Đàu tiên , có $(O)$ là $(Euler)$ của tam giá c$J_aJ_bJ_c$ 

Dễ thầy $J$ là trực tâm tam giác $J_aJ_bJ_c$ . Gọi $K$ là tâm $(J_{b}J_{c}I)$ Khi đó $O,J_a,K$ thẳng hàng

Xét trục đẳng phương của $(K),(O)$ có $\overline{EB}.\overline{EA}=\overline{EI}.\overline{EI_c}$ và $\overline{DC}.\overline{DA}=\overline{DI}.\overline{DI_b}$ nên $DE$ là trục đẳng phương của $(K),(O)$ khi đó $DE$ vuông góc với $\overline{J_aOK}$

Tam giác ABC nhọn, H trực tâm. Tiếp tuyến tại A với đường tròn ngoại tiếp tam giác ABC cắt BC tại P. Từ P kẻ tiếp tuyến PQ đến (HBC). H và Q nămf cùng phía trên mặt phẳng bờ BC.Chứng minh rằng góc HQA là góc vuông

Gọi $K$ là tâm $HBC$ , suy ra $\Delta PQK=\Delta PAO$ nên $\Delta PAQ$ đồng dạng $\Delta POK$ 

Ta có :$\widehat{HAQ}=\widehat{QAP}-\widehat{HAP}=\widehat{KOP}+90^0-(\widehat{C}-\widehat{B})=180^0-(\widehat{C}-\widehat{B})-\widehat{OPB}=\widehat{APO}$

Và $\frac{AQ}{AP}=\frac{OP}{OK}=\frac{OP}{AH}$

Tứ 2 điều trên suy ra $\Delta APO$ đồng dạng $\Delta QAH$ nên  $HAQ$ vuông tại $Q$