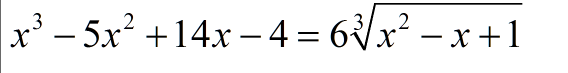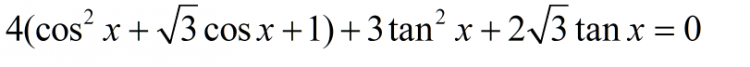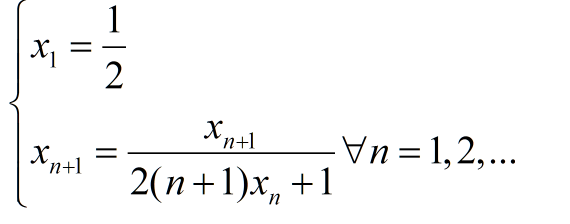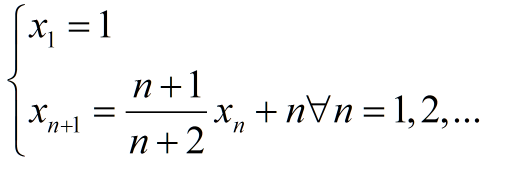Cho $(O,R)$, $(O',R')$, $(O'',R'')$ thỏa mãn $(O'), (O'')$ tiếp xúc ngoài tại $T$ và lần lượt tiếp xúc trong với đường tròn tâm $(O)$ tại $D,E$. Tiếp tuyến chung ngoài $FG$ của hai đường tròn $(O'), (O'')$ ($F$ trên $(O')$, $G$ trên $(O'')$) , $FG$ giao đường tròn tâm $O$ tại $A,B$. Tiếp tuyến tại T của $(O'), (O'')$ cắt $(O)$ ở $C$ ($C$ cùng phía $D$ so với $FG$).
Chứng minh rằng: $TA+TB+TC\leq \frac{\sqrt{3}}{2}(AB+BC+CA)$.
- kimchitwinkle yêu thích



 Tìm kiếm
Tìm kiếm Không khai báo
Không khai báo











 Gửi bởi
Gửi bởi