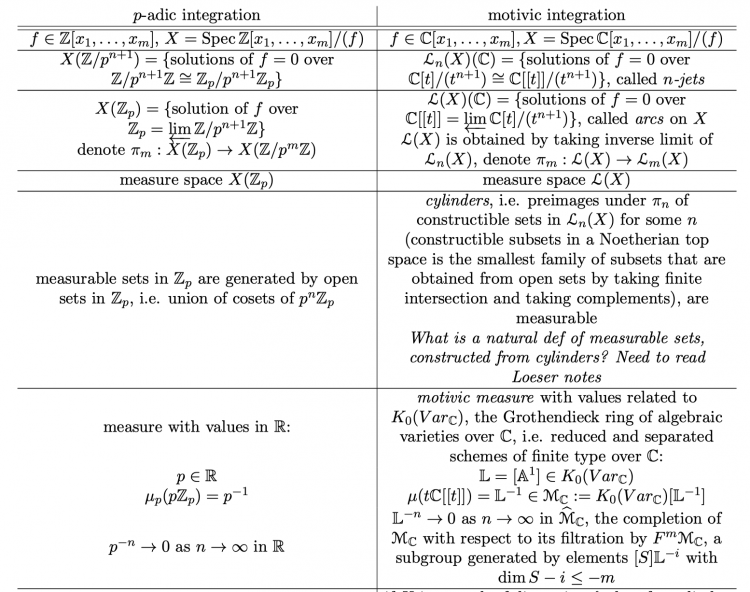
Hồi đầu năm cũng có học khoán về motivic integration, lúc đó có lập được một cái bảng so sánh với p-adic integration như thế này:
Link tham khảo:
- Mihnea Popa https://people.math..../571/index.html
- Francois Loeser Arizona winter school notes
- Devlin Mallory notes Motivic integration
- Willem Veys Arc spaces, motivic integration and stringy invariants.
Trong motivic integration, Bằng có biết có công thức change of variables tổng quát cho bất kì $\alpha: C\to \mathbb{Z}\cup \{\infty\}$ thay vì chỉ $\alpha: J_{\infty}(X)\to \mathbb{N}$ không nhỉ?
- DOTOANNANG yêu thích



 Tìm kiếm
Tìm kiếm Nam
Nam











 Gửi bởi
Gửi bởi