Chủ đề này có 12 trả lời

[thieutoan1B]

1- Cho A là ma trận vuông cấp n. Cmr $r(A^n) = r(A^{n+1})$.
2- Cho A, B là ma trận vuông cấp n thỏa AB = 0. Cmr có ít nhất một trong 2 ma trận
$A + A^{t}$, $B + B^{t}$ là suy biến.

Bài viết đã được chỉnh sửa nội dung bởi vo van duc: 07-10-2013 - 06:58

[toanA37]

Pro1: r(A) n. Mặt khác r(A) r(A^{2} ... r(A^{n}...). Đó là một dãy các số tự nhiên giảm dần. Do đó tồn tại một số K sao cho r(A) r(A^{2} ... r(A^{K}=r(A^{K+1}=...). Dễ thấy K n. Do đó r(A^{n}=r(A^{n+1})).
Pro2: Sử dụng các tính chất cơ bản về hạng của ma trận:
+ r(A+B) r(A)+r(B).
+ r(AB)+n r(A)+r(B).
+ r(A) = r(A^t)
Ta có thể chứng minh được bài toán trong trường hợp n lẻ. Còn với n chẵn thì liệu bài toán còn đúng không????

[nguyendangson]

Pro1: r(A) n. Mặt khác r(A) r(A^{2} ... r(A^{n}...). Đó là một dãy các số tự nhiên giảm dần. Do đó tồn tại một số K sao cho r(A) r(A^{2} ... r(A^{K}=r(A^{K+1}=...). Dễ thấy K n. Do đó r(A^{n}=r(A^{n+1})).
Pro2: Sử dụng các tính chất cơ bản về hạng của ma trận:
+ r(A+B) r(A)+r(B).
+ r(AB)+n r(A)+r(B).
+ r(A) = r(A^t)
Ta có thể chứng minh được bài toán trong trường hợp n lẻ. Còn với n chẵn thì liệu bài toán còn đúng không????

Cai de thay k<=n cua ban co the giai thich ro rang hon duoc khong.
Neu luc do voi k >n thi A^k +1=A^k +n thi sao.

[nhungtuyet]

1- Cho A là ma trận vuông cấp n. Cmr $ r(A^n) = r(A^{n+1}) $
2- Cho A, B là ma trận vuông cấp n thỏa AB = 0. Cmr có ít nhất một trong 2 ma trận
$A + A^{t}, B + B^t $ là suy biến.

Pro1: r(A) n. Mặt khác $r(A) \geq r(A^{2}) \geq ... \geq r(A^{n})...)$. Đó là một dãy các số tự nhiên giảm dần. Do đó tồn tại một số K sao cho $r(A) \geq r(A^{2}) \geq ... \geq r(A^{K})=r(A^{K+1})=... $.
Dễ thấy K 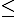n.
Do đó $ r(A^{n})=r(A^{n+1}) $
Pro2: Sử dụng các tính chất cơ bản về hạng của ma trận:
+ r(A+B) 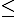r(A)+r(B).
+ r(AB)+n r(A)+r(B).
+ r(A) = $ r(A^t)$
Ta có thể chứng minh được bài toán trong trường hợp n lẻ. Còn với n chẵn thì liệu bài toán còn đúng không????

C/m: Tồn tại k để $ A^k \geq A^{k+1} $ và $ k \leq n$
Do $ r(A) \leq r(A^2) \leq...\leq r(A^n) \leq r(A^{n+1} \leq ... $
Đây là dãy số tự nhiên giảm dần ( đến số m nào đó thì $ r(A^m)=0 $)
Nếu mà trong dãy bất đẳng thức trên có dấu bằng thì dễ suy rồi.
Trường hợp xấu nhất là dãy bdt trên đều là dấu > từ r(A) ...đến $ r(A^n) $.
Khi ấy rõ ràng $ r(A^n) = $ 1 hoặc 0.
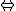
Nếu mà $r(A^n) =0 $ A=0 $ r(A^{n+1})=0 $
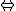
Nếu $r(A^n) =1 $ giả sử $ r(A^n)>r(A^{n+1}) $ thì $ r(A^{n+1})=0 $ $ A^{n+1}=0 $
Ta c/m được nếu $ A^m=0 $ thì $ A^n =0$
$ A^n =0 $ $ r(A^n)=0 $ (trái gt $ r(A^n)=1) $ vậy $ r(A^n)=r(A^{n+1}) $
Vậy luôn có $ r(A^n)=r(A^{n+1}) $

Bài viết đã được chỉnh sửa nội dung bởi nhungtuyet: 06-03-2010 - 20:10

[vuthanhtu_hd]

1- Cho A là ma trận vuông cấp n. Cmr r(A^n) = r(A^{n+1}).
2- Cho A, B là ma trận vuông cấp n thỏa AB = 0. Cmr có ít nhất một trong 2 ma trận
A + A^{t}, B + B^{t} là suy biến.

Bài 1 là đề thi OLP Toán,Đại số năm 1997

[nhungtuyet]

Đề năm 97 là thế này:
Chứng minh rằng với 1 ma trận vuông cấp n cho trước trên trường số thực, đều tìm được số nguyên n sao cho hạng
$ r(A^k)=r(A^{k+1}) \gamma k \geq n $
Anh vuthanhtu_hd học ĐH Công nghệ à!

Bài viết đã được chỉnh sửa nội dung bởi nhungtuyet: 06-03-2010 - 23:31

[vuthanhtu_hd]

Đề năm 97 là thế này:
Chứng minh rằng với 1 ma trận vuông cấp n cho trước trên trường số thực, đều tìm được số nguyên n sao cho hạng
$ r(A^k)=r(A^{k+1}) \gamma k \geq n $
Anh vuthanhtu_hd học ĐH Công nghệ à!

Mình mới năm thứ nhất thôi,chắc ít tuổi hơn bạn

[nhungtuyet]

Sao bạn đoán là ít tuổi hơn!
Nếu bạn không học trước lớp thì bằng tuổi rùi!

[HUS]

không ai viết bài 2 ah? bài này chỉ đúng cho trường hợp $n$ lẻ.
giả sử $A+A^T$ là ma trận khả nghịch, thế thì $n=rank(A+A^T) \leq rankA+rankA^T=2rankA$ =>$ rankA \geq \dfrac{n}{2}$ =>$rankA \geq \dfrac{n+1}{2}$. ta có $n=n+rankAB \geq rankA+rankB \geq \dfrac{n+1}{2}+rankB$ => $rankB \leq \dfrac{n-1}{2}$
và do đó $rank(B+B^T) \leq rankB+rankB^T=2rankB \leq n-1$ suy ra $B+B^T$ suy biến. ok

[okbabi]

Pro1: r(A) n. Mặt khác r(A) r(A^{2} ... r(A^{n}...). Đó là một dãy các số tự nhiên giảm dần. Do đó tồn tại một số K sao cho r(A) r(A^{2} ... r(A^{K}=r(A^{K+1}=...). Dễ thấy K n. Do đó r(A^{n}=r(A^{n+1})).
Pro2: Sử dụng các tính chất cơ bản về hạng của ma trận:
+ r(A+B) r(A)+r(B).
+ r(AB)+n r(A)+r(B).
+ r(A) = r(A^t)
Ta có thể chứng minh được bài toán trong trường hợp n lẻ. Còn với n chẵn thì liệu bài toán còn đúng không????

bài 2 chỉ chứng minh được khi n là số lẻ còn số chẳn k CM được !

[redline]

bài 2 chỉ chứng minh được khi n là số lẻ còn số chẳn k CM được !

Nói chung bài 2 sai khi $n$ là số chẵn. Ví dụ khi $n=2$ ta xét hai ma trận thực là

$A= \begin{bmatrix} -1 & 1\\ -1& 1 \end{bmatrix}$ và $B=\begin{bmatrix} 2 & 1\\ 2 & 1\end{bmatrix}$.

Bài viết đã được chỉnh sửa nội dung bởi redline: 24-03-2012 - 00:13

[redline]

bài 2 chỉ chứng minh được khi n là số lẻ còn số chẳn k CM được !

Trường hợp $n=2m$ là một số chẵn dương bất kỳ, ta xây dựng ma trận $A$ cấp $n$ sao cho $A^2=O$ và ma trận $A+A^t$ khả nghịch như sau: Gọi $E_m$ là ma trận đơn vị cấp $m$; $O_m$ là ma trận không cấp $m$. Khi đó $A$ xác định từ ma trận khối như sau:
$A= \begin{bmatrix} O_m & O_m \\ E_m & O_m \end{bmatrix}$
thỏa mã yêu cầu trên.

[okbabi]

ừa