Chủ đề này có 452 trả lời

[ninhxa]

______________________________
Bài 45: Cho $\triangle ABC$, $H$ là trực tâm.
CMR: $\frac{BH.CH}{AB.AC}+\frac{CH.AH}{BC.BA} + \frac{AH.BH}{AC.BC} =1$
p/s: bài không khó

-Ta có
$\Delta CHE\sim \Delta BAE(g-g)$
$\to \frac{CH}{AB}=\frac{CE}{BE}$
$\to \frac{CH.BH}{AB.AC}=\frac{CE.BH}{BE.AC}=\frac{S_{BHC}}{S_{ABC}}$
-Xây dựng các đẳng thức tương tự ta được dpcm/

Bài viết đã được chỉnh sửa nội dung bởi ninhxa: 24-07-2012 - 09:42

[Beautifulsunrise]

Bài 46: Cho tam giác $ABC$ có $3BC^2=2(AB^2+AC^2)$. $O$ là trung điểm $BC$. $H$ là trực tâm tam giác $ABC$. Chứng minh: $HA=HO$
___________________
Hàng tự chế chưa kiểm định chất lượng

Bổ đề 1 (Cosin):
$BC^2 = AB^2 + AC^2 - 2AB.ACcosA$

Bổ đề 2 (Công thức trung tuyến):
AM là trung tuyến của tam giác ABC:
$4AM^2 = 2AB^2 + 2AC^2 - BC^2$

Trở lại bài toán:

Bài viết đã được chỉnh sửa nội dung bởi binhmetric: 24-07-2012 - 12:18

[Beautifulsunrise]

Mấy bài này ở đâu thế chú.

Mấy bài đó ở một nơi mới đầu mình thấy xa lắm, nhưng giờ mình lại thấy chúng ở rất gần, ở ngay trước mặt mình luôn:
TOPIC VỀ CÁC BÀI HÌNH KHÓ THCS
Bắt đầu bởi henry0905, Jul 05 2012 19:13. Trang 9. @_^

Bài viết đã được chỉnh sửa nội dung bởi binhmetric: 24-07-2012 - 21:29

[Tru09]

Bài 47: Cho tam giác $ABC$ nội tiếp đường tròn $(O)$, gọi $M$ là trung điểm của $BC$. Trên đường thẳng $BC$ lấy hai điểm $I$, $J$ đối xứng với nhau qua $M$. Gọi $E$, $F$ lần lượt là giao điểm thứ hai của $AI$, $AJ$ với đường tròn $(O)$ và $H$ là trung điểm của $EF$. Tìm quỹ tích điểm $H$ khi $I$ và $J$ di động trên đường thẳng $BC$.
Nhận xét: với em, bài này khó

Mệt , phù ......
Bài làm:
AM $\cap$ (O) ={M'}
vẽ đường tròn ngoại tiếp $\Delta OM'M$ , tâm là O' ,BC $\cap $(O') tại G
Dễ tháy $\angle GMO =90^o$
$\rightarrow $G,O',O thẳng hàng
Sau đó CM EF đi qua G ( cái này mình chưa cm dc nhưng đảm bảo đúng, đã test rất nhiều )
$\rightarrow \angle GHO =\angle GM'O =90^o$
$\rightarrow H \in (O')$
mà $(O') :\text{cố định}$
$\rightarrow$ H chuyển động trên (O')
2, Giới hạn :
$I \equiv J thì H \equiv M$
$I \equiv B , C \equiv J ,.....$

Hình gửi kèm

• 

Bài viết đã được chỉnh sửa nội dung bởi Tru09: 24-07-2012 - 21:38

[L Lawliet]

Bài 47: Cho tam giác $ABC$ nội tiếp đường tròn $(O)$, gọi $M$ là trung điểm của $BC$. Trên đường thẳng $BC$ lấy hai điểm $I$, $J$ đối xứng với nhau qua $M$. Gọi $E$, $F$ lần lượt là giao điểm thứ hai của $AI$, $AJ$ với đường tròn $(O)$ và $H$ là trung điểm của $EF$. Tìm quỹ tích điểm $H$ khi $I$ và $J$ di động trên đường thẳng $BC$.
Nhận xét: với em, bài này khó

Nợ topic cái hình trả sau nhé
----
Phần thuận:
Gọi $N$ là giao điểm thứ hai của tia $AM$ với đường tròn $(O)$.
Với $AB=AC$, dễ dàng thấy quỹ tích cần tìm là các điểm trong của đoạn thẳng $AN$.
Với $AB\neq AC$, ta giả sử $AB<AC$. Ta có $EF$ không song song với $BC$ mà cắt $BC$ tại $K$. Qua $F$ kẻ đường thẳng song song với $BC$ cắt $AE$, $AN$ tương ứng tại các điểm $P$, $Q$.
Ta có: $\frac{IM}{PQ}=\frac{AM}{AQ}=\frac{MJ}{QF}$ mà $IM=MJ$ nên $PQ=QF$ và $Q$ là trung điểm của $PF$.
Hơn nữa, theo giả thuyết thì $H$ là trung điểm của $EF$ nên $QH$ là đường trung bình của tam giác $FPE$ do đó $\widehat{QHF}=\widehat{PEF}$ (đồng vị). Mà $\widehat{PEF}=\widehat{QNF}$, nên $\widehat{QHF}=\widehat{QNF}$, suy ra tứ giác $QHNF$ nội tiếp, do đó $\widehat{NHF}=\widehat{NQF}$. Mặt khác $\widehat{NQF}=\widehat{NMC}$ (đồng vị), nên $\widehat{NHF}=\widehat{NMC}$, suy ra tứ giác $NHMK$ nội tiếp được. $(1)$
Do $M$, $H$ là các trung điểm của $BC$, $EF$ nên $\widehat{OMK}=\widehat{OHK}=90^o$ và tứ giác $OMKH$ nội tiếp được. $(2)$
Từ $(1)$, $(2)$ suy ra năm điểm $O$, $M$, $H$, $N$, $K$ nằm trên đường tròn đường kính $OK$. Do $M$, $N$, $O$ cố định nên đường tròn cố định và $K$ cố định. Gọi $S$ là trung điểm của $OK$, ta có $S$ cố định, $OS$ không đổi và $H$ thuộc đường tròn $(S)$ tâm $S$ bán kính $OS$. Gọi $D$ là giao điểm thứ hai của $(S)$ với đường tròn $(O)$, do $H$ là trung điểm của dây $EF$ nên $H$ nằm bên trong đường tròn $(O)$ và do đó $H$ chỉ nằm trên cung $DON$.
Phần đảo:
Đảo lại, lấy điểm $H_1$ trên cung $DON$, gọi $E_1$, $F_1$ là các giao điểm của $H_1K$ với đường tròn $(O)$ ($F_1$ nằm giữa $H_1$ và $K$), ta có $\widehat{OH_1K}=90^o$ nên $H_1$ là trung điểm của $E_1F_1$.
Gọi $I_1$ là giao điểm của $AE_1$ với $BC$, $J'$ là điểm đối xứng với $I_1$ qua $M$; $F'$ là giao điểm thứ hai của tia $AJ'$ với đường tròn $(O)$. Theo phần thuận, ta có $F'$, $E_1$, $K$ thẳng hàng, nên giao điểm thứ hai của $KE_1$ với đường tròn $(O)$ trùng với $F_1$, hay $H_1$ là một điểm của quỹ tích đang xét.
Vậy quỹ tích là cung $DON$ của đường tròn $(S)$ trong đó $K$, $N$, $S$, $D$ được xác định như ở trên.

Bài viết đã được chỉnh sửa nội dung bởi L Lawliet: 24-07-2012 - 21:42

[L Lawliet]

Bài 48: Giả sử $AA'$, $BB'$, $CC'$ là các đường phân giác trong của tam giác $ABC$. Gọi $L$ là giao điểm của $AA'$ và $B'C'$, $K$ là giao điểm của $CC'$, $A'B'$. Chứng minh rằng: $BB'$ là phân giác của góc $KBL$.

Bài viết đã được chỉnh sửa nội dung bởi L Lawliet: 30-08-2012 - 19:43

[ntm1406]

Bài 49: Trong hình vuông ABCD vẽ nửa đường tròn đường kính AD và vẽ cung AC có tâm D. Nối D với điểm P bất kỳ trên cung AC. DP cát đường tròn đường kính AD ở K. CMR: PK bằng khoảng cách từ P đến cạnh AB

Bài viết đã được chỉnh sửa nội dung bởi ntm1406: 25-07-2012 - 22:52

[triethuynhmath]

Bài 49: Trong hình vuông ABCD vẽ nửa đường tròn đường kính AD và vẽ cung AC có tâm D. Nối D với điểm P bất kỳ trên cung AC. DP cát đường tròn đường kính AD ở K. CMR: PK bằng khoảng cách từ P đến cạnh AB

Chém bài này.Gọi T là chân đường vuông góc kẻ từ P lên AB.
Ta có :
$\angle AKD=90^0$(góc nt chắn nửa đường tròn)
$\Rightarrow \angle AKP=90^0$
DDCM AT là tiếp tuyến của (D) và đường tròn đường kính AD
Xét đường tròn đường kính AD,AT là tiếp tuyến $\Rightarrow \angle TAK=\angle ADK,$
Xét đường tròn (D) có AT là tiếp tuyến $\Rightarrow \angle TAP=\frac{1}{2}\angle ADK\Rightarrow \angle TAP=\frac{1}{2}\angle TAK\Rightarrow \angle TAP=\angle PAK$
$\Rightarrow \Delta PAK=\Delta TAK(ch,gn)$ $=>PK=PT=>Q.E.D$
Đây là hình vẽ bổ sung:

Hình gửi kèm

• 

Bài viết đã được chỉnh sửa nội dung bởi triethuynhmath: 26-07-2012 - 15:37

[Mai Duc Khai]

Bài 50: Cho $D$ là điểm trong của $\Delta ABC $. Ba đường thẳng $AD,BD,CD$ cắt các cạnh $BC,AC,AB$ tương ứng tại $X,Y,Z$. Chứng minh rằng nếu hai trong ba tứ giác $ DYAZ, DZBX, DXCY$ có thể ngoại tiếp đường tròn thì tứ giác thứ ba cũng thế.

[chinhanh9]

Bài 51: Cho tam giác $ABC$, $D$ là một điểm nằm trong tam giác. Đường thẳng bất kì qua $A$ cắt $\left ( ABD \right )$ và $\left ( ACD\right )$ tại $M$ và $N$.$MB, NC$ cắt nhau tại $P$.
Tìm quỹ tích điểm $P$.

Bài viết đã được chỉnh sửa nội dung bởi nguyentrunghieua: 19-10-2013 - 22:56

[BlackSelena]

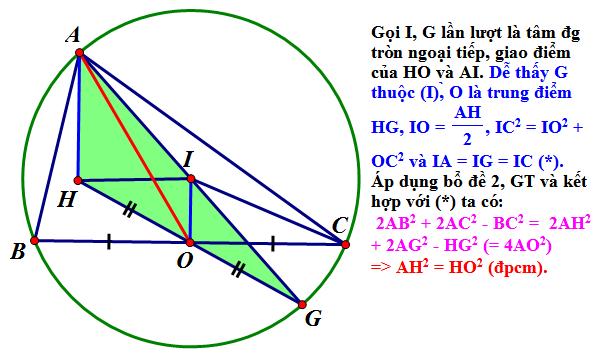
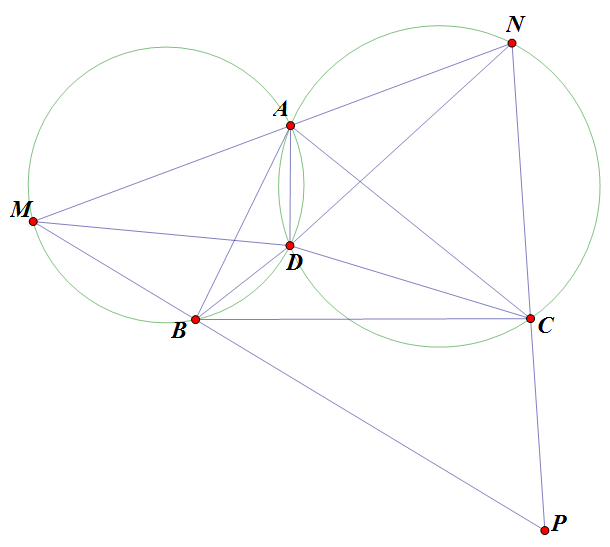
Bài 48:

(nhờ có anh L Lawliet gợi ý mới ra)
Lần lượt kẻ $LL_1 // BB' // KK_1$
Ta có
$\frac{BK_1}{BA'} = \frac{B'K}{B'A'}$
$\frac{KK_1}{BB'} = \frac{KA'}{B'A'}$
$\Rightarrow \frac{BK_1}{KK_1}. \frac{BB'}{BA'} = \frac{B'K}{B'A'}. \frac{B'A'}{A'K}$
$\Rightarrow \frac{BK_1}{KK_1} = \frac{B'K}{A'K}.\frac{BA'}{BB'}$
Mà mặt khác ta cũng có
$\frac{B'K}{A'K} = \frac{CB'}{CA'}$
$\Rightarrow \frac{BK_1}{KK_1} = \frac{CB'}{CA'} . \frac{BA'}{BB'}$
Mà $CB' =\frac{BC.AB}{AB+BC}$
$\frac{BA'}{CA'} = \frac{AB}{AC}$
Đặt $AB=c, BC = a, AC= b$ cho tiện.
$\Rightarrow \frac{BK_1}{KK_1} = \frac{ab}{a+c}.\frac{c}{b}.\frac{1}{BB'}$
Tương tự như thế ta cũng có
$\frac{BL_1}{LL_1}= \frac{ac}{a+c}$
Vậy $\frac{BK_1}{KK_1} = \frac{BL_1}{KK_1}$
Dễ thấy $\angle C'L_1L = \angle A'K_1K$
$\Rightarrow \angle BL_1L = \angle BK_1K$
$\Rightarrow \triangle BL_1L \sim \triangle BK_1K$
$\Rightarrow đpcm$
Đây là bổ đề hay đó

[Beautifulsunrise]

Bài 50: Cho $D$ là điểm trong của $\Delta ABC $. Ba đường thẳng $AD,BD,CD$ cắt các cạnh $BC,AC,AB$ tương ứng tại $X,Y,Z$. Chứng minh rằng nếu hai trong ba tứ giác $ DYAZ, DZBX, DXCY$ có thể ngoại tiếp đường tròn thì tứ giác thứ ba cũng thế.

[perfectstrong]

Bài 51: Cho tam giác $ABC$, $D$ là một điểm nằm trong tam giác. Đường thẳng bất kì qua $A$ cắt $\left ( ABD \right )$ và $\left ( ACD\right )$ tại $M$ và $N$.$MB, NC$ cắt nhau tại $P$.
Tìm quỹ tích điểm $P$.

Dùng kiến thức hơi mạnh chút để giải tổng quát. Nếu ai thích thì có thể giải lại theo cách lớp 9 dựa vào cách này cũng được
Lời giải:

Chú ý các bộ điểm $(M,A,D,B);(N;A;D;C)$ đồng viên.
\[
\begin{array}{l}
\left( {PB;PC} \right) = \left( {PB;BD} \right) + \left( {BD;CD} \right) + \left( {CD;PC} \right)\left( {\bmod \pi } \right) \\
= \left( {AM;AD} \right) + \left( {DB;DC} \right) + \left( {AD;AN} \right)\left( {\bmod \pi } \right) \\
= \left( {AM;AN} \right) + \left( {DB;DC} \right) = \left( {DB;DC} \right)\left( {\bmod \pi } \right) \\
\end{array}
\]
Do đó, $D,B,P,C$ đồng viên hay quỹ tích $P$ là đường tròn ngoại tiếp $\vartriangle DBC$.

[chinhanh9]

Bài 52: (Một bài toán cũ mình chế ra đã bị đẩy xuống trang 5)
Cho đường tròn (O) nội tiếp tam giác ABC. M, N, P lần lượt là các tiếp điểm trên AB, AC và BC. Các đường thẳng MN và BC cắt nhau tại điểm D. Qua D vẽ tiếp tuyến của (O) cắt AB, AC theo thứ tự tại E và F. Chứng minh: AP, BF, CE đồng quy.
----------------------------------------
P/S: giải bài 40 đi các bạn

Bài viết đã được chỉnh sửa nội dung bởi binhmetric: 27-07-2012 - 08:45

[NLT]

Bài 53:
Cho $A$ và $C$ là $2$ điểm cố định, đường tròn $(O)$ đi qua $2$ điểm $A,C$. Điểm $B$ cố định trên đoạn $AC$. Gọi $P$ là giao điểm của các tiếp tuyến của $(O)$ tại các điểm $A$ và $C$. $PB$ cắt $(O)$ tại các điểm $Q$ và$Q'$ ($Q$ nằm trên đoạn $PB$). Phân giác của góc $\angle AQC$ cắt $AC$ tại $R$.

$a)$ Chứng minh rằng $R$ cố định khi đường tròn $(O)$ thay đổi.

$b)$ Gọi $P'$ là giao điểm các tiếp tuyến với đường tròn $(O)$ tại các điểm $Q$ và $Q'$. Chứng minh rằng $P'$ cố định khi $(O)$ thay đổi.

___

[Beautifulsunrise]

Bài 52: (Một bài toán cũ mình chế ra đã bị đẩy xuống trang 5)
Cho đường tròn (O) nội tiếp tam giác ABC. M, N, P lần lượt là các tiếp điểm trên AB, AC và BC. Các đường thẳng MN và BC cắt nhau tại điểm D. Qua D vẽ tiếp tuyến của (O) cắt AB, AC theo thứ tự tại E và F. Chứng minh: AP, BF, CE đồng quy.
----------------------------------------
P/S: giải bài 40 đi các bạn

Bài viết đã được chỉnh sửa nội dung bởi binhmetric: 27-07-2012 - 10:38

[Beautifulsunrise]

Bài 53:
Cho $A$ và $C$ là $2$ điểm cố định, đường tròn $(O)$ đi qua $2$ điểm $A,C$. Điểm $B$ cố định trên đoạn $AC$. Gọi $P$ là giao điểm của các tiếp tuyến của $(O)$ tại các điểm $A$ và $C$. $PB$ cắt $(O)$ tại các điểm $Q$ và$Q'$ ($Q$ nằm trên đoạn $PB$). Phân giác của góc $\angle AQC$ cắt $AC$ tại $R$.

$a)$ Chứng minh rằng $R$ cố định khi đường tròn $(O)$ thay đổi.

$b)$ Gọi $P'$ là giao điểm các tiếp tuyến với đường tròn $(O)$ tại các điểm $Q$ và $Q'$. Chứng minh rằng $P'$ cố định khi $(O)$ thay đổi.

___

Bài viết đã được chỉnh sửa nội dung bởi binhmetric: 27-07-2012 - 22:42

[perfectstrong]

Không cần phải tới hàng điều hòa đâu bác
Chỉ đơn giản là 1 tính chất trong tứ giác ngoại tiếp:
Cho tứ giác $ABCD$ ngoại tiếp $(O)$, có các tiếp điểm trên $AB,BC,CD,DA$ tương ứng là $M,N,P,Q$. Khi đó, $AC,BD,MP,NQ$ đồng quy tại $I$.

[Tru09]

Bài 52 :
Có thể làm = cách cm như sau đc không?
Theo menelous:
$\frac{DB}{DC}.\frac{CF}{FA}.\frac{AE}{EB}=1$
$DPCM \leftrightarrow \frac{CF}{FA}.\frac{AE}{EB}.\frac{BP}{PC}=1$
Vậy ta cần cm $:\frac{DB}{DC}=\frac{BP}{PC}$
các bạn CM tiếp nhé

[Cao Xuân Huy]

Dùng kiến thức hơi mạnh chút để giải tổng quát. Nếu ai thích thì có thể giải lại theo cách lớp 9 dựa vào cách này cũng được
Lời giải:

Chú ý các bộ điểm $(M,A,D,B);(N;A;D;C)$ đồng viên.
\[
\begin{array}{l}
\left( {PB;PC} \right) = \left( {PB;BD} \right) + \left( {BD;CD} \right) + \left( {CD;PC} \right)\left( {\bmod \pi } \right) \\
= \left( {AM;AD} \right) + \left( {DB;DC} \right) + \left( {AD;AN} \right)\left( {\bmod \pi } \right) \\
= \left( {AM;AN} \right) + \left( {DB;DC} \right) = \left( {DB;DC} \right)\left( {\bmod \pi } \right) \\
\end{array}
\]
Do đó, $D,B,P,C$ đồng viên hay quỹ tích $P$ là đường tròn ngoại tiếp $\vartriangle DBC$.

Cho em xài lại hình. Em không rõ thế này có được không.
Lời giải:
Thuận:
Ta có:
\[\widehat {MBD} + \widehat {NCD} = \widehat {MBD} + \left( {{{180}^o} - \widehat {DAN}} \right) = \widehat {MBD} + \widehat {MAD} = {180^o}\]
Do đó:
\[\widehat {DBP} + \widehat {DCP} = {360^o} - \left( {\widehat {MBD} + \widehat {NCD}} \right) = {180^o}\]
Vì thế $BDCP$ là tứ giác nội tiếp nên $P$ nằm trên đường tròn ngoại tiếp tam giác $BDC$
Đảo:
Lấy điểm P trên đường tròn ngoại tiếp tam giác $BDC$. $PB,PC$ cắt đường tròn ngoại tiếp tam giác $DAB,DAC$ tại $M,N$.
Ta có:
\[\widehat {MAD} = \widehat {PBD};\widehat {NAD} = \widehat {DCP}\]
Mà: $\widehat {PBD} + \widehat {DCP} = {180^o}$ nên $M,A,N$ thẳng hàng
Vậy quĩ tích của $P$ là ...