Bài 1. (2,5 điểm)
Cho biểu thức $P = \frac{\sqrt{n+1}-1}{\sqrt{n+1}+1}+\frac{\sqrt{n+1}+3}{\sqrt{n+1}-3}-\frac{n-\sqrt{n+1}+7}{n-2\sqrt{n+1}-2}$ với $n\in \mathbb{N},n\neq 8$
a/ Rút gọn biểu thức $Q=\frac{P}{n+3\sqrt{n+1}+1}$ với $n\in \mathbb{N},n\neq 8$
b/ Tìm tất cả các giá trị n ( $n\in \mathbb{N},n\neq 8$ ) sao cho P là một số nguyên tố.
1a/ $P=\frac{\sqrt{x+1}}{\sqrt{x+1}-3}=>Q=\frac{1}{x-8}$
1b/ P = 2 là số nguyên tố khi n = 35
Bài 2. (2,0 điểm)
a/ Tìm x, biết: $2\sqrt{x+4}-4\sqrt{2x-6}=x-7$
b/ Giải hệ phương trình: $\left\{\begin{matrix} x+6=4\sqrt{y-4}\\ y+10=6\sqrt{z-9}\\ z-16=2\sqrt{x-1} \end{matrix}\right.$
2a/
$2\sqrt{x+4}-4\sqrt{2x-6}=x-7 \Leftrightarrow 2(\sqrt{x+4}-3)-4 \left ( \sqrt{2x-6}-2 \right )=x-5 \Leftrightarrow \frac{2(x-5)}{\sqrt{x+4}+3}-\frac{8(x-5)}{\sqrt{2x-6}+2}=x-5 \Leftrightarrow \begin{bmatrix} x=5\\ \frac{1}{\sqrt{x+4}+3}=1+\frac{8}{\sqrt{2x-6}+2} \end{bmatrix}$
Cách khác : đặt $\sqrt{x+4}=a,\sqrt{2x-6}=b \Rightarrow x-7 = b^2-a^2 + 3$
$\Rightarrow b^2 - a^2 + 3 = 2a - 4b \Leftrightarrow (b+2)^2=(a+1)^2$
Giải ra rồi đối chiếu đk + thử lại ta được x = 5
2b/
[/center]
Cộng theo vế 3 pt ta được:
$x+y+z=4\sqrt{y-4}+6\sqrt{z-9}+2\sqrt{x-1}$
$\Leftrightarrow x-1-2\sqrt{x-1}+1+y-4-4\sqrt{y-4}+4+z-9-6\sqrt{z-9}+9=0$
$\Leftrightarrow (\sqrt{x-1}-1)^{2}+(\sqrt{y-4}-2)^{2}+(\sqrt{z-9}-3)^{2}=0$
Đến đây cho từng bình phương bằng 0 là tìm được nghiệm
Bài 3. (2,0 điểm)
a/ Cho hàm số bậc nhất $y = ax + b$ có đồ thị đi qua điểm M(1;4). Biết rằng đồ thị của hàm số đã cho cắt trục Ox tại điểm P có hoành độ dương và cắt trục Oy tại điểm Q có tung độ dương. Tìm a và b sao cho OP + OQ nhỏ nhất ( với O là gốc tọa độ )
b/ Tìm số tự nhiên có 2 chữ số. Biết rằng nếu lấy tổng của 2 chữ số ấy cộng với 3 lần tích của 2 chữ số ấy thì bằng 17.
Bài 3a)M thuộc $(d): y = ax + b$ nên $a + b = 4$ hay $ b = 4 - a.$ Khi đó: $(d): y = ax + 4 - a$
Theo đề, ta có $P(\frac{a-4}{a}; 0), Q(0; 4 - a)$ và $\frac{a - 4}{a} > 0; 4 - a > 0 \Rightarrow a < 0$
$OP + OQ = \frac{a - 4}{a} + 4 - a = - a - \frac{4}{a} + 5$
Vì $ a < 0$ nên $- a > 0; \frac{-4}{a} > 0$. Áp dụng BĐT Cauchy cho 2 số dương $ - a$ và $\frac{-4}{a} $ ta được: $OP + OQ \geq 2.2 + 5 = 9$
Khi đó $Min(OP + OQ) = 9 \Leftrightarrow a = - 2 , b = 6$
3b / như cách bạn banhgaongonngon
$a+b+3ab=17\Leftrightarrow 9ab+3a+3b=51\Leftrightarrow (3a+1)(3b+1)=52$
Bài 4. (2,0 điểm)
Cho tam giác ABC. Gọi I là tâm đường tròn nội tiếp tam giác ABC, qua I vẽ đường thẳng vuông góc với đường thẳng CI, đường thẳng này cắt các cạnh AC, BC lần lượt tại M và N.
a/ Chứng minh rằng hai tam giác IAM và BAI đồng dạng.
b/ Chứng minh rằng $\frac{AM}{BN}= \left ( \frac{AI}{BI} \right )^2.$

a/ $\widehat{IAM}+\widehat{IBN}+\widehat{MCI}=90^{\circ}$
$\widehat{IMC}+\widehat{MCI}=90^{\circ}$ $\Rightarrow \widehat{IAM}+\widehat{AIM}+\widehat{MCI}=90^o$
$\Rightarrow \widehat{ IBN} =\widehat{AIM}\Rightarrow \widehat{ABI}=\widehat{AIM}$
$\Rightarrow$ hai tam giác IAM và BAI đồng dạng.
b/ Chứng minh tương tự câu a => hai tam giác IBN và ABI đồng dạng
$\Rightarrow \left\{\begin{matrix} AM.AB=AI^2\\ BN.AB=BI^2 \end{matrix}\right.$
$\Rightarrow$ đpcm
Bài 5. (1,5 điểm)
Cho tam giác ABC có $\widehat{BAC}$ là góc tù. Vẽ các đường cao CD và BE của tam giác ABC ( D nằm trên đường thẳng AB, E nằm trên đường thẳng AC). Gọi M,N lần lượt là chân đường vuông góc của các điểm B và C trên đường thẳng DE. Biết rằng $S_{1}$ là diện tích tam giác ADE, $S_{2}$ là diện tích tam giác BEM và $S_{3}$ là diện tích tam giác CDN. Tính diện tích tam giác ABC theo $S_{1},S_{2},S_{3}.$
Bài 5: Đã tìm được cách làm THCS 
Ta sẽ chứng minh $S_{ABC}=S=S_1+S_2+S_3 \quad (1)$. Thật vậy:
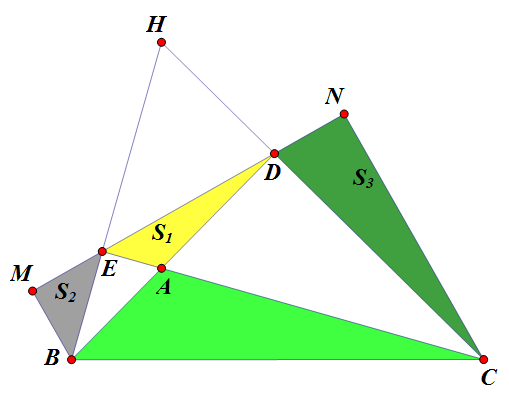
Dễ chứng minh rằng $ME=ND$ (bằng cách lấy thêm trung điểm $MN,BC$).
\[
\begin{array}{l}
S = S_{MNBC} - S_{BMD} - S_{CNE} + S_1 \\
\Rightarrow S - S_1 = S_{MNBC} - S_{BMD} - S_{CNE} \\
\end{array}
\]
Cho nên (1) tương đương với\[
\begin{array}{l}
S_2 + S_3 = S_{MNBC} - S_{BMD} - S_{CNE} \\
\Leftrightarrow S_{MNBE} = \left( {S_2 + S_{BMD} } \right) + \left( {S_3 + S_{CNE} } \right) = \frac{1}{2}MB\left( {ME + MD} \right) + \frac{1}{2}CN\left( {ND + NE} \right) \\
\Leftrightarrow S_{MNBE} = \frac{1}{2}MB\left( {ND + MD} \right) + \frac{1}{2}CN\left( {ME + NE} \right) = \frac{1}{2}\left( {MB + CN} \right)MN \\
\end{array}
\]
Đẳng thức cuối luôn đúng nên (1) được chứng minh.
Cách dùng đồng dạng :
$\Delta BEM$ đồng dạng $\Delta BCD$
$\Rightarrow \frac{S_{2}}{S_{BCD}}=\frac{BE^2}{BC^2}$
$\Rightarrow \frac{S_{2}}{S+S_{ADC}}=\frac{BE^2}{BC^2}(1)$
$\Delta ECN$ đồng dạng $\Delta BCD$
$\Rightarrow \frac{S_{ECN}}{S_{BCD}}=\frac{EC^2}{BC^2}$
$\Rightarrow \frac{S_{1}+S_{3}+S_{ADC}}{S+S_{ADC}}=\frac{EC^2}{BC^2}(2)$
$(1),(2) \Rightarrow \frac{S_{1}+S_{2}+S_{3}+S_{ADC}}{S+S_{ADC}}=1 \Rightarrow S_{BAC}=S_{1}+S_{2}+S_{3}$
Cách khác :

Chứng minh $S_{BEC}+S_{CDB}=HK . BC$
Chứng minh $S_{IHM}=S_{FHN}$
BIFC là hình bình hành
Chứng minh $S_{IFCB}=S_{MNCB}=HK.BC$
$\Rightarrow S_{MNCB}=S_{BEC}+S_{CDB}$
$\Rightarrow S_{BAC}=S_{1}+S_{2}+S_{3}$

















