bachocdien nội dung
Có 47 mục bởi bachocdien (Tìm giới hạn từ 20-04-2020)
#407176 Tính tổng một dãy hội tụ nhanh hơn (Phần 2)
 Đã gửi bởi
bachocdien
on 23-03-2013 - 11:09
trong
Toán học lý thú
Đã gửi bởi
bachocdien
on 23-03-2013 - 11:09
trong
Toán học lý thú
Nếu ta lấy phương trình (6), thay thế $n$ bằng $n-1$ thì ta được
$S=S_{n-1}+\frac{B_{0}}{n-1}+\frac{B_{1}}{(n-1)^{2}}+\frac{B_{2}}{(n-1)^{3}}+...$ (7)
Do đó
$S_{n-1}-S_{n}=B_{0}(\frac{1}{n}-\frac{1}{n-1})+B_{1}(\frac{1}{n^{2}}-\frac{1}{(n-1^{2})})+...$ (8)
Từ định nghĩa $S_{n}-S_{n-1}=\frac{1}{n^{2}}$
Kết hợp 2 phương trình trên ta được
$\frac{1}{n^{2}}=B_{0}(\frac{1}{n}-\frac{1}{n-1})+B_{1}(\frac{1}{n^{2}}-\frac{1}{(n-1^{2})})+...$ (9)
Ta có thể tìm giá trị của từng $B_{k}$ bằng cách mở rộng các biểu thức có lũy thừa của $\frac{1}{n}$ với$n$ rất lớn. Ví dụ:
$\frac{1}{n-1}=\frac{1}{n(1-\frac{1}{n})}=\frac{1}{n}+\frac{1}{n^{2}}+\frac{1}{n^{3}}+...$
và
$\frac{1}{(n-1)^{2}}=\frac{1}{n^{2}(1-\frac{1}{n})^{2}}=\frac{1}{n^{2}}+\frac{2}{n^{3}}+\frac{3}{n^{4}}+...$
Tổng quát:
$\frac{1}{(n-1)^{k}}=\frac{1}{n^{k}(1-\frac{1}{n})^{k}}=\frac{1}{n^{k}}+\frac{k}{n^{k+1}}+\frac{k+1}{n^{k+2}}+...+\frac{\begin{pmatrix} k+r-1\\ r \end{pmatrix}}{n^{k+r}}+...$
Ở đây, $\begin{pmatrix} k+r-1\\ r \end{pmatrix}=\frac{k(k+1)...(k+r-1)}{r!}$
Những khai triển trên chính là Khai triển Taylor. Bây giờ ta kết hợp những khai triển trên vào phương trình (9):
$\frac{1}{n^{2}}=B_{0}(\frac{1}{n^{2}}+\frac{1}{n^{3}}+...)+B_{1}(\frac{2}{n^{3}}+\frac{3}{n^{4}}+...)+...+B_{k-1}(\frac{k}{n^{k+1}}+\frac{k(k+1)}{2n^{k+2}}+...+\begin{pmatrix} k+r-1\\ r \end{pmatrix}\frac{1}{n^{k+r}}+...)+...$ (10)
sử dụng phương pháp cân bằng hệ số ta có thể tìm được các giá trị của $B_{r}$
$B_(0)=1$
$B_{0}+2B_{1}=0$
$B_{0}+3B_{1}+3B_{2}=0$
Thế giá trị của $B_{0}$ vào các biểu thức dưới ta tìm được $B_{1}=\frac{-1}{2}, B_{2}=\frac{1}{6}$
Tiếp tục như thế ta tính được tất cả các giá trị của $B_{r}$
$B_{k-1}=\frac{-1}{k}(\binom{k}{2}B_{k-2}+\binom{k}{3}B_{k-3}+...+B_{0})$
Ta nhận thấy rằng nếu $k$ là số lẻ lớn hơn 1 thì $B_{k}=0$. Những con số mà chúng ta tính đều khá nhỏ và tăng rất nhanh khi tăng $k$. Chúng được gọi là số Bernoulli, chúng xuất hiện ở nhiều nơi, từ lý thuyết số đến cơ học. Jakob Bernoulli đã miêu tả chúng trng cuốn sách Ars Conjectandi-xuất bản năm 1713. Kể từ đó chúng chiếm 1 vai trò quan trọng trong lịch sử toán học. Ví dụ, chúng rất quan trọng trong việc hiểu được định lý lớn Fermat...
Trở lại với bài toán ban đầu, ta có;
$E_{n,k}=\frac{B_{0}}{n}+\frac{B_{1}}{n^{2}}+...+\frac{B_{k-1}}{n^{2}}$ (13)
$S\approx S_{n}+E_{n,k}$
Ví dụ lấy $n=k=10$ thì:
$S=S_{n}+\frac{1}{n}-\frac{1}{2n^{2}}+\frac{1}{6n^{3}}-\frac{1}{30n^{5}}+\frac{1}{42n^{7}}-\frac{1}{30n^{9}}+\alpha (\frac{1}{n^{11}})$
Số hạng cuối cùng chính là sai số của phép tính. Với 10 số hạng ta có sai số cỡ $10^{-11}$-một sự cải thiện tuyệt vời so với cách tính cũ.
Nguồn: http://plus.maths.or...dd-quickly#skip
#407149 Tính tổng một dãy hội tụ nhanh hơn (Phần 1)
 Đã gửi bởi
bachocdien
on 22-03-2013 - 23:58
trong
Toán học lý thú
Đã gửi bởi
bachocdien
on 22-03-2013 - 23:58
trong
Toán học lý thú

Một trong những kết quả toán học yêu thích nhất của tôi( tác giả Chris Budd) là phương trình nổi tiếng
Theo những gì tôi đang quan tâm, thì toán học chính là đây, và nếu phương trình này không chinh phục được bạn thì đơn giản chỉ vì bạn không có tâm hồn. Cái mà phương trình này đã làm là kết nối 2 khái niệm hoàn toàn khác nhau, một bên là số vô tỉ $\pi$, còn một bên là một chuỗi các phân số có mẫu số lẻ. Kết quả thực sự đáng kinh ngạc và có chút thần kì, và đó chính xác đã minh họa cho những thứ bất thường mà toán học có thể liên kết chúng với nhau. Bất cứ khi nào tôi được hỏi về định nghĩa thế nào là toán học tôi chỉ đơn giản viết phương trình trên ra-nếu những gì bạn nghĩ về toán đơn giản chỉ là ngôn ngữ thì hãy nghĩ lại đi.
Phương trình này có một lịch sử tuyệt vời. Nó bắt nguồn ở phương Tây năm 1671 bởi James Gregory từ công thức cho $arctan(x)$ và sau đó được độc lập tìm ra bởi Gottfried Leibniz. Tuy nhiên công thức tương tự( cùng với nhiều kết quả khác bao gồm những chuỗi vô hạn) đã được phát hiện từ trước những năm 30 bởi nhà toán học vĩ đạo người Ấn Độ Madhava. Kết quả tương tự của phương trình tuyệt đẹp này là 1 dãy vô hạn:
$\frac{\pi ^{2}}{6}=1+\frac{1}{2^{2}}+\frac{1}{3^{2}}+\frac{1}{4^{2}}+...$ (2)
$\frac{\pi ^{3}}{32}=1-\frac{1}{3^{3}}+\frac{1}{5^{3}}-\frac{1}{7^{3}}+...$ (3)
và
$\frac{\pi ^{4}}{90}=1+\frac{1}{2^{4}}+\frac{1}{3^{4}}+\frac{1}{4^{4}}+...$ (4)
Tuy nhiên, theo 1 nghĩa nào đó, những phương trình trên đã gây thất vọng. Nếu bạn thực sự muốn tính $\pi^{2}, \pi^{3}...$thì có lẽ bạn sẽ không dùng công thức nào trong số chúng-lý do là vì chúng hội tụ rất chậm. Nếu bạn lấy phương trình (1) với tổng của 100 số hạng và nhân với 4, bạn sẽ được $3.146567747182956...$, khá gần với giá trị chính xác nhưng chỉ đúng ở 2 chữ số thập phận. Nếu bạn muốn tính gần đúng đến 6 chữ số thập phân bạn sẽ phải thêm rất nhiều thừa số nữa, các lỗi làm tròn kết hợp với các tính toán sẽ làm độ chính xác giảm đi trầm trọng.
Vậy bạn có thể nói gì đây. Chắc chắn rằng bạn không cần phải biết chính xác giá trị của số $\pi$. Tuy nhiên số $\pi$ ngự trị trong mọi lĩnh vực của công nghệ, toán học…và có nhiều lĩnh vực( với đòi hỏi độ chính xác cao) sẽ cần giá trị của $\pi$ càng chính xác càng tốt. ví dụ trong công nghệ điện tử cao tần, với tần số khoảng 1GHz những kĩ sư điện tử sẽ phải làm việc với những hàm dạng $u(t)=cos(2\pi ft)$ $f$ xấp xỉ 10^9 và $t$ là 1 số gần tới 1. Để tính chĩnh xác hàm $u(t)$ cần cho các máy GPS cần một độ chính xác của $\pi$ cỡ $10^{15}$.
Vì vậy sống trong một thế giới hiện đại có nghĩa là ta cần biết giá trị của $\pi$ càng chính xác càng tốt.
Vậy chúng ta có thể làm gì?Có một cách là ta nhập thật nhiều số hạng trong dãy 1 vào 1 máy tính xịn và chờ đợi máy tính tính. Hoặc chúng ta có thể cố và tăng tốc độ hội tụ của nó. Vì vậy chỉ với một số lượng nhỏ số hạng( 10 chẳng hạn) ta có thể nhận được 10 số đáng kể cho $\pi$. Điều tuyệt vời này là những công thức mà một sinh viên năm nhất đại học hoặc 1 học sinh loại A hoàn toàn có thể hiểu được. Về nguyên tắc phương pháp này có thể được dùng để tính tổng những dãy hội tụ khác.
Xét dãy
$S_{n}=1+\frac{1}{2^{2}}+\frac{1}{3^{2}}+...+\frac{1}{n^{2}}$ (5)
$S_{n}\rightarrow S$ khi $n\rightarrow \infty $
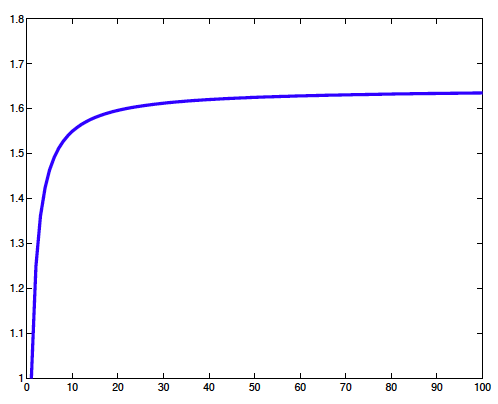
Đặt $E_{n}=S-S_{n}$ do đó $E_{n}\rightarrow 0$ khi $n\rightarrow \infty$
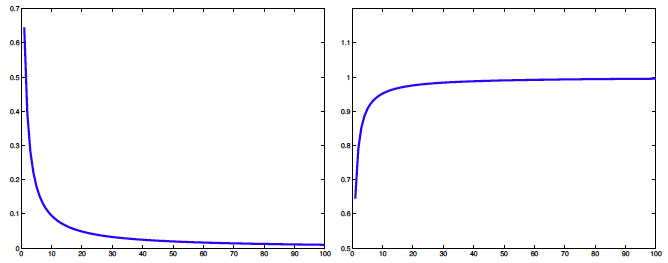
(Hình trái) Đồ thị $E_{n}$; (Hình phải) Đồ thị $nE_{n}$
Từ đây, ta có thể đoán rằng $E_{n}\approx \frac{1}{n}$, vì vậy
$S=S_{n}+\frac{1}{n}$
Chúng ta có thể cải thiện phép gần đúng này bằng cách giả sử có 1 dãy $B_{0},B_{1},B_{2},...$ với $n\rightarrow \infty$
$S=S_{n}+\frac{B_{0}}{n}+\frac{B_{1}}{n^{2}}+...$ (6)
Nếu có thể tính các giá trị của $B_{r}$ với $r=1,2,3,...,k$ thì có thể tính được $S$ từ $S_{n}$ bằng công thức
$S\approx S_{n}+\frac{B_{0}}{n}+\frac{B_{1}}{n^{2}}+...+\frac{B_{k-1}}{n^{k}}$
Nguồn: http://plus.maths.or...dd-quickly#skip
#404425 Điểm trên lục giác đều
 Đã gửi bởi
bachocdien
on 12-03-2013 - 14:48
trong
Tổ hợp - Xác suất và thống kê - Số phức
Đã gửi bởi
bachocdien
on 12-03-2013 - 14:48
trong
Tổ hợp - Xác suất và thống kê - Số phức
#404280 Tìm giá trị nhỏ nhất
 Đã gửi bởi
bachocdien
on 11-03-2013 - 22:03
trong
Bất đẳng thức và cực trị
Đã gửi bởi
bachocdien
on 11-03-2013 - 22:03
trong
Bất đẳng thức và cực trị
$25(x^{2}+y^{2})+(12-3x-4y)^{2}$
#404017 Cuộc thi Vật lý Online
 Đã gửi bởi
bachocdien
on 11-03-2013 - 14:48
trong
Các môn tự nhiên (Vật lý, Hóa học, Sinh học, Công nghệ)
Đã gửi bởi
bachocdien
on 11-03-2013 - 14:48
trong
Các môn tự nhiên (Vật lý, Hóa học, Sinh học, Công nghệ)
http://iep.hut.edu.v...ne/Chuyende.htm
#400382 Bài toán mở Iphone
 Đã gửi bởi
bachocdien
on 27-02-2013 - 12:52
trong
Tổ hợp - Xác suất và thống kê - Số phức
Đã gửi bởi
bachocdien
on 27-02-2013 - 12:52
trong
Tổ hợp - Xác suất và thống kê - Số phức


#399863 Japan Mathematical Olympiad Finals 2013
 Đã gửi bởi
bachocdien
on 25-02-2013 - 10:20
trong
Thi HSG Quốc gia và Quốc tế
Đã gửi bởi
bachocdien
on 25-02-2013 - 10:20
trong
Thi HSG Quốc gia và Quốc tế
1, nhóm 2..., nhóm k và mỗi nhóm có ít nhất 1 người. Chỉ ra rằng $n^{2}$ cái kẹo có thể được chia cho $n$ người sao cho thỏa mãn tất cả các điều kiện:
- Mỗi người có ít nhất 1 cái kẹo
- $a_{i}$ cái kẹo được chia cho mỗi người thuộc nhóm $i$ ($1\leq i\leq k$)
- Nếu $1\leq i< j\leq k$ thì $a_{i}>a_{j}$
$f(m)+f(n)=f(mn)+f(m+n+mn)$
nghiệm đúng $\forall m,n\in \mathbb{Z}$
Câu 3.Cho $n\geq 2$ là 1 số nguyên dương. Tìm giá trị nhỏ nhất của số nguyên dương $m$ để tồn tại các số nguyên dương $a_{1},a_{2},...,a_{n}$ sao cho:
- $a_{1}<a_{2}<...<a_{n}=m$
- $\frac{a_{1}^{2}+a_{2}^{2}}{2},\frac{a_{2}^{2}+a_{3}^{2}}{2},...,\frac{a_{n-1}^{2}+a_{n}^{2}}{2}$ đều là số chính phương
Câu 5.Cho $n$ là số nguyên dương. Lấy các điểm $P_{1},P_{2},...,P_{4n}$ sao cho không có 3 điểm nào thẳng hàng. Cho $i=1,2,...4n$, phép quay tâm $P_{i}$, góc $-90^{0}$ biến đoạn $P_{i}P_{i-1}$ thành $P_{i}P_{i+1}$.Tìm giá trị lớn nhất của số cặp $(i,j)$, sao cho $P_{i}P_{i+1}$ và $P_{j}P_{j+1}$ cắt nhau, không tính các điểm mút.
Chú ý: $P_{0}=P_{4n}, P_{4n+1}=P_{1}$ và $1\leq i< j\leq 4n$
#399825 Sử dụng Vật lý để chứng minh Toán học
 Đã gửi bởi
bachocdien
on 24-02-2013 - 22:11
trong
Các môn tự nhiên (Vật lý, Hóa học, Sinh học, Công nghệ)
Đã gửi bởi
bachocdien
on 24-02-2013 - 22:11
trong
Các môn tự nhiên (Vật lý, Hóa học, Sinh học, Công nghệ)
Chứng minh toán học của định lý này thì đã có rất nhiều. Sau đây là 1 lời giải rất vật lý(Cách chứng minh của M.Levi)
Xét 1 cái hộp hình lăng trụ đứng có đáy tam giác vuông với độ dài các cạnh lần lượt là a,b,c (c là cạnh huyền), chiều cao h.
Ta đổ nước vào hộp đến chiều cao h, cái hộp không quay cũng không dịch chuyển.
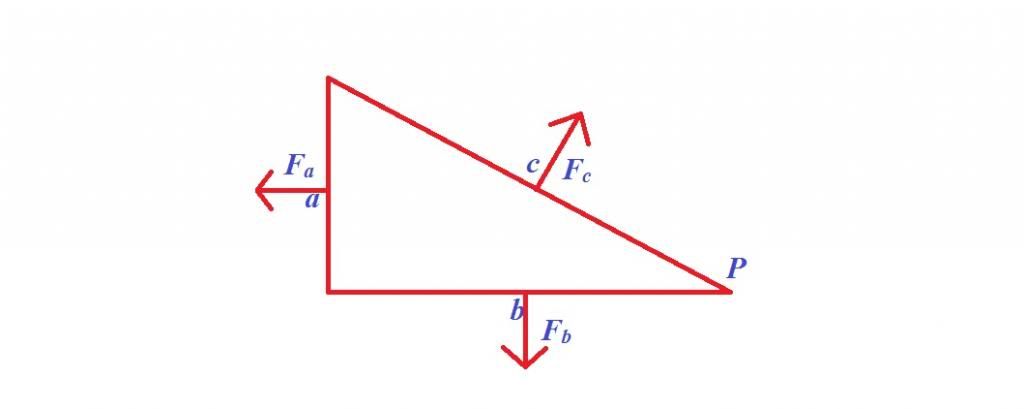
Các lực tác dụng lên vách hộp là:
$F_{a}=p.S_{a}=p.h.a$
$F_{b}=p.S_{b}=p.h.b$
$F_{c}=p.S_{c}=p.h.c$
Vì cái hộp nằm yên không quay nên tổng mô men lực với trục quay đi qua P là bằng 0
$F_{a}.\frac{a}{2}+F_{b}.\frac{b}{2}=F_{c}.\frac{c}{2}$
$\Leftrightarrow a^{2}+b^{2}=c^{2}$
2. Bài toán tìm điểm Toricelli
Cho tam giác ABC tìm điểm M nằm bên trong tam giác sao cho tổng MA+MB+MC nhỏ nhất.
Ta sẽ xây dựng 1 mô hình cơ học như sau: 3 ròng rọc cố định tại A,B,C 3 dây nối vắt qua 3 ròng rọc, được nối với nhau tại M. 3 vật nặng khối lượng bằng nhau.
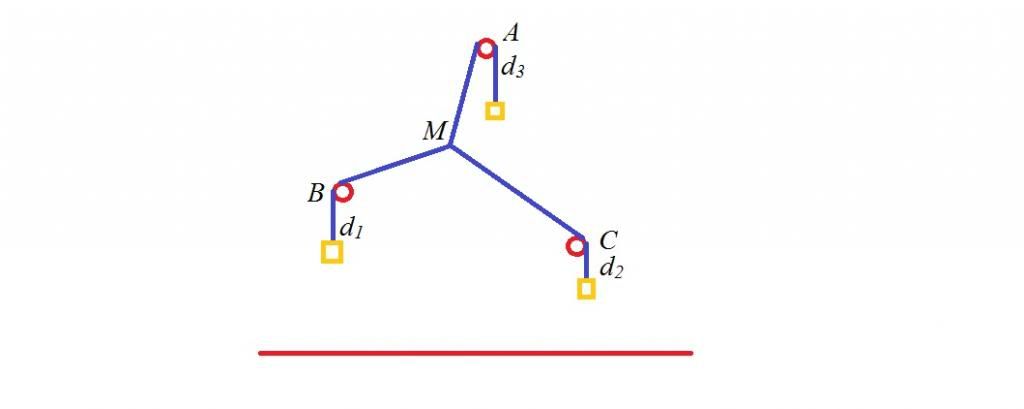
Hệ cân bằng $\Leftrightarrow$ Năng lượng của hệ đạt cực tiểu, ở đây là thế năng hấp dẫn đạt cực
$\Leftrightarrow h_{1}+h_{2}+h_{3}$ min ($h_{1}, h_{2}, h_{3}$ là khoảng cách từ các vật nặng tới mặt đất)
$\Leftrightarrow d_{1}+d_{2}+d_{3}$ max
$\Leftrightarrow MA+MB+MC$ min
Mặt khác, hệ cân bằng, lực căng dây là như nhau( 3 vật nặng giống nhau)
$\Rightarrow $ 3 lực sẽ đôi một tạo thành những góc bằng nhau bằng $120^{0}$
Ta cũng có thể mở rộng bài toán với n điểm với cách làm tương tự.
3. Bài toán đẳng chu
Chứng minh rằng trong các hình có cùng chu vi thì hình tròn là hình có diện tích lớn nhất.
Ta sẽ sử dụng tính chất của sức căng mặt ngoài
Ta tạo một màng xà phong bằng 1 khung chữ nhật. bên trong khung có 1 dây chỉ như hình vẽ.
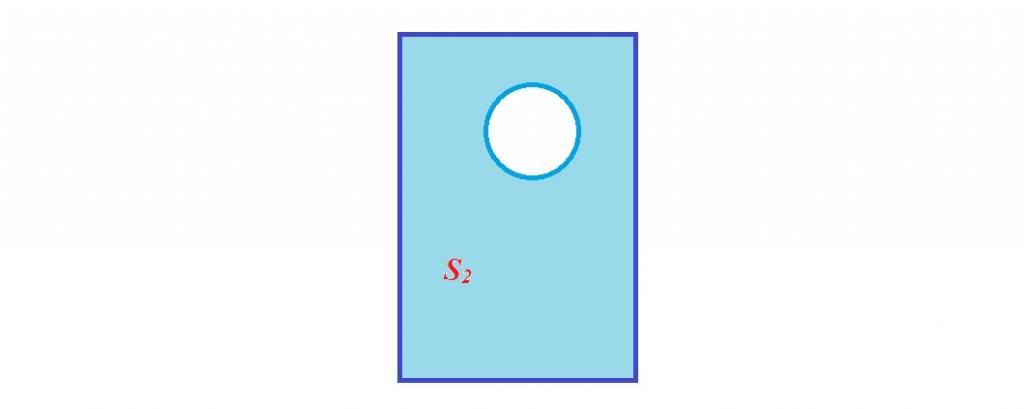
Ban đầu có cả xà phòng trong dây chỉ và ngoài dây, dây sẽ có dạng méo mó nào đấy. Sau đó chọc thủng màng xà phòng bên trong dây chỉ
$\Rightarrow$ dây có dạng hình tròn.
Ta biết rằng năng lượng của màng xà phòng tỉ lệ thuận với diện tích của nó.
$\Rightarrow$ để năng lượng của màng xà phòng nhỏ nhất( bền nhất) thì diện tích $S_{2}$ phải nhỏ nhất
$\Rightarrow$ diện tích của vòng dây là lớn nhất( do diện tích cả hình chữ nhật không đổi)
$\Rightarrow$ trong các hình có cùng chu vi hình tròn có diện tích lớn nhất.
#394225 Số nguyên tố Mersenne thứ 48
 Đã gửi bởi
bachocdien
on 07-02-2013 - 09:36
trong
Tin tức - Vấn đề - Sự kiện
Đã gửi bởi
bachocdien
on 07-02-2013 - 09:36
trong
Tin tức - Vấn đề - Sự kiện
Marin Mersenne (1588-1648), đã thực hiện một phỏng đoán nổi tiếng: với những giá trị nào của $p$ sẽ cho ta một số nguyên tố. Phải mất 300 năm và một số khám phá quan trọng trong toán học để giải quyết phỏng đoán của ông.
Và vào ngày 25/1/2013,tại ORLANDO, Florida, số nguyên tố Mersenne thứ 48 - lớn nhất cho tới giờ:
$2^{57,885,161}-1=581887266232246442......$
đã được phát hiện nhờ Đội tìm kiếm số nguyên tố lớn (GIMPS) trên máy tính của tình nguyện viên Curtis Cooper. Số nguyên tố mới có 17.425.170 chữ số. Với 360.000 máy tính, đạt mức cao nhất là 150 nghìn tỷ phép tính mỗi giây, GIMPS chạy 17 năm liên tục, và trở thành dự án chạy lâu nhất trong lịch sử Internet.
Để chứng minh không có lỗi trong quá trình phát hiện ra số nguyên tố, số nguyên tố mới được xác nhận độc lập bằng cách sử dụng các chương trình khác nhau chạy trên phần cứng khác nhau. Serge Batalov chạy phần mềm MLucas của Ernst Mayer trên một máy chủ trong 6 ngày để xác minh số nguyên tố mới. Jerry Hallett xác minh nguyên tố bằng cách sử dụng các phần mềm CUDALucas chạy trên một NVIDIA GPU trong 3,6 ngày. Cuối cùng, Tiến sĩ Jeff Gilchrist xác minh tìm thấy bằng cách sử dụng các phần mềm GIMPS trên một CPU Intel i7 trong 4,5 ngày và chương trình CUDALucas trên một NVIDIA GTX 560 Ti trong 7,7 ngày.
Phương pháp tốt nhất để kiểm tra tính nguyên tố của các số Mersenne được dựa vào sự tính toán một dãy tuần hoàn, được phát biểu đầu tiên bởi Lucas năm 1878 và chứng minh bởi Lehmer vào những năm 1930. Hiện nay nó được gọi là Cuộc kiểm tra Lucas-Lehmer với số Mersenne.
Tiến sĩ Cooper là một giáo sư tại trường Đại học Central Missouri. Đây là kỉ lục thứ ba cho Tiến sĩ Cooper và Đại học của ông. Đầu tiên kỉ lục của họ đã được đưa ra vào năm 2005, và bị phá vỡ bởi kỷ lục thứ hai của họ vào năm 2006. Máy vi tính tại UCLA đã phá vỡ kỷ lục trong năm 2008 với một số có 12.978.189 chữ số. UCLA nắm giữ kỉ lục cho đến khi Đại học Central Missouri phá vỡ kỷ lục thế giới với phát hiện này. Tiến sĩ Cooper và Đại học Central Missouri là những cá nhân có đóng góp lớn nhất cho dự án này. Phát hiện này được nhận giải thưởng GIMPS trị giá $ 3.000. Giải thưởng GIMPS tiếp theo sẽ được dành cho người tìm được số nguyên tố lớn với 100,000,000 chữ số, trị giá $150.000.
Ngoài ra, có một công thức nổi tiếng về việc tạo ra 1 số hoàn hảo từ 1 số nguyên tố Mersenne( số hoàn hảo là 1 số mà tổng các ước của nó bằng chính nó): $2^{p-1}(2^{p}-1)$ là số hoàn hảo. Số hoàn hảo mới được tìm ra là $2^{57,885,160}(2^{57,885,161}-1)$. Số này có tới hơn 34 triệu chữ số.
Nguồn: tại http://www.mersenne....us/57885161.htm
#392839 Giải thưởng Wolf năm 2013
 Đã gửi bởi
bachocdien
on 03-02-2013 - 16:29
trong
Tin tức - Vấn đề - Sự kiện
Đã gửi bởi
bachocdien
on 03-02-2013 - 16:29
trong
Tin tức - Vấn đề - Sự kiện


George Daniel Mostow (bên trái), Đại học Yale, và Michael Artin (bên phải), MIT, đã được chọn để nhận giải thưởng Wolf năm 2013. Cả hai sẽ chia sẻ giải thưởng 100.000 USD. Mostow được vinh danh vì những đóng góp cơ bản và tiên phong của ông cho hình học và lý thuyết nhóm Lie, đặc biệt là lý thuyết cứng nhắc mạnh. Artin được vinh danh vì những đóng góp cơ bản của ông trong hình học đại số. Đó là một trong số các thành tựu lớn nhất của toán học nửa cuối của thế kỷ 20, Lý thuyết cứng nhắc mạnh của Mostow đã tạo ra một sự kết nối sâu sắc giữa Topo và hình học, mở ra một cánh cửa để nghiên cứu nhiều lĩnh vực liên quan khác trong toán học. Mostow cũng có những đóng góp có ảnh hưởng trong nhóm Lie và các nhóm con rời rạc của chúng, đồng thời ông cũng có những nghiên cứu quan trọng (một phần nghiên cứu với P. Deligne) trên các ví dụ của mạng trong không gian compact hyperbolic hai và ba chiều.
Michael Artin là một trong những nhà hình học lớn nhất của thế kỷ 20, ông đã có nhiều công trình đáng ngạc nhiên và có chiều sâu trong nhiều lĩnh vực khó. Cùng với Alexander Grothendieck, Artin đã giới thiệu đối đồng đều étale, một trong những công cụ cốt yếu của hình học đại số hiện đại. Cùng với Barry Mazur, Artin áp dụng ý tưởng từ hình học đại số để nghiên cứu vi đồng phôi của các đa tạp compact. Công việc rất độc đáo trong lý thuyết biến dạng và trong đại số không giao hoán của Artin đã có một ảnh hưởng lâu dài.
Cả Artin và Mostow đều từng giữ chức vụ chủ tịch AMS, Artin trong những năm 1991-1992, Mostow trong thời gian 1987-1988. Artin nhận giải thưởng AMS Steele năm 2002 cho thành tựu trọn đời, và Mostow năm 1993 đã nhận giải thưởng AMS Steele cho sự đóng góp của ông trong nghiên cứu.
Nguồn: http://www.ams.org/news?news_id=1765
#389268 Dự định sưu tầm một số bài toán trên Mathlinks.ro
 Đã gửi bởi
bachocdien
on 23-01-2013 - 14:50
trong
Tin tức - Vấn đề - Sự kiện
Đã gửi bởi
bachocdien
on 23-01-2013 - 14:50
trong
Tin tức - Vấn đề - Sự kiện
#387405 Vòng 1 BMO 2013
 Đã gửi bởi
bachocdien
on 17-01-2013 - 15:15
trong
Thi HSG Quốc gia và Quốc tế
Đã gửi bởi
bachocdien
on 17-01-2013 - 15:15
trong
Thi HSG Quốc gia và Quốc tế
#387396 Vòng 1 BMO 2013
 Đã gửi bởi
bachocdien
on 17-01-2013 - 14:50
trong
Thi HSG Quốc gia và Quốc tế
Đã gửi bởi
bachocdien
on 17-01-2013 - 14:50
trong
Thi HSG Quốc gia và Quốc tế
Câu 2: Cho 2 đường tròn $S$ và $T$ tiếp xúc nhau tại $X$. Có 1 tiếp tuyến chung tiếp xúc $S$ tại $A$ và $T$ tại $B$( $A$ khác $B$). Kẻ đường kính $AP$ của $S$. CM: $B,X$ và $P$ thẳng hàng.
Câu 3:Giải hệ phương trình
$\left\{\begin{matrix} x^{2}-4y+7=0\\ y^{2}-6z+14=0\\ z^{2}-2x-7=0 \end{matrix}\right.$
Câu 4: Tìm tất cả các số nguyên dương $n$ sao cho $12n-119$ và $75n-539$ là những số chính phương
Câu 5: 1 tam giác có chiều dài các cạnh tương ứng lớn nhất có thể là 2,3 và 4. Tính diện tích khả dĩ lớn nhất của tam giác.
Câu 6: Cho tam giác $ABC$. Cho đường tròn $S$ đi qua $B$ và tiếp xúc với $CA$ tại $A$, đường tròn $T$ đi qua $C$ và tiếp xúc với $AB$ tại $A$. Đường tròn $S$ và $T$ cắt nhau tại $A$ và $D$. $AD$ cắt đường tròn ngoại tiếp $ABC$ tại $E$, Chứng minh: $D$ là trung điểm $AE$.
#387138 Đề thi olympic toán Trung quốc 2013
 Đã gửi bởi
bachocdien
on 16-01-2013 - 13:43
trong
Thi HSG Quốc gia và Quốc tế
Đã gửi bởi
bachocdien
on 16-01-2013 - 13:43
trong
Thi HSG Quốc gia và Quốc tế
- Chứng minh $l_{1}$,$l_{2}$ có 1 điểm chung $P$
- Chứng minh $CA$, $AP$ và $PE$ có độ dài của 3 cạnh 1 tam giác vuông
Câu 3: Tìm tất cả các số thực dương $t$ thỏa mãn: tồn tai 1 tập $X$ thực vô hạn sao cho:
$max\left \{ \mid x-(a-d)\mid ,\mid y-a\mid,\mid z-(a+d)\mid\right \}> td$,$\forall x,y,z\in X$, $a,d\in R,d> 0$
Câu 4: Cho $n\geq 2$, có 1 tập hữu hạn $A_{1}, A_{2},...,A_{n}$ sao cho với $i,j\in \left \{ 1,2,...,n \right \},\left | A_{i}\Delta A_{j} \right |=\left | i-j \right |$. Tìm giá trị nhỏ nhất của $\sum_{i=1}^{n}\left | A_{i} \right |$
Câu 5: Cho số nguyên dương $n,0\leq i\leq n$ biểu diễn $ C_n^i\equiv c(n,i)(\bmod 2) $, ở đây $c(n,i)\in\left \{ 0,1 \right \}$, $f\left ( n,q \right )=\sum_{i=0}^{n}c\left ( n,i \right )q^{i}$. $m,n,q$ nguyên dương và $q+1\neq 2^{\alpha }$,$\forall \alpha\in N$.Chứng minh: $f(m,q)\mid f(n,q)$ thì $f(m,r)\mid f(n,r)$ với r nguyên dương.
Câu 6: $m,n$ là các số nguyên dương, tìm số nguyên dương $N$ nhỏ nhất thỏa mãn: nếu S là 1 tập các số nguyên dương chứa 1 hệ thặng dư đầy đủ mod $m$ và $\left | S \right |=N$ thì tồn tại 1 tập không rỗng $A\subseteq S$ mà $n\mid \sum_{x\in A}x$
#386723 Đề thi Olympic toán sinh viên ĐH Ngoại Thương TPHCM 2013
 Đã gửi bởi
bachocdien
on 14-01-2013 - 19:33
trong
Thảo luận về các kì thi, các kì kiểm tra Toán sinh viên
Đã gửi bởi
bachocdien
on 14-01-2013 - 19:33
trong
Thảo luận về các kì thi, các kì kiểm tra Toán sinh viên
lúc em làm, chéo hóa...saiCâu này lừa tình quá @@
Chéo hóa ma trận $A$
$$A=P \begin{bmatrix}2 & 0 &0 \\0 &-1 &0 \\ 0& 0 &1\end{bmatrix} P^{-1}$$
Với $P=\begin{bmatrix}1 & -1 &1 \\2 &-3 &1 \\ 1& 1 &1\end{bmatrix} $
$P^{-1}=\begin{bmatrix}-2 & 1 &1 \\-\frac{1}{2} &0 &\frac{1}{2} \\ \frac{5}{2}& -1 &\frac{-1}{2}\end{bmatrix}$
Suy ra $$\dfrac{1}{k}A^k=\frac{1}{k} \begin{bmatrix}
-2.2^k+\frac{1}{2}(-1)^k+\frac{5}{2} & 2^k-1 &2^k-\frac{1}{2}(-1)^k-\frac{1}{2} \\
-4.2^k+\frac{3}{2}(-1)^k+\frac{5}{2} &2.2^k-1 &2.2^k-\frac{3}{2}(-1)^k-\frac{1}{2} \\
-2.2^k-\frac{1}{2}(-1)^k+\frac{5}{2}& 2^k-1 &2^k+\frac{1}{2}(-1)^k-\frac{1}{2}
\end{bmatrix}$$
Lấy một phần tử chẳng hạn $\dfrac{2^k-1}{k}\underset{k \to +\infty}{\longrightarrow} +\infty$
Do đó $\sum_{k=1}^n \frac{1}{k}A^k $ không hội tụ khi $n \to +\infty $ , suy ra $U_n$ không hội tụ khi $n \to +\infty$
#385560 Đề thi Olympic toán sinh viên ĐH Ngoại Thương TPHCM 2013
 Đã gửi bởi
bachocdien
on 11-01-2013 - 12:41
trong
Thảo luận về các kì thi, các kì kiểm tra Toán sinh viên
Đã gửi bởi
bachocdien
on 11-01-2013 - 12:41
trong
Thảo luận về các kì thi, các kì kiểm tra Toán sinh viên
Câu 1. Cho ma trận $A=\begin{pmatrix} -2 & 1 & 2\\ -7 & 3 & 5\\ -1 & 1 & 1 \end{pmatrix}$. đặt $U_{n}=E+\sum_{k=1}^{n}\frac{1}{k}A^{k}$ với E là ma trận đơn vị cấp 3. Tính $\lim_{n \to \infty }U_{n}$
Câu 2. Dãy số Fibonaci được định nghĩa bởi $F_{0}=1$;$F_{1}=1$;$F_{n+1}=F_{n}+F_{n-1}$nếu $n\geq 1$
a)CMR: $F_{n}^{2}-F_{n-1}F_{n+1}=(-1)^{n}$ nếu $n\geq 1$
b)Tính giá trị của $\prod_{n=1}^{+\infty }\left ( 1+\frac{(-1)^{n+1}}{F_{n}^{2}} \right )$
Câu 3. Với $a_{i},b_{i}(i=1,2,...n)$ là các số thực cho trước đôi một phân biệt. Xét hệ phương trình sau:
$$\left\{\begin{matrix} \frac{x_{1}}{a_{1}-b_{1}}+\frac{x_{2}}{a_{1}-b_{2}}+...\frac{x_{n}}{a_{1}-b_{n}}=1\\ \frac{x_{1}}{a_{2}-b_{1}}+\frac{x_{2}}{a_{2}-b_{2}}+...+\frac{x_{n}}{a_{2}-b_{n}}=1\\ .......................................\\ \frac{x_{1}}{a_{n}-b_{1}}+\frac{x_{2}}{a_{n}-b_{2}}+...+\frac{x_{n}}{a_{n}-b_{n}}=1 \end{matrix}\right.$$
a)Giải hệ phương trình
b)Tính tổng các ngiệm
Câu 4. Cho $A=\begin{bmatrix} a &b \\ c &d \end{bmatrix}$ là một ma trận thực hoặc phức với các giá trị riêng phân biệt $\lambda _{1},\lambda _{2}$ và các vector riêng tương ứng $X_{1},X_{2}$. Cho $P=\begin{bmatrix} X_{1}\setminus X_{2} \end{bmatrix}$. CMR hệ $\left\{\begin{matrix} x_{n+1}=ax_{n}+by_{n}\\ y_{n+1}=cx_{n}+dy_{n} \end{matrix}\right.$ có nghiệm là $\begin{bmatrix} x_{n}\\ y_{n} \end{bmatrix}=\alpha \lambda _{1}^{n}X_{1}+\beta \lambda _{2}^{n}X_{2}$ trong đó $\alpha ,\beta$ được xác định bởi phương trình $\begin{bmatrix} \alpha \\ \beta \end{bmatrix}=P^{-1}\begin{bmatrix} x_{0}\\ y_{0} \end{bmatrix}$
Câu 5. Cho ma trận $A=\begin{bmatrix} 2 &-1 &0 &0 \\ 0 &2 &-1 &0 \\ 0 &0 &2 &-1 \\ 0 &0 &0 &2 \end{bmatrix}$. tìm tất cả các ma trận X thỏa mãn $A.X=X.A$
câu 6.Biện luận theo m nghiệm đa thức $P(x)$ của phương trình hàm sau: $1+x+P(x)=m[P(x+1)+P(x-1)]$
#384495 2013-NĂM THỐNG KÊ QUỐC TẾ
 Đã gửi bởi
bachocdien
on 07-01-2013 - 21:14
trong
Tin tức - Vấn đề - Sự kiện
Đã gửi bởi
bachocdien
on 07-01-2013 - 21:14
trong
Tin tức - Vấn đề - Sự kiện
Mục đích của Statistics2013 là nâng cao tầm quan trọng của thống kê tới cộng đồng khoa học quốc tế, thương nhân và người dùng dữ liệu thuộc chính phủ, người làm chính trị và truyền thông đa phương tiện, công nhân, sinh viên và toàn thể quần chúng nói chung. Mục đích của nó cũng bao gồm việc thúc đẩy , phát triển thống kê như 1 ngành nghề, đặc biệt là trong giới trẻ. Một danh sách đang ngày càng tăng của các tổ chức đang tham gia trong Năm Quốc tế về Thống kê. Tuần trước, số lượng các nước tham gia đã đạt 105, với hơn 1.350 tổ chức tham gia.
Cựu chủ tịch của RSS( Royal Statistics Society- Hội Thống Kê Hoàng Gia), Denise Lievesley, là đại diện cho Hội Năm Quốc tế Thống Kê sẽ chỉ đạo ủy ban, cùng với thành viên: Rob Mastrodomenico. RSS quảng bá Statistics2013 thông qua chiến dịch getstats, tạp chí Significance và các sự kiện thường xuyên được chạy suốt năm, bao gồm các cuộc họp thường xuyên của RSS, bài giảng của Cathie Marsh trong tháng mười một và tất nhiên, là hội nghị hàng năm của RSS, năm nay sẽ diễn ra tại Newcastle vào tháng Chín. RSS cũng sẽ tổ chức một sự kiện quốc tế tại RSS, đường Errol trong mùa thu để chào mừng Statistics2013.
Ban Tổ chức hoan nghênh tất cả các bên quan tâm tham gia trong Statistics2013. Và Ban tổ chức cũng khuyến khích sự phân bố rộng rãi của URL Statistics2013.org
Gần đây Statistics2013 cũng phát hành một video để kỷ niệm sự ra mắt:
#382271 Năm 2013 là năm toán học trái đất (MPE2013)
 Đã gửi bởi
bachocdien
on 31-12-2012 - 15:44
trong
Tin tức - Vấn đề - Sự kiện
Đã gửi bởi
bachocdien
on 31-12-2012 - 15:44
trong
Tin tức - Vấn đề - Sự kiện
Hành tinh của chúng ta được thiết lập cho các quá trình vận động của tất cả mọi thứ, bao gồm các quá trình địa vật lý trong lớp vỏ trái đất, các lục địa và các đại dương, các chu trình của không khí xác định thời tiết và khí hậu của chúng ta, những chu trình sinh học liên quan đến các sinh vật sống và tương tác giữa chúng, và những hoạt động của loài người trong những lĩnh vực tài chính, nông nghiệp, nước, giao thông, và năng lượng. Những thách thức mà hành tinh và nền văn minh của chúng ta đang phải đối mặt là rất đa dạng, và toán học đóng vai trò trung tâm trong việc tìm hiểu và đối phó với những thử thách này.
Nhiệm vụ của Dự án MPE là:
- Khuyến khích nghiên cứu trong việc xác định và giải đáp những câu hỏi cơ bản về hành tinh của chúng ta
- Khuyến khích những nhà giáo dục ở tất cả các cấp để tuyên truyền những vấn đề liên quan đến trái đất
- Thông báo cho công chúng về những vai trò thiết yếu của khoa học toán học trong việc đối mặt với những thách thức đến với trái đất
MPE 2013 được ra đời từ ý muốn của cộng đồng toán học quốc tế để tìm hiểu nhiều hơn về những thách thức mà hành tinh của chúng ta đang phải đối mặt và những vấn đề toán học cơ bản, đồng thời gia tăng các hoạt động ngiên cứu về những vấn đề này. Thật vậy, những khuynh hướng gần đây đã gia tăng áp lực để hiểu được hành tinh của chúng ta và môi trường của nó: gia tăng dân số, cạnh tranh vì những nguồn tài nguyên, tăng tần số và cường đồ những hiện tượng khí tượng đặc biệt, và những bằng chứng chỉ ra sự biến đổi khí hậu trong 1 thời gian dài. Những nhà toán học có một hiểu biết sâu sắc trong việc mô hình hóa và tìm ra các giải pháp cho các vấn đề. MPE 2013 tạo ra những cơ hội đặc biệt cho các quan hệ đối tác lâu dài, cả trong khoa học toán học lẫn trong các ngành khoa học khác. Nó sẽ cho phép đào tạo một thế hệ mới các nhà nghiên cứu làm việc trong những vấn đề khoa học liên quan đến thay đổi khí hậu và phát triển bền vững.
Song song với các bộ phận của khoa học, bộ phận tiếp cận cộng đồng của MPE 2013 minh họa cho cộng đồng và cho nhà trường những quy luật của khoa học toán học giúp giải quyết một số vấn đề cấp bách nhất thế giới. nó sẽ cho phép khuyến khích những đứa trẻ ở trường bằng việc cung cấp những câu trả lời kích thích cho câu hỏi giống như kiểu: ”Toán học hữu ích cho cái gì”.
Chủ đề “Toán học của hành tinh Trái Đất” được hiểu một cách rộng nhất có thể. Ngoài sự biến đổi khí hậu và phát triển bền vững, nó bao gồm địa lý, sinh thái, và dịch tễ học , sự đa dạng sinh học, cũng như những tổ chức toàn cầu về trái đất của con người. Những chủ đề khác nhau có thể được phân loại thành 4 chủ đề
Bốn chủ đề của MPE 2013:
- Một hành tinh đề khám phá: biển; khí tượng học và khí hậu; các quá trình che phủ; tài nguyên thiên nhiên, hệ mặt trời
- Một hành tinh cung cấp sự sống: sinh thái, sự đa dạng sinh học, tiến hóa
- Một hành tinh được tổ chức bởi loài người: hệ thống chính trị, kinh tế, và tài chính, tổ chức mạng lưới giao thông vận tải, quản lý các nguồn tài nguyên năng lượng
- Một hành tinh đang gặp nguy hiểm: biến đổi khí hậu, sự phát triển bền vững, dịch bệnh; các loại xâm lấn; thiên tai.
Nguồn: http://mpe2013.org/about-mpe2013/
#381729 Chứng minh $ (A')^{*}=(A^{*})^{'}...
 Đã gửi bởi
bachocdien
on 29-12-2012 - 21:19
trong
Đại số tuyến tính, Hình học giải tích
Đã gửi bởi
bachocdien
on 29-12-2012 - 21:19
trong
Đại số tuyến tính, Hình học giải tích
$\Rightarrow A^{2}=\begin{pmatrix} a^{2}+bc & ab+bd\\ ca+dc & cb+d^{2} \end{pmatrix}$
$A^{2}=0$
$\Rightarrow \left\{\begin{matrix} a^{2}=-bc & \\ a=-d & \end{matrix}\right.$
=> ma trận A cần tìm có detA=0 và $A=\begin{pmatrix} a & b\\ c & -a \end{pmatrix}$
2. A' với A* là gì vậy
#380470 Logic trong các bài kiểm tra thuốc
 Đã gửi bởi
bachocdien
on 25-12-2012 - 21:49
trong
Toán học lý thú
Đã gửi bởi
bachocdien
on 25-12-2012 - 21:49
trong
Toán học lý thú

làm thế nào để biết 1 vận động viên
có thực sự gian lận?
Để tìm hiểu xem liệu một vận động viên có thể tìm được một lợi thế không công bằng bằng cách sử dụng thuốc hay không? Nhiều cuộc kiểm nghiệm đã được tiến hành. Chi tiết các cuộc kiểm tra đó phụ thuộc vào những chất bị cấm đang bị điều tra, nhưng logic phía sau những cuộc kiểm tra như vậy là giống nhau: một số đo lường được thực hiện và nếu giá trị của chúng vượt qua một ngưỡng thì điều này được xem là bằng chứng đầy đủ cho sự gian lận.
Làm thế nào để biết rằng 1 vận động viên không vượt qua bài kiểm tra về thuốc có thực sự gian lận, và những lời buộc tội có đáng tin cậy? Trong ngôn ngữ của xác suất, chúng ta tìm xác suất có điều kiện để vận động viên phạm tội vì họ không qua được bài kiểm tra Doping, kí hiệu là: Pr(có tội | thất bại). Cần có 3 con số để làm việc này. Thứ nhất là độ nhạy của cuộc kiểm tra: tỉ lệ người sử dụng thuốc không vượt qua được bài kiểm tra. Về mặt xác suất, đây là xác suất có điều kiện mà một người có tội ( sử dụng thuốc) đồng thời không vượt qua được bài kiểm tra, ta kí hiệu là: Pr(thất bại | có tội). Chúng ta hy vọng con số này là gần tới 100%. Con số thứ 2 là đặc tính của cuộc kiểm tra: tỷ lệ những người không sử dụng đồng thời vượt qua bài kiểm tra. Lại một lần nữa, con số này nên gần tới 100%, có nghĩa là Pr(thất bại | vô tội) nên gần đến 0. Số cuối cùng là tỷ lệ thực tế của người dùng thuốc trong số đông có liên quan, số đông đó là nhóm vận động viên có thể đã được kiểm tra. Rất khó để biết chính xác, nhưng chúng ta có thể ước tính 1 cách hợp.
Nếu chúng ta có 3 con số đó ta có thể sử dụng một kết quả toán học gọi là : lý thuyết của Bayes, cái mà có thể cho chúng ta câu trả lời. Lý thuyết đó chỉ ra rằng ta có thể làm việc dễ dàng hơn với tỷ lệ xác suất thay vì xác suất. Nhắc lại rằng: nếu xác suất 1 sự kiện xuất hiện là 80%, xác suất nó không xảy ra là 20%, vì vậy tỷ lệ xác suất là 80/20, hoặc 4/1; nếu thay đổi thành 90% thì tỷ lệ xác suất là 90/10, hoặc 9/1. Xác suất xác định tỷ lệ này và ngược lại.
Trước những bằng chứng về sử dụng thuốc đã được tìm thấy, xác suất xảy ra sự kiện”1 vận động viên được chọn ngẫu nhiên là 1 người gian lận” chỉ là tỷ lệ của những người gian lận trong số những người còn lại. Vì vậy ta sử dụng hình minh họa này để tìm ra giá trị tương ứng cho tỉ số xác suất này. Tỷ số này:
tỷ lệ những người gian lận/ tỷ lệ những người vô tội
Là tỷ số xác suất tiên nghiệm của những người phạm tội
Giả sử 1 vận động viên không vượt qua được bài kiểm tra. Chúng ta nên tìm tỷ số xác suất xác suất hậu nghiệm của những người sử dụng thuốc như thế nào? Đầu tiên tính sức nặng của bằng chứng (ảnh hưởng của bằng chứng đối với mức độ tin cậy), tức là xác định tỉ số
Pr( thất bại/có tội)/Pr( thất bại/vô tội)
bằng cách sử dụng độ nhảy và đặc trưng của cuộc kiểm tra nói trên. Bây giờ lý thuyết của Bayes sẽ nói cho ta biết câu trả lời ta đang tìm kiếm, tỷ lệ xác suất hậu nghiệm, chỉ đơn giản là nhân tỷ lệ xác suất tiên nghiệm với sức nặng của bằng chứng. Bạn có thể chuyển nó thành 1 giá trị xác suất nếu bạn muốn.
Những con số thường dễ hình dung hơn. Giả sử tỷ lệ gian lận là 1%, độ nhạy là 95%, và đặc trưng của bài kiểm tra cũng là 95%. Tỷ số xác suất trước là 1/99. Sức nặng của các bằng chứng là 95/5.( Bạn có đồng ý không? Hãy cẩn thận với định nghĩa của nó), vậy tỷ lệ xác suất hậu nghiệm của những người phạm tội là
$\frac{1}{99}\times \frac{95}{5}=\frac{19}{99}$
khoảng 0.19. Để chuyển từ tỷ lệ xác suất sang giá trị xác suất, chúng ta chia tỷ lệ này cho 1 cộng với chính nó:
$\frac{\frac{19}{99}}{1+\frac{19}{99}}=0.16$
Vậy ta có 1 xác suất khoảng 16%, xác suất này có lẽ sẽ gây thất vọng cho nhiều người. Mặc dù bài kiểm tra chỉ sai 5 lần trong số 100 trường hợp cả người có tội cũng như người vô tội nhưng nó vẫn là không đủ tốt. Vậy ta có thể đuổi một vài người ra khỏi Olympic chỉ với xác suất 16% là họ gian lận không?
Dù ban đầu cả độ nhạy và đăc trưng của cuộc kiểm tra đều đạt 95%, nhưng có thể thấy kết quả không được như yêu cầu. Hãy tưởng tượng có 10,000 người và 1% sử dụng thuốc. Nghĩa là có 9900 người trong sạch, và 100 người gian lận. chúng ta kỳ vọng rằng bài kiểm tra sẽ tìm được 95% những người gian lận, nhưng nó cũng sẽ chạm được tới 5% những người vô tội, tức 495 người khác. Vì vậy trong 590 vận động viên thất bại trong bài kiểm tra chỉ có 95 người trong số họ, 16%, là gian lận.
Chúng ta không thể kỳ vọng những bài kiểm tra có độ nhạy 100% hay độ đặc trưng 100%, sai sót sẽ xảy ra. Một cơ quan có thẩm quyền phải đặt lại ngưỡng để tạo thành 1 sự cân bằng có thể chấp nhận được giữa những sai lầm của các cáo buộc 1 vận động viên vô tội là có tội, và những sai lầm trong việc để những người sử dụng thuốc nhưng vượt qua bài kiểm tra là trong sạch.
#379766 Ảnh Fractal
 Đã gửi bởi
bachocdien
on 23-12-2012 - 10:29
trong
Toán học lý thú
Đã gửi bởi
bachocdien
on 23-12-2012 - 10:29
trong
Toán học lý thú
Tập Mandelbrot

Kết quả mới này được chứng minh bởi Kathyn A.Lindsey và sau đó là William P.Thurston, áp dụng đối với những hình có đường viền được tạo bởi một tập hữu hạn những đường cong đóng đơn. Đây là những vòng lặp liên tục trong mặt phẳng mà không tự giao với chính nó. Các hình Fractal (từ những hình 2D) được tạo ra từ việc nhìn những điểm trong mặt phẳng, những điểm di chuyển xung quanh 1 phân lớp của hàm số
Để hiểu được công việc này diễn ra như thế nào, hãy xét 1 hàm số bậc 2
$$f(x)=x^2$$
Khi bạn thay $x=0$ vào hàm số, kết quả là:
$$f(0)=0^2=0$$
Lại là 0, vì vậy 0 được gọi là điểm cố định. Điều tương tự xảy ra với $x=1$
$$f(1)=1^2=1$$
Tuy nhiên các giá trị khác của x còn thú vị hơn. Lấy $x=2$ làm ví dụ. ta có:
$$f(2)=4$$
Nếu tiếp tục sử dụng 4 làm giá trị của $x$ ta có:
$$f(4)=4^2=16$$
Sử dụng 16 làm giá trị mới:
$$f(16)=16^2=256$$

Bạn có thể thấy chuyện gì xảy ra nếu ta lặp lại quy trình này, sử dụng kết quả trước làm giá trị của $x$ trong lần tính sau: những con số càng ngày càng lớn hơn. Và thực tế bạn có thể làm những con số này lớn 1 cách tùy ý bằng cách lặp đi lặp lại quá trình này. Chuỗi các con số mà bạn nhận được theo cách này, bắt đầu từ 2, được gọi là quỹ đạo của 2 theo hàm $f$, và ta nói rằng quỹ đạo của 2 thoát ra đến vô cùng. Những hàm của những số lớn hơn 1 và nhỏ hơn -1 đều có quỹ đạo thoát ra đến vô cùng.
Nhưng chuyện gì xảy ra với những con số nằm trong khoảng -1 đến 1? Bình phương của một số lớn hơn 0 nhỏ hơn 1 luôn cho ta một số dương nhỏ hơn 1, vì thế những số này không có quỹ đạo thoát ra vô cùng( vì các giá trị càng ngày càng nhỏ). Ví dụ: $x=\frac{-1}{2}$
$$f(\frac{-1}{2})=\frac{1}{4}$$
$$f(\frac{1}{4})=\frac{1}{16}$$
$$f(\frac{1}{16})=\frac{1}{256}$$
Như vậy, trong khi ta thiết lập được quỹ đạo cho các số $x>1$ tiến đến vô cùng thì quỹ đạo của những số $ -1 < x<1$
Bạn cũng có thể sử dụng một hàm tương tự khác, ví dụ:
$$f(x)=x^{15}-3x^7+9x+5$$
$$f(x)=x^5+x^4+x^3+x^2+x+1$$
hoặc
$$f(x)=x^{100}+2x^{51}+7$$
Những hàm này gọi là những đa thức và có dạng tổng quát là:
$$f(x)=a_{n}x^{n}+a_{n-1}x^{n-1}+...+a_{1}x+a_{0}$$
ở đây $a_{0},a_{1},...,a_{n}$ là các hằng số.
Với những hàm số trên sẽ có 1 cách chọn điểm có quỹ đạo thoát và 1 cách chọn những điểm có quỹ đạo bị bẫy trong 1 khoảng xác định
Với những hàm số trên sẽ có 1 cách chọn điểm có quỹ đạo thoát và 1 cách chọn những điểm có quỹ đạo bị bẫy trong 1 khoảng xác định.Với những hàm số trên sẽ có 1 cách chọn điểm có quỹ đạo thoát và 1 cách chọn những điểm có quỹ đạo bị bẫy trong 1 khoảng xác định. Với những hàm số trên sẽ có 1 cách chọn điểm có quỹ đạo thoát và 1 cách chọn những điểm có quỹ đạo bị bẫy trong 1 khoảng xác định. Nhưng tất cả những điều này thì có liên hệ gì với những hình trong mặt phẳng? Trong ví dụ trên, các hàm đa thức được áp dụng cho những điểm nằm trên trục số( mỗi giá trị của $x$ tương ứng với 1 điểm)
Nhưng có 1 cách biến chúng thành những hàm áp dụng cho các điểm trên mặt phẳng, những hàm đưa tất cả các điểm riêng lẻ $(x,y)$ đến những điểm khác $(z,w)$ trong mặt phẳng. Để làm được điều này bạn cần sử dụng số phức.( cho $x$ có giá trị phức và biểu diễn các điểm trên mặt phẳng phức)
Chỉ cần như trước với trục số, một hàm f bây giờ cho 1 phần mặt phẳng vào những quỹ đạo thoát hoặc bị giam. Tập hợp những điểm có quỹ đạo bị bẫy gọi là 1 tập Julia đóng. Và ranh giới của một tập Julia đóng( mép của nó) được gọi đơn giản là tập Julia.
Vùng màu đen là tập Julia đóng của đa thức bậc hai. Viền ngoài của nó là tập Julia

Nói chung tập Julia của các đa thức là những hình Fractals: những hình có chu vi vô hạn và cũng rất phức tạp( hình tự đồng dạng)
Kết quả mới nói rằng, bất kì đường cong đóng đơn nào trên mặt phẳng cũng có thể lấy gần đúng là 1 tập Julia của đa thức -bạn có thể nối những đường cong bằng tập Julia- và như vậy một sự xấp xỉ có thể được thực hiện chính xác như bạn muốn. Nếu bạn cố gắng lấy gần đúng 1 tập hợp những đường cong đóng đơn, bạn cần sử dụng những hàm số hơi phức tạp hơn. Chúng được gọi là những hàm số hợp lý nhận được khi thực hiện chia một đa thức cho 1 đa thức khác. Tập những đường cong sau đó được lấy gần đúng là 1 phần của tập Julia của những đa thức này.

Tập Julia của hình ảnh con mèo
Và sự kết nối đến tập hợp Mandelbrot là gì? Nó chỉ ra rằng các điểm trên mặt phẳng có thể được sử dụng để gắn những đa thức bậc hai: mỗi đa thức bậc hai có thể được liên kết với một điểm trên mặt phẳng. Những điểm thuộc về tập hợp Mandelbrot, có màu đen trong hình trên, tương ứng với tập Julia bao gồm 1 thành phần, chứ không phải là một tập hợp những phần riêng biệt. tập hợp Mandelbrot và hình Fractal của nó khá phổ quát. Nó không chỉ đưa ra kết nối với đa thức bậc hai mà còn với những lớp khác của hàm số.
#374623 Bài 1:Cho $A$ là ma trận vuông thỏa mãn $A^3 =0$.Tính...
 Đã gửi bởi
bachocdien
on 02-12-2012 - 19:53
trong
Đại số tuyến tính, Hình học giải tích
Đã gửi bởi
bachocdien
on 02-12-2012 - 19:53
trong
Đại số tuyến tính, Hình học giải tích
=>E=0 vô lý
=> A không kha nghịch
Vì I là ma trận đơn vị. suy ra áp dụng khai triển nhị thức Niu tơn:
$$(I+A)^{2010}=\sum_{k=0}^{2010}C_{2010}^{k}\textrm{} A^{k}I^{2010-k}$$
$$(I+A)^{2010}=A+ C_{2010}^{2}\textrm{} A^{2}+ I (vì A^{3}=0)$$
Bài 2: từ $A^{2}=A$=> $A^{n}= A^{n-1}=A$
Áp dụng khai triển tương tự như trên:
$VT= A\sum_{k=0}^{2010}C_{2010}^{k}\textrm{}$
$VT= (2^{n}-1)A+E$
............................................
@vo van duc: Đầu dòng viết hoa nhé mấy em!
- Diễn đàn Toán học
- → bachocdien nội dung


