Vừa rồi kết quả VMO khá khả quan với một số thành viên của diễn đàn, mình xin gửi lời chúc mừng tới các bạn. Để đầy mạnh phong trào đồng thời cũng có ý nghĩa cho việc chuẩn bị vòng 2, mình xin mạn phép đầy nhanh tốc độ Marathon bằng cách đề nghị song song thêm 2-3 bài toán, ai giải xong bài nào cứ tiếp tục đề nghị số thứ tự tiếp tục, làm thế để tăng số lượng bài và tăng hiệu suất làm việc, mong các bạn khi giải xong đề nghị các bài toán mới sát với vòng 2 để chúng ta cùng ôn tập luôn. Chúng ta vẫn duy trì quy tắc sau 2 ngày nếu chưa ai giải thì người đề nghị post đáp án !

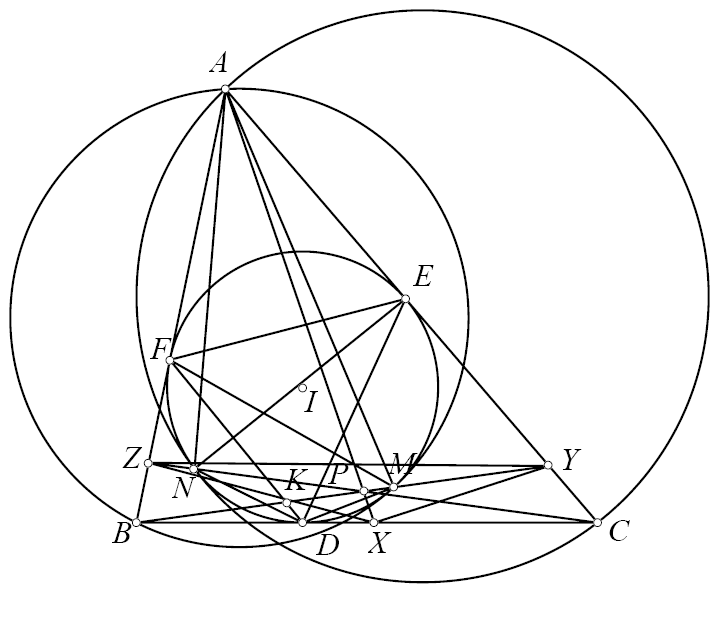
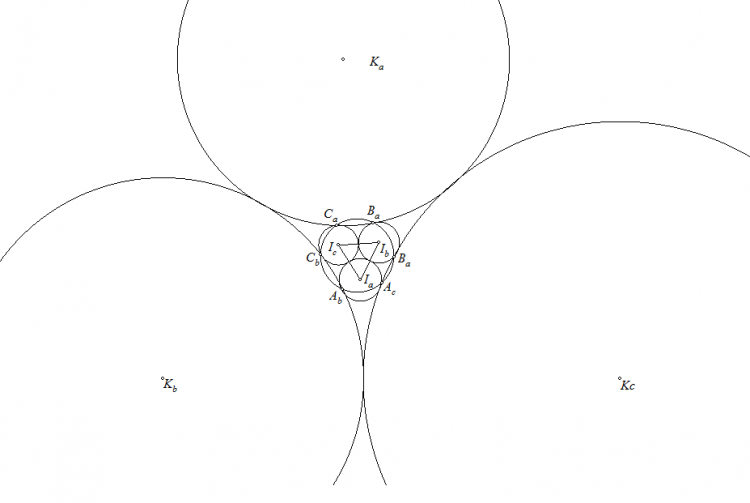
Bài toán 143 (Tập huấn IMO 2013). Cho tam giác $ABC$ nội tiếp đường tròn $(O)$. $P$ là điểm bất kỳ. Đường thẳng qua $P$ vuông góc với $BC$ cắt $CA,AB$ tại $A_1,A_2$. Gọi $(K_a)$ là đường tròn ngoại tiếp tam giác $AA_1A_2$. Tương tự có $(K_b),(K_c)$. Gọi $(K)$ là đường tròn tiếp xúc trong với $(K_a),(K_b),(K_c)$. Gọi $(L)$ là đường tròn tiếp xúc ngoài với $(K_a),(K_b),(K_c)$. Chứng minh rằng các đường tròn $(O),(K),(L)$ đồng trục.

Bài toán gốc đã có và được giải ở đây từ năm 2013.

Đúng vậy, cám ơn Bảo dẫn lại link, xin dịch lại lời giải của Telv Cohl như sau

Giải bài toán 141 (Telv Cohl). Gọi $ V_{ij} $ ($ i, $ $ j $ $ \in $ $ \mathbb{N}, $ $ 1 $ $ \leq $ $ i $ $ < $ $ j $ $ \leq $ $ 4 $) lần lượt là giao điểm của $ \ell_i, $ $ \ell_j $ và gọi $ T $ là hình chiếu của $ V_{23} $ trên $ \ell_4. $ Ta biết rằng $ H_k, $ $ P_k $ ($ k $ $ \in $ $ \mathbb{N}, $ $ 1 $ $ \leq $ $ k $ $ \leq $ $ 4 $) nằm trên đường thẳng Steiner của tứ giác toàn phần tạo bởi $ \ell_1, $ $ \ell_2, $ $ \ell_3, $ $ \ell_4, $ và chú ý rằng $ T $ $ \in $ $ \odot (H_1P_4X_4) $ nên ta thu được (từ định lý Reim's) $ H_1, $ $ H_2, $ $ V_{34} $ $ X_4 $ Đồng viên. Tương tự ta có thể chứng minh $ X_3 $ nằm trên đường tròn này và $ H_1, $ $ H_3, $ $ V_{24}, $ $ X_2, $ $ X_4 $ cũng đồng viên, do đó ta thu được

$$ \measuredangle X_2X_4X_3 = \measuredangle X_2X_4H_1 + \measuredangle H_1X_4X_3 = \measuredangle X_2V_{24}H_1 + \measuredangle H_1V_{34}X_3 = \measuredangle (\ell_2, \perp \ell_3) + \measuredangle (\perp \ell_2, \ell_3). $$

Tương tự, ta có $ \measuredangle X_2X_1X_3 $ $ = $ $ \measuredangle (\ell_2, \perp \ell_3) $ $ + $ $ \measuredangle (\perp \ell_2, \ell_3), $ do đó chúng ta thấy rằng $ X_1, $ $ X_2, $ $ X_3, $ $ X_4 $ đồng viên.

Mình xin đề nghị bài tiếp cho topic tiếp tục.

Bài toán 142. Cho hình chữ nhật $ABCD$ và $P$ nằm trên cạnh $AB$. $Q,R$ đối xứng với $A,B$ qua $P$. Trung trực $PC,PD$ lần lượt cắt $BC,AD$ tại $M,N$. $MQ$ cắt $NR$ tại $X$. Chứng minh rằng đường tròn $(X,XP)$ tiếp xúc $CD$.

Cám ơn Tuấn, xin trích dẫn lại lời giải của Telv ở #4 trong đây.

Giải bài toán 140 (Telv Cohl). Lấy điểm $Y$ sao cho hai tam giác $YBA$ và $XCD$ đồng dạng cùng hướng. Khi đó $\angle YAX+\angle YBX=\angle YAB+\angle BAX+\angle YBA+\angle ABX=\angle BAX+\angle XDC+\angle BAX+\angle XCD=180^\circ$. Từ đó $AYBX$ nội tiếp. Lại có $\angle YAB=\angle XDC=\angle XBA$ nên $AY\parallel BX$ do đó $AYBX$ là hình thang cân. Suy ra $AB^2=BY.AX+AY.BX$, lại có $YBA$ và $XCD$ đồng dạng nên $AB.CD=XA.XC+XB.XD$. Chứng minh tương tự $AD.BC=XA.XC+XB.XD$ nên $AB.CD=AD.BC$. Kết thúc chứng minh.

Bài toán 141. Cho bốn đường thẳng $\ell_1,\ell_2,\ell_3,\ell_4$ bất kỳ trong mặt phẳng. Gọi $H_1$ là trực tâm tam giác tạo bởi các đường thẳng $(\ell_2,\ell_3,\ell_4)$. $P_1$ là cực trực giao của $\ell_1$ với tam giác tạo bởi các đường thẳng $(\ell_2,\ell_3,\ell_4)$. $X_1$ thuộc $\ell_1$ sao cho $P_1X_1\perp P_1H_1$. Định nghĩa tương tự các điểm $X_2,X_3,X_4$. Chứng minh rằng $X_1,X_2,X_3,X_4$ đồng viên.

Bài toán 13 (Tập huấn tuyển Hàn Quốc 2017). Cho tam giác $ABC$ có tâm bàng tiếp góc $A,B,C$ là $J,K,L$. $D,E,F$ đối xứng với $A,B,C$ lần lượt qua $BC,CA,AB$.

a) Chứng minh rằng $JD,KE,LF$ đồng quy tại $P$.

b) Gọi $X,Y,Z$ đối xứng $P$ qua $BC,CA,AB$. Chứng minh rằng $AX,BY,CZ$ đồng quy.

Xin lỗi vì lúc nãy mình xem lướt quá không đọc rõ. Mình xin nói lại thế này thế này, việc các thành viên đóng góp lời giải nói chung là rất đáng trân trọng. Còn việc nói ý tưởng hay không thì điều đó khong mấy quan trọng vì việc giải được một bài toán xuất phát từ một quá trình học tập lâu dài và đúc rút nhiều kinh nghiệm giải. Ai cũng cần phải lao động chứ không ai bày cỗ sẵn để ăn được. Do đó việc các thành viên đóng góp lời giải là đáng quý rồi, còn ai không hiểu thì hỏi.

Mình đề nghị bạn Uchiha sisui post bài đúng theo quy định và giải bài nào thì ghi rõ ràng.

Xin đề nghị các bài toán tiếp

Bài toán 14 (Vô địch Nga lớp 9 vòng các tỉnh). Cho tam giác $ABC$ có tâm đường tròn Euler là $N$ và tâm nội tiếp $I$. Giả sử $A,I,N$ thẳng hàng, chứng minh rằng $\angle BAC=60^\circ$.

Bài toán 15 (Thi thử chuyên KHTN năm 2011, vòng 1, đợt 1). Cho hai đường tròn $(O)$ và $(O')$ cắt nhau tại $A,B$. $M$ di chuyển trên đường thẳng AB nhưng ở ngoài đoạn $AB$. Dựng các tiếp tuyến $MP,MQ$ của $(O)$. Chứng minh rằng đường tròn ngoại tiếp tam giác $MPQ$ luôn đi qua một điểm cố định khác $O$.

Bài toán 16 (Thi thử chuyên KHTN năm 2011, vòng 2, đợt 1). Cho tam giác $ABC$ đều nội tiếp đường tròn $(O)$, độ dài đường cao là $H$. $M$ thuộc cung nhỏ $BC$ của $(O)$. Gọi $A',B',C'$ là hình chiếu của $M$ lên $BC,CA,AB$.

Cách của thầy cũng giống hệt cách của Tuấn là tính hết ra và kết quả cuối cùng đúng như thế kia. Tuy nhiên Phước có cách giải thuần túy hình khá đẹp các bạn hãy cứ thử sức tiếp. Tuấn đề nghị một bài tiếp đi em!

Bảo đã giải mở rộng 2 ở topic Marathon hình học. Có bạn nào có lời giải khác cho bài toán gốc không ? Với lời giải mình đưa ra mình nghĩ bài toán này ở mức độ khó vừa phù hợp với kiến thức THCS. Việc phát biểu đường tròn tiếp xúc như trong đề trên báo hơi gượng ép vì cuối cùng bản chất bài toán là chứng minh hai góc bằng nhau.

Cám ơn Bảo với lời giải rất nhanh, thầy đề nghị bài mới cho topic tiếp tục

Bài toán 139 (Nguyễn Lê Phước).  Cho tam giác $ABC$ có đường tròn nội tiếp $(I)$ tiếp xúc $BC,CA,AB$ tại $D,E,F$. $DE,DF$ cắt $AB,AC$ tại $M,N$. $IE,IF$ cắt $AB,AC$ tại $P,Q$. Chứng minh rằng trung điểm của $MN,PQ,BC$ thẳng hàng.

Mở rộng 2. Cho tam giác $ABC$ nội tiếp $(O)$ và tâm nội tiếp $I$. $D$ thuộc cung $BC$ không chứa $A$ của $(O)$. $DB,DC$ cắt $(IAB),(ICA)$ tại $P,Q$ khác $B,C$. $M,N$ thuộc $BC$ sao cho $MP,QN$ cùng vuông góc với $PQ$. Chứng minh rằng tâm đường tròn $(AMN)$ nằm trên $DO$.

Bài này của Phương thực chất là một bổ đề khá quen thuộc sau

Bổ đề. Tứ giác $ABCD$ nội tiếp đường tròn $(O)$. Đường tròn $(I)$ tiếp xúc $AD,BC$ và tiếp xúc ngoài cung nhỏ $CD$ tại $M$. Đường tròn $(J)$ tiếp xúc $AD,BC$ và tiếp xúc trong cung nhỏ $AB$ tại $N$. Chứng minh rằng $MN,BD,AC$ đồng quy.

Chứng minh. Theo bổ đề Poncelet thì đường tròn $(K)$ tiếp xúc $DB,DC$ tiếp xúc ngoài cung nhỏ $CD$ thì tiếp điểm cũng là $M$. Tương tự đường tròn $(L)$ tiếp xúc $DB,DC$ tiếp xúc trong cung nhỏ $AB$ thì tiếp điểm cũng là $N$. Gọi $DB$ cắt $AC$ tại $E$ thì $E$ là tâm vị tự trong của $(K),(L)$ nên theo định lý Monge thì $M,N,E$ thẳng hàng hay $MN,BD,AC$ đồng quy.

Giải bài toán. Áp dụng bổ đề cho tứ giác $MEND$ nội tiếp. Ta thu được điều phải chứng minh.

Bài toán 138 (Mở rộng T12/471 THTT). Cho tam giác $ABC$ nội tiếp $(O)$ và tâm nội tiếp $I$. $D$ thuộc cung $BC$ không chứa $A$ của $(O)$. $DB,DC$ cắt $(IAB),(ICA)$ tại $P,Q$ khác $B,C$. $M,N$ thuộc $BC$ sao cho $MP,QN$ cùng vuông góc với $PQ$. Chứng minh rằng tâm đường tròn $(AMN)$ nằm trên $DO$.

Cám ơn Phương. Bài này mình cũng đã post trên AoPS ở đây và đáp án này cũng do mình đề nghị. Trước hết ta viết bài toán lại cho đường tròn nội tiếp cho dễ nhìn, hai cách viết chứng minh giống hết nhau

Bài toán 136'. Cho tam giác $ABC$ với đường tròn nội tiế $(I)$ tiếp xúc $BC$ tại $D$. Đường tròn qua $A,B$ tiếp xúc $(I)$ tại $M$. Đường tròn qua $A,C$ tiếp xúc $(I)$ tại $N$. $BM$ cắt $CN$ tại $P$. Chứng minh rằng $\angle PAB=\angle DAC$.

Bổ đề. Cho tam giác $ABC$ với đường tròn nội tiếp $(I,r)$ tiếp xúc $BC,CA,AB$ tại $D,E,F$. Đường tròn qua $B,C$ tiếp xúc $(I)$ tại $X$ thì

i) $\frac{XE.XF}{XD^2}=\frac{r^2}{IB.IC}.$

ii) $\frac{XE}{XF}=\frac{IB.DE^2}{IC.DF^2}.$

Chứng minh. Sử dụng chứng minh trong bài G7 SL 2002 quen thuộc, gọi $DK$ là đường kính của $(I)$ thì $XK,EF,BC$ đồng quy tại $G$. $AD$ cắt $EF$ tại $H$. Ta có $\frac{XE}{XF}.\frac{KE}{KF}=\frac{GE}{GF}=\frac{HE}{HF}=\frac{[AED]}{[AFD]}=\frac{DE}{DF}.\frac{DB}{IC}.\frac{IB}{DC}$ và chú ý $KE.IC=2r^2=KF.IB$. Vậy nên $\frac{XE}{XF}=\frac{IB.DE^2}{IC.DF^2}$ và $\frac{FX}{FK}.\frac{EX}{EK}=\frac{GX}{GK}=\frac{GD^2}{GK^2}=\frac{XD^2}{4r^2}$ và chú ý $KE.IC=2r^2=KF.IB$. Nên $\frac{XE.XF}{XD^2}=\frac{r^2}{IB.IC}.$

Hệ quả. $\dfrac{XE^2}{XD^2}=\dfrac{r^2.DE^2}{IB^2.DF^2}$ and $\dfrac{XF^2}{XD^2}=\dfrac{r^2.DF^2}{IC^2.DE^2}$.

Giải bài toán. Gọi $(I)$ tiếp xúc $CA,AB$ tại $E,F$. $XYZ$ là tam giác Ceva của $P$. Gọi $BY$ cắt $DF$ tại $K$. Ta có $\frac{YC}{YA}=\frac{[YBC]}{[YBA]}=\frac{[YBC]}{[KBD]}.\frac{[KBD]}{[KBF]}.\frac{[KBF]}{[YBA]}=\frac{BC.BY}{BD.BK}.\frac{KD}{KF}.\frac{BF.BK}{BY.BA}=\frac{BC}{BA}\frac{MD^2}{MF^2}=\frac{BC}{BA}.\frac{r^2.DF^2}{EF^2.IA^2}.$ Tương tự, $\frac{ZB}{ZA}=\frac{BC}{CA}.\frac{r^2.DE^2}{EF^2.IA^2}$. Sử dụng định lý Ceva thì $\frac{XB}{XC}=\frac{YA}{YC}.\frac{ZB}{ZA}=\frac{AB.DE^2}{AC.DF^2}$. Vì vậy nên $\frac{DB}{DC}.\frac{XB}{XC}=\frac{p-b}{p-c}.\frac{AB.DE^2}{AC.DF^2}=\frac{DF.IB}{DE.IC}.\frac{AB.DE^2}{AC.DF^2}=\frac{AB^2}{AC^2}$. Do đó $AD,AX$ đẳng giác.

Cám ơn Tuấn đã đưa ra một lời giải thú vị khác đáp án. Mình xin gửi lên lời giải của mình, khác đáp án trên báo một chút.

Lời giải. Gọi $J,K,L$ lần lượt là tâm bàng tiếp góc $A,B,C$ của tam giác $ABC$ và $AI$ cắt $BC$ tại $D$. Dễ thấy $L,P,M$ thẳng hàng và $K,Q,M$ thẳng hàng. Từ đó $\frac{LM}{KN}=\frac{LM}{DJ}.\frac{DJ}{KN}=\frac{BL}{BJ}.\frac{CJ}{CK}=\frac{AL}{AK}$, đẳng thức cuối có do định lý Ceva. Từ đó hai tam giác $ALM$ và $AKN$ đồng dạng nên $\angle MAL=\angle NAK$ hay $\angle MAB=\angle NAC$.

Mở rộng 1. Cho tam giác $ABC$ và $P$ nằm trong tam giác sao cho nếu $D,E,F$ là hình chiếu của $P$ lên $BC,CA,AB$ thì $AD,BE,CF$ đồng quy. Gọi $AQ,AR$ là đường kính của $(APB),(APC)$. Lấy $M,N$ trên $BC$ sao cho $QM\parallel RN\parallel AP$. Chứng minh rằng $\angle PAM=\angle PAN$.

Bài toán T12/471 THTT đã đăng lời giải trên số 475. Mình xin phép đăng đề lên để thảo luận. Mình có tìm ra một số mở rộng cho bài toán này. Theo mình đề bài nên viết như sau sẽ đẹp hơn trên báo

Bài toán T12/471. Cho tam giác $ABC$ có tâm nội tiếp $I$. Gọi $AP,AQ$ là đường kính của các đường tròn $(AIB),(AIC)$. $M,N$ thuộc $BC$ sao cho $PM\parallel QN\parallel AI$. Chứng minh rằng $\angle MAB=\angle NAC$.

Bài toán 10 (TTT2 số 165). Cho tam giác $ABC$ nội tiếp $(O)$ với $AB<AC$. Tiếp tuyến tại $A$ của $(O)$ cắt $BC$ tại $T$. $AD$ là đường kính của $(O)$. $DB$ cắt $OT,AT$ tại $E,F$. $EO$ cắt $(AEF)$ tại $G$. Chứng minh rằng tâm nội tiếp tam giác $AGB$ nằm trên $(O)$.

(Bài này đã hết hạn trên TTT2 nhưng mình thấy đáp án trên báo hơi dài, hôm qua có một bạn giải ngắn gọn hơn) 

Cám ơn em, để thầy sửa lại bài toán 9 cho không trùng lặp. Xin đưa ra lời giải của mình cho bài toán 7.

Lời giải bài toán 7. 1) Ta có $\angle DEC=\angle DMC=\angle DFB$ và $\angle ECD=\angle FBD$ nên hai tam giác $DBF$ và $DCE$ đồng dạng g.g. Từ đó $\angle EMC=\angle EDC=\angle FDB=\angle FMB$ nên $E,M,F$ thẳng hàng. 

Bài toán 12 (Tập huấn đội Hàn Quốc 2017). Ba đường tròn $(K_a),(K_b),(K_c)$ tiếp xúc ngoài đôi một. Ba đường tròn $(I_a),(I_b),(I_c)$ tiếp xúc ngoài đôi một. Trong đó $(K_a)$ tiếp xúc ngoài $(I_b),(I_c)$ tại $B_a,C_a$. Tương tự có $C_b,A_b, A_c,A_b$. Chứng minh rằng sáu điểm  $B_a,C_a,C_b,A_b, A_c,A_b$ đồng viên.

Bài toán 134 là một mở rộng của bài chọn đội tuyển Mỹ mình đã post ở đây trong #11 và các lời giải ở #12,#13 và #15.

Ta xét một bài toán tổng quát hơn của bài toán 135, có thể coi là bổ đề.

Bài toán 135'. Cho tam giác $ABC$ và $P$ nằm trong tam giác. $PA,PB,PC$ cắt $(O)$ tại $D,E,F$. $X,Y,Z$ đối xứng $D,E,F$ qua trung điểm $BC,CA,AB$. Chứng minh rằng $(XYZ)$ đi qua trực tâm $H$ của $ABC$.

Giải. Vì $D,X$ đối xứng qua trung điểm $BC$ nên hai tam giác $ABC$ và $ADX$ có chung trung tuyến hay có chung trọng tâm $G$. Từ đó $X$ là ảnh vị tự trung điểm $U$ của $AD$ qua phép vị tự tâm $G$ tỷ số $-2$. Tương tự $Y,Z$ là ảnh vị tự tâm $G$ tỷ số $-2$ của $V,W$ lần lượt là trung điểm của $BE,CF$. Dễ thấy $O,U,V,W$ nằm trên đường tròn đường kính $OP$ nên $(XYZ)$ đi qua ảnh vị tự của $O$ trong qua phép vị tự tâm $G$ tỷ số $-2$ chính là $H$. Ta hoàn tất chứng minh,

Trở lại bài toán 135. Ta chỉ cần $P$ di chuyển trên một đường thẳng cố định đi qua $A$. Gọi đường thẳng đó cắt $(O)$ tại $L$ thì đường tròn $(HRS)$ luôn đi qua đối xứng của $L$ qua trung điểm $BC$ cố định nên tâm của $(HRS)$ thuộc một đường thẳng cố định.

Mình xin đề nghị bài tiếp.

Bài toán 136. Cho tam giác $ABC$ nội tiếp đường tròn $(O)$ đường tròn bàng tiếp góc $A$ là $(J)$ tiếp xúc $BC$ tại $D$. Đường tròn qua $A,B$ tiếp xúc $(J)$ tại $M$. Đường tròn qua $A,C$ tiếp xúc $(J)$ tại $N$. $BM$ cắt $CN$ tại $P$. Chứng minh rằng $\angle PAB=\angle DAC$.

Cám ơn em, các em cứ đề xuất các đề thi cấp 3 hoặc hsg thành phố và tỉnh thoải mái vào topic, miễn là theo tiêu chí đẹp và có giá trị ôn thi chuyên và phù hợp chương trình THCS. Mình hơi nhiều việc nên không update thường xuyên nhưng mình vẫn cố hết sức giữ lửa cho topic. Xin đề nghị các bài toán tiếp.

Bài toán 7 (Chuyên Vĩnh Phúc 2016 vòng 2). Cho tam giác $ABC$ nhọn nội tiếp đường tròn $(O)$ với $AB<AC$. Gọi $M$ là trung điểm $BC$. $AM$ cắt $(O)$ tại điểm $D$ khác $A$. Đường tròn ngoại tiếp tam giác $MDC$ cắt đường thẳng $AC$ tại $E$ khác $C$. Đường tròn ngoại tiếp tam giác $MDB$ cắt đường thẳng $AB$ tại $F$ khác $B$.

Bài toán 133' của Khánh có thể viết dưới dạng tứ giác như sau

Bài toán 133'. Cho tứ giác $ABCD$ với $P,M,N$ lần lượt thuộc $AB,BC,AD$. $PC,PD$ lần lượt cắt $AM,BN$ tại $Q,R$. Chứng minh rằng $DQ,CR,MN$ đồng quy.

Giải. Gọi $MN$ cắt $ABPD,PC$ lần lượt tại $G,S,T$. Ta thấy $(PS,DR)=N(PS,DR)=(PG,AB)=M(PG,AB)=M(PT,QC)=(PT,QC)$ suy ra $DQ,CR,MN$ đồng quy.

Cảm ơn Quân và Khánh, bài toán 133 thầy chế lại từ đây http://artofproblems...nity/c6h1279917, mục đích của thầy là lấy điểm $R$ thuộc $MN$ sao cho $AR\perp EF$ rồi sau đó chứng minh $BQ,CP$ đi qua $R$ nhưng Quân chứng minh cách khác đẹp. Chú ý rằng bài toán này và bài toán của Khánh có thể đúng với $H$ bất kỳ thay vì trực tâm. Nhưng để chứng minh $AR\perp EF$ thì cần $H$ là trực tâm.

Bài toán 134. Cho tam giác $ABC$ và $DEF$ là tam giác pedal của $P$ bất kỳ. $(DEF)$ cắt $BC$ tại $G$ khác $D$. Đường thẳng qua $P$ vuông góc với $EF$ cắt $DE,DF$ tại $M,N$. Đường tròn $(DMN)$ cắt $(DEF)$ tại $Q$ khác $D$. Lấy $T$ sao cho $TM\perp AC,TN\perp AB$. $AT$ cắt $BC$ tại $S$. Chứng minh bốn điểm $A,Q,G,S$ đồng viên.

Cám ơn Khánh về lời giải rất ngắn gọn. Bài này thầy dạy đội tuyển KHTN đã lâu rồi nên chưa tìm lại được link gốc. Mình xin đề nghị bài tập tiếp cho topic tiếp tục

Bài toán 133 (Chế lại từ AoPS). Cho tam giác $ABC$ nhọn với trực tâm $H$. Một đường thẳng qua $H$ cắt cạnh $CA,AB$ tại $E,F$. Một đường thẳng qua $H$ song song $BC$ cắt $CA,AB$ tại $M,N$. $HB,HC$ lần lượt cắt $EN,FM$ tại $P,Q$. Chứng minh rằng $BQ,CP,MN$ đồng quy.

Cám ơn Việt và Quân, thầy đề nghị bài tiếp cho topic tiếp tục

Bài toán 132. Cho tam giác $ABC$ nội tiếp đường tròn $(O)$ với đường kính $AD,BE,CF$. $P$ là điểm bất kỳ. $PD,PE,PF$ cắt $(O)$ tại $X,Y,Z$ khác $D,E,F$. Gọi $U,V,W$ là tâm Euler của tam giác $XBC,YCA,ZAB$. Chứng minh rằng đường tròn ngoại tiếp tam giác $UVW$ đi qua tâm Euler của tam giác $ABC$.

Cám ơn Khánh bài toán gốc ở đây phần chú ý trong #3 tại đây và lời giải ở trong #4, xin trích lại lời giải của Luis González

Lời giải khác bài toán 129. Gọi các tiếp tuyến của $(ABC)$ cắt nhau tại $A',B',C'$. Chú ý $\angle ACE=\angle ACX=\angle ABZ=\angle ABF$ và $\angle ACB'=\angle ABC,$ $\angle ABC'=\angle ACB$ nên $C(Y,E,B,B')=B(Z,F,C,C')$ suy ra $B(Y,E,C,B')=C(Y,E,B,B')=B(Z,F,C,C')=C(Z,F,B,C')$. $Q \equiv BY \cap CZ,$ $P \equiv BE \cap CF$ và $K \equiv BB' \cap CC'$ thẳng hàng.

Mình xin đề nghị bài tiếp.

Bài toán 130 (Từ đề thi Ba Lan). Cho lục giác $ABCDEF$ có các cạnh bằng nhau và $\angle A+\angle C+\angle E=\angle B+\angle D+\angle F$. Chứng minh rằng $AD,BE,CF$ đồng quy.

Cám ơn Khánh đã dẫn lại link. Gốc gác bài toán 128 là mình tổng quát hóa tính chất điểm Prasolov http://www.artofprob...h453505p2549205 và đã post nó ở đây http://www.artofproblemsolving.com/community/c6h455311. Như vậy là Bảo đã đưa ra tổng quát hơn nữa rất thú vị. Vậy nhờ Bảo dịch lại đáp án của mình sang tiếng Việt và post lên điên đàn. 

Mình đã nhận được ảnh từ bạn Đỗ Hoàng Việt lời giải cho bài toán 127 bằng hình học không gian thú vị, xin đăng lại ảnh đó, nhưng lưu ý bạn cần dùng latex và nên gõ lại đáp án cẩn thận.

Mình xin đề xuất bài mới.

Bài toán 129 (AoPS). Cho tam giác $ABC$. $D$ và $X$ lần lượt nằm trong và nằm ngoài tam giác sao cho $\angle DBC=\angle DCB=\angle XBC=\angle XCB=\theta$. Dựng tương tự các điểm $E,F,Y,Z$. Ta biết rằng $AD,BE,CF$ đồng quy tại $P$ và $AX,BY,CZ$ đồng quy tại $Q$. Chứng minh rằng $PQ$ đi qua điểm cố định khi $\theta$ thay đổi.