Bài hình ngày 2 nằm trong chuyên đề về đối xứng trục của thầy Hùng đăng trên báo toán học tuổi trẻ tháng này và tháng trước.

Câu a, giải như anh Phương là chuẩn rồi, câu b, có thể giải ngắn gọn như sau.

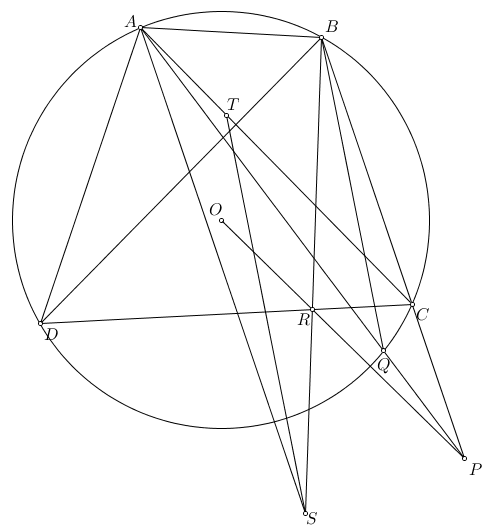
Do $BP,BQ$ đẳng giác nên $\angle BQE=\angle PBE$ suy ra $\triangle BPE\sim \triangle QBE$, từ đó $BE^2=EP\cdot EQ$

Gọi $F$ là giao điểm của $EM$ với $(O)$. Theo hệ thức lượng trong tam giác vuông thì $EP\cdot EQ=BE^2=EM\cdot EF$ suy ra tứ giác $PQFM$ nội tiếp.

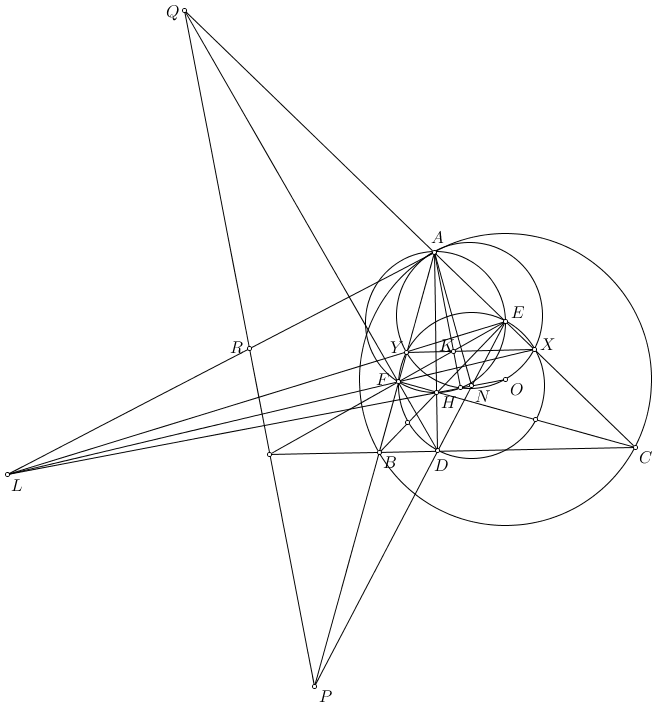
Do đó $\triangle QME\sim \triangle FPE$ (góc - góc) suy ra $\triangle RNM\sim \triangle OPE$ (đồng dạng trung tuyến)

Từ đó đường thẳng qua $P$ vuông góc với $RN$ đi qua $(O)$. Xét phép đối xứng trục $Đ_{AD}:N\to M,R\to S,O\to T$ ($T$ đối xứng $O$ qua $AD$). Ta có đpcm.

Hình vẽ bài toán

$\textbf{Lời giải.}$ Gọi $Y$ là trung điểm $PQ$.

Ta có $\angle PQB=180^\circ-\angle PAB=\angle BCD, \angle QBP=90^\circ-\angle BPA=90^\circ-\frac{1}{2}\cdot \angle BKA=\angle BKC$.

Do đó $\triangle QPB\sim \triangle CBK$ (góc - góc) suy ra $\frac{KC}{BC}=\frac{QB}{QP}\Rightarrow \frac{DC}{BC}=\frac{QB}{QY}$.

Từ đó $\triangle DBC\sim \triangle BYQ$ (cạnh - góc -cạnh) suy ra $\angle QYB=\angle DBC=\angle DCN=\angle BMC$. Do đó tứ giác $YBMN$ nội tiếp.

Gọi $Z$ là giao điểm của $PA$ với $BQ$ thì $\angle PZB=90^\circ$. Do $\angle ZYB=\angle YZQ-\angle YBQ=\angle BCD-\angle BDC=\angle BDZ$ nên tứ giác $YZBD$ nội tiếp suy ra $\angle BYD=90^\circ$.

Mặt khác do $\angle YBD=\angle ZBD-\angle ZBY=90^\circ-\angle BDA-BDC=\angle ODB$ nên $OD\parallel BY$.

Do đó $YD$ là tiếp tuyến tại $D$ của $(O)$.

Gọi $X$ là giao điểm của $YD$ với đường tròn $(BMN)$. Do tứ giác $YBMX$ nội tiếp nên $\angle BMX=90^\circ$ suy ra $MX\perp CD$ hay $MX\parallel PQ$.

Từ đó suy ra $M(XYPQ)=-1$ hay tứ giác $SYXT$ điều hòa kéo theo $XY$ đi qua $R$ hay $RD$ là tiếp tuyến với $(O).\ \blacksquare$

Như vậy thầy Hùng đã đưa ra lời giải bài cũ trong tuần 3 tháng 9 và kèm theo đó là bài toán mới, xin trích dẫn lại bài toán đó.

Cho hình thang cân $ABCD$ nội tiếp trong đường tròn $(O).K$ là trung điểm $CD.AD$ cắt đường tròn $(K)$ đi qua $A,B$ tại $P$ khác $A.Q$ là trực tâm tam giác $PAB$. Tiếp tuyến tại $C$ của $(O)$ cắt $AB,PQ$ lần lượt tại $M,N.MQ,NP$ lần lượt cắt đường tròn $(L)$ ngoại tiếp tam giác $BMN$ tại $S,T$ khác $M$. Tiếp tuyến tại $S,T$ của $(L)$ cắt nhau tại $R$. Chứng minh rằng $RD$ tiếp xúc $(O)$.

Hình vẽ bài toán

Câu 3. a, Do $EF\parallel BC$ nên $\angle FPC=\angle FCE$. Mặt khác dễ thấy $\triangle OCE\sim \triangle BAH$ nên $\frac{OE}{EC}=\frac{BH}{AH}$. Từ đó suy ra $\frac{MH}{HB}=\frac{EC}{EF}$ nên $\triangle FEC\sim \triangle BHM$ (cạnh - góc - cạnh). Do đó $\angle BMQ=\angle FCE=\angle FPC$ nên tứ giác $MQBP$ nội tiếp.

b, Gọi $R$ là giao điểm của $EM$ với $(K)$. Dễ thấy chỉ cần chứng minh tứ giác $RSMT$ điều hòa $\Leftrightarrow P(RMAH)=-1$. Mặt khác do $M$ là trung điểm $AH$ nên ta chỉ cần chứng minh $PR\parallel AH$. Điều này tương đương với chứng minh $\angle PQM+\angle EMQ=180^\circ$.

Do $\angle PQM=90^\circ+\angle BPQ=90^\circ+\angle BMH$ nên ta chỉ cần chứng minh $\angle BME=90^\circ$. Kết quả này quen thuộc!

Em hơi nhầm lẫn, cho em xin lỗi!

Hình vẽ bài toán

$\textbf{Lời giải.}$ Gọi $D,E$ lần lượt là giao điểm của $AO$ với các đường tròn $(O)$ và $(K). X$ là giao điểm của $CM$ với $BN$.

Gọi $H$ là giao điểm của $MN$ với $BC$.

Áp dụng định lí Pascal cho hệ điểm $\bigl(\begin{smallmatrix} B & M &C \\ M & B & N \end{smallmatrix}\bigr)$ ta suy ra $X,H,P$ thẳng hàng tức $P$ thuộc $XH$.

Áp dụng định lí Pascal cho hệ điểm $\bigl(\begin{smallmatrix} M & C &N \\ B& N & C \end{smallmatrix}\bigr)$ ta suy ra $X,H,Q$ thẳng hàng tức $Q$ thuộc $XH$.

Do đó $PQ\equiv XH$ hay $X,H$ thuộc $AO$. Do $HM\cdot HN=HB\cdot HC=HD\cdot HA$ nên tứ giác $AMDN$ nội tiếp.

Mặt khác do $O$ là trung điểm $AD$ nên hiển nhiên $OL\perp AO$. $\blacksquare$

Như vậy thầy Hùng đã đưa ra lời giải bài cũ tại tuần 2 tháng 9 và kèm theo đó là bài toán mới, xin trích dẫn lại bài toán đó.

Cho tam giác $ABC$ nhọn với tâm ngoại tiếp $O.(K)$ là đường tròn ngoại tiếp tam giác $OBC$. Tiếp tuyến tại $B,C$ của $(K)$ lần lượt cắt $AO$ tại $P,Q$. Lấy $M$ khác $B$ thuộc $(K)$ sao cho $PM$ tiếp xúc $(K)$. Lấy $N$ khác $C$ thuộc $(K)$ sao cho $QN$ tiếp xúc $(K)$. Gọi $L$ là tâm đường tròn ngoại tiếp tam giác $AMN$. Chứng minh rằng $OL\perp AO$.

Hình vẽ bài toán

Hình vẽ bài toán

$\textbf{Lời giải.}$ Gọi $N$ là giao điểm của $BQ$ với $AC.M$ là giao điểm của $BS$ với $(O)$. Do $R$ là giao điểm của $OP$ với $CD$ nên $D,M,P$ thẳng hàng.

Xét cực đối cực với đường tròn $O$. Do $N,R$ lần lượt liên hợp với $P$ nên $NR$ là đường đối cực của $P$ đối với $(O)$. Do đó mà $NR\parallel CM\parallel BD$.

Đường thẳng qua $C\parallel AB$ cắt $BM$ tại $H$. Do $NR\parallel BD$ nên $\angle NRC=\frac{1}{2}\angle BRC$ suy ra $\angle HRN=\angle NRC=\angle NCH$ nên tứ giác $NCRH$ nội tiếp.

Từ đó $\angle NHC=\angle NCH$ nên $NH=NC$. Mặt khác do $\triangle BHC\sim \triangle SBA$ (góc - góc), $BC\parallel AS, ST\parallel BN$ nên $TA=TB$. $\blacksquare$

Như vậy thầy Hùng đã đưa ra lời giải bài cũ tại tuần 1 tháng 9 và kèm theo đó là bài toán mới, xin trích dẫn lại bài toán mới.

Cho tứ giác $ABCD$ nội tiếp trong đường tròn $(O). BC$ cắt trung trực $BD$ tại $P.AP$ cắt $(O)$ tại $Q$ khác $A. CD$ cắt $OP$ tại $R$. Trên $BR$ lấy $S$ sao cho $AS\parallel BP$. Lấy $T$ thuộc $AC$ sao cho $ST\parallel BQ$. Chứng minh rằng $TA=TB$.

Hình vẽ bài toán

$\textbf{Lời giải.}$ Ta có $\angle A_2C_1A=\angle A_2B_1A,\angle A_2BC_1=\angle A_2CB_1$ nên $\triangle A_2C_1B\sim \triangle A_2B_1C$ (góc - góc). Do đó

\[\frac{A_2B}{A_2C}=\frac{BC_1}{CB_1}\]

Suy ra \[\frac{A_4B}{A_4C}=\frac{[BA_2A_3]\cdot CA_2}{[CA_2A_3]\cdot BA_2}=\frac{BA_3\cdot CA_2}{CA_3\cdot BA_2}=\frac{BA_3\cdot CB_1}{CA_3\cdot BC_1}\]

Từ đây áp dụng định lí $\text{Ceva}$ cho $\triangle ABC$ với $AA_1,BB_1,CC_1$ và $AA_3,BB_3,CC_3$ đồng quy ta suy ra

\[\prod \frac{A_4B}{A_4C}=1\]

Do đó theo bổ đề $\text{Ceva}$ trong đường tròn ta suy ra $AA_4,BB_4,CC_4$ đồng quy.

PS. Kỳ thực nếu sử dụng lượng giác thì sẽ gọn hơn!

Lời giải bài toán 93 đã có ở đây http://artofproblems...endicular_to_bc

Lời giải của em. Tính chất sau quen thuộc : Gọi $X,Y$ lần lượt là điểm chính giữa cung $AC$ không $B$ và cung $AB$ không chứa $C$.

Khi đó ta có $IE\cdot BX=IF\cdot CY$.

Gọi $S$ là giao điểm các tiếp tuyến tại $B,C$ của $(O)$ thì $Z$ là điểm chính giữa cung $BC$ không chứa $O$ của $(K)$.

Đường thẳng qua $Z$ song song với $EF$ cắt $CF,BE$ tại $T,S$. Chú ý các cặp góc $\angle ZCF=\angle YXC,\angle ZCE=\angle BYX$ và $ZB=ZC$ dễ thấy $Z$ là trung điểm $ST$.Do đó mà $IZ$ chia đôi $EF$. Mặt khác theo định lí Protassov's thì $PI$ là phân giác $\angle BPC$ nên $PI$ đi qua điểm chính giữa cung $BC$ không chứa $O$ của $(K)$ (tức $Z$). Do đó $PI$ chia đôi $EF.\ \blacksquare$

Hình vẽ bài toán

PS. Định lí Protassov's là một kết quả quen thuộc và đã từng xuất hiện trên tạp chí THTT và trong bài viết của GGTH 2013.

Có thể tham khảo bài chứng minh sau của Jean Louis.

Như vậy thầy Hùng đã đưa ra lời giải bài cũ trong tuần 5 tháng 8 và kèm theo đó là bài toán mới, xin được trích dẫn lại bài toán mới.

Cho tam giác $ABC$ nhọn có phân giác $BE,CF$ cắt nhau tại $I$. Đường tròn $(K)$ đi qua $B,C$ và tâm ngoại tiếp $O$ của tam giác $ABC$. Đường tròn $(L)$ nằm trong tam giác tiếp xúc $CA,AB$ và tiếp xúc ngoài $(K)$ tại $P$. Chứng minh rằng $PI$ chia đôi $EF$.

Hình vẽ bài toán

Bài toán $91$ đã lâu chưa có ai giải nên mình xin được phép đưa ra lời giải để tiếp tục topic.

$\boxed{\text{Lời giải bài toán 91}}$  Gọi $X,Y$ lần lượt là đối xứng của $B,C$ qua $P,Q$. Do $MPKQ$ là hình bình hành nên $K$ là trung điểm $XY$. Mặt khác do $\angle XBA=\angle YCA$ nên $\triangle BAX\sim \triangle CAY$ suy ra $\angle BAX=\angle CAY$. Gọi $E',F'$ lần lượt là giao điểm của $AX,AY$ với đường tròn $(O)$ thì $E'F'\parallel BC$. Gọi $H$ là giao điểm của $CE'$ và $BF'$. Đường thẳng qua $H$ song song với $XY$ cắt $AE',AF'$ lần lượt tại $S,T$. Gọi $S',T'$ lần lượt là hình chiếu của $H$ lên $AS,AT.L$ là giao điểm khác $A$ của $AH$ với đường tròn $(O)$. Dễ thấy $\triangle S'HT'\sim \triangle E'LF'$ (g.g) nên \[\frac{HS'}{HT'}=\frac{LE'}{LF'}=\frac{AC.HL}{HC}.\frac{HB}{AB.HL}=\frac{AC}{AB}=\frac{AY}{AX}=\frac{AT}{AS}\] Do đó $HS'.AS=HT'.HT$ suy ra $[HAS]=[HAT]$ từ đó $H$ là trung điểm $ST$. Theo bổ đề hình thang $AH$ đi qua trung điểm $K$ của $XY$ hay $AK$ đi qua $H$ là giao điểm của $CE',BF'$. Lại có $\angle BAE'=\angle CAF'$ cố định nên các điểm $E'F'$ cố định trên đường tròn $(O)$ do đó $AK$ đi qua một điểm cố định. $\blacksquare$

Lần này mình sẽ không đề xuất bài toán mới nữa mà sẽ dành công việc này cho thầy Hùng!

Em nghĩ cái này liên quan đến đường đi ngắn nhất từ điểm $O$ đến $P$ và với mô hình kiểu này thì ta có một bài mẫu khá điển hình là bài $VNTST\ 2003$ và em nghĩ có lẽ bài liên quan đến bài toán đó!

Cho điểm $P(m,n)$ với $m,n$ là các số tự nhiên. Giả sử $P$ nằm trên đường thẳng $L:y=px+q$ với $p,q$ là các số tự nhiên. 

Một đường đi từ đỉnh $(0,0)$ đến đỉnh $P$ trong đó mỗi bước đi sẽ theo véctơ $(0,1)$ hoặc $(1,0)$. Chứng minh rằng số các đường đi chỉ cắt $L$ tại một điểm duy nhất là $P$ bằng $\frac{q}{m+n}.\binom{m+n}{m}$

Bài tuần này Hoàng giải vậy thì đẹp rồi, sau đây là lời giải của em!

Hình vẽ bài toán

Lời giải bài toán. Gọi $I$ là trung điểm $AP$ thì $I$ là tâm đường tròn đường kính $AP$. Từ đó ta có $\angle MAP=\angle MAH=\angle PMC$ nên đường tròn $(AP)$ tiếp xúc $BC$.

Từ đó $BL.BA=CK.CA=CM^2\implies AR.AB=AQ.AC=2CM^2$ nên tứ giác $BRQC$ nội tiếp.

Gọi $S$ là giao điểm của $AM$ với đường tròn $(ABC)$. Ta có $\angle ASB=\angle ACB=\angle ARQ$ nên tứ giác $BRNS$ nội tiếp $\implies AN.AS=AR.AB=2CM^2$.

Mặt khác do tứ giác $ABSC$ nội tiếp nên $AM.MS=CM^2\implies AN.AS=2AM.MS\implies \frac{AM}{AN}=\frac{AS}{2MS}$

Gọi $T$ là điểm đối xứng của $A$ qua $O, F$ là giao điểm của $PO$ với $AH$ thì $AFTP$ là hình bình hành suy ra $AF=PT$. Gọi $X$ là giao điểm của $OM$ với $TS$. Do $MX\parallel PR\perp BC,MP\parallel XT\perp AM$ nên $MPTX$ là hình bình hành $\implies AF=PT=MX$.

Gọi $E$ là trung điểm $ST$ thì $OE\parallel MS$ nên theo định lí Thales thì $\frac{OM+AF}{AF}=\frac{OX}{MX}=\frac{OE}{MS}=\frac{AS}{2MS}=\frac{AM}{AN}$.

Từ đó theo định lí Thales đảo thì $O,N,F$ thẳng hàng hay $PN$ đi qua $O$. $\blacksquare$

Xin lỗi mọi người vì bài toán tuần này được mình đưa lên hơi muộn!

Lời giải bài toán cũ đã có tại tuần 4 tháng 8 và kèm theo đó là bài toán mới, xin được trích dẫn lại bài toán đó

Cho tam giác $ABC$ có trung tuyến $AM$. Lấy điểm $H$ sao cho $AH\perp BC$ và $HM\perp AM.P$ đối xứng $H$ qua $M.K,L$ là hình chiếu của $P$ lên cạnh $CA,AB$. Trên cạnh $CA,AB$ lấy $Q,R$ sao cho $AQ=2KC$ và $AR=2BL.AM$ cắt $QR$ tại $N$. Chứng minh rằng $PN$ đi qua tâm đường tròn ngoại tiếp tam giác $ABC$.

Hình vẽ bài toán

Bổ đề. Cho $p$ là số nguyên tố có dạng $4k+3$. Khi đó $p\mid x^2+y^2\iff p\mid x,p\mid y$.

Chứng minh. Dễ thấy chỉ cần chứng minh cho trường hợp cả hai số không chia hết cho $p$. Theo định lí $Fermat$ nhỏ thì:

$x^{p-1}\equiv y^{p-1}\equiv 1\pmod p\implies x^{p-1}+y^{p-1}\equiv 2\pmod p\implies x^{4k+2}+y^{4k+2}\equiv 2\pmod p$

$\iff (x^2)^{2k+1}+(y^2)^{2k+1}\equiv 2 \pmod p$ (mâu thuẫn do $p\mid x^2+y^2$. Bổ đề được chứng minh.

Quay lại bài toán. Giả sử $A=\frac{x^2+y^2}{x+y}$ có ước nguyên tố $p$ có dạng $4k+3\implies p\mid x^2+y^2$.

Theo bổ đề trên thì $p\mid x,p\mid y$. Đặt $x=pa,y=pb$ thì $A=p(\frac{a^2+b^2}{a+b})$.

Do đó ta chỉ cần xét trong trường hợp $A$ không có ước nguyên tố dạng $4k+3$.

Do $A\mid 1978=2.3.11.17$ nên ta xét với $A=1$ hoặc $A=2$.

Nếu $A=1$ thì $x^2+y^2=x+y$, do $x,y$ nguyên nên $x^2+y^2\geq x+y$. Dấu $"="$ xảy ra $\iff x=y=1.$

Nếu $A=2$ thì $x^2+y^2=2x+2y$, do $x,y$ nguyên nên dễ thấy $x=y=2$. Do đó $x=y.\ \blacksquare$

Bài toán $90$ đúng trong trường hợp tổng quát hai điểm liên hợp đẳng giác, bài này đã được anh Huy đưa lên AoPS tại đây và có lời giải của Telv Cohl.

Đề xuất bài toán tiếp theo khá nhẹ nhàng để tiếp tục topic.

$\boxed{\text{Bài toán 91}}$ (Own) Cho hai đường tròn $(O)$ và $(O_1)$ cắt nhau tại $B,C;M$ là trung điểm $BC$. Điểm $A$ chạy trên $(O)$ và khác $B,C.AB,CA$ theo thứ tự cắt $(O_1)$ tại $F,E;P,Q$ lần lượt là hình chiếu của $A$ lên $BE,CF$. Dựng hình bình hành $MPKQ$. Chứng minh rằng $AK$ luôn đi qua một điểm cố định.

$\boxed{\text{Lời giải bài toán 89.}}$ Gọi $A_6$ là giao điểm của $AA_0$ với $(N).A_3'$ là giao điểm của $AA_1$ với $(N)$.

Ta có $\angle AA_6A_3'=\angle AA_1A_0=A_3'AA_2$ nên $AA_2$ tiếp xúc đường tròn $(AA_3'A_6)$.

Mặt khác $\angle AC_0B_0=\angle ACB=\angle CAA_2$ nên $AA_2$ tiếp xúc đường tròn $(AB_0C_0)$.

Từ đó các đường tròn $(AA_3'A_6)$ và $(AB_0C_0)$ tiếp xúc nhau. Theo định lí về tâm đẳng phương ta suy ra $B_0C_0,AA_2,A_3'A_6$ đồng quy.

Do đó $A_3'A_6$ đi qua $A_2$. Từ đó $A_2A_3'A=90^\circ$ nên $A_3\equiv A_3'$.

Do $A_4$ và $N$ lần lượt là tâm đường tròn $\text{Euler}$ của tam giác $ABC$ và đường tròn đường kính $AA_2$, để ý rằng $A_3$ là giao của hai đường tròn này nên $A_5$ đối xứng với $A_3$ qua đoạn nối tâm sẽ là giao điểm thứ hai của hai đường tròn. Từ đó $\angle AA_5A_2=90^\circ$. 

Gọi $A_2A_0$ cắt $(N)$ tại điểm $A_5'$ khác $A_0$. Ta có $\mathcal{P}_{A_2/(N)}=A_2A^2=A_2A_5'.A_2A_0$ nên $\angle AA_5'A_2=90^\circ$.

Do đó $A_5\equiv A_5'$.

Gọi $X$ là giao điểm của $A_5$ với $(N)$. Do $\angle AA_5A_0=90^\circ$ nên $X$ đối xứng với $A_0$ qua $N$, từ đó $X$ thuộc trung trực $BC$.

Từ đây áp dụng định lý $\text{Ceva}$ dạng lượng giác cho các tam giác $AB_1C_1,BC_1A_1,CA_1B_1$. Chú ý rằng 

\[\frac{\sin \angle XB_1C_1}{\sin \angle ZB_1A_1}.\frac{\sin \angle ZA_1B_1}{\sin \angle YA_1C_1}.\frac{\sin \angle YC_1A_1}{\sin \angle XC_1B_1}=1\]

và các cặp góc bằng nhau $\angle XB_1A_1=\angle YA_1B_1,\angle XC_1B_1=\angle ZA_1B_1,\angle YC_1A_1=\angle ZB_1A_1$ ta suy ra

\[\prod \frac{\sin \angle XAB_1}{\sin \angle XAC_1}=1\]

Từ đó theo định lý $\text{Ceva}$ dạng lượng giác ta suy ra $AX,BY,CZ$ đồng quy hay $AA_5,BB_5,CC_5$ đồng quy. $\blacksquare$

Đề xuất bài toán mới để tiếp tục topic!

$\boxed{\text{Bài toán 90}}$ (Đặc biệt hóa) Cho tam giác $ABC$, trọng tâm $G$, điểm $\text{Lemoine}$ $L$. $U,V$ lần lượt là hình chiếu của $L,G$ trên $BC$. Gọi $J$ là giao điểm khác $A$ của đường tròn $(AUV)$ và đường tròn $(ABC)$. $AT$ là đường kính của đường tròn $(ABC)$. Chứng minh rằng $JT$ chia $LU,GV$ cùng tỉ số.

Tác giả bài toán tổng quát là "đại ca" Trần Quang Huy!

Lời giải của em hoàn toàn dùng được trong trường hợp tổng quát và trong trường hợp này nó có vẻ đơn giản hơn! Sau đây là lời giải chi tiết.

Gọi $X,Y$ lần lượt là hình chiếu của $S$ lên $CA,AB$.

Do $AS$ đi qua $O$ là tâm đường tròn ngoại tiếp tam giác $ABC$ nên $XY\parallel BC$. Mặt khác do $AE.AC=AP.AD=AF.AB$ nên tứ giác $BCEF$ nội tiếp.

Từ đó tứ giác $XEYF$ nội tiếp. Do đó nếu gọi $K$ là giao điểm của $XY,EF$ thì $KX.KY=KE.KF$ nên $K$ thuộc trục đẳng phương của $(AS)$ và $(AP)$.

Do đó $AK\perp SP$ hay $AK\parallel MN$ suy ra $A(NMQK)=-1$. Từ đây theo định lí Brocard ta có điều phải chứng minh. $\blacksquare$

Hình vẽ bài toán

$\textbf{Lời giải.}$ Gọi $X,Y$ lần lượt là trung điểm của $AC,AB.K$ là giao điểm của $XY$ với $EF$. Ta sẽ chứng minh $K$ là trực tâm của tam giác $ALN$.

Ta có $QF.QD=QA.QC$ nên $Q$ thuộc trục đẳng phương của $(ABC)$ và $(N)$. Tương tự ta suy ra $PQ$ là trục đẳng phương của $(ABC)$ và $(N)$.

Do đó $PQ$ vuông góc với đường thẳng $Euler$ của tam giác $ABC$.

Gọi $O$ là tâm đường tròn ngoại tiếp tam giác $ABC$. Do $KX.KY=KE.KF$ nên $K$ thuộc trục đẳng phương của $(AO)$ và $(AH)$.

Từ đó $AK$ vuông góc với đường thẳng $Euler$ của tam giác $ABC$ hay $AK\parallel PQ$. Mặt khác do $AK\perp OH$ nên $AK\perp NH$

Theo định lí $Brocard$ ta suy ra $EY,FX$ cắt nhau trên $OH$. Lại có $A(QPRK)=-1$ nên $A(QLRK)=-1$ từ đó $L$ là giao điểm của $EY,FX$.

Theo định lí $Brocard$ ta có điều phải chứng minh. $\blacksquare$

Lời giải $\boxed{\text{bài toán 87}}$ của Tev Cohl có thể tham khảo link.

Để tiếp tục topic, mình xin đề xuất một bài toán "dễ thở". Bài toán nằm trong bài viết của mình và thầy Hùng trong số báo epsilon 10.

$\boxed{\text{Bài toán 88.}}$ (Trần Quang Hùng) Cho tam giác $ABC$ cân tại $A$ có đường cao $CD$. Gọi $E,M$ là trung điểm của $BD,CE.R$ thuộc $AB$ sao cho $BR=CD.CR$ cắt $AM$ tại $K$. Chứng minh rằng $\angle CKD=90^\circ$.

PS. Mong mọi người có lời giải ngắn gọn cho bài này, mình chỉ có một lời giải thuần túy nhưng khá dài và lời giải còn lại dùng tính toán!

Bài này thì quen thuộc rồi!

$\textbf{Lời giải.}$ Giả sử $\triangle XYZ$ là tam giác tạo bởi $BC,MN,EF$. Gọi $T$ là giao điểm của $(AEF)$ với $(O)$. Do $\angle PTA=\angle PFA=\angle PEA=90^\circ$ nên $T,P,K,D$ thẳng hàng. Từ đó theo một kết quả quen thuộc thì $T$ là điểm $Miquel$ của tứ giác toàn phần $FEMNAY$. Mặt khác do $T$ là điểm $Miquel$ của tứ giác toàn phần $EFCBAX$ nên $T$ cũng là điểm $Miquel$ của tứ giác toàn phần $YMCXZE$ từ đó tứ giác $XYZT$ nội tiếp.

Đến đây thì ta chỉ cần chứng minh $\angle BTY=\angle TXY+\angle TAB$. Ta có các biến đổi góc đơn giản,

$\angle BTY=\angle NTY-\angle NTB=\angle AFE-\angle MTC \,\ \angle TXY+\angle TAB=\angle TCE+\angle TEF$

Do đó ta chỉ cần chỉ ra $\angle AFE-\angle MTC=\angle TCE+\angle TEF$ tương đương $\angle AFE=\angle AMT+\angle TEF=\angle TNA+\angle TAN=\angle TMA$ (hiển nhiên đúng do tứ giác $MNEF$ nội tiếp) .$\blacksquare$

PS. Kết quả quen thuộc ở đây liên quan đến bài toán $T12/466$ trên báo THTT của thầy. Gõ hơi chậm!

Như vậy thầy Hùng đã đưa ra lời giải bài cũ trong tuần 2 tháng 8 và kèm theo đó là bài toán mới, xin trích dẫn lại bài toán :

Cho tam giác $ABC$ nội tiếp trong đường tròn $(O).AD$ là đường kính của $(O).E,F$ là hình chiếu của $P$ bất kỳ trong tam giác lên $CA,AB.PD$ cắt trung trực $EF$ tại $K$. Đường tròn $(K)$ đi qua $E,F$ cắt $CA,AB$ lần lượt tại $M,N$ khác $E,F$. Chứng minh rằng các đường thẳng $EF,MN,BC$ cắt nhau tạo thành một tam giác có đường tròn ngoại tiếp tiếp xúc $(O)$.