$\boxed{\text{Lời giải bài toán 8}}$ 

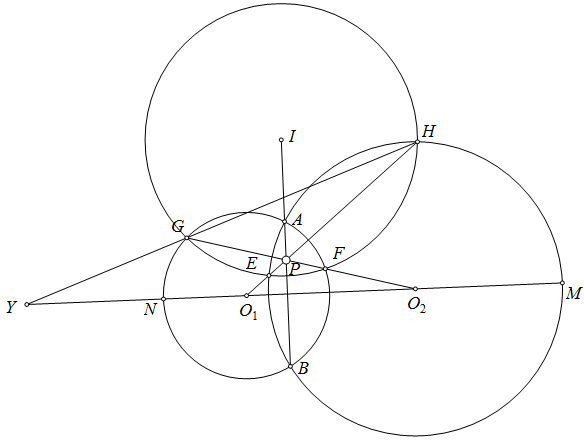
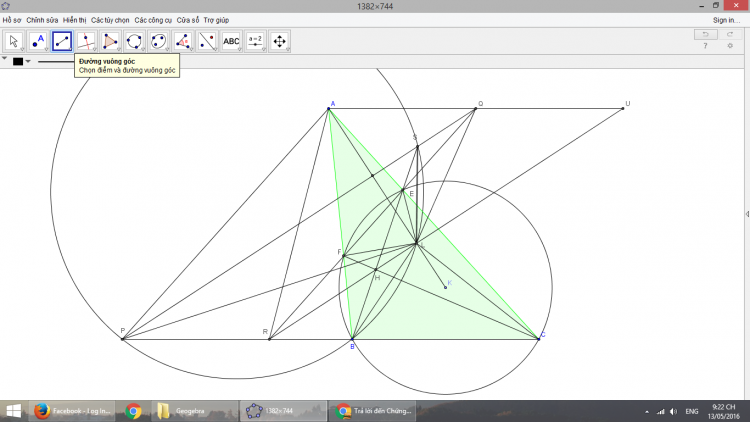
Gọi $N,M$ là giao điểm của $O_{1}O_{2}$ với $ O_{1}$ và $O_{2}$ như hình trên, $H$ là giao điểm thứ 2 của $O_{1}P$ và  $(O_{2})$, $G$ là giao điểm thứ 2 của  $O_{2}P$ và  $(O_{1})$

ta sẽ chứng minh $EM,FN$ và $AB$ đồng quy

ta có $(O_{2}PFG)=(O_{1}PEH)=-1$ nên $EF, GH, O_{1}O_{2}$ đồng quy tại $Y$

Gọi $I$ là điểm sao cho $(IPAB)=-1$ thì $IF,IG$ là tiếp tuyến của $O_{1}$  và $IE,IH$ là tiếp tuyến của $O_{2}$, $I$ thuộc $AB$ là trục đẳng phương của 2 đường tròn nên  $IE=IF=IG=IH$ nên $EFGH$ nội tiếp 

suy ra $EG,FH,O_{1}O_{2}$ đồng quy tại điểm $X$ ( theo định lý Brocard) và $(YXO_{1}O_{2})=-1$ nên $PX, O_{1}F, O_{2}E$ đồng quy.

Áp dụng định lí Ceva để ý $R_{1}^{2}=O_{1}E.O_{1}H $ và $R_{2}^{2}=O_{2}F.O_{2}G$  ta có $\frac{XO_{1}}{XO_{2}}=\frac{O_{1}E}{EP}.\frac{PF}{FO_{2}}=\frac{O_{1}H}{PH}.\frac{GP}{GO_{2}}=\frac{R_{1}^{2}}{R_{2}^{2}}.\frac{GP.O_{2}F}{PH.O_{1}E}=\frac{R_{1}^{2}}{R_{2}^{2}}.\frac{EP.O_{2}F}{FP.O_{1}E}=\frac{R_{1}^{2}}{R_{2}^{2}}.\frac{O_{2}X}{O_{1}X}$

nên $\frac{O_{1}X}{O_{2}X}=\frac{R_{1}}{R_{2}}$ nên $X$ là tâm vị tự trong của 2 đường tròn $\Rightarrow Y$ là tâm vị tự ngoài của 2 đường tròn do $(YXO_{1}O_{2})=-1$ $\Rightarrow $ theo tính chất cơ bản ta có $EFMN$ nội tiếp $\Rightarrow EM,FN,AB$ đồng quy tại tâm đẳng phương $V$ của 3 đường tròn

dễ thấy $EM,FN$  là phân giác $\angle PED$ và  $\angle PFD$ nên $EV, FV$ cũng là phân giác 2 góc này

Từ định lý phân giác ta có điều phải chứng minh.

$$\begin{array}{| l | l |} \hline Ngockhanh99k48 & 1\\ \hline IHateMath & 1\\ \hline fatcat12345 & 2\\ \hline dogsteven & 2\\ \hline baopbc & 3\\ \hline QuangDuong12011998 & 1\\ \hline xuantrandong & 1\\ \hline\end{array}$$

Bạn có chắc chắn đúng đề không vậy?  Mình vẽ hình thấy đâu có thỏa! 

Post 148.png

xin lỗi bạn, mình vừa sửa lại đề

để ý $BE$ và $CF$ đi qua trực tâm H ta có thể tổng quát bài toán trên cho 2 điểm đẳng giác

bỏ các giả thiết $O$ và $H$ là tâm đường tròn ngoại tiếp và trực tâm và thay vào đó là 2 điểm liên hợp đẳng giác bất kì 

gọi $D=BC\cap AI$ 

Do $O$ và $F$ là 2 điểm đẳng giác góc $C$ của tam giác $CKB$ nên dễ thấy $OB, FK, CL$ đồng quy tại $U$

gọi $X=FI\cap BU$

Ta có $L(B,I,X,K)=-1$ và $L(B,I,D,K)=-1$ nên $L,X,D$ thẳng hàng nên $X=LD\cap OB$ và $F,X,I$ thẳng hàng

Tương tự gọi $Y=KD\cap OC$ thì ta có $E,Y,I$ thằng hàng

áp dụng định lí Pappus cho 6 điểm $L,O,K,B,D,C$ ta có $X,I,Y$ thẳng hàng => $F,X,I,Y,E$ thẳng hàng => $E,F,I$ thẳng hàng

điều ngược lại chứng minh tương tự như trên 

ta có đpcm

cho 2 đường tròn $\odot(O)$ và $\odot(O')$ không cắt nhau . gọi $d$ là trục đẳng phương của 2 đường tròn này. 1 đường thẳng bất kì cắt  $\odot(O)$ và $\odot(O')$ lần lượt tại $X,B,Y,C$, $X,B\in (O); Y,C \in (O')$. Gọi $A$ và $T$ là 2 điểm bất kì thuộc $d$. Đường thẳng bất kì qua $T$ cắt $AB,AC$ lần lượt tại $E,F$. Đường thẳng bất kì qua $T$ cắt $AX,AY$ lần lượt tại $G,H$. Gọi $S$ là giao điểm của $GF$ và $HE$. Chứng minh $AS$ song song với $BC$

cách giải của mình k hay. Mọi người góp ý nha 

Đây là lời giải của mình:

Gọi $R$ là giao điểm $HL$ và $BC$. Qua $A$ kẻ đường thằng song song với $BC$ cắt $EF$ và $HL$ tại $Q$ và $U$.

Dễ thẩy $R, E, F, Q$ thằng hàng mà chùm $R(A,H,F,B)=-1$ nên $Q$ là trung điểm $AU$ nên $PQ$ là đường trung trực của $AL$.

$QURP$ là hình bình hành mà $AQ=QU$ nên $AQRP$ là hình bình hành nên $\angle AQF=\angle APC$ nên $\triangle AQF$ đồng dạng $\triangle APC$ mà $\triangle AEF$ đồng dạng $\triangle ABC$ nên $\frac{QE}{EF}=\frac{PB}{BC}$.

Dế chứng minh được $\triangle LEF$ đồng dạng $\triangle LBC$ nên kết hợp điều trên ta có $\Delta LQE$ đồng dạng $\Delta LPB$ suy ra $\Delta LEB$ đồng dạng $\Delta LQP$ nên $LEFQ$ nội tiếp $\Rightarrow \angle LSE=\angle LQE$ nên $\angle LSB=\angle LQR$  

Dễ thấy $LQPR$ là hình thang cân $\Rightarrow \angle LQR=\angle LPR$ vậy $\angle LSB=\angle LPB$ ta có điều phải chứng minh.

P/s: Mình làm hơi tắt, mấy bạn thông cảm

L thuộc đường đối cực của B và M nên BM là đường đối cực của L

=> IL vuông góc BM 

tương tự IK vuông góc CN

ta có đpcm

câu hình ý a khá đơn giản sử dụng $\Delta FIN$ đồng dạng $\Delta IEM$

câu hình b gọi T và H là trung điểm EF và EI, ta có $\Delta FIE$ đồng dạng $\Delta IME$ nên $\Delta FIT$ đồng dạng $\Delta IMH$ nên $\angle FIT = \angle IMH=\angle = \angle MIC =\frac{\angle B}{2}$ nên TI là tiếp tuyến của (L) $=>$  TI là trục đẳng phương của (L) và (K) mà T là trung điểm EF nên dễ suy ra được $EP= FQ$

Mình chỉ mới chứng minh được trong trường hợp $M,N,P$ là trung điểm của $BC,CA,AB$

Mình giải như sau:

Gọi

 $\odot (I)$  là đường tròn nội tiếp $\Delta ABC$

$\odot (I')$ là đường tròn nội tiếp $\Delta MNP$ 

$V$ là tiếp điểm của $\odot (I')$ và $NP$

$Q$ là tiếp điểm của đường tròn bàng tiếp $\angle A$ và $BC$

$D$ là tiếp điểm của $\odot (I)$ và $BC$

$T$ là giao điểm của $AQ$ và $\odot (I)$ thì dễ chứng minh được $MT$ là tiếp tuyến của  $\odot (I)$

Do $\Delta ABC$ đồng dạng $\Delta MNP$ nên:

$\frac{VN}{VP} = \frac{DB}{DC} =\frac{QC}{QB}$ nên $A$, $V$, $Q$ thẳng hàng

suy ra bốn điểm $A,V,T,Q$ thẳng hàng

ta có $\angle XVT = \angle AVP=\angle AQB=\angle MTQ=\angle VTX$ nên $\Delta XVT$ cân tại $X$ => $XV=XT$

 nên $X$ thuộc trục đẳng phương của  $\odot (I)$ và $\odot (I')$

tương tự $Y$ và $Z$ cũng thuộc trục đẳng phương của   $\odot (I)$ và $\odot (I')$

nên $X, Y, Z$ thẳng hàng

Cho $\Delta ABC$ nhọn có $H$ là trực tâm. Gọi $P$ và $Q$ là hai điểm bất kì tương ứng thuộc cạnh $AB$ và $AC$. Dựng $\Delta MBC$ đồng dạng với $\Delta HPQ$ . Chứng minh $HM\perp PQ$.

Gọi $G$ và $G'$ là điểm chính giữa cung lớn $BAC$ và cung nhỏ $BAC$

$N'$ đối xứng với $N$ qua $G$

$ND$ cắt $\odot (BIC)$ tại $H$.

Ta sẽ chứng minh $\odot (MPQ)$ tiếp xúc với đường tròn $\odot (BIC)$ tại $H$.

Dễ chứng minh $GB$ và $GC$ là tiếp tuyến của $\odot (BIC)$ nên $GP.GQ= GB^{2} = GN.GH= GN'.GH\Rightarrow $ tứ giác $N'PHQ$ nội tiếp $\Rightarrow MPHQ$ nội tiếp $\Rightarrow \odot (BIC)$ và $\odot (MPQ)$ có điểm chung $H$.

Ta sẽ chứng minh tiếp tuyến tại $H,N$ của $\odot (BIC), BC$ và $AG$ đồng quy.

Trước tiên dễ thấy $BNCH$ điều hòa nên tiếp tuyến tại $N, P$ và $BC$ đồng quy.

Dễ chứng minh $AG', GD$ và $BC$ đồng quy

$\Rightarrow G$ là cực của đường thằng $AG$ với $\odot (BIC)$ mà $\overline{N,L,H}$ nên tiếp tuyến tại $N,H$ và $AG$ đồng quy. 

Vậy $4$ đường thẳng $AG, BC,$ tiếp tuyến tại $N$ và $H$ của $\odot (BIC)$ đồng quy tại điểm $J.$

Ta có: $JH^{2}= JB.JC= JA.JG= JP.JQ$ nên $JH$ cũng là tiếp tuyến của đường tròn $\odot (MPHQ)$ 

Vậy $\odot (BIC)$ và $\odot (MPHQ)$ có chung tiếp tuyến $JH$ nên $\odot (BIC)$ tiếp xúc $\odot (MPQ)$.

Ta có điều phải chứng minh.

Cho tam giác $ABC$ nhọn. đường tròn $(K)$ qua $B$ và $C$ cắt $AC$ và $AB$ tại $E$ và $F.BE$ cắt $CF$ tại $G.AG$ cắt $BC$ tại $P$. Hạ $PH$ vuông góc $EF$. Đường tròn ngoại tiếp tam giác $KEF$ cắt đường trung trực $BC$ tại điểm thứ $2$ là $I$. Chứng minh $AH$ và $AI$ là $2$ đường đẳng giác $\angle A$. 

Mình cũng sử dụng bổ đề $2$ của bạn, mình chứng minh nó bằng phép vị tự. 

Kẻ đường kính $AM$. 

Để ý nếu đường tròn ngoại tiếp tam giác $AEF$ cắt $\odot (O)$ tại điểm $X$ thì theo bổ đề $2$: $X,K,I,M$ thẳng hàng tức là $XM,EF$ cắt nhau tại $K$. 

Lấy $I'$ đối xứng với $I$ qua $EF$ thì $I'$ là trực tâm tam giác $AEF$.

Áp dụng định lí về điểm $Anti steiner$ dễ chứng minh được $X$ chính là điểm $Anti steiner$ đối với đường thẳng $HI'$ của tam giác $AEF$ nên $HI',EF$ và $XM$ từ đó nhận thấy $HI',EF$ và $XM$ đồng quy tại $K$. 

Do 2 đường thẳng $HI'$ và $XM$ đối xứng nhau qua $EF$ (theo $Anti steiner$) nên $KD $là phân giác $\angle IKH$

Bài toán được chứng minh.

Kẻ đường kính $BB'$ và $CC'$, sau đó áp dụng định lí $Pascal$. 

Gọi $N$ là trung điểm $AB$. Ta chứng minh $EF$ là đường đối trung của tam giác $EAB$.

Thật vậy dễ dàng chứng minh được $AP$ và $BQ$ là hai tiếp tuyến cắt nhau tại $F$ nên $EF$ là đường đối trung của tam giác $EAB$.

Vậy $EF$ đi qua trung điểm $CD.\blacksquare$

Cho tam giác $ABC$ có $I$ là tâm nội tiếp. $(I)$ tiếp xúc với $BC,CA,AB$ tại $D,E,F.$ Hạ $DK\perp EF$ và $H$ là trực tâm tam giác $ABC$.

Chứng minh $KD$ là phân giác $\angle IKH$.

Mình sử dụng $Anti steiner$ và vị tự nhưng thấy khá phức tạp! Mọi người ai có ý kiến gì thì đóng góp nhé!

giai thich cho minh cho nay dc k

Gọi $A_1$ là phần tử có nhiều nhất trong $64$ tập con và $a_1$ là số tập con chứa $A_1$, ta có:

$a_1\geq \frac{64.1008}{2016}=32$

Bài này mình giải ra nhưng mà kết quả lại sai, mình cũng ko biết sai chỗ nào hết. Mong các bạn giúp đỡ!

Bài 1 : Cho $x, y, z$ là các số thỏa mãn $(x + 1)^2 + (y + 2)^2 + (z + 3)^2 \leq 2010$. Tìm GTNN của biểu thức $P = xy + y(z - 1) + z(x - 2)$

Bài 2 : Cho $a, b, c, d, e > 0$ thỏa mãn điều kiện $a + b + c + d + e = 4$. Tìm GTNN của biểu thức $P = \frac{(a + b + c + d)(a + b + c)(a + b)}{abcde}$