Dãy số 5: $\left\{ {2,5,10,17,25,34,45,58} \right\}$
Em xin được giải thử ạ:
$\left\{ \begin{array}{l}
{u_{n + 1}} = {u_n} + 2n + 1\,\,\,\,(n \ne 4k) \\
{u_{n + 1}} = {u_n} + 2n\,\,\,\,(n = 4k) \\
\end{array} \right.$

Hi, chỗ đó bạn không hiểu là phải vì nó sai mà @_@. Chỗ đó phải là $-17^{n+1} + 16(17a - 1 + 17b +1)$ luôn chia hết cho 17. Vậy ta có thêm một cách nữa. Cách của bạn cũng thật là hay. Nó rất ngắn gọn.
http://mp3.zing.vn/b...u/ZWZDZI86.html

Cách 1: Áp dụng kiến thức về đồng dư: Khi a - b chia hết cho m ta có a và b đồng dư với nhau theo mod m, kí hiệu $a \equiv b\,(\bmod \,m)$.
Nếu $a \equiv b\,(\bmod \,m)$ và $c \equiv d\,(\bmod \,m)$ thì a + c và b + d đồng dư với nhau theo mod m.
Ta có 16 đồng dư - 1 theo mod 17 nên ${16^n} - 1 \equiv {( - 1)^n} - 1\, \equiv \,0(\bmod \,17) \Leftrightarrow {( - 1)^n} = 1$ hay khi và chỉ khi n chẵn.
Cách 2: Áp dụng định lí nhỏ Phéc - ma: Nếu (a, p) = 1 thì ${a^{p-1}} \equiv 1(\bmod \,p)$ với p là số nguyên tố.
Cách chứng minh định lí nhỏ này chỉ cần áp dụng cách hiểu về hệ thặng dư không đầy đủ mod p:
Với (a, p) = 1 ta có: $a.2a.3a...(p - 1)a \equiv 1.2.3...(p - 1)(\bmod \,p) \Rightarrow {a^{p - 1}} \equiv 1(\bmod p)$
Và kết hợp với kiến thức về đồng dư.
Theo Phéc - ma nhỏ ta có: $16^{16} \equiv 1 (mod 17)$
Ta xét 2 trường hợp:
- Trường hợp 1: n < 16 thử trực tiếp ta có kết quả là chỉ khi n chẵn thì mới có ${16^n} - 1$ chia hết cho 17.
- Trường hợp 2: Nếu n lớn hơn hoặc bằng 16 thi ta chia n cho 16 và khi đó ta sẽ có: n = 16a + r với $0 \le r < 16$ và ${16^n} - 1 \equiv {16^r} - 1\, \equiv \,0

(\bmod \,17)$. Quay về trường hợp 1, đó là thử trực tiếp cho r lần lượt bằng 0, 1, 2, ..., 15. Khi đó chỉ có r chẵn thì mới có ${16^n} - 1$ chia hết cho 17.
Tóm lại: ${16^n} - 1$ chia hết cho 17 khi và chỉ khi n chẵn.
-------------------------------------------------------------------
Vấn đề mở của ConanTM đặt ra cho bạn:
Áp dụng định nghĩa : a chia hết cho b khác 0 khi a = b.q.
Ta xét 2 trường hợp:
- Trường hợp 1: n lẻ. Biến đổi ta có:
${16^n} - 1={16^n} + 1 - 2=17a - 2$, rõ ràng không chia hết cho 17 (chia cho 17 dư 15).
- Trường hợp 2: n chẵn. Biến đổi ta có:
${16^n} - 1=-{17^{n+1}}+{16^n} + {17^{n+1}} - 1=-{17^{n+1}}+16(17a - 2+17b+1)=17m-16$ => ${16^n} - 1$ không chia hết cho 17???????????
Tại sao trong trường hợp này với cách làm như trên ta lại có khẳng định ngược lại? Sai lầm ở đâu?
http://www.nhaccuatu...?L=ec1cxBTECUyo

Bài toán 7: CMR: với mọi số tự nhiên n, biểu thức $16^{n}-1$ chia hết cho 7 khi và chỉ khi n là số chẵn. (Giải bằng nhiều cách).
Bài hát 7: http://mp3.zing.vn/b...t/ZW6WE97Z.html

Đề sai rồi anh chị ạ. Với n = 2 ta có điều vô lí.
http://mp3.zing.vn/b...t/ZW6WE98O.html

Lời giải khác của toán thủ ConanTM:
Bổ đề (*): Cho tam giác ONP, các điểm S, R, Q lần lượt thuộc các cạnh ON, NP, PO sao cho SR // PO và RQ // NO.
Khi đó ta có: ${S_{{\rm{OS}}RQ}} \le \frac{1}{2}S$ (Đây chính là bài toán B ở trên)

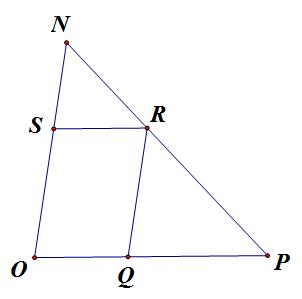
Chứng minh:
Đặt: $\frac{{NS}}{{NO}} = \frac{{NR}}{{NP}} = x \Rightarrow \frac{{PR}}{{PN}} = 1 - x$
Vì $\Delta NSR \sim \Delta NOP \sim \Delta RQP(gg) \Rightarrow \frac{{{S_{NSR}}}}{{{S_{NOP}}}} = {x^2};\frac{{{S_{RQP}}}}{{{S_{NOP}}}} ={(1 - x)^2}$
Và do đó: $\Delta NSR \sim \Delta NOP \sim \Delta RQP(gg) \Rightarrow {S_{{\rm{OS}}RQ}} = {S_{NOP}}{\rm{[}}1 - {x^2} - {(1 - x)^2}{\rm{]}} \le
\frac{1}{2}{S_{NOP}}.$ (đpcm)
Trở lại bài toán MSS:

Gọi I là giao điểm của XW và MN, MG // NJ // YZ với G, J thuộc XW. Đặt: $\frac{{XM}}{{XY}} = x;\frac{{XN}}{{XZ}} = y.$
Không mất tính tổng quát giả sử $x \le y$.
Ta xét 2 trường hợp:
- Trường hợp 1: $IM \ge IN$. Khi đó trên tia IM ta lấy điểm L sao cho IL = IN và kẻ LK // NJ với K thuộc XW =>${S_{{\rm{INJ}}}} = {S_{ILK}} \le {S_
{IMG}}$. Khi đó áp dụng bổ đề (*) ta có:
${S_{{\rm{MNPQ}}}} \le {S_{MGWQ}} + {S_{NJWP}} \le \frac{1}{2}({S_{XYW}} + {S_{XZW}}) \le M{\rm{ax}}\left\{ {{S_{XYW}};{S_{XZW}}}
\right\}$ (đpcm)
- Trường hợp 2: IM < IN. Với trường hợp này thì em giải giống hệt như trong lời giải đầu tiên vì em chưa tìm được lời giải nào đơn giản hơn ạ.
Tóm lại bài toán được giải hoàn toàn với cách nhìn đơn giản hơn như trong TH 1.
P/S: Liệu BT có cách giải đơn giản hơn mà không cần dùng tới bổ đề trong lời giải đầu tiên? (Các anh chị giúp em trả lời câu hỏi này với ạ vì em đã suy nghĩ nhiều mà chưa ra được đáp án).

Vấn đề mở thứ hai của toán thủ ConanTM:
Em có 1 phát hiện là bài toán MSS hình học trận 10 này chỉ là một mở rộng của bài toán sau:
Bài toán A:
Cho hình bình hành MNPQ nội tiếp tam giác XYZ với M, N, P, Q lần lượt thuộc các cạnh XY, XZ, YZ, YZ.
Chứng minh rằng:
${S_{PQMN}} \le \frac{1}{2}{S_{XYZ}}$

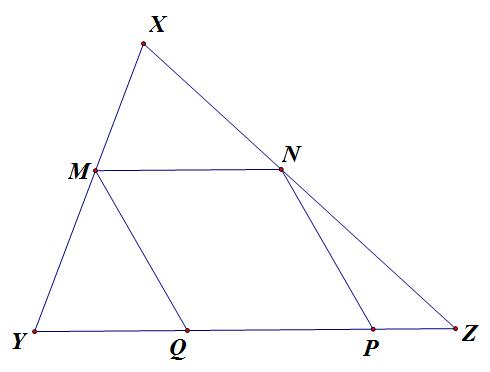
Và bài toán A lại chỉ là một mở rộng của bài toán sau:
Bài toán B:
Cho tam giác ABC, điểm D thuộc cạnh BC. Kẻ DE // AB và DF // AC với E, F lần lượt thuộc AC, AB.
CMR: ${S_{DEAF}} \le \frac{1}{2}{S_{ABC}}$

Các bài toán trên em thấy chứng minh khá là đơn giản và cũng rất hay nên em không nói lại ở đây và em cũng nhận thấy là trong bài toán MSS lần này nếu ta chứng minh được:
${S_{MNPQ}} \le \frac{1}{2}{S_{XYZ}}$ thì bài toán cũng sẽ được giải quyết. Câu hỏi em tự đặt ra là ta có thể vận dụng phép chứng minh bài toán A, bài toán B vào giải bài toán MSS lần này được không? Em mong các anh chị trên diễn đàn trả lời giúp em với ạ.

Mở rộng 4 của toán thủ ConanTM:

Cho tam giác RYZ, các điểm X, M, N, W lần lượt thuộc các đoạn thẳng RZ, XY, XZ, YZ. Kẻ MQ // XW // NP với P, Q thuộc cạnh YZ. Khi đó bằng những lập luận tương tự như trong lời giải bài toán ở trên ta có kết quả:
${S_{PQMN}} \le M{\rm{ax}}\left\{ {{S_{XYW}};{S_{XZW}}} \right\} \le M{\rm{ax}}\left\{ {{S_{RYW}};{S_{RZW}}} \right\}$
Với chú ý là: ${S_{RXW}} \le S_{RXY}$

Vấn đề mở thứ nhất của toán thủ ConanTM:
Cho hình thang XYZK (XK // YZ), các điểm M, N, W lần lượt thuộc các đoạn thẳng XY, XZ, YZ. Kẻ MQ // XW // NP với P, Q thuộc cạnh YZ. Vấn đề mở mà em đặt ra ở đây là hãy tìm quỹ tích các điểm T thỏa mãn:
${S_{PQMN}} \le M{\rm{ax}}\left\{ {{S_{TYW}};{S_{TZW}}} \right\} $
Với kết quả có được trong mở rộng 3 ta đã chứng minh được phần đảo của bài toán này, đó là T là điểm bất kì thuộc nửa mặt phẳng bờ XK không chứa hình thang, tuy nhiên còn phần thuận của BT thì em thấy sao mà khó thế ạ. Em mong các anh/ chị trên diễn đàn giải quyết giúp em với ạ.

Mở rộng 3 của toán thủ ConanTM:

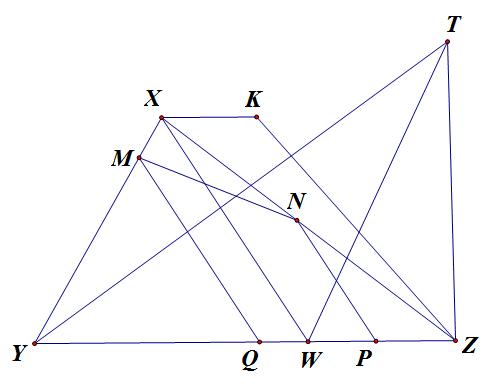
Cho hình thang XYZK (XK // YZ), các điểm M, N, W lần lượt thuộc các đoạn thẳng XY, XZ, YZ và T là điểm bất kì thuộc nửa mặt phẳng bờ XK không chứa hình thang. Kẻ MQ // XW // NP với P, Q thuộc cạnh YZ. Khi đó bằng những lập luận tương tự như trong lời giải ở trên ta cũng có khẳng định:
${S_{PQMN}} \le M{\rm{ax}}\left\{ {{S_{XYW}};{S_{XZW}}} \right\} \le M{\rm{ax}}\left\{ {{S_{TYW}};{S_{TZW}}} \right\} $

Mở rộng 2 của toán thủ ConanTM:

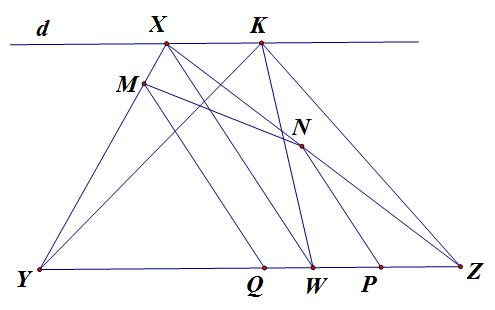
Cho tam giác XYZ, các điểm M, N lần lượt thuộc cạnh XY, XZ. W là điểm thuộc cạnh YZ và K là điểm bất kì thuộc đường thẳng d qua X và d // YZ.
Kẻ MQ // XW // NP với P, Q thuộc cạnh YZ. Khi đó bằng những lập luận tương tự như trong lời giải ở trên ta cũng có khẳng định:
${S_{PQMN}} \le M{\rm{ax}}\left\{ {{S_{KYW}};{S_{KZW}}} \right\} = M{\rm{ax}}\left\{ {{S_{XYW}};{S_{XZW}}} \right\} $

Mở rộng 1 của toán thủ ConanTM:


Cho tam giác XYZ, các điểm M, N lần lượt thuộc cạnh XY, XZ. J là điểm bất kì thuộc góc aXb là góc đối đỉnh với góc YXZ.
Kẻ MQ // JX // NP với P, Q thuộc cạnh YZ. Tia JX cắt cạnh YZ tại W. Khi đó bằng những lập luận tương tự như trong lời giải ở trên ta cũng có khẳng định:
${S_{PQMN}} \le M{\rm{ax}}\left\{ {{S_{XYW}};{S_{XZW}}} \right\} \le M{\rm{ax}}\left\{ {{S_{JYW}};{S_{JZW}}} \right\}$

Bài làm của toán thủ ConanTM:
Bổ đề: ${S_{ABC}} = \frac{1}{2}AB.AC.\sin \alpha $ với $\alpha = \widehat{\rm{A}}$ hoặc $\alpha = 180^0-\widehat{\rm{A}}$
Chứng minh:
Kẻ đường cao CH. Ta có: CH = $AC.\sin \widehat{\rm{A}} $ hoặc CH = $AC.\sin (180^0-\widehat{\rm{A}})$.
Do vậy: ${S_{ABC}} = \frac{1}{2}AB.CH=\frac{1}{2}AB.AC.\sin \alpha $ (đpcm)
Trở lại bài toán:

Đặt: $\frac{{XM}}{{XY}} = x;\frac{{XN}}{{XZ}} = y.$
Áp dụng bổ đề ta có: ${S_{XMN}} = xy{S_{XYZ}}$
Do MQ // XW // NP nên các cặp tam giác sau đồng dạng: YMQ và YXW; ZNP và ZXW.
Từ đó suy ra: ${S_{YMQ}} = {(1 - x)^2}{S_{XY{\rm{W}}}};{S_{YMQ}} = {(1 - y)^2}{S_{XZ{\rm{W}}}}$ (vì tỉ số diện tích của 2 tam giác đồng dạng
bằng bình phương tỉ số đồng dạng).
Do đó: ${S_{PQMN}} = {S_{XYZ}} - {(1 - x)^2}{S_{XY{\rm{W}}}} - {(1 - y)^2}{S_{XZ{\rm{W}}}} - xy{S_{XYZ}} \le M{\rm{ax}}\left\{ {{S_
{XYW}},{S_{XZW}}} \right\}\left[ {1 - {{(x + y - 1)}^2}} \right].$
=> ${S_{PQMN}} \le M{\rm{ax}}\left\{ {{S_{XYW}},{S_{XZW}}} \right\}.$ (đpcm)
Dấu "=" xảy ra <=> x + y =1 và W là trung điểm của YZ.
====
Trong các trận đấu trước thì bài làm của bạn mình thấy luôn có cách giải ngắn gọn và độc đáo nhất, mở rộng cũng nhiều và còn các câu hỏi mở xung quanh nó nhưng ở mở rộng lần này thì mở rộng 3 và 4 khá giống nhau nên mình không tính (bạn giải thích cho caybutbixanh đoạn bạn ấy hỏi nhé).
====
Điểm bài làm: 10
Tổng điểm: $S = \left [\frac{52 - \left (26 - 5 \right )}{2} \right ]+3*10+20+10=75$

Lời giải khác của toán thủ ConanTM:
Giả sử $a^2-a-b^2$ là số chính phương.
Do a + b chia hết cho 2 nên a và b cùng tính chẵn lẻ => $a^2-b^2$ chia hết cho 4. Do 1 số chính phương chia 4 chỉ dư 0 hoặc 1 nên a chia 4 dư 0 hoặc 3. Nếu a chia 4 dư 3 thì b lẻ, mặt khác khi đó a(a - 1) chia hết cho 8 và bằng tổng 2 số chính phương nên b chẵn vì 1 số chính phương khi chia 8 chỉ dư 0 hoặc 1 hoặc 4 (vô lý). Vậy a chia hết cho 4 => b chẵn.
Đặt a = 4m và b = 2n. Khi đó: $4m^2-m-n^2 = 4m^2-2m-n^2+m$ là 1 số chính phương => m chẵn vì hiệu 2 số chính phương là 1 số chẵn => a chia hết cho 8 => b chia hết cho 8.
Lại đặt a = 8m và b = 8n.
Ta có: $m(8m - 1) = 8n^2 + 8p^2$ với p là số tự nhiên => m chia hết cho 8 vì 8m - 1 là số lẻ => a chia hết cho 64
Lại đặt a = 64m và b = 8n. Ta có: $(8m)^2-8m-n^2 $ là số chính phương => n chia hết cho 8.
Cứ lặp lại như vậy thì ta có a và b phải có dạng $a = 2^x,b=2^y(x>2y>3)$ để $a^2-a-b^2$ là số chính phương hay $2^{2x}-2^x-2^{2y}$ là số chính phương => $2^{2(x-y)}-2^{x-2y}-1$ là số chính phương (Vô lý vì chia 4 dư 3). Vậy $a^2-a-b^2$ không thể là số chính phương (đpcm).

Lời giải của toán thủ ConanTM:
Đặt: S(a) = $a^2-a-b^2$. Giả sử S(a) là số chính phương thì S(1-a) cũng là số chính phương mà a và 1 - a khác tính chẵn lẻ => Mâu thuẫn vì theo giả thiết thì a và b phải cùng tính chẵn lẻ. (đpcm)
=================================
Mở rộng 1 của toán thủ ConanTM:
Với a + b chia hết cho 2 thì ta cũng có $(a+m)^2-(a+m)-b^2$ (với m nguyên dương) không là số chính phương vì nếu S(a+m) là số chính phương thì ta cũng có S[1-(a+m)] cũng là số chính phương mà a + m và 1 - (a + m) khác tính chẵn lẻ => mâu thuẫn.
Mở rộng 2 của toán thủ ConanTM:
Với a + b chia hết cho 2 thì ta cũng có $(ma)^2-ma-b^2$ (với m nguyên dương) không là số chính phương vì nếu S(am) là số chính phương thì ta cũng có S[1-(am)] cũng là số chính phương mà a m và 1 - (a m) khác tính chẵn lẻ => mâu thuẫn.
Mở rộng 3 của toán thủ ConanTM:
Với a + b chia hết cho 2 thì ta cũng có $(na+m)^2-(na+m)-b^2$ (với m, n nguyên dương) không là số chính phương vì nếu S(na+m) là số chính phương thì ta cũng có S[1-(na+m)] cũng là số chính phương mà na + m và 1 - (na + m) khác tính chẵn lẻ => mâu thuẫn.
----
Điểm bài làm: 10
Tổng điểm: $\left [ \dfrac{52-\left ( 23-19 \right )}{2} \right ]+3.10+3.10+10=94$

Đề bài trận 9 MSS của toán thủ ConanTM:
Giải phương trình nghiệm nguyên dương: $(x + 1)x^3=(5y+1)(5y-1) $
Đáp án:
Phương trình đã cho được viết lại như sau: $x^4+x^3+1=(5y)^2$
Ta sẽ đi tìm x nguyên dương để $x^4+x^3+1$ là một số chính phương.
Do $x^4+x^3+1>(x^2)^2$ nên $x^4+x^3+1=(x^2+a)^2$ với a là 1 số nguyên dương nào đó => $x^2(x-2a)=a^2-1$ => $a^2-1$ chia hết cho $x^2$=> $a^2-1$ = 0 hoặc $x^2\leq a^2-1$. Do vậy:
- Nếu $a^2$ = 1 thì a = 1 => Ta tìm được x = 2 và y = 1 là 1 nghiệm của phương trình đã cho.
- Nếu $a \neq 1$ thì do $a^2>a^2-1$ nên a > x => $x^2(x-2a)=a^2-1<0$ (mâu thuẫn) => trong trường hợp này phương trình đã cho vô nghiệm.
Vậy: PT đã cho chỉ có duy nhất 1 nghiệm nguyên dương (x,y) = (2,1).

Ta có trong 50 số hạng đầu tiên của dãy thì phải có 9 số 2 và 41 số 3. Do vậy tổng 50 số hạng đầu tiên của dãy bằng 9.2 + 41.3 =18 + 123 = 141.
http://www.nhaccuatu...?M=mukWL3HBSmZm

Ta có: $\Delta HFB = \Delta GCF(cgc) \Rightarrow FB = FC$ (1)
Hạ DI, AJ, FK, EL vuông góc với BC.
Khi đó ta cũng có: $\Delta DIB = \Delta BJA,\Delta ELC = \Delta AJC$ (Cạnh huyền-góc nhọn)=>DI = BJ, EL = CJ (2 cạnh tương ứng) kết hợp với FK là đường trung bình của hình thang DILE ta có: $FK = \frac{1}{2}(DI + EL) = \frac{1}{2}BC$ => Tam giác FBC vuông tại F (2). Từ (1) và (2) suy ra đpcm.

Lời giải của toán thủ ConanTM:

Không mất tính tổng quát giả sử độ dài cạnh của hình vuông ABCD bằng 1. Khi đó: BE = k và DF =$\frac{1-k}{1+k}$. Trên tia đối của tia BC lấy điểm M sao cho BM = DF. Ta có 2 tam giác vuông ADF và ABM bằng nhau (cgc) => AF = AM. Ngoài ra ta cũng có:
EM = EB + BM = BE + DF = $\frac{1+k^2}{1+k}$.
FE = $\sqrt{CF^2+CE^2} $(theo định lí Pitago cho tam giác vuông)
=> FE =$\sqrt{(1-DF)^2+(1-BE)^2}=\sqrt{(1-k)^2+\left ( \frac{2k}{1+k} \right )^2}=\frac{1+k^2}{1+k}$. => FE = EM.
Do vậy $\Delta AEF =\Delta AEM (ccc)\Rightarrow AN = AB$ (2 đường cao tương ứng).
Vì thế cho nên:
$\Delta ADF =\Delta ANF$(cạnh huyền - cạnh góc vuông)$ \Rightarrow \widehat{DAF} = \widehat{NAF}$ ( 2 góc tương ứng),
$\Delta ABE =\Delta ANE$(cạnh huyền - cạnh góc vuông)$ \Rightarrow \widehat{BAE} = \widehat{NAE}$ ( 2 góc tương ứng).
Áp dụng tính chất đường phân giác trong tam giác cho các tam giác ADP và ABP ta có: $\frac{PG}{DG}=\frac{AP}{AD}=AP;\frac{PH}{BH}=\frac{AP}{AB}=AP\Rightarrow \frac{PG}{DG}=\frac{PH}{BH}(=AP)\Rightarrow \frac{PG}{PH}=\frac{DG}{BH}$ (đpcm).
====
Khác với cách giải khác, cách này sử dụng phương pháp "đặc biệt hóa" nên không phải xài các bổ đề phụ nào cả , nói chung là hay .
Điểm bài làm: 10.
Tổng điểm: 33+3.10+0+10=73

Trước tiên, em thấy là các anh doavuquang và BlackSelena đã có thái độ không đúng lúc đối với trọng tài và em cũng thấy được là các trọng tài MSS khi chấm điểm đã có thái độ động viên và khích lệ rất nhiều dành cho các toán thủ MSS nói chung và với em nói riêng, điều đó có thể không chính xác nhưng là cần thiết ít ra là với 1 HS THCS như em, hiểu biết còn nhiều hạn chế và em cũng thấy là mọi người tham gia giải bài thi MSS đều rất giỏi, em học hỏi được rất nhiều từ các anh chị trên diễn đàn này. Vì tuổi còn nhỏ nên em thấy em thật là dốt khi đưa ra những nhận xét như vậy. Hơn nữa nhiều chỗ kiến thức em cũng thấy em còn dốt lắm. Em mong được học hỏi từ các anh chị nhiều ạ.

Ban đầu em cũng định kết luận nghiệm như anh daovuquang nhưng em đã nghĩ lại vì thấy nó thật sự không ổn, để em nói rõ hơn: Ví dụ: bộ số $(x_1;x_2;...;x_{2012})=(\frac{-1+\sqrt{5}}{2};0;\sqrt{5};0;...;0,-\sqrt{5},0;...,\sqrt{5},\frac{-1+\sqrt{5}}{2})$ cũng thỏa mãn các điều kiên trong KL về nghiệm của anh nhưng không là nghiệm của HPT.

Bài làm của daovquang:
Viết lại hệ pt: $$\left\{\begin{matrix} x_{1}+x_{2}+...+x_{2012}=-1\; (1) & \\ x_{1}\left ( x_{2}+x_{3}+...+x_{2012} \right )=-1\; (2) & \\ \left ( x_{1}+x_{2} \right )\left ( x_{3}+...+x_{2012} \right )=-1 & \\ .......... & \\ \left ( x_{1}+x_{2}+x_{3}+...+x_{2011} \right )x_{2012}=-1 & \end{matrix}\right. $$

Từ $(1)\Rightarrow x_2+...+x_{2012}=-1-x_1$.
Thay vào $(2)$, ta được : $x_1(-1-x_1)=-1$
$\Leftrightarrow x_1^2+x_1-1=0$
$\Leftrightarrow x_1=\frac{-1 \pm \sqrt{5}}{2}$.
Tương tự, $x_{2012}=\frac{-1 \pm \sqrt{5}}{2}$.
Mặt khác, xét $(x_1+...+x_{k-1})(x_k+x_{k+1}+...+x_{2012})=(x_1+...+x_{k-1}+x_k)(x_{k+1}+...+x_{2012})\; (k \in \mathbb{N}^*; 2\le k\le 2011)$
$\Leftrightarrow (x_1+...+x_{k-1})x_k+(x_1+...+x_{k-1})(x_{k+1}+...+x_{2012})=(x_1+...+x_{k-1})(x_{k+1}+...+x_{2012})+x_k(x_{k+1}+...+x_{2012})$
$\Leftrightarrow x_k[(x_1+...+x_{k-1})-(x_{k+1}+...+x_{2012})]=0$
$\Leftrightarrow x_k=0$ hoặc $x_1+...+x_{k-1}=x_{k+1}+...+x_{2012} (*)$.
Đặt $x_1+...+x_{k-1}=a$.
Thay $(*)$ vào $(1)\Rightarrow 2a+x_k=-1 \Leftrightarrow a=\frac{-1-x_k}{2}.$
Khi đó $(x_1+...+x_{k-1})(x_k+x_{k+1}+...+x_{2012})=-1$
$\Leftrightarrow a(x_k+a)=-1$
$\Leftrightarrow \frac{-1-x_k}{2}(x_k+\frac{-1-x_k}{2})=-1$
$\Leftrightarrow 5-x_k^2=0$
$\Leftrightarrow x_k=\pm \sqrt{5}$ với $k=2;3;...;2011$
$\Rightarrow x_k=0$ hoặc $x_k=\pm \sqrt{5}$ với $k=2;3;...;2011$.
Kết luận: phương trình có nghiệm $x_1=x_{2012}=\frac{-1 \pm \sqrt{5}}{2}$; $x_k=0$ hoặc $x_k=\pm \sqrt{5}$ với $k=2;3;...;2011$ thỏa mãn $x_2+x_3+...+x_{2011}=0$ hoặc $\pm \sqrt{5}$.

Xin lỗi vì anh học lớp 9 hơn em 1 lớp nhưng từ $x_1=x_{2012}=\frac{-1 \pm \sqrt{5}}{2}$ mà anh lại có $x_2+x_3+...+x_{2011}=0$ thì hoàn toàn là sai lầm anh ạ.

Mình không thi nhưng vẫn xin gửi lời giải của mình lên, lời giải này mình sử dụng kiến thức về hệ thức Viète của lớp 9 để giải.
Đặt $u_1=x_1$ và $v_1=\sum x_i$ với $i=\overline{2;2012}$. Khi đó từ phương trình $(1)$ và phương trình $(2)$ của hệ ta được:
$\left\{\begin{matrix} u_1+v_1=-1 & \\ u_1v_1=-1 & \end{matrix}\right. $
Do đó theo hệ thức Viète $u_1$ và $v_1$ là nghiệm của phương trình: $t^2+t-1=0$.
Giải phương trình trên ta được $u_1=x_1=\dfrac{1}{2}\left ( -1+\sqrt{5} \right )$, $v_1=\dfrac{1}{2}\left ( -1-\sqrt{5} \right )$ hoặc $v_1=\dfrac{1}{2}\left ( -1-\sqrt{5} \right )$, $v_1=x_1=\dfrac{1}{2}\left ( -1+\sqrt{5} \right )$.
Tiếp tục đặt $u_2=x_1+x_2$ và $v_2=\sum x_i$ với $i=\overline{3;2012}$ thì ta có hệ:
$\left\{\begin{matrix} u_2+v_2=-1 & \\ u_2v_2=-1 & \end{matrix}\right. $
Do đó $u_2=\dfrac{1}{2}\left ( -1+\sqrt{5} \right )$ hoặc $u_2=\dfrac{1}{2}\left ( -1-\sqrt{5} \right )$.
Từ đó suy ra $x_2=0$ hoặc $x_2=-1-2x^1$.
Tiếp tục đặt $u_3=x_1+x_2+x_3$ và $v_3=\sum x_i$ với $i=\overline{4;2012}$ thì ta có hệ:
$\left\{\begin{matrix} u_3+v_3=-1 & \\ u_3v_3=-1 & \end{matrix}\right. $
Do đó $u_3=\dfrac{1}{2}\left ( -1+\sqrt{5} \right )$ hoặc $u_3=\dfrac{1}{2}\left ( -1-\sqrt{5} \right )$.
Từ đó suy ra $x_3=0$ hoặc $x_3=-x_2$.
Tiếp tục quá trình trên ta được: $x_2=x_4=...=x_{2012}$ và $x_3=x_5=...=x_{2011}$ và các giá trị của nghiệm ta đã tìm được như trên là $0$ hoặc $\sqrt{5}$ hoặc $-\sqrt{5}$.

Lời giải của anh/ chị bỏ sót cả mấy ngàn nghiệm. KL $x_2=x_4=...=x_{2012}$ là sai hoàn toàn.

Em thấy rằng đề bài lần này mang tính trình bày rất cao, có thể nói rằng các lời giải của các bạn khác đều sai hoặc thiếu rất nhiều vì chưa tính đến vị trí các nghiệm $x_2,x_3,...,x_{2011}$. Cái này gần như quyết định tính đúng sai trong lời giải bài toán. Như vậy có thể thấy lời giải của daovuquang và BlackSelena chỉ đúng 1 phần nhỏ vì bỏ sót rất nhiều nghiệm. Thậm chí KL về nghiệm của daovuquang hoàn toàn chưa chính xác.

Em xin được sửa và bổ sung thêm như sau vì có 1 số chỗ thiếu sót:
Em xin thay đoạn:
$\left[ \begin{array}{l}
{x_2},{x_3},...,{x_{2011}} \in \left\{ {0; - \sqrt 5 } \right\} \\
{x_2},{x_3},...,{x_{2011}} \in \left\{ {0;\sqrt 5 } \right\} \\
\end{array} \right.$
và: $\left[ \begin{array}{l}
{x_2} + {x_3} + ... + {x_{2011}} \in \left\{ {0; - \sqrt 5 } \right\} \\
{x_2} + {x_3} + ... + {x_{2011}} \in \left\{ {0;\sqrt 5 } \right\} \\
\end{array} \right.$
bởi: ${x_2},{x_3},...,{x_{2011}} \in \left\{ {0; - \sqrt 5 ,\sqrt 5} \right\}.$
và: ${x_2}+{x_3}+...+{x_{2011}} \in \left\{ {0; - \sqrt 5 ,\sqrt 5} \right\}.$
Do đó em xin bổ sung thêm nhiều nghiệm nữa:
- Bộ nghiệm bổ sung thứ nhất (trong TH1):
$({x_1},{x_2},...,{x_{2012}}) \in \left\{ {(\frac{{ - 1 + \sqrt 5 }}{2},0,...,-\sqrt 5,0,...,\sqrt 5,...,-\sqrt 5,0,..,\sqrt 5,\frac{{ - 1 - \sqrt 5 }}{2});(\frac{{ - 1 - \sqrt5 }}{2},0,..,\sqrt 5,0,...,-\sqrt 5,...,0,..,\sqrt 5,0,...,-\sqrt 5,\frac{{ - 1 + \sqrt 5 }}{2})} \right\}$ với chú ý là các số 0 có thể có hoặc không, số lượng các số 0 phải là số chẵn.
- Bộ nghiệm bổ sung thứ hai (trong TH 2, 3):
$({x_1},{x_2},...,{x_{2012}}) \in \left\{ {(\frac{{ - 1 + \sqrt 5 }}{2},0,...,-\sqrt 5,0,...,\sqrt 5,...,-\sqrt 5,0,..,\frac{{ - 1 + \sqrt 5 }}{2});(\frac{{ - 1 - \sqrt 5 }}{2},0,..,\sqrt 5,0,...,-\sqrt 5,...,0,..,\sqrt 5,0,...,\frac{{ - 1 - \sqrt 5 }}{2})} \right\}$ với chú ý là các số 0 phải có thể, số lượng các số 0 phải là số lẻ.
=> HPT có thêm 2 bộ nghiệm nữa ở trên và các mở rộng với số ẩn là số chẵn (2n) thì đều được bổ sung thêm 2 bộ nghiệm được hiểu tương tự như ở trên. Còn trong mở rộng với số ẩn bất kì thì trong TH chẵn ẩn cũng được bổ sung thêm tương tự (như vậy là phải chia thành 2 khả năng có thể xảy ra là số ẩn chẵn và số ẩn lẻ).
Trên đây là 1 số bổ sung thêm vì chưa hết thời hạn gửi bài nên em nghĩ là được ạ.

Em đã có những suy nghĩ nhiều xung quanh bài toán này nhưng với hiểu biết còn rất hạn hẹp của em thì em thấy rằng em còn kém lắm ạ. Một số vấn đề rất tự nhiên em nghĩ đến nhưng thật sự là em không biết phải làm thế nào, mong các anh chị giải đáp dùm em với. Đó là:
Vấn đề 1: Giả sử rằng ta có dãy số $a_n$ có tính chất sau:
$\left\{ \begin{array}{l}
\sum\limits_{n = 1}^h {{a_n}} = - 1 \\
\left( {\sum\limits_{k = 1}^t {{a_k}} } \right)\left( {\sum\limits_{v = t + 1}^h {{a_v}} } \right) = - 1 \\
\end{array} \right.$
Liệu rằng ta có thể xác định được công thức tổng quát của dãy số $a_n$ hay không? Trong lời giải của em mặc dù em thấy rằng đã xuất hiện một chút manh mối về cái dãy $a_n$ nhưng vấn đề về dấu của các số hạng $a_k$ với k lần lượt chạy từ 2 cho đến h - 1 em thấy thật khó xác định, ngay cả trong trường hợp bằng 0 hay là không?
Vấn đề 2: Nếu em giả sử có đa thức f(x) có tính chất:
$\left\{ \begin{array}{l}
f(x) + f(y) = - 1 \\
f(x)f(y) = - 1 \\
\end{array} \right.$
Thì liệu rằng ta có thể xác định được đa thức f(x) hay không? Nếu thêm điều kiện gì thì vấn đề sẽ dễ giải quết hơn?
Em có đôi lời xin được bày tỏ ạ?