Tự nhiên lục lại thấy cái chuyên đề viết dở năm cấp 3, tặng anh em diễn đàn mình tham khảo (chỉ sợ nó lỗi thời rồi) , nếu bạn nào quan tâm thì liên hệ vs mình qua facebook mình sẽ gửi bản word và bạn tìm hiểu + giúp mình hoàn thành nốt phần còn lại nhé. 

Chứng minh của Sally trên sai ở ngay bước chứng minh hệ số $a_n$ dẫn đến kết luân nghiêm sai.

Dạng này có thể sử dụng số phức.

Dễ thấy nếu đa thức $x_0 \in R$ thì $P(x)$ cũng có nghiệm $x_0^2$ và $(x_0-2)^2$. Do vây nếu $\left | x_0 \right |\neq 1$ thì đa thức $P(x)$ có vô hạn nghiệm.

(Do nếu ngược lai thì $P(x)$ có các nghiệm $1<x_0<x_0^2<x_0^4<...$ hoặc $1>x_0>x_0^2>x_0^4>...>0$ đôi một phân biệt ,vô lí)

Suy ra $\left | x_0 \right |=1$ và $x_0=1$ (nếu $x_0=-1$ thì $P(x)$ có nghiệm $(x_0-2)^2=9>1$ vô lí) hay $P(x)=(x-1)^k.Q(x)$ với $Q(x)$ là đa thức hệ số thực không có nghiệm thực.

Dễ thấy thay vào phương trình $P(x)$ suy ra $Q(x)Q(x+2)=Q(x^2)$.  (1)

Giả sử $Q(x)$ có các nghiệm phức $\alpha _k=a_k+i.b_k$.Dễ thấy $\left |\alpha _k  \right |=1$ vì nếu ngược lại thì $Q(x)$ cũng có vô hạn nghiệm phức, vô lí.

Do đó $a_k^2+b_k^2=1$ (suy ra $a_k,b_k <1$, mặt khác theo (1) ta có Q(x) cũng có nghiệm $(\alpha _k -2)^2$.

Mà $\left |(\alpha _k -2)^2  \right |=(a_k-2)^2+b_k^2>1$ do $a_k<1 \Rightarrow  (a_k-2)^2>1$, vô lí vì mọi nghiệm của $Q(x)$ đều có modun là 1.

Suy ra $Q(x)=c$ hay $P(x)=c.(x-1)^k$, thay vào phương trình dễ thấy $c=0$ hoặc $c=1$.

Kết luận $P(x)=0$ hoặc $P(x)=(x-1)^k$ (k là số tự nhiên bất kì)

Em nhận được rồi thầy ạ

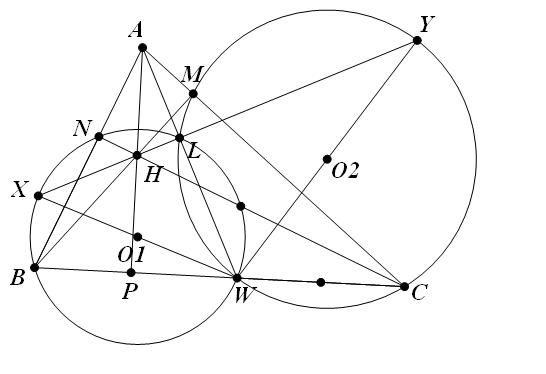
Bài 4 có cách phương tích 

Gọi $L,L'$ là giao điểm của $AW$ với các đường trong (1) và (2) .

Phương tích suy ra $AL.AW=AN.AB$,$AL'.AW=AM.AC$ mà $AN.AB=AM.AC$ nên $L=L'$ hay A,L,W thẳng hàng .

Do $XY$ sông song với $O_1O_2$ (đường trung bình) nên $XY$ vuông góc với $AW$.

Gọi $H'$ là giao điểm cuả đường cao $AP$ với $XY$ suy ra 2 tam giác $AH'L$ và $AWP$ đông dạng.

Suy ra: $AH'.AP=AL.AW=AN.AB$ mà $AN.AB=AH.AP$ hay $H'=H$. Suy ra $X,Y,H$ thẳng hàng.

 

 

Địa chỉ nhận GCN của em là : Lê Kim Bình, xóm 2 Bắc Lâm, Diễn Lâm, Diễn Châu, Nghệ An.

Lê Kim Nhã, lớp A1K40,THPT chuyên Phan Bội Châu,Nghệ An (giấy BTC gửi về trường cho em luôn ạ)

STK:51110000120258

CTK:Trường Thị Hà Trang

Ngân hàng BIDV TP Vinh,Nghệ An

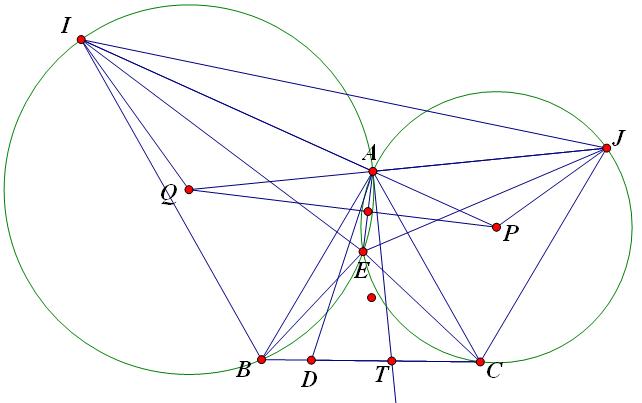
Gọi $Q,P$ lần lượt là tâm đường tròn ngoại tiếp $ABI,ACJ$.

Trước hết ta chứng minh $(Q,A,J);(P,A,I)$ là hai bộ điểm thẳng hàng.

   Gọi AT là phân giác $\angle CAD$, suy ra $AT\perp AJ$ (phân giác 2 góc bù nhau)

   Ta cần chứng minh $AT \perp AQ$ hay $AT$ là tiếp tuyến của $(Q)$, thật vậy ta có:

      $\angle AIB =180^{\circ}- \angle IAB -\angle IBA = 180^{\circ}-(90^{\circ}-\frac{ \angle SAD}{2} )-60^{\circ} = \frac{ \angle SAD}{2} + 30 ^{\circ}$

    $\angle BAT =60^{\circ}-\frac{ \angle CAD}{2}=\frac{ \angle SAD}{2} + 30 ^{\circ}$

  Do đó: $\angle AIB= \angle BAT $ hay $AT$ là tiếp tuyến của $(Q)$ suy ra $A,Q,J$ thẳng hàng.

  Tương tự ta cũng có $I,A,P$ thẳng hàng.

Trở lại bài toán ta sẽ chứng minh $JA$ là phân giác $\angle IJE$, thật vậy:

Ta có: $\angle ABI =\angle ACJ=60^{\circ} $ suy ra hai dây cung bị chắn $AI : AJ = R_{(Q)}:R_{(P)}$ hay  $\frac{AI}{AJ}=\frac{AQ}{AP}$

   Suy ra tứ giác $JIQP$ nội tiếp $\Rightarrow \angle IJA= \angle APQ$

   Xét đường tròn $(P)$ có $PQ$ vuông góc với dây $AE$ nên $\angle APQ =\angle AJE = 0,5.Sđ(\widehat{AE})$

  Suy ra : $\angle IJA= \angle APQ = \angle AJE$

Suy ra  $JA$ là phân giác $\angle IJE$

Tương tự $IA$ là phân giác $\angle JIE$

Vậy $A$ là tâm đường tròn nội tiếp tam giác $JIE$ (đpcm)

 

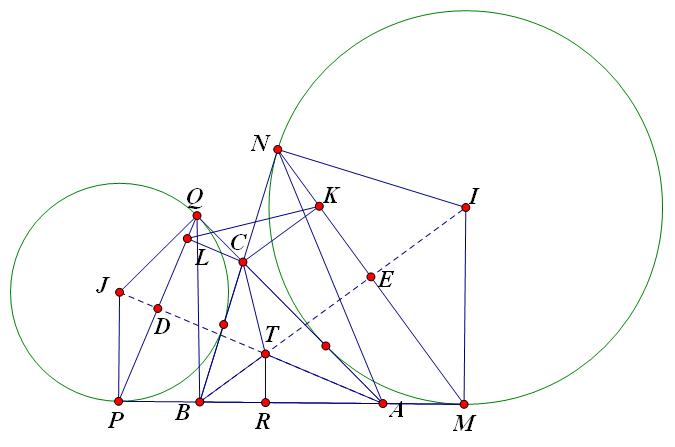
Bài 1.Gọi $T$ là tâm đường tròn nội tiếp tam giác $ABC$.

Ta sẽ chứng minh $\angle QLK = \angle KMP  \Rightarrow \angle CLK = \angle TBA$ (phụ nhau)

Hay ta sẽ chứng minh 2 tam giác $TAB$ và $CKL$ đồng dạng.

Thật vậy,

   $\frac {CL}{AD}= \frac{QC}{QA} ; \frac{CK}{BE} = \frac{NC}{NB}$ 

 $\Rightarrow \frac {CL}{CK} = \frac {AD.QC.NB} {BE.NC.QA}$

Ta lại có :

  $BI = \frac {BM^2}{BE};\frac {BT}{BI}= \frac {BR}{BM} \Rightarrow BT= \frac {BM.BR}{BE} =\frac {BN.QC}{BE}$

 Tương tự ta cũng có $AT= \frac {AP.AR}{AD} = \frac {AQ.CN}{AD} $

 Suy ra: $ \frac {BT}{AT} = \frac {BN.QC.AD} {BE.AQ.CN} = \frac{CL}{CK}$

Mặt khác hai cặp cạnh $\left ( TB,CK \right );\left ( TA;CL \right )$ song song nên $\angle LCK =\angle BTA $

Do đo 2 tam giác $CLK$ và $TBA$ đồng dạng. Ta có đpcm.

Bài 18.Sử dụng nội suyLagrange và đa thức Chebysev.

$T_{n-1}(x)=\sum_{k=0}^{n-1} T_{n-1}(x_k)\prod_{i\neq k}\frac{x-x_i}{x_k-x_i}$

Xét hệ số cao nhất ta có :

 $2^{n-2}=\sum_{k=0}^{n-1} \frac{T_{n-1}(x_k)}{\prod_{i\neq k}(x_k-x_i)}$

Suy ra 

$2^{n-2}\leq \left |\sum_{k=0}^{n-1} \frac{T_{n-1}(x_k)}{\prod_{i\neq k}(x_k-x_i)}  \right | \leq \sum_{k=0}^{n-1} \frac{1}{\left |\prod_{i\neq k}(x_k-x_i)  \right |}=S_n$

Ngày 2.

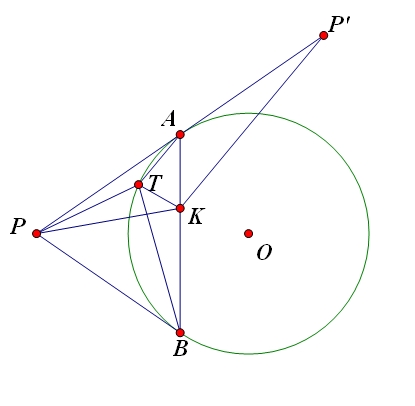
Bài 1.(hình vẽ)

   Dễ thấy $\angle PBT=\angle TAB;\angle ATB=\angle KAP'$.

   Do đó để chứng minh kết quả bài toán cần chứng minh $\Delta ATB\sim \Delta KAP'(c.g.c)$.

Thật vậy do $\angle ATB=\angle KAP'$ nên chỉ cần chứng minh

$$\frac{AK}{AT} = \frac{AP'}{TB} = \frac{BP}{BT}$$

Mà tứ giác $KTPB$ nội tiếp nên $ \angle TPB = \angle AKT $ và $\angle TAK= \angle TBP$ nên hai tam giác $TPB$ và $TAK$.

Suy ra : $\frac{AK}{AT} = \frac{BP}{BT}$ (đpcm)

Bài 2. Chú ý ta có thể đồng thời tăng giá trị ở mỗi hàng (cột ,đchéo) lên một số nguyên k bất kì (k có thể âm).

Bài 3.  $a_{n+2}=\left [ \frac{2a_n}{a_{n+1}} \right ]+\left [ \frac{2a_{n+1}}{a_n} \right ] $

Dễ thấy trong hai số nghịch đảo có 1 sô không nhỏ hơn 1 nên $a_n \geq 2$ với mọi n.

Và nếu có $a_{n}=a_{n+1}$ thì $a_{n+2}=4$

 

 Nếu có 1 số $a_n=2$ thì $a_{n+2}=a_{n+1} + \left [ \frac{4}{a_{n+1}} \right ]$.

   Khi đó 

              TH1. $a_{n+1}=3 \Rightarrow a_{n+2}=4;a_{n+3}=3$,t/m

              TH2.$a_{n+1}=4 \Rightarrow a_{n+3}=3;a_{n+4}=4;a_{n+5}=3$,t/m

              TH3. $a_{n+1}>5$ thì $a_{n+2}=a_{n+1}$ $ \Rightarrow$  $a_{n+3}=4$,tiếp tục xử lí như TH $a_n \geq 3$

 

 Nếu  $a_n \geq 3$ với mọi n thì

      TH1. Tồn tại $a_n<a_{n+1}$ suy ra $\left [ \frac{2a_{n+1}}{a_n} \right ] \leq a_{n+1}-1$ và $\left [ \frac{2a_n}{a_{n+1}} \right ] <1 $. 

        Do đó $a_{n+2} \leq a_{n+1}$ nên dãy có số hạng $a_{n+1}$ là lớn nhất.

   Hay ta có nhân xét là nếu tồn tại $a_n<a_{n+1}$ thì mộ số hạng phía sau $a_{n+1}$ đều không lớn hơn  $a_{n+1}$ và dương nên tồn tại một dãy vô hạn số hạng liên tiếp bằng nhau ( cùng = 4), t/m

       TH2. $a_{n} \geq a_{n+1}$ với mọi $n$ thì tồn tại một dãy có vô số số hạng liên tiếp cùng bằng nhau và bằng 4,t/m.

Như vậy ta có đpcm

 

 

Bài 16. Xét trên cả Radian và Degree ta đều có: $1 \geq cos(\alpha) \geq 0$ với mọi $0 \geq \alpha \geq 1$.

Suy ra: $0 \geq a_n \geq 1$.

Xét hàm số $f(x)=cosx$ trên $(0,1)$ ta có $f'(x)<0$ suy ra $a_{2k}$ và $a_{2k+1}$ là 2 dãy đơn điệu, mà dãy bị chạn nên tồn tại giới hạn của 2 dãy, giả sử là $A$ và $B$.Suy ra:

$A=cos(B)$

$B=cos(A)$

Suy ra: $A=cos(cosA)$, đến đây xét hàm $g(x)=x-cos(cosx)$ trên $(0,1)$ có đạo hàm lớn hơn 0 nên có nghiệm và duy nhất. Do đó $A=B$.Hay dãy đã cho có giới hạn hữu hạn

Bài 17. Em nghĩ là nếu có lời giải số học thì cũng chỉ là biến đổi và quy nạp thôi, và hiển nhiên thì nó tương đương với việc xét pt đặc trưng.

Bài 12''. Em đang nghĩ đến việc chuyển nó về một bài toán tổ hợp đếm rồi suy ra kết quả bằng cách tính khác.

Kiểu như là : Cho tập $k$ người thì $a_k$ sẽ bằng số cách chọn ra một nhóm người nào đó thõa mãn điều kiện T

                     Khi đó với tập $m$ người thì ta lại tiếp tục chọn thõa mãn tính chất T, khi đó ta sẽ tách tập $m$ người này thành các tập nhỏ và được kết quả $a_m$ chính bẳng tổng các tích nhỏ (số cách chọn ra k người từ m người)*(số cách chọn cho tập k người thõa mãn T) = $\sum (C_m^k.a_k)$

Bây giờ chỉ còn việc chọn T sao cho $a_0=2$ và tồn tại phép  tổng ở trên. 

Trong hình lồi F thì nó $=max\left \{ d(A,B) : A,B\in F\right \}$.

Đặc biệt trong đa giác thì đường kính là khoảng cách xa nhất giẵ hai đỉnh

Thì chúng ta còn 3 cạnh chưa bị phủ hết , nên nhất thiết 2 đường tròn còn lại phải phủ hết chúng. Mặt khác hai đường tròn còn lại nếu phủ các góc vuông thì chỉ phủ được nhiều nhất tổng độ dài các cạnh góc vuông là $4\sqrt{2}R$

Câu trả lời là không.

Ta sẽ chứng minh bài toán thông qua việc chứng minh chúng không phủ hết cạnh của hình vuông.(mấu chốt).

    Trước hết xét một $(O,R)$ và một góc vuông $Axy$ sao cho $(O,R)$ cắt hai cạnh của góc lần lượt tại $M;N$.

    Ta có: (Hình vẽ) $AM^2+AN^2=MN^2 \leq (2R)^2=4R^2$

    Mặt khác theo AM-GM thì $AM^2+AN^2 \geq \frac{(AM+AN)^2}{2}$

 $\Rightarrow AM+AN \leq 2\sqrt{2}R$.

Trở lại bài toán ban đầu, ta dựng các đường tròn bán kính $0,5$ có tâm là các đỉnh của hình vuông, suy ra 2 đường tròn bất kì trong số chúng có chung nhau nhiều nhất 1 đỉnh.

Mặt khác 3 đường tròn đã cho phủ hết 4 đỉnh nên mỗi đường tròn ta mới vẽ chứa ít nhất một tâm của các hình tròn đã cho.

Theo nguyên lí Dirichle (3 đường tròn ,4 điểm) thì tồn tại một tam là tiếp điểm của 2 đường tròn (trung điểm một cạnh).

Như vậy còn 3 cạnh hình vuông hoàn toàn chưa bị phủ (tổng độ dài của chúng là 3).

Mà chỉ còn 2 đường tròn nên theo nhận xét ban đâu thì chúng phủ nhiều nhất tổng độ dài $4\sqrt{2}R=2\sqrt{2}<3$  (Vô lí).

Vậy ta có đpcm.

 

Chứng minh trực tiếp: Ta chỉ cần chứng minh giao của tât cả đường tròn tâm đỉnh đa giác bán kính $\frac{d}{\sqrt{3}}$ khác rỗng.

 ta thấy Chỉ cần chứng minh cho tam giác , phần còn lại suy ra từ định lí Helly.

Xét tam giác ABC có độ dài 3 cạnh không lớn hơn $d$ (Khi đó đường kính của tam giác này không lớn hơn $d$ theo t/c đường kính của tam giác)

Nếu nhọn: Chọn tâm đường tròn nội tiếp. ( Chú ý gs AB lớn nhât thì $R=\frac{AB}{2sinC} \leq  \frac{d}{\sqrt{3}}$)

Nếu tù: Chọn tâm là trung điểm cạnh dài nhất . ( Chú ý $a^2+b^2<c^2$ nên $m_C = \sqrt{\frac{a^2+b^2}{2}-\frac{c^2}{4}}  \leq \frac{d}{\sqrt{3}}$)

Đây là một trong những hệ quả hệ quả của định lí sau: Cho hình lồi có đường kính $d$ ta luôn phủ được nó bởi một hình lục giác đều có khoảng cách giữa hai cạnh đối nhau là $d$. (Tạm thời mình quên mất tên đinh lí này, )

Áp dụng định lí này ta có ngay hình tròn bán kính $\frac{d}{\sqrt{3}}$ ngoại tiếp lục giác trên.

Chứng minh định lí trên ta sử dụng phương pháp tịnh tiến và quay các đường thẳng để tạo nên lục giác.Lời giải mình xin post sau....

Dựng các đường tròn $(A_i;0,5)$ với $i=\overline{1,2011}$ ($A_i$ là các điểm).

Theo giả thiết bài toán các đường tròn này đôi một không cắt nhau.

Xét một điểm $A_i$ bất kì, lấy 6 điểm gần $A_i$ nhất.

Xem hình vẽ ta thấy có nhiều nhất sau đường tròn có thể cùng tiếp xúc với $(A_i;0,5)$. Khi đó đường tròn thứ 7 gần $(A_i;0,5)$ nhất là đường tròn $(B;0,5)$ như hình vẽ.Dễ dàng tính được $A_iB=\sqrt{3}$.

Như vậy tất cả các điểm khác 6 điểm gần $A_i$ nhất đều cách $A_i$ một khoảng không bé hơn $\sqrt{3}$.

Ta thực hiện như sau: Lấy một điểm bất kì rồi xóa đi 6 điểm gần nó nhất, xét các điểm không bị xóa khác điểm vừa chọn ta lại xóa đi 6 điểm gần nó nhất (6 điểm này không chứa điểm đã chọn ở bước trước),..., thực hiện thuật toán cho đến khi kết thúc ta thu được $\left [ \frac{2011}{6} \right ]$ điểm đôi một cách nhau $\geq \sqrt{3}$. 

Gọi $a=d(M,d);k_i+b$ là độ dài đoạn $M'A_i$ với $k_i$ là các số nguyên.

Suy ra: $MA_i=\sqrt{a^2+(k_i+b)^2}=\sqrt{k_i^2+2bk_i+c} \in Z$ với vô số $k_i$ nguyên và $c=a^2+b^2>0$

Mặt khác $MA_i^2=(k_i+[b])^2+c+2\left \{ b\right \}-[b]^2$.

TH1: $c+2\left \{ b\right \}-[b]^2>0$ thì $(k_i+[b]+1)^2>MA_i^2>(k_i+[b])^2$ với $k_i$ nguyên đủ lớn.

TH2: $c+2\left \{ b\right \}-[b]^2<0$ thì $(k_i+[b])^2>MA_i^2>(k_i+[b]-1)^2$ với $k_i$ nguyên đủ lớn.

Suy ra điều vô lí. (chú ý $c+2\left \{ b\right \}-[b]^2$ khác 0)

Vậy....

Cho $a=b=1$ ta có $u_1^2=u_1 \Rightarrow u_1 \in{0;1}$.Mặt khác $u_n$ tăng thực sự trên $R$ nên $u_1=1$.
Với mỗi $a \in Z^+$ đặt :
$M= \left \{\frac{u_{x+a}}{u_x}:x\in N^*;(x,a)=1\right \}$
$N= \left \{\frac{u_{x}}{u_{x+a}}:x\in N^*;(x,a)=1\right \}$
Do $u_n$ tăng thực sự nên tồn tại $A=infM$ và $B=supN$ với $B\leq1 \leq A$.
Ta có: Với mỗi số nguyên dương $m$, gọi $x_0$ là số nguyên tố $>ma$. Khi đó $(x_0,2)=(x_0,ka)=1,\forall k\in N^*,k\leq m$
Ta có:
$u_2.u_{x_0}=u_{2x_0}\geq u_{x_0+ma} \geq A.u_{x_0+(m-1)a}\geq...\geq A^m.u_{x_0}$
$\Rightarrow u_2\geq A^m \Rightarrow A=1$
$u_{x_0}\leq B.u_{x_0+a} \leq B^2.u_{x_0+2a} \leq ... \leq B^m.u_{2x_0}=B^m.u_{x_0}.u_2$
$\Rightarrow u_2.B^m=1 \Rightarrow u_2=1$
Suy ra $A=B=1$.
Tiếp tục ta sẽ chứng minh dãy $u_n$ có tính nhân tính.Thật vậy,xét $(x,a)=1$ ta có:
$u_{x+a}.u_a=u_{ax+a^2} \geq u_{ax+1}= \frac{u_{ax+1}.u_{a^k}}{u_{a^k}}= \frac{u_{a^{k+1}x+a^k}}{a^k} \geq \frac{u_{a^{k+1}x}}{u_{a^k}}= \frac{u_x.u_{a^{k+1}}}{u_k}$
Suy ra: $\frac{u_{x+a}}{u_x} \geq \frac{u_{a^{k+1}}}{u_{a^k}.u_a}$
Tương tự ta có:
$u_x.u_a \leq \frac{u_{ax}.u_{a^k}}{u_{a^k}} \leq \frac{u_{x+a}.u_{a^{k+1}}}{u_{a^k}}$
$\Rightarrow \frac{u_{x}}{u_{x+a}} \leq \frac{u_{a^{k+1}}}{u_{a^k}.u_a}$
Suy ra: $A \leq \frac{u_{a^{k+1}}}{u_{a^k}.u_a} \geq B$
Hay $\frac{u_{a^{k+1}}}{u_{a^k}.u_a}=1 \Rightarrow u_{a^{k+1}}=u_{a}.u_{a^k}$.
Kết hợp với giả thiết suy ra $u_{xy}=u_x.u_y, \forall x,y\in N$
Chứng minh tính duy nhất của dãy.
Giả sử tồn tại $u_2=c$ và có hai dãy thõa mãn bài toán là $u_n$ và $v_n$ với $u_2=v_2=1$ và tồn tại $t>2$ sao cho $u_t \neq v_t$.
Với mỗi $s\in N^*$ thì tồn tại duy nhất $k$ sao cho $2^k\leq t^s<2^{k+1}$.
Suy ra $u_{2^k} \leq u_{t^s}<u_{2^{k+1}}$ hay $k.lnc \leq sln(u_t) <(k+1)lnc$. Tương tự đối với $v_n$, ta có:
$\frac{k}{k+1} \leq \frac{u_t}{v_t} <\frac{k+1}{k}$.
Cho $k$ tiến tới vô cùng suy ra $u_t=v_t$, vô lí.
Do đó $u_n$ là duy nhất.
Dễ thấy dãy $u_n=n^{\alpha}$ với $\alpha>0$ là dãy số thõa mãn.
Vậy ....

Đề của Gogo123:

Tìm tất cả các dãy số $(u_n)_{n\geq 1}^{\infty }$ tăng thực sự thõa mãn:

$$u_{m.n}=u_m.u_n$$

với mọi $m,n$ nguyên tố cùng nhau.

 

Lời giải gogo123 xin gửi sau vì bây giờ em phải đi học Trường xuân nên không đủ thời gian viết.Mong BTC thông cảm.

(Chú ý bài trên tuyệt đối không phải là bài toán Số học mà lời giải của nó là Dãy số giới hạn)

Đúng là mình sai ở đó.Lúc đổi hàm mình đổi nhầm nên lúc cuối ra kết quả phải làm mất con 1 đi.

Sup là cận trên , Inf cận dưới

Bài 1: Cho hàm số $f\left ( x \right )$ liên tục trên đoạn [a;b]. Chứng minh rằng với mọi $x_{1},x_{2}$ thuộc đoạn $[a;b]$ đều tồn tại ít nhất một điểm c thuộc đoạn $[x_{1};x_{2}]$ sao cho $f©=\frac{1}{2}[f(x_{1})+f(x_{2})]$

Đặt $Sup_{x\in[x_1;x_2]}=f(x_0);Inf_{x\in[x_1;x_2]}=f(x'_0)$
Xét hàm số $g(x)=f(x)-\frac{1}{2}(f(x_1)+f(x_2))$, ta có $g(x_0).g(x'_0)<0$ suy ra tồn tại nghiệm $x=c$ của phương trình $g(x)=0$ thuộc $(x_0,x'_0)$, hay $c\in[x_1,x_2]$.
Ta có đpcm

Trước hết ta sẽ giải bài toán sau:
Bài toán 1:Tìm hàm số $g(x):N\rightarrow R$ thoã mãn : $g(2x+y)-g(2x)-g(y)=g(2y+x)-g(2y)-g(x)$
Lời giải: Trước hết ta cần chú ý một tính chất sau (rất hay).
Tính chất: Nếu ta gọi S là một không gian vector k-thành phần, khi đó nếu một tập hợp vector A được xác định khi k giá trị tương ứng với k thành phần của S thì các vector trong A có thể biểu diễn tổng quát bằng k thành phần trong S.
(Tc này có thể tưởng tượng như trong không gian 2 hoặc 3 chiều, nếu một dãy số (dãy vector) $u_n$ xác định khi biết k giá trị $u_1,...,u_k$ thì tồn tại công thức truy hồi tính $u_{n+k+1}$ thông qua $u_n;u_{n+1};...;u_{n+k}$)
Trở lại Bài toán 1:
Thế $y=1$ ta có: $g(2x+1)=g(2x)+g(1)+g(x+2)-g(2)-g(x)$
$y=2$ ta có: $g(2x+2)=g(2x)+g(2)+g(x+4)-g(4)-g(x)$
Như vậy,vì hàm số $g$ có đối số $x$ chạy trên $N$ nên $g(x)$ được xác định khi biết các giá trị $g(1);g(2);g(3);g(4);g(6)$, áp dụng tính chất ở trên bây giờ ta sẽ tìm 5 nghiệm của $g(x)$ phân biệt (không bị suy ra từ nghiệm khác) làm hệ vector cơ sở để biểu diễn tập vector nghiệm của $g(x)$.
Ta có thể thấy các nghiệm sau:
$g_1(x)=1;g_2(x)=x;g_3(x)=x^2$
$g_4(x)=1$ khi $x\equiv 0(mod2)$ và $g_4(x)=0$ khi $x\equiv 1(mod2)$
$g_5(x)=1$ khi $x$ chia hết cho 3, $g_5(x)=0$ khi $x$ không chia hết cho 3.
Vậy ta có thể biểu diễn tất cả các nghiệm của $g(x)$ là :
$g(x)=a.x^2+b.x+c+d.g_4(x)+e.g_5(x)$ (1)

Trở lại bài toán ban đầu đề bài:
Đổi hàm $f$ bởi hàm $f-1$ thì bài toán trở thành tìm hàm $f$ liên tục trên $R$ thoã mãn
$$f(x+y)+f(xy)+1=f(x)+f(y)+f(xy+1)$$
Trước hêt ta sẽ tìm hàm trên $Q$
Dễ thấy $f(1)=1$,thế $(x,y)\rightarrow (xy,z)$ và $(x,y)\rightarrow (xz,y)$ ta suy ra được phương trình hàm $f$ với 3 biến: $f(xy+z)-f(xy)-f(z)=f(xz+y)-f(xz)-f(y)$ (2)
Thế ở (2) $(x,y,z)\rightarrow (2,\frac{m}{p},\frac{n}{p})$ với $m,n,p$ nguyên dương, ta được
$$f(\frac{2m+n}{p})-f(\frac{2m}{p})-f(\frac{n}{p})=f(\frac{2n+m}{p})-f(\frac{2n}{p})-f(\frac{m}{p})$$
Suy ra $f(\frac{x}{p})$ (x nguyên dương) có tập nghiêm như ở (1) hay $f(\frac{x}{p})=a_p.x^2+b_p.x+c_p+d_p.g_4(x)+e_p.g_5(x)$
Thế $x=kp$ ta được $a_p=\frac{a}{p^2} \Rightarrow b_p=\frac{b}{p}$
Tiếp tục thế $x=2kp;x=3kp;x=6kp$ ta có $c_p=c;d_p=e_p=0$
Hay $f(x)=ax^2+bx+c$ với mọi số hữu tỉ dương $x$.
Mà $f$ liên tục trên $R$ và $Q^+$ trù mật trong $R^+$ nên $f(x)=ax^2+bx+c$ vói mọi $x>0$.

Tiếp tục xử lí bài toán cho TH $x<0$ ta thế $(x,y,z)\rightarrow (2,-\frac{m}{p};-\frac{n}{p})$ ta được
$f(-\frac{2m+n}{p})-f(-\frac{2m}{p})-f(-\frac{n}{p})=f(-\frac{2n+m}{p})-f(-\frac{2n}{p})-f(-\frac{m}{p})$
Suy ra $f(-\frac{x}{p})$ lấy (1) làm tập nghiệm, tiếp tục xử lí như TH $x>0$ ta cũng được kết quả tương tự là $f(x)=a'x^2+b'x+c'$ với mọi $x<0$.

Như vậy $f(x)=ax^2+bx+c$ vói mọi $x>0$ và $f(x)=a'x^2+b'x+c'$ với mọi $x<0$.
Cho $x$ tiến đến $0^+$ và $0^-$ trong 2 TH ta được $c=c'$.
$f(1)=1 \Rightarrow c=1-a-b$
Thế $(x,y)=(-1,-1) \Rightarrow a'=a$
$(x,y)=(-2,3) \Rightarrow b'=b$
Hay $f(x)=ax^2+bx-a-b+1$ với mọi số thực $x$.
Thử lại dễ thấy hàm số này thoã mãn bài toán.

Vậy $f(x)=ax^2+bx+2-a-b$ là hàm số cần tìm.

 

Bài làm chưa chính xác, sai lầm đã được Joker999 chỉ ra ở dưới.

Điểm bài: 7

S = 13 + 7*3 = 34