.

. 

Xem xong bài viết này em quyết định chi 10 tỷ vì chức vụ ĐHV Tổng hợp

$\boxed{\text{Problem 2}}$ (Balkan MO 2015)

Chứng minh rằng trong $20$ số nguyên dương liên tiếp có một số nguyên dương $d$ sao cho với mọi số nguyên dương $n$, bất đẳng thức sau đúng:

$n\sqrt{d}\left \{ n\sqrt{d} \right \}>\frac{5}{2}$

Cho $k$ là số nguyên dương chẵn. $N$ là tích của $k$ số nguyên tố phân biệt $p_1,...,p_k$.  $a,b$ là hai số nguyên dương phân biệt sao cho $a \leq b \leq N$. Gọi $S_1$ và $S_2$ là hai tập thỏa mãn:$ S_1=\{d| $ $ d|N, a\leq d\leq b, d $ có số ước nguyên tố chẵn $\}$, $ S_2=\{d| $ $ d|N, a\leq d\leq b, d $ có số ước nguyên tố lẻ $\}$. Chứng minh rằng: $\left | S_1 \right |-\left | S_2 \right |\leq C_{k}^{\frac{k}{2}}$

Theo em được biết thì VMF mình có 2 Hiệp sĩ là Cao Xuân Huy và nguyenta98 đạt giải nhì

P/s: em cũng vậy (khoe khoang tí )

$n$ là nguyên dương và $|S|=2^n+1$.Cho $f$ là hàm từ tập các tập con hai phần tử của $S$ tới $\{0,1,...,2^{n-1}-1\}$ sao cho với mỗi $f(\{x,y\}),f(\{y,z\}),f(\{z,x\})$ sẽ bằng tổng hai số còn lại.Chứng minh có tồn tại $f(\{a,b\})=f(\{b,c\})=f(\{c,a\})=0$.

Ta chứng minh bằng quy nạp.

Với $n=1$ thì bài toán hiển nhiên đúng.

GIả sử bài toán đúng với $n=k$, $k \geq 1$

Xét $n=k+1$:

Xét $a \in S$, ta quy ước $f\left ( \left \{ a,a \right \} \right )=0$

Ta phân hoạch $S$ thành $2$ tập $U,V$ như sau:

Với $x \in S$, $x \in U$ kvck $f\left ( \left \{ x,a \right \} \right )$ chẵn

Với $x \in S$, $x \in V$ kvck $f\left ( \left \{ x,a \right \} \right )$ lẻ

Theo nguyên tắc Dirichlet, tồn tại một trong $2$ tập $U,V$ có số phần tử không nhỏ hơn $2^k+1$

Giả sử $\left | U \right | \geq 2^k+1$

Với mọi x,y thuộc $U$, ta có $f\left ( \left \{ x,a \right \} \right )+f\left ( \left \{ y,a \right \} \right )+f\left ( \left \{ x,y \right \} \right ) \vdots 2$

$f\left ( \left \{ x,a \right \} \right )+f\left ( \left \{ y,a \right \} \right ) \vdots 2$

Suy ra $f\left ( \left \{ x,y \right \} \right ) \vdots 2, \forall x,y \in U$

Đặt $g\left ( \left \{ x,y \right \} \right )=\frac{f\left ( \left \{ x,y \right \} \right )}{2}$ $\Rightarrow g\left ( \left \{ x,y \right \} \right ) \in \left \{ 0,...,2^{k-1}-1 \right \}$

Theo giả thiết quy nạp, tồn tại $x,y,z \in U$ sao cho $g\left ( \left \{ x,y \right \} \right )=g\left ( \left \{ x,z \right \} \right )=g\left ( \left \{ y,z \right \} \right )=0$

Suy ra  $f\left ( \left \{ x,y \right \} \right )=f\left ( \left \{ x,z \right \} \right )=f\left ( \left \{ y,z \right \} \right )=0$

Theo nguyên lí quy nạp, ta có đpcm

Bài 40 : Tìm hàm $f$ liên tục $\mathbb{R}\to \mathbb{R}$ sao cho $f(x)-f(y)\in \mathbb{Q}\forall x-y \in \mathbb{Q}$

Đặt $g(x)=f(x)-f(0)$, ta có $g(0)=0$ và $g(x)-g(y) \in \mathbb{Q}\Leftrightarrow x-y \in \mathbb{Q}$

Cố định số hữu tỉ $r$, xét $h(x)=g(x+r)-g(x)$

Ta có $h(x) \in \mathbb{Q}, \forall x \in\mathbb{R}$

Mà $h$ liên tục trên $\mathbb{R}$ nên $h(x)=const$

$h\left ( 0 \right )=g\left ( r \right )\Rightarrow g\left ( x+r \right )=g\left ( x \right )+g\left ( r \right ), \forall r \in \mathbb{Q}$

Từ đây, ta chứng minh được $g\left ( x \right )=xg(1), \forall x \in \mathbb{Q}$

Mà $g$ liên tục trên $\mathbb{R}$ nên $g\left ( x \right )=xg\left ( 1 \right ),\forall x \in \mathbb{R}$

Suy ra $f\left ( x \right )\equiv ax+b$ với $a,b \in \mathbb{Q}$ (thử lại thấy thỏa mãn)

Bài 46: Cho tập $S$ gồm $1953$ điểm thỏa mãn $2$ điểm bất kì của $S$ cách nhau ít nhất $1$ cm. Chứng minh rằng: tồn tại tập con của $S$ có $217$ điểm sao cho $2$ điểm bất kì trong tập con đều có khoảng cách ít nhất $\sqrt{3}$ cm.

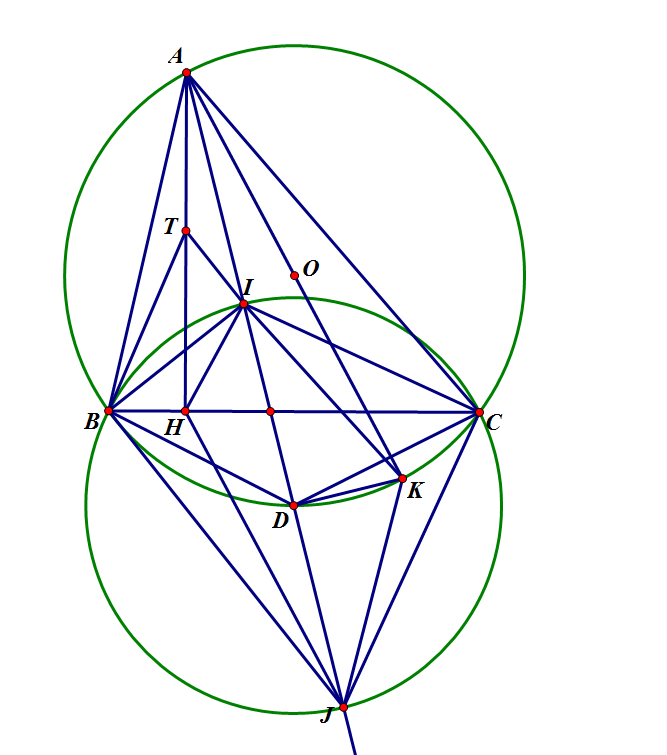
Bài 41 : Cho tam giác $ABC$ nội tiếp đường tròn $(O)$. $H$ là hình chiếu của $A$ xuống $BC$, $AK$ là đường kính của $(O)$. $I$ và $J$ lần lượt là tâm đường tròn nội tiếp và bàng tiếp góc $A$ của $\Delta \,ABC$. Chứng minh rằng $\widehat{BIH}=\widehat{CIK}$ và $\widehat{BJH}=\widehat{CJK}$

Giả sử $AC > AB$

Gọi $D$ là giao điểm $AI$ và đường tròn tâm $O$

Ta cần chứng minh $\angle BIH=\angle CIK\Leftrightarrow \angle DIB-\angle DIC=\angle HID-\angle KID$

$\angle IBC-\angle ICB=\angle HID-\angle KID$

Gọi $T$ sao cho $TI \perp BI$ với $T \in AH$

Ta có: $\angle IBC=\angle HTI=\angle HAI+\angle TIA=\angle HAI+\angle ICB$

Vậy đpcm tương đương với:

$\angle HID=\angle HAI+\angle DIK$

$\Leftrightarrow \angle AHI=\angle DIK$ (1)

Ta có $I,B,C,J$ nằm trên đường tròn tâm $D$, $D$ là trung điểm của $IJ$

Mặt khác, $\angle ADK= 90^0$

Suy ra tam giác $IKJ$ cân tại $K$

Suy ra $\angle KID = \angle KJD$ (2)

$\angle HAI = \angle JAK$, $\frac{AH}{AI}=\frac{AJ}{AK}$ nên tam giác $AHI$ đồng dạng với tam giác $AJK$

Suy ra $ \angle AHI=\angle AJK$ (3)

Từ (1), (2), (3), ta có đpcm

Để chứng minh $\angle BJH=\angle CJK$, ta cần chứng minh:

$\angle JHI= \angle JKI$

$\Leftrightarrow IHC=\angle DKJ\Leftrightarrow \angle AHI=\angle DIK$ @~> đpcm

Bài 37: Cho các số nguyên $x,y,z$ với $x>2,y>1,z>0$ thỏa mãn:

$x^y+1=z^2$

Gọi $p$ là số ước nguyên tố phân biệt của $x$, $q$ là số ước nguyên tố phân biệt của $y$. Chứng minh rằng: $p \geq q+2$

Bài 35: Cho $2$ tập hợp $T$ và $P$, $T$ chứa $66$ điểm, $P$ chứa $16$ đường thẳng. $(A,l)$ được gọi là tốt nếu $A \in T$, $l \in P$, $A \in l$. Tìm số bộ tốt lớn nhất.

 

Bài 2: Tô tập số nguyên bởi $4$ màu. $x,y$ là số nguyên lẻ thỏa mãn $\left | x \right |$ khác $\left | y \right |$ . CMR: tồn tại 2 số nguyên cùng màu có hiệu thuộc ${x,y,x+y,x-y}$.

 

Giả sử phản chứng: tồn tại một cách tô tập $Z$, $f: \mathbb{Z}\rightarrow \left \{ X,D,T,V \right \}$ sao cho với mọi $a \in Z$, ta có:

$\left \{ f\left ( a \right ),f\left ( a+x \right ),f\left ( a+y \right ),f\left ( a+x+y \right ) \right \}=\left \{ X,D,T,V \right \}$

Xét $g:\mathbb{Z}^2\rightarrow \left \{ X,D,T,V \right \}$ sao cho $g\left ( i,j \right )=f\left ( ix+jy \right )$

Biểu diễn các điểm này trên mạng lưới nguyên

4 đỉnh của một hình vuông đơn vị đôi một khác màu

Xét một cột bất kì

Nếu tồn tại $3$ đỉnh liên tiếp trên cột khác màu thì cách tô trên t/m:

+)Mỗi hàng chỉ có $2$ màu

+)Nếu $2$ hàng cách nhau một số chẵn thứ tự thì cùng tập màu (*)

Nếu một cột bất kì không tồn tại $3$ ô liên tiếp khác màu khì (*) sẽ đúng cho các cột. Không mất tính tổng quát, giả sử (*) đúng.

Giả sử hàng $y=0$ được tô màu D,V

Nếu $g\left ( 0,0 \right )=D\Rightarrow g\left ( 0,y \right )=V,g\left ( x,0 \right )=V$

$\Rightarrow g\left ( 0,x \right )=f\left ( xy \right )=g\left ( y,0 \right )=V$

Mặt khác,  hàng chứa $\left ( 0,x \right )$ là hàng thứ $x$, hàng chứ $\left ( y,0 \right )$ là hàng thứ 0, suy ra vô lí

Vậy ta có đpcm

Hưởng ứng vài bài lí thuyết đồ thị

Bài 12: Cho một ngôi trường có $n$ khóa học và $n$ học sinh. Các học sinh đăng kí vào lớp học, không có $2$ học sinh nào tham gia các khóa học hoàn toàn giống nhau. CMR: ta có thể đóng cửa một khoá học sao cho vẫn không có hai học sinh nào tham gia các khoá học hoàn toàn going nhau.

Bài 13: Cho $35$ người đi dự một buổi họp. Có tất cả $112$ căp hai người quen nhau. Chứng minh rằng tồn tại $4$ người $a,b,c,d$ sao cho $a$ quen $b$, $b$ quen $c$, $c$ quen $d$ và $d$ quen $a$.

Topic đóng bụi quá dày rồi ! 

Làm một bài để '' quét dọn '' 

Bài 47 : ( pp truy hồi )  Tìm số hoán vị của tập $A={1,2,...,n}$ sao cho mỗi hoán vị đều thỏa : $2.(a_{1}+a_{2}+...+a_{n})\vdots k$ ( với $k\in {1,2,...,n}$ ) 

Lâu rồi mới có người quét dọn

Bài này là IMOSL 2008

http://www.artofprob...4446f0#p1472110

   SỞ GIÁO DỤC VÀ ĐÀO TẠO                                             KỲ THI CHỌN HSG TỈNH LỚP 12 THPT

                 BÌNH ĐỊNH                                                                       KHÓA NGÀY:22-10-2014

            ĐỀ CHÍNH THỨC                                Môn thi:               Toán

                                                                          Thời gian:             180 phút

                                                                          Ngày thi:              22/10/2014

                                                                          -----------------------------------------------

Bài 1: (4 điểm )

Giải hệ phương trình:

$\left\{\begin{matrix} 2x+\frac{1}{x+y}=3\\ 4xy+4x^2+4y^2+\frac{3}{\left ( x+y \right )^2}=7 \end{matrix}\right.$

Bài 2: (4 điểm)

a)      Cho p là một số nguyên tố, k là một số nguyên dương. Một đường trong được chia thành p cung bằng nhau. Tiến hành tô các cung bằng k màu khác nhau ( mỗi cung được tô bằng một màu). Hai cách tô màu được coi là giống nhau nếu cách tô này sẽ thu được từ cách tô kia qua một phép quay với tâm là tâm của đường tròn. Hỏi có bao nhiêu cách tô màu khác nhau? (Cách chứng minh định lí Fermat nhỏ bằng tổ hợp)

b)      Tìm tất cả các đa thức  thỏa mãn điều kiện: $P\left( x \right)=\sqrt{P\left( {{x}^{2}}+1 \right)-7}+6,\forall x\ge 0,P\left( 0 \right)=6$

Bài 3: (4 điểm)

Cho số thực . Xét dãy số  xác định bởi:

$\left\{\begin{matrix} x_1=a\\ x_{n+1}=1+ln\left ( \frac{x_n^2}{1+lnx_n} \right ) \end{matrix}\right.$ với n=1,2,…

Chứng minh rằng dãy số có giới hạn hữu hạn và tìm giới hạn đó.

Bài 4: (4 điểm)

Cho tam giác ABC nội tiếp đường tròn (O;R). Với mỗi điểm M trong đường tròn ta gọi A’,B’,C’ lần lượt là giao điểm của AM,BM,CM với đường tròn. Tìm tập hợp các điểm M trong đường tròn thỏa mãn hệ thức sau:

$\frac{MA}{MA'}+\frac{MB}{MB'}+\frac{MC}{MC'}\le 3$

Bài 5: (4 điểm)

Cho 2 điểm cố định $A, B$ và điểm  di động trên mặt phẳng sao cho $\hat{ACB}=a \ (0<a<180)$ không đổi cho trước. Hình chiếu của tâm đường tròn nội tiếp $I$ của tam giác $ABC$ xuống ba cạnh $AB,\ BC,\ CA$ lần lượt là $D,E,F$. $AI$ và $BI$ cắt $EF$ lần lượt tại $M,N$.
a) Chứng minh độ dài $MN$ không đổi.
b) CM đường tròn $(DMN)$ luôn đi qua một điểm cố định.

Câu 4 :

Với mỗi số nguyên dương $n$, đặt $S_{n}=\{1;2;...;n\}$. Phần tử $j$ của $S_n$ được gọi là điểm bất động của song ánh $p \, : \, S_n\to S_n $ nếu $p(j)=j$. Gọi $f(n)$ là số song ánh từ $S_{n}$ đến $S_{n}$ mà không có điểm bất động nào, $g(n)$ là số song ánh từ $S_{n}$ đến $S_{n}$ mà có đúng 1 điểm bất động. Chứng minh rằng : $$|f(n)-g(n)|=1\,\,\,\forall n\in\mathbb{N}^{*}$$

Theo nguyên lí bao hàm-loại trừ, ta có:

$$f\left ( n \right )=n!\left ( 1-\frac{1}{1!}+\frac{1}{2!}-...+\frac{\left ( -1 \right )^{n}}{n!} \right )$$

$g\left ( n \right )=nf\left ( n-1 \right )=n!\left ( 1-\frac{1}{1!}+\frac{1}{2!}-...+\frac{\left ( -1 \right )^{n-1}}{(n-1)!} \right )$

Vậy $\left | f\left ( n \right )-g\left ( n \right ) \right |=1$

Tìm $m$ để hệ phương trình có $3$ nghiệm phân biệt:

$\left\{\begin{matrix} x+y=m\\ \left ( y+1 \right )x^2+xy=m\left ( x+1 \right ) \end{matrix}\right.$

Câu 3 (5 điểm)

Cho $n \geq 3$ là một số nguyên dương. Chứng minh với $n$ điểm phân biệt nằm trong mặt phẳng, sao cho trong đó không có 3 điểm nào thẳng hàng thì số tam giác có đỉnh được lấy trong $n$ điểm đã cho và có diện tích bằng $1$ không lớn hơn $\dfrac{2}{3}(n^2-n)$.

Ta giải bài sau bằng đếm 2 cách

Xét $2$ điểm bất kì. Vì không có $3$ điểm nào thẳng hàng nên tồn tại nhiều nhất $4$ tam giác có diện tích bằng 1 nhận $2$ điểm được chọn làm đỉnh.

Vậy có nhiều nhất $\frac{4}{3}C_{n}^{2}=\frac{2}{3}\left ( n^2-n \right )$ tam giác có diện tích bằng $1$

=================

P/s: ước gì số với tổ cũng lên ngôi tại tỉnh t :'(

 

Bài 2. Ta định nghĩa một domino là một cặp số nguyên dương khác nhau có sắp xếp (Ví dụ, ta có $(3,5)$ và $(5,3)$ là $2$ domino khác nhau). Một dãy domino được gọi là hoàn chình nếu gồm các domino khác nhau được sắp xếp sao cho số đầu của domino này sẽ bằng với số sau của domino liền trước; và $2$ domino $(i,j)$ và $(j,i)$ không được cùng xuất hiện trong dãy với mọi $i$ và $j$. Cho $D_n$ là tập hợp các domino với các số trong cặp không lớn hơn $n$. Hãy tìm chiều dài xa nhất mà một dãy domino hoàn chỉnh có thể đạt được khi được dựng từ các domino của $D_n$.

Xét đồ thị có $n$ đỉnh

Nhận xét: Chiều dài xa nhất mà một dãy domino hoàn chỉnh bằng số cạnh lớn nhất của đồ thị $n$ đỉnh chứa đường đi Euler.

Xét $2$ trường hợp:

TH1: $n=2k+1$

Xét đồ thị đầy đủ $n$ đỉnh. Bậc của mỗi đỉnh là số chẵn nên tồn tại một đường đi Euler. Vậy độ dài lớn nhất của dãy Domino hoàn chỉnh là $C_{n}^{2}$

TH2: $n=2k$

Khi đó, đồ thị đầy đủ $n$ đỉnh có các đỉnh bậc đều lẻ nên ta phải bỏ ít nhất $k-1$ cạnh để chỉ còn lại $2$ đỉnh bậc lẻ. Vậy độ dài lớn nhất của dãy Domino hoàn chỉnh là $C_{n}^{2}-\frac{n}{2}+1$

$\boxed{\text{Bài 6 (7đ)}}$

Với mỗi số nguyên dương n, gọi $f(n)$ là số cách thay các dấu $"\pm "$ trong biểu thức $\pm 1\pm 2\pm 3...\pm n$ bởi các dấu $"+"$ hoặc $"-"$ sao cho tổng đại số nhận được bằng 0. Chứng minh rằng:

a) $f(n)=0$ khi $n\equiv 1 (mod 4)$ hoặc $n\equiv 2 (mod 4)$

b)$2^{\frac{n}{2}-1}\leq f(n)<2^n-2^{\left [ \frac{n}{2} \right ]+1}$ khi $n\equiv 0 (mod 4)$ hoặc $n\equiv 3 (mod 4)$

 

a) Nhận xét: Khi thay dấu cộng thành trừ (và ngược lại), tính chẵn lẻ của tổng không đổi.

Với $n\equiv 1;2\left ( mod 4 \right )$ thì tổng $1+2+...+n$ lẻ

Vì vậy, $f\left ( n \right )=0$ khi $n\equiv 1;2\left ( mod 4 \right )$

b) Chứng minh $f\left ( n \right )\geq 2^{\frac{n}{2}-1}$

Với $n=3$ và $n=4$, mệnh đề trên hiển nhiên đúng.

Ta chứng minh rằng nến $n$ đúng thì $n+4$ cũng đúng

Xét dấu của các số $n+1;n+2;n+3;n+4$:

Nếu ta đặt các dấu là $\left ( n+1 \right )-\left ( n+2 \right )-\left ( n+3 \right )+\left ( n+4 \right )$ hoặc $-\left ( n+1 \right )+\left ( n+2 \right )+\left ( n+3 \right )-\left ( n+4 \right )$ và các dấu còn lại đặt như các bộ $f\left ( n \right )$ thì ta có bộ mới thỏa yêu cầu đề bài.

Đối với các bộ thuộc $f\left ( n \right )$ có $-1$ thì ta đổi thành$+1$ rồi thêm $\left ( n+1 \right )-\left ( n+2 \right )+\left ( n+3 \right )-\left ( n+4 \right )$ thì có được bộ mới

Đối với các bộ thuộc $f\left ( n \right )$ có $+1$ thì ta đổi thành$-1$ rồi thêm $-\left ( n+1 \right )+\left ( n+2 \right )-\left ( n+3 \right )+\left ( n+4 \right )$ thì có được bộ mới

Đối với các bộ thuộc $f\left ( n \right )$ có $-2$ thì ta đổi thành$+2$ rồi thêm $\left ( n+1 \right )+\left ( n+2 \right )-\left ( n+3 \right )-\left ( n+4 \right )$ thì có được bộ mới

Đối với các bộ thuộc $f\left ( n \right )$ có $+2$ thì ta đổi thành$-2$ rồi thêm $-\left ( n+1 \right )-\left ( n+2 \right )+\left ( n+3 \right )+\left ( n+4 \right )$ thì có được bộ mới

Vậy $f\left ( n+4 \right )\geq 4f\left ( n \right )\geq 2^{\frac{n+4}{2}-1}$

Suy ra đpcm

Chứng minh $f\left ( n \right )<2^n-2^{\left [ \frac{n}{2} \right ]+1}$

Gọi $g\left ( n \right )$ là số các bộ dấu sao cho tổng trên khác $0$

Ta cần chứng minh $g\left ( n \right )> 2^{\left [ \frac{n}{2} \right ]+1}$

Chứng minh bằng qui nạp

Với $n=3$ và $n=4$ thì ta có mệnh đề trên đúng.

Ta chứng minh với $n$ đúng thì $n+4$ cũng đúng.

Xét dấu của các số $n+1;n+2;n+3;n+4$

Đối với các bộ thuộc $f\left ( n \right )$, ta đặt dấu các số $n+1;n+2;n+3;n+4$ để tổng đại số chúng khác $0$. Có $14$  cách đặt dấu cho mỗi bộ như vậy.

Đối với các bộ thuộc $g\left ( n \right )$, ta đặt dấu các số $n+1;n+2;n+3;n+4$ để tổng đại số chúng bằng $0$. Có $2$ cách đặt như vậy cho mỗi bộ

Suy ra $g\left ( n+4 \right )\geq 14f\left ( n \right )+2g\left ( n \right )>14.2^{\frac{n}{2}-1}+2.2^{\left [ \frac{n}{2} \right ]+1}>2^{\left [ \frac{n+4}{2} \right ]+1}$

Vậy ta có đpcm

$\boxed{\text{Bài 7 (6đ)}}$

 

Các ô vuông của một bảng vuông kích thước $10x10$ được tô bởi các màu trắng hoặc đen sao cho trên mỗi hàng cũng như trên mỗi cột đều có đúng 3 ô được tô màu đen. Chẳng hạn như hình vẽ :

                                                                                

Chứng minh rằng trong mọi cách tô như vậy ta luôn có thể tìm ra 10 ô được tô màu đen sao cho không có hai ô nào nằm trên cùng một hàng hay trên cùng một hàng cột.

=======Hết=======

 

Ta xét đồ thị lưỡng phân $G=\left ( A,B,E \right )$, trong đó $A$ là tập hợp các đỉnh biểu thị các hàng, $B$ là tập hợp các đỉnh biểu thị các cột. Hai đỉnh được nối với nhau khi và chỉ khi hàng và cột tương ứng giao nhau tại một ô được tô màu.

Gọi $S\subset A$ là tập con các đỉnh thuộc $A$ và $N\left ( S \right )$ là tập hợp các đỉnh thuộc $B$ mà kề với một trong các đỉnh thuộc $S$

Số các ô đen của các hàng có đỉnh thuộc $S$ là $3\left | S \right |$

Vì mỗi cột chứa $3$ ô đen nên $\left | N\left ( S \right ) \right |\geq \left | S \right |$

Theo tiêu chuẩn Hall thì tồn tại một ghép cặp hoàn hảo từ $A$ đến $B$, suy ra đpcm.

Đầu tiên mình chân thành xin lỗi bạn Huong TH Phan

Mình nhận được báo cáo của bạn buiminhhieu về việc topic đó bị đặt sai box và đã nhắc nhở mà không xem bài viết đó ở trong box nào

Sau đó mình nhận thấy bài này hoàn toàn đúng box nên đã mở topic trở lại

Còn chuyện gỡ điểm nhắc nhở thì mình đã nhờ admin Ispectorgadget và mình nghĩ bạn sẽ sớm trở lại diễn đàn được thôi ( có thể trong vài giờ tới )

Chân thành xin lỗi

Cho $n$ là số nguyên dương bất kì. Chứng minh rằng:

$\left | \left \{ \left ( x,y \right )  \in \mathbb{Z}^2 \mid x^2+y^2=n \right \} \right |=4\left ( d_1\left ( n \right )-d_3\left ( n \right ) \right )$

($d_i\left ( n \right )$ là số các ước dương của $n$ đồng dư với $i$ mod $4$ )