Gọi $\mathbb{F}_{q}$ là một trường hữu hạn có $q$ phần tử. Xét $A, B\in M_{n}\left ( \mathbb{F}_{q} \right )$ hỏi bao nhiêu cặp $\left ( A, B \right )$ để $\operatorname{rank}A= \operatorname{rank}B= \frac{n}{2}$ và hệ $AX= B$ có nghiệm với $X\in M_{n}\left ( \mathbb{F}_{q} \right )$ là ẩn.

Gọi $\mathbb{F}_{q}$ là trường hữu hạn có $q$ phần tử với $q= p^{r}$ với $p$ nguyên tố và $r$ là số tự nhiên. Tìm số ma trận $A\in M_{n}\left ( \mathbb{F}_{q} \right )$ để $\operatorname{rank}A= m.$

Giả sử tất cả mỗi người có số nguyên quen là số lẻ.

Gọi số người quen của $45$ người lần lượt là $a_1,a_2,\dots,a_{45}$ trong đó $a_i$ là các số lẻ.

Khi đó tổng $a_1+a_2+\dots+a_{45}$ là số lẻ. Tuy nhiên, ở đây mỗi cặp quen nhau được tính hai lần (chẳng hạn người $i$ quen người $j$ thì lượt quen này được tính cho cả $a_i$ và $a_j$) nên tổng phải là số chẵn.

Do đó, phải tồn tại một người có số người quen là số chẵn.

Cách giải thực ra có thể đơn giản hơn, ta sẽ chứng minh số $\frac{-144}{1008}=\frac{-1}{7}$ luôn xuất hiện trên bảng. Từ đó suy ra số cuối cùng trên bảng là: $\frac{-1}{7}.$0

Thật vậy, trong mỗi bước của quy trình, nếu số $\frac{-1}{7}$ là một trong hai số được số thì số được thêm vào là:

$\frac{-1}{7}+7.\frac{-1}{7}.y+y=\frac{-1}{7}.$ 

Còn nếu trong mỗi bước của chu trình số $\frac{-1}{7}$ không tham gia thì hiển nhiện số $\frac{-1}{7}$ vẫn nằm ở trên bảng.

Từ đó ta có điều phải chứng minh!

Đây là một cách trong tài liệu mình viết hồi lớp 11

Mình xin giải quyết câu cuối:

 

Ta chia bài toán trên thành 2 bước:

Bước1 : 

Ta chứng minh với a cầu thủ thì luôn tìm được một cách xếp sao cho khoảng giữa hai cầu thủ xếp liền nhau là a

Thật vậy, ta nhận thấy với 3 cầu thủ thì có cách xếp sao cho 3 cầu thủ bằng điểm nhau

Xét b-1 cầu thủ có điểm số bằng nhau. Ta chứng minh với b cầu thủ thì cũng chia được. Tuy nhiên điều này hiển nhiên vì nếu cầu thủ được thêm vào hòa với b-1 cầu thủ còn lại thì số điểm của họ là bằng nhau

Giờ ta xét a-1 cầu thủ có điểm bằng nhau.

Ta nhận thấy sau mỗi trận đấu thì tổng điểm thu được của 2 cầu thủ là 2

=> Số điểm của mỗi a-1 cầu thủ là a-2

Lấy thêm một cầu thủ bất kì và cho nó thẳng a-1 đứa còn lại

=> Tổng điểm nó thu được 2.(a-1)

=> Khoảng cách giữa hai cầu thủ xếp liền nhau là a

Bước 2:

Theo bước 1, ta có với n cầu thủ thì sẽ tồn tại một khoảng cách là n

Ta chứng minh n này là lớn nhất

Thật vậy với n=3 => đpcm

Giả sử nó đúng với n-1 cầu thủ ( có nghĩa là khoảng cách lớn nhất là n-1)

Ta chứng minh nó cũng đúng với n cầu thủ.

Gọi thẳng được thêm vào n-1 cầu thủ kia là A.

Ta nhận thấy nếu A được xếp nằm giữa n - 1 cầu thủ kia thì hiển nhiên khoảng cách giữa A và thằng xếp liền kề sẽ nhỏ hơn n-1

Xét 2 trường hợp:

+,  A đứng trước thằng xếp thứ nhất

Ta nhận thấy tổng số điểm của n-1 thẳng ban đầu là ( n-1 )(n-2)

Tổng số điểm của n thằng sau là n(n-1)

=> Điểm của A sẽ bé hơn hoặc bằng :

                 n(n-1) - (n-1)(n-2) = 2n - 2

Mặt khác ta lại có thằng đứng nhì ( đứng sau A) sẽ có điểm lớn hơn hoặc bằng:

                (n-1)(n-2) : (n-1) = n-2

=> Khoảng cách điểm giữa A và thẳng vừa nói trên sẽ bé hơn hoặc bằng:

                2n - 2 - n + 2 = n ( thỏa mãn )

=> đpcm

+,  A đứng sau thằng sếp cuối

     Chứng minh tương tự như trên

Vậy đáp số bài toán là n

 

P/s : Các cầu thủ là các đội bóng

Cho tô đỏ có vấn đề nhé, và cấu hình thỏa mãn không phải là duy nhất.

Chẳng hạn mình đưa ra cấu hình thỏa mãn sau.

Các đội $A_1,A_2,...,A_n$, với mỗi $k$ bất kì ta xét cấu hình thắng thua hòa như sau:

$A_1,...,A_k$ đội một hòa nhau tương tự $A_{k+1},A_{k+2},...,A_n$ đôi một hòa nhau.

Và một đội bất kì trong nhóm $A_1,A_2,...,A_k$ đều thắng một đội bất kì trong $A_{k+1},A_{k+2},...,A_n.$ 

Khi đó thì số điểm của $A_1=A_2=...=A_k = k-1 + 2(n-k)$ và $A_{k+1}=A_{k+2}=...=n-k-1.$

Khi đó $A_k - A_{k+1} = 2(n-k)+k-1 - (n-k-1) = n.$

Bên cạnh chỉ ra cấu hình trên thì cũng là một cách đưa ra luôn lời giải. Theo hai bước như sau

giả sử số điểm sau khi kết thúc giải đấu là $A_1 \ge A_2 \ge ... \ge A_n.$

Khi đó ta chứng minh được với mọi $k=1,2,...,n$ thì $n- k \le A_k \le 2(n-k)+k-1.$ 

Từ đấy ta có $A_k-A_{k+1} \le n.$

Mình xin giải quyết câu cuối:

 

Ta chia bài toán trên thành 2 bước:

Bước1 : 

Ta chứng minh với a cầu thủ thì luôn tìm được một cách xếp sao cho khoảng giữa hai cầu thủ xếp liền nhau là a

Thật vậy, ta nhận thấy với 3 cầu thủ thì có cách xếp sao cho 3 cầu thủ bằng điểm nhau

Xét b-1 cầu thủ có điểm số bằng nhau. Ta chứng minh với b cầu thủ thì cũng chia được. Tuy nhiên điều này hiển nhiên vì nếu cầu thủ được thêm vào hòa với b-1 cầu thủ còn lại thì số điểm của họ là bằng nhau

Giờ ta xét a-1 cầu thủ có điểm bằng nhau.

Ta nhận thấy sau mỗi trận đấu thì tổng điểm thu được của 2 cầu thủ là 2

=> Số điểm của mỗi a-1 cầu thủ là a-2

Lấy thêm một cầu thủ bất kì và cho nó thẳng a-1 đứa còn lại

=> Tổng điểm nó thu được 2.(a-1)

=> Khoảng cách giữa hai cầu thủ xếp liền nhau là a

Bước 2:

Theo bước 1, ta có với n cầu thủ thì sẽ tồn tại một khoảng cách là n

Ta chứng minh n này là lớn nhất

Thật vậy với n=3 => đpcm

Giả sử nó đúng với n-1 cầu thủ ( có nghĩa là khoảng cách lớn nhất là n-1)

Ta chứng minh nó cũng đúng với n cầu thủ.

Gọi thẳng được thêm vào n-1 cầu thủ kia là A.

Ta nhận thấy nếu A được xếp nằm giữa n - 1 cầu thủ kia thì hiển nhiên khoảng cách giữa A và thằng xếp liền kề sẽ nhỏ hơn n-1

Xét 2 trường hợp:

+,  A đứng trước thằng xếp thứ nhất

Ta nhận thấy tổng số điểm của n-1 thẳng ban đầu là ( n-1 )(n-2)

Tổng số điểm của n thằng sau là n(n-1)

=> Điểm của A sẽ bé hơn hoặc bằng :

                 n(n-1) - (n-1)(n-2) = 2n - 2

Mặt khác ta lại có thằng đứng nhì ( đứng sau A) sẽ có điểm lớn hơn hoặc bằng:

                (n-1)(n-2) : (n-1) = n-2

=> Khoảng cách điểm giữa A và thẳng vừa nói trên sẽ bé hơn hoặc bằng:

                2n - 2 - n + 2 = n ( thỏa mãn )

=> đpcm

+,  A đứng sau thằng sếp cuối

     Chứng minh tương tự như trên

Vậy đáp số bài toán là n

 

P/s : Các cầu thủ là các đội bóng

Bước quy nạp của bạn có vấn đề vì khi thêm $A$  vào đồng nghĩa với việc số điểm của từng thành viên trong $n-1$ cần thủ sẽ phải thay đổi nên việc xếp $A$ ở giữa hàng vẫn chưa thể suy ra được khoảng cách nó bé hơn $n-1.$

Chào mọi người, hiện tại mình đang dự định viết một chuyên đề về nguyên lý cực hạn dành cho THCS - chủ yếu dành cho những người mới bắt đầu làm quen về tổ hợp nên mình xin phép lên đây, ai có tài liệu gì về nguyên lý cực hạn (Càng cơ bản càng tốt) thì có thể cho mình tham khảo được không?

Cảm ơn mọi người.

Cho mình xin tài liệu về tổ hợp và rời rạc dành cho học sinh THCS với, ai có gửi link cho mình hoặc tên sách nhé.

Mình cảm ơn!

Với $n$ là số nguyên dương cho trước. Đặt $P(x)=x^n+x^{n-1}+...+x+1$.

Chứng minh rằng đa thức $P'(x)=nx^{n-1}+(n-1)x^{n-2}+...+2x+1$ bất khả quy trên $\mathbb{Z}$.

Bài 61. Cho $ a,b \in \mathbb{R}, a<b $. Giả sử rằng hàm $f(x)$ dương trên $(a,b)$ thỏa mãn $f(a)=f(b)=0$ và $f$ khả vi cấp 2. Chứng minh rằng:

  $ \int_a^b |\dfrac{f''(x)}{f(x)}|dx \ge \dfrac{1}{b-a}$

Chào mọi người, mình post bài viết này mong mọi người ủng hộ để có thể sưu tập được các bài toán tổ hợp liên quan đến trò chơi, luật chơi hay thuật toán để dành chiến thắng.

Mong ban quản trị không khóa bài viết ạ.

Cảm ơn mọi người.

Ai có bài toán nào vui lòng trả lời ở dưới bài viết hộ mình luôn nhé!

Ta có theo định nghĩa của $f$ thì:

$ f(X+Y)=(X+Y)A=XA+YA=f(X)+f(Y) ; \forall X,Y \in M_2 $
Và hiển nhiên: $f(aX)=aXA=a.f(X)$

Từ đó ta có $f$ là ánh xạ tuyến tính

Với mọi số nguyên dương $n$, kí hiệu $S(n)$ là tổng các chữ số của $n^2+1$.

Xây dựng dãy $(a_n)$ như sau: $a_0 \in \mathbb{N}$ nào đó. $a_{n+1}=S(a_n); \forall n \in \mathbb{N}$.

Chứng minh rằng dãy $a_n$ tuần nào từ một số hạng thứ $n_0$ nào đó, tức chứng minh rằng tồn tại $k,n_0 \in \mathbb{N}$ sao cho $a_{n+k}=a_n ; \forall n \ge n_0 $

Câu 3.b (mình Đóng góp một cách giải không sử dụng ý $a$)

Giả sử $k$ là một ước số của $a^n+b^n$ với mọi số nguyên dương $n>2016^{2017}$

Chọn $n>2016^{2017}$ sao cho $(p-1,n)$ với mọi $p$ là ước nguyên tố của $k$. (nếu thắc mắc về sự tồn tai điều này ta có thể với mỗi $p$ chọn một $n$ thỏa mãn điều này$

Khi đó không khó để chứng minh: $p$ là ước nguyên tố của $a+b$ 

Điều này chứng tỏ mọi ước nguyên tố $p$ của $k$ điều là ước nguyên tố của $a+b$.

Từ đây với mọi $p$ sử dụng chọn $n$ là số nguyên tố thì sử dụng bổ đều $LTE$ ta thu được $k$ là ước của $a+b$.

Phần tô đỏ các bạn có thể tham khảo Bổ đề của mình viết tại trang 71  Tạp chí $Epsilon$ số 7

Cho $X$ là không gian Metric và $B$ là tập con thực sự khác rỗng của $X$. 

a, Tồn tại hay không tập $B$ vừa mở, vừa đóng trong $X$.

b. Tồn tại hay không tập $B$ vừa mở, vừa đóng trong $X$ nếu $X$ là không gian định chuẩn?

Chứng minh không gian tích $XxY$ của hai không gian Metric là compact khi và chỉ khi X,Y là compact

 

Viết bdt đã cho dưới dạng thuần nhất

$\sum_{cyc} \frac{a+b}{\sqrt{a+b-c}} \ge 6\sqrt[4]{\frac{a^2+b^2+c^2}{3}}$

Do nó thuần nhất nên bỏ qua đk $a^2+b^2+c^2=3$ và chuẩn hóa $a+b+c=3$

$bdt\Leftrightarrow \sum_{cyc}\frac{3-a}{\sqrt{3-2a}} \ge 6\sqrt[4]{\frac{a^2+b^2+c^2}3}$

Với mọi $x \in \left(0; \frac 32\right)$ thì ta có $\frac{3-x}{\sqrt{3-2x}} \ge \frac{x^2+3}{2}$

Áp dụng bồ đề trên, ta thu được 

$VT \ge \frac{\left(a^2+b^2+c^2\right)+3+3+3}{2} \overset{AM-GM}\ge 2\sqrt[4]{3.3.3(a^2+b^2+c^2)}=VP$

$\color{red}{\text{Bài 41}} $(Tran Hoang Nam): Cho $\begin{cases}x,y,z \ge0 \\ x+y+z=3 \end{cases}$. Chứng minh $(x^2+2)(y^2+2)(z^2+5) \ge \frac{729}{16}$

 

Cách làm này bạn tham khảo ở đâu nhỉ? Đây chính là cách làm của mình cho bài này?

Bài 39 đã qua khá lâu nhưng chưa có lời giải. Mình xin được ra bài 40. Có một góp ý nhỏ, nếu quá thời gian quy định thì các bạn post bài nên post lời giải của mình nếu có để mọi người tham khảo.

Bài 40. Cho $a,b,c$ là độ dài ba cạnh của một tam giác thỏa mãn $a^2+b^2+c^2=3$. Chứng minh rằng:

            $\frac{a+b}{\sqrt{a+b-c}}+\frac{b+c}{\sqrt{b+c-a}}+\frac{c+a}{\sqrt{c+a-b}} \ge 6$

MẪU
Họ tên (Để ghi lên giấy chứng nhận): Nguyễn Văn Thế
Địa chỉ (Để ghi lên giấy chứng nhận): Lớp 12T1-Trường THPT Chuyên Hà Tĩnh
 

Nguyện vọng mua sách:

NV1: Reading for Ielts (Collins)

NV2: Nhập môn Lập Trình (Trần Đan Thư)

NV3: Kỹ Thuật Lập Trình (Trần Đan Thư

NV4: Phân tích và thiết kế giả thuật

NV5:

Địa chỉ nhận áo, GCN và phần thưởng: Nguyễn Văn Thế-Thôn 4- Xã Cẩm Trung-Huyện Cẩm Xuyên-Tỉnh Hà Tĩnh

Câu 5. Thực ra nó dấu ý ngũ giác khi cho các mặt phẳng, cũng như bài này.

Đề tuyển sinh Trường THPT Chuyên Hà Tĩnh năm 2013-2014 (Năm mình thi)

http://diendantoanho...13-2014-chuyên/

Câu 3:1 bài toán của thầy Nam Dũng,đã được thảo luận tại đây

Câu 5:Chém câu tổ không biết đã chuẩn chưa 

Xét bát giác đều $ABCDEFGH$

Xét theo 1 điểm bất kì nối 7  điểm còn lại,theo Dirichlet tồn tại 3 điểm có cùng màu.

Không mất tính tổng quát giả sử 3 điểm đó cùng màu đỏ.

Giả sử điểm đang xét là $A$ và 3 điểm màu đỏ là $B,C,E$,nếu $D$ màu đỏ ta có đpcm,giả sử $D$ màu xanh.

Gọi $O$ là tâm của bát giác nếu $O$ có màu đỏ ta có đpcm

Nếu $O$ màu xanh

+1 trong 4 điểm $A,H,G,F$ có màu xanh ta có đpcm

+Áp dụng định lý Dirichlet,tồn tại ít nhất 3 điểm có cùng màu đỏ hoặc vàng.

Giả sử $G,A$ màu đỏ thì tam giác $GEC,ABC$ là tam giác cần tìm

+Nếu $A,G$ màu vàng thì $H$ màu vàng ta có đpcm

+Nếu $H$ màu đỏ,gọi $I,J,K$ lần lượt là trung điểm của $FE,CD,AB$

+Khi đó $J,I$ màu vàng (nếu $J,I$ màu đỏ thì tam giác $BJE,IHC$ là tam giác cần tìm)

+Nếu $K$ màu đỏ thì tam giác $KAF$ là tam giác cần tìm

+Nếu $K$ màu vàng thì tam giác $KJI$ là tam giác cần tìm

Trường hơp $O$ màu vàng tương tự

sp1.JPG

Chưa chặt bạn ạ, bạn giải sử $B,C,E$ là không được rồi, vì nó phụ thuộc hình vẽ. Trường hợp này sẽ khác trường hợp kia.

Câu 5.

Câu 5.

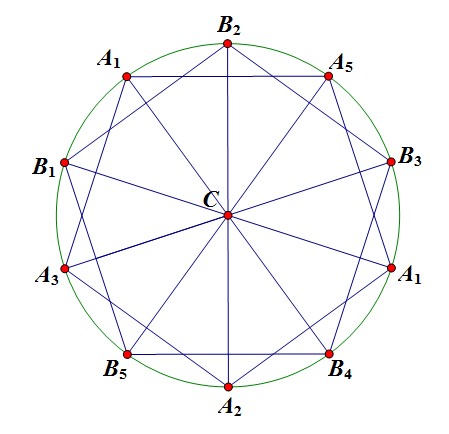
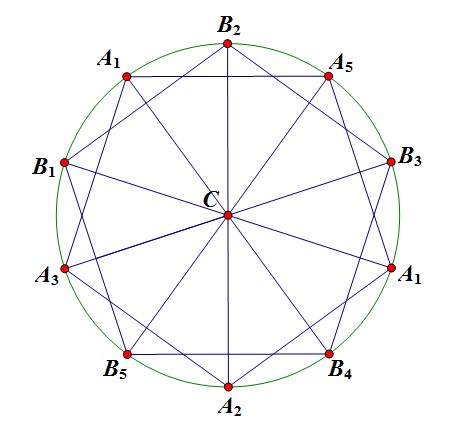
 Tính chất quen thuộc: 3 đỉnh bất kì của một ngũ giác đều thì tao giác một tam giác cân.

Ta xét một đường tròn tâm $C$. Trên đường tròn $(C)$ lấy ra 2 ngũ giác đều $ A_1A_2A_3A_4A_5$ và $B_1B_2B_3B_4B_5$.

Giả sử $C$ được tô xanh.

Khi đó nếu trong 10 điểm $ A_1,A_2,...,A_5,B_1,B_2,...,B_5$ cố 2 điểm được tô xanh thì ta có điều phải chứng minh.

Xét trường hợp trong 10 điểm chỉ có nhiều nhất 1 điểm được tô xanh. Khi đó trong 2 ngũ giác đều $ A_1A_2A_3A_4A_5$ và $B_1B_2B_3B_4B_5$ tồn tại 1 ngũ giác không có điểm xanh.

Giả sử $B_1B_2B_3B_4B_5$ không có điểm xanh, khi đó tồn tại 3 đỉnh trong ngũ giác đều này được tô cùng màu, từ đây ta có điều phải chứng minh. 

Câu 5. 

 Tính chất quen thuộc: 3 đỉnh bất kì của một ngũ giác đều thì tao giác một tam giác cân.

Ta xét một đường tròn tâm $C$. Trên đường tròn $(C)$ lấy ra 2 ngũ giác đều $ A_1A_2A_3A_4A_5$ và $B_1B_2B_3B_4B_5$.

Giả sử $C$ được tô xanh.

Khi đó nếu trong 10 điểm $ A_1,A_2,...,A_5,B_1,B_2,...,B_5$ cố 2 điểm được tô xanh thì ta có điều phải chứng minh.

Xét trường hợp trong 10 điểm chỉ có nhiều nhất 1 điểm được tô xanh. Khi đó trong 2 ngũ giác đều $ A_1A_2A_3A_4A_5$ và $B_1B_2B_3B_4B_5$ tồn tại 1 ngũ giác không có điểm xanh.

Giả sử $B_1B_2B_3B_4B_5$ không có điểm xanh, khi đó tồn tại 3 đỉnh trong ngũ giác đều này được tô cùng màu, từ đây ta có điều phải chứng minh. 

Ảnh