Lời giải của em (do lời giải em lấy nguyên xi từ bữa gửi tạp chí nên một số điểm không giống trong đề của thầy)

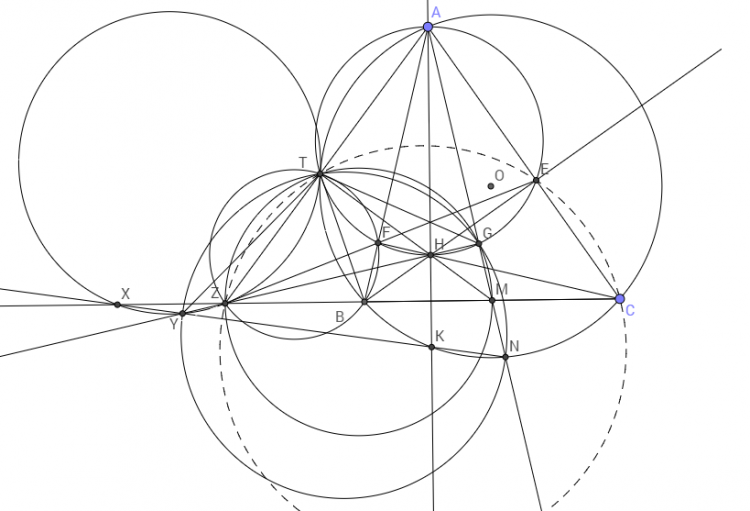
Trường hợp 1: Tam giác ABC cân, khi đó dễ dàng chứng minh được $\widehat{BAM}=\widehat{CAN}$

Trường hợp 2: Tam giác ABC không cân, giả sử $AB<AC$

Gọi $P,Q$ lần lượt là giao điểm của $\Delta$ với $AB,AC$, $X,Y$ lần lượt là giao điểm của $EM$ với $AB$, $AC$ với $FN$.

Ta có: $\widehat{EXB}=90^{\circ}-\widehat{EPX}=\widehat{\frac{A}{2}}=\widehat{FYC}$

Ta chứng minh $\frac{XM}{XA}=\frac{YN}{YA}$

$\Leftrightarrow \frac{XM}{MD}.\frac{MD}{XA}=\frac{YN}{ND}.\frac{ND}{YA}$

$\Leftrightarrow \frac{XM}{MD}=\frac{YN}{ND}$ (vì $\frac{MD}{XA}=\frac{BD}{BA}=\frac{CD}{CA}=\frac{ND}{YA}$)

$\Leftrightarrow \frac{XM}{YN}=\frac{MD}{ND} \Leftrightarrow \frac{BM.CD}{CN.BD}=\frac{IE}{IF}$ (vì $EM|| ID|| FN$ nên $\frac{MD}{DN}=\frac{IE}{IF}$)

$\Leftrightarrow \frac{BM}{CN}.\frac{IF}{IE}=\frac{AB}{AC}\Leftrightarrow \frac{BE}{IE}.\frac{IF}{CF}=\frac{AB}{AC}$ (có $\frac{BM}{CN}=\frac{BE}{CF}$ theo định lý Sin)

$\Leftrightarrow \frac{\sin \widehat{\frac{C}{2}}}{\cos \widehat{\frac{B}{2}}}:\frac{\sin \widehat{\frac{B}{2}}}{\cos \widehat{\frac{C}{2}}}=\frac{\sin \widehat{C}}{\sin \widehat{B}}=\frac{AB}{AC}$ (Đúng)

Do đó $\Delta AMX\sim \Delta ANY$ nên $\widehat{MAX}=\widehat{NAY}$

bạn ơi MN sao lại là trục đẳng phương của hai đường tròn kia được hả bạn

Bạn chứng minh tứ giác EIBD và FICD nội tiếp bằng biến đổi góc rồi suy ra phương tích nhé

Tình hình các bạn như thế nào nhỉ, mình làm xong câu 1 với câu 3 là hết giờ luôn rồi (làm đúng ý tưởng câu 2 mà hết giờ luôn )

Câu 3 mình làm thế này:

a) Chứng minh $MN$ là trục đẳng phương của đường tròn Euler với đường tròn $(O)$

b) Gọi $T$ là trung điểm $EF$, $L$ là trung điểm $BC$

Ta chứng minh tam giác $LBT$ đồng dạng tam giác $CDE$ (c-g-c) thì ra được $B,T,P$ thẳng hàng

Tương tự $C,T,Q$ thẳng hàng

Gọi $A'$ đối xứng $A$ qua $O$, để chứng minh $R,T,S$ thẳng hàng mình sử dụng định lý Thales chứng minh $\frac{LT}{A'S}=\frac{RL}{RA'}$

Ở đây biến đổi đại số bằng phương tích thôi

Bài 5 ngày 2 câu a dùng định lý Turan (định lí Turan xem ở đây: https://en.m.wikiped...Turán's_theorem)
câu b thì mình chưa nghĩ ra

Xét $n=2$, trường hợp này đơn giản, giả sử bài toán đúng đến $n=k$, ta chứng minh trường hợp $n=k+1$

Theo định lý Turan đồ thị $G$ này chứa ít nhất 1 tam giác (ý 1 của bài), $\Delta ABC$ chẳng hạn.

Không mất tính tổng quát giả sử $d(A)\leq d(B)\leq d(C)$. Ta sẽ xét đồ thị $G'$ không chứa đỉnh $A,B$, lúc này trong $G'$ có $2k$ đỉnh, tiếp theo nếu ta chứng minh được trong $G'$ có $\geq k^2+1$ cạnh nữa là đủ (mà điều này là tương đương với $f(A)+f(B)\leq 2k+1$, ở đây $f(A)$ là số đỉnh khác $A,B,C$ trong $G$ mà kề với $A$, $f(B),f(C)$ xác định tương tự)

Cuối cùng ta chỉ cần xét $S$ bằng tổng số các đỉnh trong $G$ kề chung $A$ với $B$, kề chung $B$ với $C$, kề chung  $C$ với $A$ mà khác $A,B,C$.

Nếu $S\geq k$ thì hiển nhiên suy ra đpcm (chú ý bổ sung tam giác $ABC$).

Nếu $S<k$ thì sẽ dẫn đến $f(A)+f(B)\leq 2k+1$ (bằng cách chứng minh $f(A)+f(B)+f(C)\leq 3k-2$ rồi dùng dữ kiện $d(A)\leq d(B)\leq d(C)$

Trùng hợp quá, thầy có ra bài này trong đống bài tập bồi dưỡng, ý tưởng thế này:
Gọi $I$ là tâm $(MNH)$, $O_1,O_2$ lần lượt là tâm $(AHC),(AHB)$ hạ $IE\perp OO_2, HF\perp OO_2,IE'\perp OO_1, HF'\perp OO_1$

$I,O,H$ thẳng hàng $\Leftrightarrow \frac{IE}{HF}=\frac{IE'}{HF'}$

Ngang đây thì biến đổi thôi (mình làm hơi dài, nhác gõ quá) 

Gọi $A',B',C'$ lần lượt là trung điểm của $BC,CA,AB$, $G$ là trọng tâm tam giác $ABC$

Phép vị tự tâm $G$ tỉ số $\frac{-1}{2}$ biến $A$ thành $A'$, $B$ thành $B'$, $C$ thành $C'$

Do đó phép vị tự này biến $D$ đối xứng với $A$ qua $BC$ thành $D'$ đối xứng với $A'$ qua $B'C'$, tương tự cho $E,F$

Để ý là $OA'\perp BC$ nên $D'$ là giao điểm của $OA'$ với đường thẳng qua $A$ song song $BC$

Ta kéo dài các đường thẳng qua $A,B,C$ lần lượt song song với $BC,CA,AB$ cắt nhau tạo thành tam giác $MNP$, khi đó $D',E',F'$ lần lượt là hình chiếu của $O$ lên $NP,PM,MN$

Mà $D,E,F$ thẳng hàng $\Leftrightarrow D',E',F'$ thẳng hàng $\Leftrightarrow O \in (MNP)$ (Đường thẳng $Simson$)

Để ý $H$ chính là tâm $(MNP)$ nên $OH=2R$

câu 1 làm sao

Bài 1 mình làm thế này:

Ta có: $|(x_{a+1}-x_a)-(x_{b+1}-x_b)|=|(x_{a+b+1}-x_a-x_{b+1})-(x_{a+b+1}-x_b-x_{a+1})|\leq |x_{a+b+1}-x_a-x_{b+1}|+|x_{a+b+1}-x_b-x_{a+1}|$

$<\frac{2}{a+b+1}$

Do đó:
$|(x_{m+1}-x_m)-(x_{n+1}-x_n)|=|(x_{m+1}-x_m)-(x_{a+1}-x_a)+(x_{a+1}-x_a)-(x_{n+1}-x_n)|<\frac{2}{a+m+1}+\frac{2}{a+n+1}$

Cho $a\rightarrow +\infty$ ta được $x_{m+1}-x_m=x_{n+1}-x_n=d$

Do đó $(x_n)$ là cấp số cộng

Bài 7 có thể tìm thấy trong cuốn Bồi dưỡng học sinh giỏi toán tổ hợp rời rạc của thầy Nguyễn Văn Thông nhé (có thể dùng hàm sinh để giải )

Bài 3a dùng $\mod 2$ như trong link của Bảo, câu b ta đặt giá trị của con ong tương ứng với giá trị của cây mà con ong đó đang đậu, khi đó dễ thấy tổng giá trị tất cả con ong là bất biến và bằng $n(2n-1)$ trong TH tổng quát $2n-1$ cây, nếu có $n$ con ong đậu ở cây $2n-1$ thì tổng sẽ $>n(2n-1)$ (vô lý)

Câu 3: 

Theo tính chất quen thuộc thì $E,F,Z$ thẳng hàng.

Gọi $T$ là điểm $Miquel$ của tứ giác toàn phần $BFECZA$, ta sẽ chứng minh $XYZT$ là tứ giác nội tiếp.

Dễ dàng chứng minh $M,H,T$ thẳng hàng, suy ra $MGTZ$ là tứ giác nội tiếp.

Mặt khác có $\widehat{TNY}=\widehat{TNK}=\widehat{TAK}=\widehat{TAH}=\widehat{TGH}=\widehat{TGY}$ nên tứ giác $TGNY$ là tứ giác nội tiếp.

Suy ra $T$ cũng là điểm $Miquel$ của tứ giác toàn phần $YZMNXG$ nên tứ giác $XYZT$ nội tiếp.

Để chỉ ra 2 đường tròn $(XYZT)$ và $(O)$ tiếp xúc tại $T$ ta chỉ cần chứng minh $\widehat{BTZ}=\widehat{TYZ}+\widehat{TAB}$ $(*)$

Mà $\widehat{TYZ}=\widehat{TNA}=\widehat{TBA}$ nên hiển nhiên $(*)$ đúng.

Vậy 2 đường tròn $(XYZ)$ và $(O)$ tiếp xúc nhau.

Câu 4: Một tập hợp các số nguyên dương được gọi là tập hương nếu tập đó có ít nhất 2 phần tử và mỗi phần tử của nó có ước nguyên tố chung với ít nhất một trong các phần tử còn lại. Đặt $P(n)=n^2+n+1$. Hãy tìm số nguyên dương $b$ nhỏ nhất sao cho tồn tại số nguyên không âm $a$ để cho tập hợp 

$$\{P(a+1),P(a+2),...,P(a+b)\}$$

là một tập hương.

Lời giải:

Xét trường hợp $b\leq 5$, sử dụng thuật toán Euclid với lưu ý rằng $P(n)$ không chia hết cho $2$ ta có:

$$gcd(P(a+1),P(a+2))=1$$

$$gcd(P(a+1),P(a+3))|7$$

$$gcd(P(a+1),P(a+4))|3$$

$$gcd(P(a+1),P(a+5))|19$$

Cụ thể hơn, $gcd(P(a+1),P(a+3))=7$ tương đương với $a+1\equiv 2 (\mod 7)$, $gcd(P(a+1),P(a+4))=3$ tương đương với $a+1\equiv 1 (\mod 3)$, $gcd(P(a+1),P(a+5))=19$ tương đương với $a+1\equiv 7 (\mod 19)$

Do đó các ước nguyên tố chỉ có thể nằm trong tập hợp $\{3,7,19\}$

Xét một mặt phẳng và 5 điểm $A_1,A_2,...,A_5$ tương ứng với 5 giá trị của $P(a+1),P(a+2),...,P(a+5)$, $A_k$ và $A_l$ được nối với nhau bởi 1 đoạn thẳng có độ dài $3,7,19$ tương ứng với ước nguyên tố chung của $P(a+k)$ và $P(a+l)$ ($A_i$ không thể nối với $A_{i+1}$).

Trường hợp $b=5$:

Nếu $A_1$ nối với $A_5$, khi đó $A_2$ nối với $A_4$ và $A_3$ nối với $A_1$ hoặc $A_5$ (vô lý)

Nếu $A_1$ nối với $A_3$ thì $A_2$ nối với $A_4$ (loại) nên $A_2$ nối với $A_5$, khi đó $A_4$ phải nối với $A_1$, $a$ phải thỏa mãn:

$a\equiv 6 (\mod 7); a\equiv 2 (\mod 3); a\equiv 0 (\mod 3)$ vô lý.

Nếu $A_1$ nối với $A_4$ thì $A_2$ nối với $A_5$ cũng vô lý.

Vậy trường hợp này loại.

Tương tự, ta xét các trường hợp $b=2,3,4$ còn lại suy ra $b\geq 6$

Trường hợp $b=6$, sử dụng định lý Thặng dư Trung Hoa cho hệ sau:

$$a+1\equiv 7 (\mod19)$$

$$a+2\equiv 2 (\mod 7)$$

$$a+3\equiv a+6\equiv 1 (\mod 3)$$

$$a+4\equiv 4 (\mod 7)$$

$$a+5\equiv 11 (\mod 19)$$

Từ đó suy ra $b=6$ là giá trị nhỏ nhất cần tìm

Bài hình P1 khá thú vị. Mình xin gửi lại hai mở rộng cho bài 1 mình đã post trên AoPS như sau

 

Bài toán 1a. Cho tam giác $ABC$ có $\angle ABC$ tù và tâm ngoại tiếp $D$. Trung trực $AB$ cắt $AC$ tại $F$. $E,M$ là tâm ngoại tiếp tam giác $ADF,BFC$. Dựng hình bình hành $AMXE$. Chứng minh rằng $EM,FX,BD$ đồng quy.

 

Figure3959.png

 

Bài toán 1b. Cho tam giác $ABC$ tâm ngoại tiếp $O$. Trung trực của $AB,AC$ cắt $BC$ tại $F,E$. Gọi $K,L,M,N$ là tâm ngoại tiếp các tam giác $BFD,CDE,AFC,AEB$.

 

a) Chứng minh rằng $KM,LN,AO$ đồng quy.

 

b) Chứng minh rằng $KL$ vuông góc với đường thẳng Euler của tam giác $ABC$.

 

Figure3960.png

Em xin giải mở rộng của thầy

Bài toán $1a$: Ta có: $\widehat{BDF}=\frac{1}{2}\widehat{BDA}=\widehat{BCA}$ nên tứ giác $BCDF$ nội tiếp đường tròn tâm $M$

Hai tam giác $ADF$ và $BDF$ đối xứng nhau qua $DF$ nên $E$ đối xứng $M$ qua $DF$

Lại có $MF=MD$ nên $ME$ là đường trung trực của $FD$. Do đó phép đối xứng qua trung điểm của $DF$ biến $A$ thành $X$ hay $ADXF$ là hình bình hành.

$\Rightarrow \widehat{FXD}=\widehat{FAD}=\widehat{FBD}$ hay $BFDX$ nội tiếp đường tròn $(M)$, cũng dễ dàng chứng minh được $FD|| BX$ nên $FDXB$ là hình thang cân.

$ME$ là đường trung trực của $FD$ nên hiển nhiên $ME$ đi qua giao điểm của $XF$ và $BD$

Câu $b$ của thầy chắc là $BFO,COE$ thay vì $BFD,CDE$ chứ ạ

Theo câu $a$ thì $KM,LN$ lần lượt là trung trực của $OF,OE$, do đó để chứng minh $KM,LN,AO$ đồng quy thì ta cần chứng minh $AO$ đi qua tâm đường tròn ngoại tiếp tam giác $OEF$

Ta có $\widehat{AOF}=\widehat{C}=\widehat{EOH}$ với $H$ là chân đường vuông góc hạ từ $O$ xuống $BC$ nên $OA, OH$ đẳng giác

Suy ra đpcm

Ý $b$ chỉ cần biến đổi góc là ra: $BH\cap (K)=X, CH\cap (L)=Y$ ta có:

$\widehat{XOY}=\widehat{XOF}+\widehat{FOE}+\widehat{EOY}=\widehat{HBC}+\widehat{BHC}+\widehat{HCB}=180\circ$ nên $X,O,Y$ thẳng hàng.

Tiếp tục xét tứ giác $XBYC$ thì dễ dàng chứng minh được $\widehat{BXY}=\widehat{YCB}$ nên tứ giác $XBYC$ nội tiếp

Do đó $HB.HX=HC.HY$ nên $H$ thuộc trục đẳng phương của 2 đường tròn $(K),(L)$.

Suy ra $HO\perp KL$ 

câu đó bạn làm sao vậy ???? Chả lẽ góc $54^0$ là góc đặc biệt à chứ nghe nói là không thể chia 3 1 góc bằng thước thẳng và compa được

Mình làm khá vớ vẩn: Từ điểm $A$ lấy trên tia $Ax$ một điểm $O$, vẽ đường tròn bán kính $OA$, qua $O$ vẽ đường vuông góc với $OA$ cắt đường tròn tại 2 điểm $B,C$ (lấy $B$ ở dưới tia $Ox$), lấy $M$ là trung điểm của $OB$ rồi vẽ đường tròn bán kính $MA$ cắt $OC$ tại $E$. Lấy $A'$ là điểm đối xứng của $A$ qua $O$ rồi vẽ đường tròn bán kính $A'E$ cắt $(O)$ tại $K$. Nối $AK$ rồi dựng tia phân giác góc $\widehat{KAx}$

Ai tới phần 7 eta câu đầu chưa. làm sao vẽ được cái hình vuông đó

Mình dựng thế này

Cho tam giác ABC, trọng tâm $G$.

$A_1,B_1,C_1$ là hình chiếu $G$ lên $BC,CA,AB$.

$A_2,B_2,C_2$ đối xứng $A_1,B_1,C_1$ qua $G$.

CM: $AA_2,BB_2,CC_2$ đồng qui.

Bài này dùng phép chiếu Vecto giải được nhưng khá dài với "dễ nghĩ quá", hóng cách thuần túy.

Chứng minh: $\text{C}_{2n+1}^{n}\vdots 2n+1$

Cái này trích ra từ câu $T10/466$ à Đớ, thực ra thì mấu chốt câu nớ dùng bổ đề $LTE$ với định lý $Legendre$ là ra, bước đánh giá ở chỗ phần nguyên hơi "khắm"

Bài 6:

Câu $a)$ là tầm thường, mình xin giải câu $b)$

Ta sẽ chứng minh để các quân cờ $L-Tetromino$ phủ kín hết bàn cờ thì $8|n^2$ hay $4|n$

Thật vậy, giả sử hình vuông $n^2$ được phủ kín bởi các quân cờ đó, vì số ô vuông của quân $L-Tetromino$ là $4$ nên số ô vuông của bàn cờ phải có dạng $n^2=4m$ ($m\in N$) tức là $2|n$. Ta tô như hình vẽ dưới:

Với mỗi cách tô trên thì hoặc quân cờ $L-Tetromino$ chứa $3$ ô đen $1$ ô trắng (loại $1$) hoặc $L-Tetromino$ chứa $1$ ô đen $3$ ô trắng (loại $2$). Do đó mỗi quân cờ có số ô đen, trắng hơn kém nhau $2$ mà để phủ hết bàn cờ thì số ô đen, trắng phải bằng nhau, dẫn đến $L-Tetromino$ loại $1$ bằng loại $2$ tức là $2|m$. Vậy $n^2=8k$ ($k=\frac{m}{2}$)

Bây giờ ta chứng minh khi $n$ chia hết cho $4$ thì luôn ghép các quân $L-Tetromino$ phủ kín bàn cờ được. Mà điều này dễ dàng chứng minh do $a)$

 

Câu 2(2đ)

a, Tính giá trị biểu thức $P=\frac{1}{2x+2xz+1}+\frac{2xy}{y+2xy+10}+\frac{10z}{10z+yz+10}$; với x,y,z là các số thoả mãn xyz = 5 và biểu thức P có nghĩa

b, Trong kì thi tuyển sinh vào lớp 10, có 112 thí sinh đăng kí dự thi vào lớp Chuyên Tin, giả sử mỗi thí sinh quen ít nhất 75 bạn trong 112 thí sinh này. CMR: luôn chọn đuợc 1 nhóm có 4 thí sinh mà hai bạn nào trong nhóm cũng quen nhau.

 

Trong mặt phẳng, ta quy ước mỗi thí sinh là một điểm và $2$ thí sinh quen nhau ta quy ước là một đoạn thẳng nối giữa $2$ điểm tương ứng với $2$ thí sinh đó.

Bây giờ ta giả sử $M$ và $N$ là 2 điểm đã được nối với nhau. Gọi $A$ là tập hợp các điểm nối với $M$ và $B$ là tập hợp các điểm nối với $N$ (tập $A$ không chứa $N$, tập $B$ không chứa $M$).

Ta có: $|A\cap B|=|A|+|B|-|A\cup B|\geq 2.75-112=38>0$ do đó $M$ và $N$ cùng nối chung đến một điểm $P$ nào đó.

Gọi $C$ là tập hợp các điểm nối với $P$, khi đó $|C|\geq 75$.

Do đó từ $112\geq |(A\cap B)\cup C|=|A\cap B|+|C|-|A\cap B\cap C|$ suy ra $|A\cap B\cap C|\geq 38+75-112=1$

Vậy tồn tại $Q\in |A\cap B\cap C|$ tức là tồn tại 1 nhóm có 4 thí sinh mà 2 bạn trong nhóm quen nhau. 

Câu 5:

a) Dễ thấy rằng tổng của tất cả các số thuộc các tập $A_i$ phải là số chẵn mà $1+2+3+...+93=4371$ là số lẻ nên ta có ĐPCM

b) Ta sẽ chia thành các bộ số như sau (mỗi bộ số tương ứng với một tập $A_i$):

$(415,416,831);(413,417,830);(411,418,829);...;(1,623,624)$

Còn lại các số: $2,4,6,...,414$ chưa thuộc tập $A_i$ nào, lại thấy yêu cầu rằng tổng $2$ số bằng số thứ $3$ trong tập $A_i$ bất kì nên việc sắp các số $2,4,6,...,414$ vào tập $A_i$ cũng tương ứng với sắp các số $1,2,3,...,207$ vào các tập $B_j$ thỏa mãn trong $B_j$ có $1$ số bằng tổng $2$ số còn lại.

Ta tiếp tục chia như sau:

$(103,104,207),(101,105,206),(99,106,205),...,(1,155,156)$

Tương tự như trên, ta lại sắp các số $1,2,3,...,51$ như sau:

$(25,26,51),(23,27,50),(21,28,49),...,(1,38,39)$

Cuối cùng, ta sắp các số $1,2,...,12$ như sau:

$(1,5,6);(2,9,11),(3,7,10),(4,8,12)$

Bài toán được chứng minh 

mà nghĩ cũng lạ, học toán giỏi thì dốt văn, ai trả lời giùm em câu này.(mai thi rồi mà chả có một chữ văn , cầu mong ra thơ việt nam) 

Theo kinh nghiệm của bản thân anh hơn $90%$ dân chuyên toán là giỏi Văn nghị luận xã hội em nhé

dạ e thi chuyên quảng bình thôi ạ . van hoi ngu nen ko giam thi quoc hoc

Mỗi Văn ngu thì có gì phải sợ, hồi lớp 9 anh đây Văn Anh max ngu, điểm Văn $3,75$ còn Anh $4,8$ thế mà vẫn đậu lớp Toán 1

Nhớ lại thì hồi đó thi Văn mà không chịu học thuộc thơ, thế là cả bài văn $4,5$ điểm gì đấy ngậm bút không biết viết cái gì, mà Văn mình vào đó cũng không bằng một nửa họ, chúng nó chém $3$ tờ giấy trong $90$ phút, mình "rặn" mãi $3$ mặt giấy mà hết $60$ phút rồi, $30$ phút còn lại ngồi ngắm trường

nói chung là cũng phải học . lớn lên rồi tính tiếp

Em định thi chuyên Quảng Bình hay Quốc Học thế

Tồn tại hay không sô nguyên $n$ thỏa mãn $n$ có đúng $2000$ ước nguyên tố và $2^n+1$ chia hết cho $n$.  $(*)$

Ta sẽ chứng minh bằng quy nạp theo $k$ $(k\in N^*)$ rằng luôn tồn tại số nguyên $n_k$ có $k$ ước nguyên tố (trong đó có $3$) thỏa mãn $2^{n_k}+1$ chia hết cho $n_k$.

Với $k=1$ cho $n_1=3$ hiển nhiên $(*)$ đúng. Giả sử $(*)$ đúng đến $k=i$ tức là $n_i|2^{n_i}+1$.

Khi đó: $3n_i|2^{3n_i}+1=(2^{n_i}+1)(2^{2n_i}-2^{n_i}+1)$ (vì $n_i$ phải là số lẻ dẫn đến $3|2^{2n_i}-2^{n_i}+1$)

Để ý rằng luôn tồn tại số nguyên tố $p$ là ước của $a^3+1=(a+1)(a^2-a+1)$ (với $a=2^{n_i}\geq 8$) mà không phải là ước của $(a+1)$. Thật vậy, thấy rằng $(a+1,a^2-a+1)=(a+1,3)$ mà $3|n_i|2^{n_i}+1$ nên $3|a+1$, tức $(a+1,a^2-a+1)=3$, đặt $a=3b-1$ thì $a^2-a+1=9b^2-9b+3$ không chia hết cho $9$, vì thế ta có thể lấy bất kì số nguyên tố $p$ nào là ước của $\frac{a^2-a+1}{3}>3$.

Đặt $n_{i+1}=3pn_i$ thì hiển nhiên $n_{i+1}=3pn_i|2^{3pn_i}+1=2^{n_{i+1}}+1$

Vậy theo nguyên lý quy nạp ta có điều phải chứng minh.

Bài toán 10: Một tập hợp A các số tự nhiên được gọi là hoàn hảo nếu thoả mãn đồng thời 3 điều kiện sau:

(i) 0∈A

(ii) Nếu a∈A thì a+2015∈A

(iii) Nếu a∈A thì a+2016∈A

Hỏi có tất cả bao nhiêu tập hoàn hảo?

c) $AH\cap BC=D$

Xét đường tròn $(I,IA)$ có tam giác $IEF$ cân. Do đó $\widehat{IEH}=90^{\circ}-\widehat{A}=\widehat{ABE}$ nên $IE$ tiếp xúc với đường tròn $(M,MB)$.

Bây giờ giả sử $IC\cap (M)=L$ thì $\widehat{BLC}=90^{\circ}$. Ta sẽ chứng minh $\widehat{KLC}=90^{\circ}$.

Vì $IE$ tiếp xúc đường tròn $(M)$ nên $IE^2=IL.IC$.

Mặt khác: $IK.ID=IE^2$ (dễ dàng chứng minh bằng tam giác đồng dạng)

Do đó $KLCD$ nội tiếp nên $\widehat{KLC}=90^{\circ}$.

d) $EQMC$ nội tiếp nên $\widehat{AQE}=\widehat{C}=\widehat{AFE}$.

Do đó $AFQE$ nội tiếp hay $AFHQE$ nội tiếp.

Suy ra $\widehat{AQH}=90^{\circ}$  $(1)$

Mặt khác gọi $J$ là trung điểm của $HM$ thì vì $EFMD$ nội tiếp (đường tròn $Ơ-le$) nên $PF.PE=PD.PM$ hay $P$ có cùng phương tích với $(I,IA)$ và $(J,JM)$ nên $PH\perp IJ$ dẫn đến $PH\perp AM$  $(2)$

Từ $(1)$ và $(2)$ suy ra ĐPCM

$AS$ cắt $(APQ)$ tại $H'$ thì vì $AS$ là đường đối trung của tam giác $APQ$ nên $\widehat{PAH'}=\widehat{BAQ}$ (vì $AB$ cắt $PQ$ tại trung điểm $PQ$, có thể dùng phương tích để chứng minh).

Mặt khác $\widehat{PAH'}=\widehat{PQH'}$ và $\widehat{BQP}=\widehat{BAQ}$ nên $\widehat{H'QP}=\widehat{BQP}$

Tương tự thì $\widehat{BPQ}=\widehat{H'PQ}$.

Từ đó suy ra $B$ và $H'$ đối xứng nhau qua $PQ$ dẫn đến ĐPQM

Tam giác nhọn $ABC$ nội tiếp trong đường tròn $(O)$.

$P$ là điểm nằm trong tam giác thỏa $\widehat{PAB}=\widehat{PBC}$ và $\widehat{PAC}=\widehat{PCB}$.

Lấy $Q$ trên $BC$ sao cho $QA=QP$.

Chứng mình rằng: $$\widehat{QAP}=2\widehat{OQB}$$

Đề đúng phải là chứng minh $\widehat{AQP}=2\widehat{OQB}$ chứ nhỉ.

Thực ra lời giải bài toán này khá đơn giản

Gọi $I,J$ lần lượt là tâm đường tròn ngoại tiếp tam giác $APB$ và $APC$ thì $Q,I,J$ thẳng hàng.

Để ý rằng điều kiện $\widehat{PAB}=\widehat{PBC}$ dẫn đến $(I)$ tiếp xúc với $BC$, tương tự thì $(J)$ tiếp xúc $BC$.

Dễ thấy $OI,OJ$ lần lượt là trung trực của $AB,AC$.

Ta có: $\widehat{OIJ}=\frac{1}{2}\widehat{AIB}-\widehat{AIJ}=\widehat{BIJ}-\widehat{OIJ}-\widehat{ABP}=2\widehat{BAP}-\widehat{OIJ}$

Do đó $\widehat{OIJ}=\widehat{BAP}=\widehat{PBC}$

Tương tự $\widehat{OJI}=\widehat{PCB}$

Vì thế nên $\Delta OIJ\sim \Delta PBC$

Mặt khác phép vị tự tâm $Q$ biến $I$ thành $J$ thì biến $B$ thành $C$ nên $\Delta OQJ\sim \Delta PQC$

Suy ra: $\widehat{PQB}=\widehat{OQI}$.

Từ đó suy ra điều phải chứng minh.