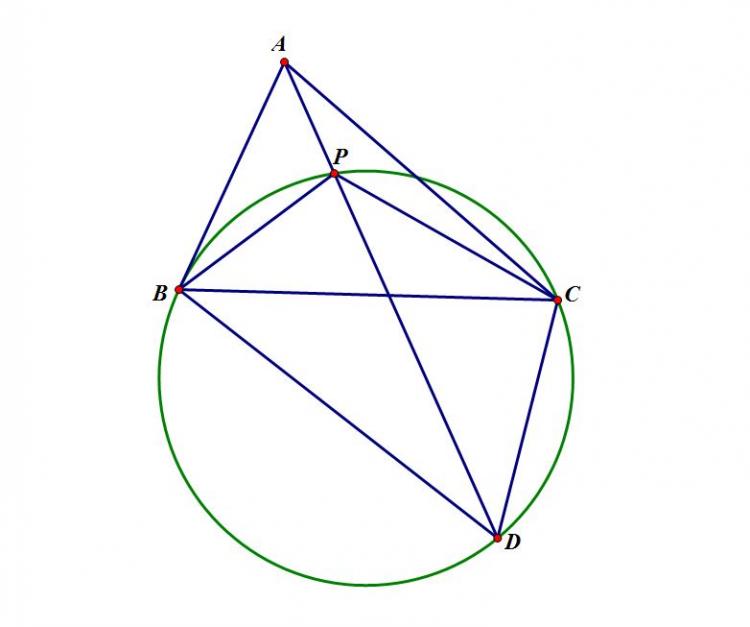
Trong lúc khảo sát trường hợp suy biến của Bài 1 ($BC=DE=0$) thì em có một quan sát như sau:

Gọi $P$ là điểm di động trên cung nhỏ AD của đường tròn ngoại tiếp hình thang cân $ABCD$ ( $AB=CD$ ). $PC$ giao $BD$ tại $N$, $PB$ giao $AC$ tại $M$. $K$ và $L$ lần lượt là hình chiếu của $M,N$ lên $AD$. $NK$ giao $ML$ tại $Q$. Khi đó $PQ$ qua điểm cố định.

Với điều kiện $AB=BC=CD$ thì điểm cố định là trung điểm $BC$.

 

Bài 1: Tìm đa thức $P(x)$ khác đa thức không sao cho $[P(x)]^n=P(x^n)$ với $\forall x\in\mathbb R$ và $n\ge 1$.

 

Bài 2: Có bao nhiêu số tự nhiên có 10 chữ số khác nhau trong đó các chữ số $1,2,3,4,5$ được sắp xếp theo thứ tự đó từ trái qua phải nhưng các số $1,2,3,4,5,6$ thì không.

 

Bài 1

Từ điều kiện trên suy ra hệ số bậc cao nhất của $P$ là 1.$deg(P)=k,deg(Q)=t,t<k$ với 

$P=x^{k}+Q$

Thay vào đẳng thức đã cho:

$(x^{k}+Q(x))^{n}=x^{kn}+Q(x^n)$

Triệt tiêu $x^{kn}$ ở hai vế:

$\sum_{i=1}^{n-1}\binom{n}{i}(x^k)^i[Q(x)]^{n-i}=Q(x^n)-[Q(x)]^n$

Mọi hạng tử ở vế trái đều có bậc có dạng $t(n-i)+ki=nt+(k-t)i> nt$

Vế phải có bậc $\leq nt$

Suy ra $Q$ là hằng số. Thử lại suy ra $Q$ đồng nhất $0$. 

Vậy $P=x^k$ với $k$ nguyên dương tùy ý

Bài 2

Có $\binom{10}{6}$ vị trí cho bộ các số từ 1 tới 6. Trong đó có:

• $\binom{9}{6}$ vị trí không chứa hàng đầu tiên của số có 10 chữ số. Còn lại 4 chữ số ${0,7,8,9}$ có $3.3.2.1$ cách xếp
• $\binom{9}{5}$ vị trí chứa hàng đầu tiên của số có 10 chữ số. Còn lại ${0,7,8,9}$ có $4!$ cách xếp

Trong mỗi vị trí của bộ 6 nói trên thì số 6 không đứng cuối cùng, nên có 5 khả năng cho số 6. Còn lại các số từ 1 tới 5 thì đã xác định với mỗi khả năng của 6.

Kết luận: Có $(\binom{9}{6}.3.3.2.1+\binom{9}{5}.4!).5$ số có 10 chữ số thỏa mãn

Em muốn trao đổi thêm về bài 165. Vì em có một vài suy luận dẫn đến kết quả sai nhưng chưa tìm ra chính xác lỗi sai ở đâu

Giả sử $\frac{AP}{AQ}=\frac{BP}{BQ}\Rightarrow \frac{sinABP}{sinBAP}=\frac{sinABQ}{sinBAQ}\Rightarrow \frac{sinABP}{sinBAP}=\frac{sinCBP}{sinCAP}$

Kết hợp với định lý Ceva dạng lượng giác cho tam giác $ABC$ có $AP,BP,CP$ đồng quy thì suy ra $sinPCA=sinPCB$, dẫn tới $P,Q,C$ thẳng hàng

Vậy nếu quả thực 3 tỉ số đã nói bằng nhau thì $AC$ sẽ là phân giác (trong hoặc ngoài) của tam giác $APQ$. $AI$ là đường phân giác trong cũng của tam giác này. Dẫn đến $AI$ vuông góc $AC$ hoặc $AI$ trùng $AC$. Cả hai khả năng này đều không khả thi.

Bài toán 160. Cho tam giác $ABC$ với đường tròn nội tiếp $(I)$ tiếp xúc các cạnh $BC,CA,AB$ lần lượt tại $D,E,F$. Gọi $\omega _1,\omega_2,\omega_3$ là các đường tròn nội tiếp của các tam giác $AEF$, $BDF$, $CDE$. Tâm nội tiếp $DEF$ là $J$. $G$ là trọng tâm của tam giác pedal của $J$ đối với tam giác $DEF$. Gọi:
$l_1,l_2,l_3,l_4$ là các tiếp tuyến chung của $\omega_2,\omega_3;$
$m_1,m_2,m_3,m_4$ là các tiếp tuyến chung của $\omega_1,\omega_3;$
$p_1,p_2,p_3,p_4$ là các tiếp tuyến chung của $\omega_1,\omega_2.$
Chứng minh rằng có thể lần lượt chọn trong các bộ $l_i,m_i,p_i(i=\overline{1,4})$ 3 đường $l,m,p$ sao cho $l,m,p,GI$ đồng quy.

Em có một ý tưởng khác cho bài 158

Giả sử $ABCD$ là tứ giác lồi và điểm $M$ nằm trong tứ giác, đồng thời có hình vẽ như bên dưới. Các trường hợp khác chứng minh tương tự. Gọi $O$ là tâm ngoại tiếp đường tròn đi qua 4 điểm.

Gọi $X,Y,Z,T$ là đối xứng của $O$ qua các cạnh liên tiếp của tứ giác $ABCD$. Cho điểm $M$ trùng với $O$ thì có thể dự đoán điểm cố định chính là giao điểm của $XZ$ và $YT$. Cũng dễ thấy $XYZT$ là hình bình hành nên 2 đường chéo cắt nhau tại trung điểm $S$.

Vậy ta chứng minh đường thẳng đi qua trung điểm $P_{ab}P_{cd}$ và S sẽ song song với đường thẳng qua trung điểm $P_{bc}P_{ad}$ và $S.$

Đặt lại tên các điểm như hình vẽ dưới.

$\vec{PQ}$ cùng giá với $\vec{KX}+\vec{HZ}$, hay cùng giá với phân giác góc tạo bởi 2 đường $KX$ và $HZ$ do $KX=MO=HZ$ 

Ta dựng thêm một đường phân giác tương tự. 

Việc còn lại chỉ là chứng minh hai đường phân giác này song song với nhau. Việc này có lẽ là đơn giản vì ta đã có cặp $AB,CD$ đối song với hai đường $AD,BC$, cũng như các đoạn đối xứng với $OM$ qua các cạnh ?

Lời giải bài toán 156

Xét tam giác $DBC$. Đặt $cotD=-cotBPC=\alpha$ ; $cotB=-cotAPC=\beta$ ; $cotC=-cotAPB=\gamma$

Kí hiệu $M(x:y:z)$ với điểm $M$ thỏa mãn $x\vec{MD}+y\vec{MB}+z\vec{MC}=0$

Và $d(X:Y:Z)$ với đường thẳng $d$ chứa những điểm có tọa độ $(x:y:z)$ sao cho $Xx+Yy+Zz=0$

Gọi $H$ và $G$ luần lượt là trực tâm và trọng tâm tam giác $DBC$. Ta có

$H(\alpha :\beta :\gamma ), G(1:1:1)$ suy ra đường thẳng Euler $HG(\beta -\gamma :\gamma -\alpha :\alpha -\beta )$

Lại có $BC(1:0:0)$ nên $X=BC\cap HG=(0:\alpha -\beta :\alpha -\gamma )$

Viết lại: $\vec{XB}(\alpha -\beta )+\vec{XC}(\alpha -\gamma )=0$ 

Hay $\vec{XB}(cotBPC-cotAPC)+\vec{XC}(cotBPC-cotAPB)=0$

Thiết lập các đẳng thức tương tự với tam giác $EAC$ và $FAB$, theo định lý Menelaus ta có điều phải chứng minh. 

cho các số thực dương a,b,c và abc=1 CMR$(a-1+\frac{1}{b})(b-1+\frac{1}{c})(c-1+\frac{1}{a})\leq 1$

Đặt $a=\frac{x}{y},b=\frac{y}{z},c=\frac{z}{x}$ ta đưa về bài toán quen thuộc là $(x+y-z)(y+z-x)(x+z-y)\leq xyz$

#IMO2000

Lời giải bài toán 150

Áp dụng định lý Ceva dạng lượng giác cho tam giác $ABC$ có $CP$, $AD$ và $BE$ đồng quy ta thu được:

$\frac{sinCAD}{sinDAB}=\frac{sinCBE}{sinABE}$

suy ra:

$\frac{sinADM}{sinDAM}=\frac{sinBEM}{sinEBM}$

theo định lý sin thì suy ra :

$\frac{AM}{MD}=\frac{BM}{ME}$

Vì $M$ là trung điểm $AB$ nên ta có điều phải chứng minh.

Thầy Hùng đề nghị bài mới giúp em nhé

Lời giải bài 144

Gọi $L_1, L_2, L_3$ là điểm Lemoine các tam giác $AEF,BDF,EDC$

Để ý rằng $EF=a cosA$, $AE=c cos A$, $AF=b cosA$ và các đẳng thức tương tự, ta có các đẳng thức vector sau:

$a^{2}\vec{LA}+b^{2}\vec{LB}+c^{2}\vec{LC}=0$

$a^{2}\vec{L_{1}A}+b^{2}\vec{L_{1}E}+c^{2}\vec{L_{1}F}=0$

$a^{2}\vec{L_{2}D}+b^{2}\vec{L_{2}B}+c^{2}\vec{L_{2}F}=0$

$a^{2}\vec{L_{1}D}+b^{2}\vec{L_{1}E}+c^{2}\vec{L_{1}C}=0$

Suy ra

$(a^2+b^2+c^2)(\vec{LL_{1}}+\vec{LL_{2}}+\vec{LL_{3}})+(a^2\vec{LA}+b^2\vec{LE}+c^2\vec{LF})+(a^2\vec{LD}+b^2\vec{LB}+c^2\vec{LF})+(a^2\vec{LD}+b^2\vec{LE}+c^2\vec{LC})=0$

Vậy ta cần chứng minh:

$a^2\vec{LD}+b^2\vec{LE}+c^2\vec{LF}=0$

hay

$a^2\vec{AD}+b^2\vec{BE}+c^2\vec{CF}=0$

Đẳng thức này đúng nên $\vec{L_{1}L}+\vec{L_{2}L}+\vec{L_{3}L}=0$

Ta có đpcm.

Giả sử có một số $a_{j}$ nào đó không nhỏ hơn 4.

Khi đó $a_{j}!-1$sẽ có ước nguyên tố dạng $4k+3$. Do đó $4k+3|3\Rightarrow 4k+3=3$ và $9|\prod_{i=1}^{n}(a_{i}!-1)$.

Ta chỉ cần tìm các số $a_{i}$ nhỏ hơn 6 sao cho $9|a_{i}!-1$. Vậy cần xét các số $a_{i}$ chạy từ 3 đến 5.

Mà dễ thấy $3!-1$, $4!-1$ và $5!-1$ đều không chia hết cho 3 nên bài toán vô nghiệm trong trường hợp này.

Còn nếu tất cả các số $a_{i}$ đều nhỏ hơn 4, có thể lí luận để dẫn tới $2-9=-7$ là số chính phương (sai).

Vậy bài toán vô nghiệm.

Câu 3, ngày 1:

Ta viết lại các đa thức $Q(x)$ dưới dạng: $Q_{i,j}=2x^{2}+(b_{i}+b_{j})x+(c_{i}+c_{j})$

Từ giả thiết suy ra $(b_{i}+b_{j})^{2}=8(c_{i}+c_{j}),\forall i,j$

Giả sử $n\geq 4$. Khi đó tồn tại bốn chỉ số $i,j,m,n$ phân biệt. Ta cũng có $(b_{m}-b_{n})(b_{m}+b_{n}+2b_{i})=8(c_{m}-c_{n})$. Do đó để các đa thức $P$ đã cho ban đầu là phân biệt thì $b_{i}\neq b_{j}$ nếu $i\neq j$

Mà ta lại có $8(c_{m}-c_{n})=(b_{m}-b_{n})(b_{m}+b_{n}+2b_{i})=(b_{m}-b_{n})(b_{m}+b_{n}+2b_{j})$

Suy ra $b_{i}=b_{j}$ (mâu thuẫn với lí luận ở trên)

Vậy $n\leq 3$. Có thể chỉ ra ví dụ: $(b_{1},b_{2},b_{3})=(0,2,-4);(c_{1},c_{2},c_{3})=(1,\frac{-1}{2},1)$

Hoàn toàn có thể phủ được.

 

Do bảng khuyết ô trung tâm nên ta chia được bảng thành $4$ hình chữ nhật kích thước $44.45$. Mỗi hình chữ nhật như thế đều phủ được bởi các dải $44 $ đơn vị (dễ chỉ ra).

Nói như Hoàng thì bảng đã cho là $89$x$89$ ?

P/s: Mình cũng làm sai rồi. Cột chính giữa là cột 50... Và cách làm của Hoàng cũng chỉ đúng cho bảng có cạnh là một số chia 8 dư 7 thôi... Ở đây mình cần cách chứng minh bảng có cạnh chia 8 dư 3 không phủ được...

Bài 4:

Đánh thứ tự các cột từ trái sang phải.

Ta điền số vào tất cả các ô của bảng sao cho toàn bộ cột 1 là số 0, toàn bộ cột 2 là số 1, toàn bộ cột 3 là số 0... toàn bộ cột 99 là số 0.

Mỗi viên gạch đều che phủ phần diện tích có tổng các số được ghi trong các ô là chẵn.

Mà tổng các số được điền vào bảng là $49.99$ là số lẻ.

Vậy không thể lát bảng ô vuông như đề bài. 

Câu 5:

Bằng quy nạp theo $n$, ta chứng minh được đẳng thức: $u_{m+n}=u_{m-1}u_{n}+u_{m}u_{n+1}$

Lại dùng quy nạp và sử dụng đẳng thức trên, ta chứng minh được "Nếu $a\vdots b$ thì $u_{a}\vdots u_{b}$". Bài toán chỉ là thế số vào kết quả này.

Bài 2, ngày 2:

Từ giả thiết thì các số nguyên tố $p_2$ và $p_3$ chỉ nhận 2 trong 3 giá trị $\begin{Bmatrix} p_1+2;p_1+4;p_1+6 \end{Bmatrix}$. Nếu chúng cách nhau đúng 2 đơn vị thì ta quay về bài toán đơn giản là tìm 3 số nguyên tố tạo thành cấp số cộng có công sai 2. Còn nếu không thì ta có 4 số nguyên tố đã cho là $p_1;p_2=p_1+2;p_3=p_1+6;p_4=p_1+8$. Lần lượt cho $p_1$ chạy qua hệ thặng dư thu gọn module $30$ thì chỉ có $p_1\equiv 11 (mod 30)$ là thỏa $p_2$, $p_3$ hoặc $p_4$ nguyên tố cùng nhau với 30. Từ đó có thể kết luận.

Nếu có tối đa 3 khoảng cách bằng nhau thì khoảng cách giữa số lớn nhất và số bé nhất sẽ không nhỏ hơn $3(1+2+3+4+5+6)+7=70$. Điều này là mâu thuẫn với giả thiết. 

$P$ là số nguyên thì $x^{2}y+y^{2}x+8x \vdots xy +4\Rightarrow 4x-4y\vdots xy+4$

Đến đây ta có $\left | 4x-4y \right |\geq xy+4$ , dẫn đến 2 trường hợp $(x+4)(4-y)\geq 20$ và $(y+4)(4-x)\geq 20$. Do $x,y$ nguyên dương nên giới hạn được $x,y$. Từ đó thử lại. 

Giải phương trình nghiệm nguyên dương $x^{y}y^{x}=(x+y)^{z}$

Bài 2b, ngày 1

$A= ad+bc\Rightarrow 24A=2(3.4a.d+2.3b.2c)\leq 3(16a^2+d^2)+2(9b^2+4c^2)=30a^2+10(a^2+b^2)+5(a^2+b^2+c^2)+3(a^2+b^2+c^2+d^2)\leq 240\Rightarrow A\leq 10$ (đpcm)

$M$ nằm trong tam giác $ABC$ nhé : )

Cho trước hai số nguyên dương $m$ và $n$. Hãy tìm số nguyên dương $y$ nhỏ nhất sao cho $3^{y}\leq 2^{my-n}$

Từ giả thiết thì $(1-x)(1-z)z\geq 0$ $\Rightarrow z-zx\geq z^2(1-x)\Rightarrow (x+y+z)-(xy+yz+zx)\geq \sum z^2 (1-x)$

Ta cần chứng minh $1\geq x+y+z-(xy+yz+zx)\Leftrightarrow xyz\geq (x-1)(y-1)(z-1)$

Bất đẳng thức này đúng vì vế trái không nhỏ hơn 0, vế trái không lớn hơn 0.

Ta có đpcm

$(x;y;z;n)=(1;1;1;0)$

Nên thêm điều kiện là $x,y,z$ khác $1$ hay là $n$ khác 0 ha. 

Ta đặt $d(x)$ là số các ước dương của số nguyên dương $x$. Tìm số nguyên dương $n$ sao cho:

$d(d_{(n)}).d(d_{(n)}-1)=d(n)$