Vậy điều kiện của $xy$ là gì bạn???

Do x > 0, y > 0 nên theo AM - GM $4xy=x+y\geq 2\sqrt{xy}\Rightarrow 2\sqrt{xy}(2\sqrt{xy}-1)\geq 0\Rightarrow xy\geq \frac{1}{4}$

Vậy $1\geq xy\geq\frac{1}{4}$

Đặt $x=b/a$, $y=c/b$, $z=a/c\Rightarrow xyz=1$. Bđt đã cho trở thành:

$\frac{1}{(1+x)^2}+\frac{1}{(1+y)^2}+\frac{1}{(1+z)^2}\geq \frac{3}{4}$

Bạn có thể tham khảo cách chứng minh bài này ở đây: http://diendantoanho...eft-1a-right-2/

có thể giúp e biến đổi chỗ này không em biến đổi mãi mà không ra

Do x + 1 > 0, y + 1 > 0, $\Rightarrow \frac{x+y}{2}+1>0$. Ta có:
$\frac{x}{x+1}+\frac{y}{y+1}\leq 2\frac{\frac{x+y}{2}}{\frac{x+y}{2}+1}$
$\Leftrightarrow \frac{xy+x+xy+y}{(x+1)(y+1)}\leq \frac{2(x+y)}{x+y+2}$

$\Leftrightarrow (2xy+x+y)(x+y+2)\leq 2(x+y)(xy+x+y+1)$

$\Leftrightarrow 2xy(x+y)+(x+y)^2+4xy+2(x+y)\leq 2xy(x+y)+2(x+y)^2+2(x+y)$

$\Leftrightarrow 4xy\leq (x+y)^2\Leftrightarrow (x-y)^2\geq 0$

Bài 2: Cho $x, y \in \mathbb{R} ; x^2 + y^2 = xy + 3$
Tìm min, Max của $Q = \frac{1}{x^3 + y^3} + \frac{1}{xy}$

$x^2+y^2=xy+3\Leftrightarrow xy=\frac{(x+y)^2-3}{3}$. Thay vào biểu thức Q:
$Q=\frac{1}{(x+y)^3-3xy(x+y)}+\frac{1}{xy}=\frac{1}{3(x+y)}+\frac{3}{(x+y)^2-3}$
 
Đặt $x+y=t$, xét hàm $f(t)=\frac{1}{3t}+\frac{3}{t^2-3}$
Ta có $xy=\frac{(x+y)^2-3}{3}\leq \frac{(x+y)^2}{4}$ với mọi $x\in \mathbb{R}\Rightarrow -2\sqrt{3}\leq x+y\leq 2\sqrt{3}$
Dựa vào bảng biến thiên của f(t) ta thấy f(t) không đạt GTLN và GTNN trên $[-2\sqrt{3},2\sqrt{3}]$
 
Lưu ý: Thực ra phương trình f'(t)=0 có nghiệm khá lẻ xấp xỉ -0.7
 
 

Bài 3: Cho $x, y \in \mathbb{R} ; x^2 + xy + y^2 = 3$
Tìm min, Max của $S = x^3 + y^3 - 3x - 3y$

$x^2+xy+y^2=3\Leftrightarrow xy=\frac{(x+y)^2}{3}$. Thế vào biểu thức S:
$S=(x+y)^3-3xy(x+y)-3(x+y)=-2(x+y)^3+6(x+y)$
 
Đặt $x+y=t$, xét hàm $f(t)=-2t^3+6t$.
Ta có $xy=(x+y)^2-3\leq \frac{(x+y)^2}{4}$ với mọi x, nên $-2\leq x+y\leq 2$
$f'(t)=-6t^2+6=0\Leftrightarrow t=\pm 1$
 
Dựa vào bảng biến thiên của hàm f(t) trên [-2, 2]:
- S đạt GTLN bằng 4, xảy ra khi và chỉ khi t = 1 hoặc t = -2, hay (x, y) = {(-1, -1); (-1, 2); (2, -1)}
- S đạt GTNN bằng -4, xảy ra khi và chỉ khi t = -1 hoặc t = 2, hay (x, y) = {(1, 1); (1, -2); (2, -1)}

Cách giải hình học:

$A=\sqrt{2}\left (\sqrt{x^2+y^2-x+y+\frac{1}{2}}+\sqrt{x^2+y^2+x-y+\frac{1}{2}}+\sqrt{x^2+y^2+2x+2y+2}\right )$

$=\sqrt{2}\left (\sqrt{\left (x-\frac{1}{2}\right )^2+\left (y+\frac{1}{2}\right )^2}+\sqrt{\left (x+\frac{1}{2}\right )^2+\left (y-\frac{1}{2}\right )^2}+\sqrt{(x+1)^2+(y+1)^2}\right )$

 

Trên mặt phẳng tọa độ Oxy, lấy các điểm $A\left (\frac{1}{2},-\frac{1}{2}\right )$, $B\left (-\frac{1}{2},\frac{1}{2}\right )$, C(-1, -1). Ta cần tìm GTNN của $\sqrt{2}(MA+MB+MC)$.

 

Để MA + MB + MC đạt GTNN thì M phải là điểm Fermat (hay điểm Torricelli) của tam giác ABC (mình sẽ không chứng minh, các bạn có thể tham khảo Google hoặc http://en.wikipedia....ki/Fermat_point). Dễ thấy tam giác ABC nhọn nên M sẽ nằm trong tam giác. Cách dựng điểm M như sau:

- Dựng ra phía ngoài tam giác ABC các tam giác đều ABC', CAB'

- Giao điểm của BB' và CC' là điểm M cần tìm.

 

Ta tính được

$C' = \left (\frac{3}{2}, \frac{3}{2}\right )$, phương trình đường thẳng CC': $x-y=0$

$B' = \left (-\frac{1}{4}+\frac{\sqrt{3}}{4}, -\frac{3}{4}-\frac{3\sqrt{3}}{4}\right )$, phương trình đường thẳng BB': $\left (\frac{5}{4}+\frac{3\sqrt{3}}{4}\right )x+\left (\frac{1}{4}+\frac{\sqrt{3}}{4}\right )y+\frac{1}{2}+\frac{\sqrt{3}}{4}=0$

 

Suy ra $M=\left (-\frac{\sqrt{3}}{6},-\frac{\sqrt{3}}{6}\right )$, khi đó biểu thức A đạt GTNN là $2+\sqrt{3}$

1) Xét hàm số $f(x)=4\sqrt{x}-x^2$

$f'(x)=\frac{2}{\sqrt{x}}-2x=0\Leftrightarrow x=1$

Từ bảng biến thiên của hàm số f(x) ta thu được $f(x)\leq 3$ với mọi x>0

Vậy GTLN của A là 9, xảy ra $\Leftrightarrow a=b=c=1$

 

2) $B\leq 2(a^2+b^2+c^2)-4(\sqrt{a}+\sqrt{b}+\sqrt{c})-3(a^2+b^2+c^2)=A$

Vậy GTLN của B là 9, xảy ra $\Leftrightarrow a=b=c=1$

 

3) Theo câu 2:

$C=\frac{ab+bc+ca+2(\sqrt{a}+\sqrt{b}+\sqrt{c})}{a^2+b^2+c^2+3}\leq \frac{9+3(a^2+b^2+c^2)}{2(a^2+b^2+c^2+3)}=\frac{3}{2}$

Vậy GTLN của C là $\frac{3}{2}$, xảy ra $\Leftrightarrow a=b=c=1$.

@solution co the noi ro hon duoc khong?

$a+b+c+\sqrt[3]{abc}\geq 2\sqrt{ab}+2\sqrt{c\sqrt[3]{abc}}\geq 4\sqrt[4]{abc\sqrt[3]{abc}}=4\sqrt[3]{abc}$

 

P/s: Bạn Solution cũng không online từ năm 2005 đến giờ. Mình nghĩ bạn nên lập chủ đề mới để hỏi, không nên gửi bài vào những chủ đề đã cũ.

Phần đặt ẩn x, y ban đầu của bạn rất hay. Cho mình hỏi với dạng bài tập như thế nào thì nên đặt như vậy.

Mình chỉ học tập kinh nghiệm từ bài này: http://diendantoanho...t-bc-right-4c2/. Theo ý kiến cá nhân mình, những bài bđt ba biến, nhưng chỉ đối xứng với hai biến (trong bài của bạn thì đối xứng với b và c) thì có thể sử dụng.

Khả năng là không tồn tại max

Cho $a=b=10^-4, c=10^8$, kết quả xấp xỉ 3333:

http://www.wolframal...2*10^8+10^(-8))

 

Nếu cho $a=b=10^-5, c=10^10$, kết quả xấp xỉ 33333:

http://www.wolframal...*10^10+10^(-5))

$(a+b)(a+c)=4a^2\Rightarrow \left (1+\frac{b}{a}\right )\left (1+\frac{c}{a}\right )=4$

Đặt $x=\frac{b}{a}$, $y=\frac{c}{a}$, ta có $(1+x)(1+y)=4\Leftrightarrow x+y+xy=3$

 

$\Rightarrow P=4\left (\frac{x}{1+x}+\frac{y}{1+y}\right )+2xy-\sqrt{7-3xy}$

$\Rightarrow P=x+y+4xy-\sqrt{7-3xy}=3+3xy-\sqrt{7-3xy}$

 

Đặt $t=xy$. Theo AM-GM $3=x+y+xy\geq xy+2\sqrt{xy}\Rightarrow 1\geq t>0$

 

Xét hàm $f(t)=3+3t-\sqrt{7-3t}$.

Ta có $f'(t)=3+\frac{21}{2\sqrt{7-3t}}>0\Rightarrow $ f(t) đồng biến trong khoảng (0; 1], do đó $f(t)>f(0)=3-7\sqrt{7}$

 

Vậy P không tồn tại GTNN

 

bạn ơi mình chưa hiểu tại sao 

$xyz\geq (x+y-z)(x+z-y)(z+y-x)$

Chứng minh:

- Nếu $x+y-z<0\Rightarrow y+z-x>2y>0$ và $z+x-y>2x>0$

$\Rightarrow xyz>0>(x+y-z)(y+z-x)(z+x-y)$.

Tương tự cho các trường hợp $y+z-x<0$ và $z+x-y<0$

 

- Nếu $x+y-z\geq 0$, $y+z-x\geq 0$ và $z+x-y\geq 0$:

Theo AM-GM $\sqrt{(x+y-z)(y+z-x)}\leq y$

$\sqrt{(y+z-x)(z+x-y)}\leq z$

$\sqrt{(z+x-y)(x+y-z)}\leq x$

Nhân từng vế 3BĐT trên ta được $xyz\geq (x+y-z)(y+z-x)(z+x-y)$

 

- Vậy BĐT đã cho đúng.

 

Nhận xét: Nếu khai triển ra thì đây là bđt Schur với n=1

$a^3+b^3+c^3+3abc\geq a^2(b+c)+b^2(c+a)+c^2(a+b)$

Bài này nằm trong đề thi Olympic Toán Mỹ năm 1980.

 

Giả sử $x\geq y\geq z$. Ta có:

$3\sqrt[3]{(1-y)(1-z)(y+z+1)}\leq (1-y)+(1-z)+(y+z+1)=1$

$\Rightarrow (1-x)(1-y)(1-z)\leq \frac{1-x}{y+z+1}$

$\Rightarrow \frac{x}{y+z+1}+(1-x)(1-y)(1-z)\leq \frac{1}{y+z+1}$ (1)

 

Mặt khác $x\geq y\geq z$

$\Rightarrow \frac{y}{x+z+1}\leq \frac{y}{y+z+1}$ (2)

$\frac{z}{x+y+1}\leq \frac{z}{y+z+1}$ (3)

 

Từ (1), (2), (3)

$\Rightarrow \frac{x}{y+z+1}+\frac{y}{z+x+1}+\frac{z}{x+y+1}+(1-x)(1-y)(1-z)\leq 1$

 

Vậy GTLN của P = 1, xảy ra $\Leftrightarrow (x,y,z)=(1,0,0)$ hoặc $(1,1,0)$ và các hoán vị

1) Trước hết ta chứng minh $\frac{x}{x+1}+\frac{y}{y+1}\leq2\frac{\frac{x+y}{2}}{\frac{x+y}{2}+1}$ với x, y > -1.

Sau khi biến đổi (với x, y > -1), bất đẳng thức trên tương đương với $(x-y)^2\geq0$.

 

Ta có:

$Q=\frac{x}{x+1}+\frac{y}{y+1}+\frac{z}{z+4}$

$\leq2\frac{\frac{x+y}{2}}{\frac{x+y}{2}+1}+\frac{z}{z+4}=\frac{2z}{z-2}+\frac{z}{z+4}$

 

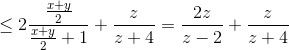
Ta có $x>-1$, $y>-1$ nên $z<2$.

 

Lập bảng biến thiên hàm 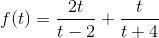 trong khoảng (-4,2), ta tìm được GTLN của Q là $\frac{1}{3}$, xảy ra $\Leftrightarrow x=y=\frac{1}{2}$, $z=-1$

$a^{2}+2b^{2}+2ab+a-5b$

$ = a^2+(2b+1)a+\frac{4b^2+4b+1}{4}+b^2-6b+9-\frac{37}{4}$

$ = \left(a+\frac{2b+1}{2}\right)^2+(b-3)^2-\frac{37}{4} \geq -\frac{37}{4}$

Vậy min $a^{2}+2b^{2}+2ab+a-5b = -\frac{37}{4}$ $\Leftrightarrow$ $a=-\frac{7}{2}$, $b=3$

Nếu bạn đã học khảo sát hàm số thì chỉ cần thay $y=1-x$ sau đó khảo sát vế trái là ra kết quả.

Nếu bạn chưa học khảo sát thì có thể chứng minh hai bđt sau bằng biến đổi tương đương

$3\sqrt{1+2x^2}\geq\frac{6}{\sqrt{11}}\left(x-\frac{1}{3}\right)+\sqrt{11}$

$2\sqrt{40+9y^2}\geq\frac{6}{\sqrt{11}}\left(y-\frac{2}{3}\right)+4\sqrt{11}$

cộng từng vế 2 bđt trên ta có đpcm. Đẳng thức xảy ra khi và chỉ khi $x=\frac{1}{3}$, $y=\frac{2}{3}$

Cho x, y, z > 0, C/m $\dfrac{x}{4x+4y+z}+\dfrac{y}{4y+4z+x}+\dfrac{z}{4z+4x+y}\leq\dfrac{1}{3}$

Ta có;
$\dfrac{x}{4x+4y+z}=x\dfrac{1}{(x+2y)+(x+2y)+(2x+z)}$
$\leq \dfrac{1}{9}x (\dfrac{1}{x+2y}+\dfrac{1}{x+2y}+\dfrac{1}{2x+z})$
<=> $\dfrac{x}{4x+4y+z}\leq\dfrac{1}{9}(\dfrac{2x}{x+2y}+\dfrac{x}{2x+z})$

Tương tự
$\dfrac{y}{4y+4z+x}\leq\dfrac{1}{9}(\dfrac{2y}{y+2z}+\dfrac{y}{2y+x})$
$\dfrac{z}{4z+4x+y}\leq\dfrac{1}{9}(\dfrac{2z}{z+2x}+\dfrac{z}{2z+y})$

Cộng từng vế 3 BĐT trên ta có đpcm. Dấu bằng xảy ra <=> x=y=z

Thế này hả:
Cho a,b,c>0, $ab+bc+ca=1$
$\dfrac{a}{\sqrt{a^2+1}}+\dfrac{b}{\sqrt{b^2+1}}+\dfrac{c}{\sqrt{c^2+1}}$

Ta có $\dfrac{a}{\sqrt{a^2+1}}=\dfrac{a}{\sqrt{a^2+ab+bc+ca}}=\dfrac{a}{\sqrt{(a+b)(a+c)}} \leq \dfrac{1}{2}(\dfrac{a}{a+b}+\dfrac{a}{a+c})$
Cộng từng vế với 2 bddt tương tự nữa ta được $P\leq \dfrac{3}{2}$
Dấu bằng xảy ra <=> $a=b=c=\dfrac{\sqrt{3}}{3}$

Đặt $S=x+y; P=xy$. Ta có
${x}^{2}+{y}^{2}=2$ => ${S}^{2}-2P=2$ <=> $P=\dfrac{{S}^{2}-2}{2}$

Ta luôn có ${S}^{2}\geq 4P$ <=> $2 \geq S \geq -2$
mà $x, y \geq 0$ => $0 \leq S \leq 2$

$A={x}^{3}+{y}^{3}={(x+y)}^{3}-3xy(x+y)=\dfrac{-{S}^{3}}{2}+3S$

Khảo sát hàm số với S nằm trong đoạn $[0;2]$

Còn cách lượng giác hóa nữa, ai gõ nốt dùm cái... )

Nếu bạn giải được rồi thì nên post lời giải lên forum, ok?

Ta có;
$\dfrac{{a}^{2}}{a+bc}=\dfrac{{a}^{3}}{{a}^{2}+abc}=\dfrac{{a}^{3}}{{a}^{2}+ab+bc+ca}=\dfrac{{a}^{3}}{(a+b)(a+c)}$
$\dfrac{{a}^{3}}{(a+b)(a+c)}+\dfrac{a+b}{8}+\dfrac{a+c}{8}\geq\dfrac{3a}{4} (2)$
Cộng từng vế 3 BĐT tương tự với BĐT (2) ta có đpcm.
Dấu bằng xảy ra khi và chỉ khi a=b=c=3

Cách sau đây cũng từ Holder mà ra
Ta có:
$\dfrac{a}{\sqrt{{a}^{2}+8bc}}+\dfrac{a}{\sqrt{{a}^{2}+8bc}}+\dfrac{a({a}^{2}+8bc)}{{(a+b+c)}^{3}} \geq \dfrac{3a}{a+b+c}$
cộng từng vế
cuối cùng ta chỉ phải chứng minh
${a}^{3}+{b}^{3}+{c}^{3}+24abc \leq {(a+b+c)}^{3}$

OK, đề đúng là như vậy

Cho $a, b, c, k, l, m \geq 0, a+b+c = 1$
tìm max của
$\dfrac{ab}{ka+lb+mc}+\dfrac{bc}{kb+lc+ma}+\dfrac{ca}{kc+la+mb}$ theo k, l, m
(Bình thường thì với k, l, m đơn giản (nguyên) ta có thể dùng Cauchy - Schwarz)

Cho $a, b, c \geq 0$
CMR
$2(4{a}^{2}+bc){(b+c)}^{3}+2(4{b}^{2}+ca){(c+a)}^{3}+2(4{c}^{2}+ab){(a+b)}^{3} \leq {(a+b+c)}^{5}$
Nếu bằng PP cổ điển thì càng tốt