Chào mọi người mình muốn có tài liệu chuyên của các trường ở tỉnh thành Hà Nội và Thành phố HCM ai có thì up lên nhé

Bài 198. Cho tam giác $ABC$ nội tiếp đường tròn $(O),H$ là trực tâm của tam giác. Tiếp tuyến tại $A$ của đường tròn cắt $CH$ tại $P,$ kẻ phân giác $AD,PD$ cắt $AB$ tại $K.$ Chứng minh rằng $HK$ vuông góc với $AD.$

Bài 2.

- Viết phương trình đường thẳng $AH$ (có điểm đi qua là $H$ và vectơ pháp tuyến $\overrightarrow{DE}$)

- Tham số hóa được tọa độ điểm $A$ từ phương trình trên.

- Từ đó ta tính được tọa độ điểm của $B$ và $C$

- Tính tích vô hướng của $\overrightarrow{AH}.\overrightarrow{BC}=0$

Suy ra được ẩn, từ đó chú ý tọa độ của $A$ là nguyên. Đến đây xong rồi  

Bài 1.

Tham số hóa tọa độ điểm $G$, gọi $P$ là trung điểm của $BC$ suy ra tọa độ điểm $P$ (theo $G$)

Do tam giác $ABC$ cân tại $A$ từ đó $\overline{PA}.\overrightarrow{PM}=0$ từ đó suy ra tọa độ điểm $P$.

Từ đó viết được phương trình đường thẳng $BC$

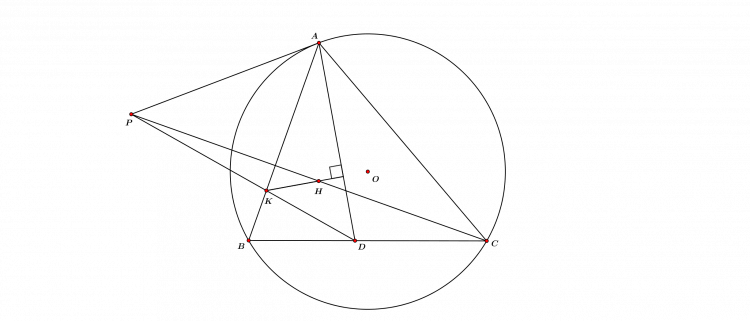
Bài 2.

Gọi $O$ là tâm đường tròn ngoại tiếp của tam giác $ABC$.

Ta dễ dàng viết được phương trình đường thẳng $AH$, tham số hóa điểm $A$, từ đó suy ra tọa độ các điểm $B$, $C$  (theo $A$).

Ta có kết quả $AH//=2OM$ suy ra tọa độ điểm $O$ (theo $A$)

Mà $OD$ vuông góc với $AB$ từ đó suy ra tính tích vô hướng là xong

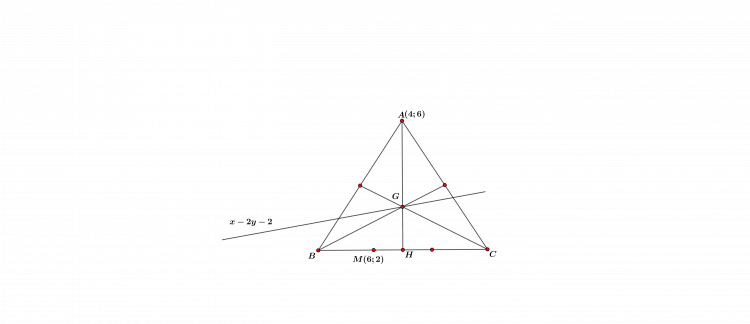
Bài 1. 

Khá dễ dàng, chúng ta có thể thực hiện hướng giải theo các bước sau:

- Tham số hóa tọa độ điểm $G$ từ phương trình $x-2y-2=0$ thành 1 ẩn

- Do $G$ là trọng tâm tam giác $ABC$ nên $AG=2GH$ từ đó tính được tọa độ điểm $H$

- Do $GH$ vuông góc với $BC$ nên $\overrightarrow{HG}.\overrightarrow{HM}=0$. Đến đây ta suy ra được ẩn

- Có tọa độ điểm $G$ rồi, điểm đi qua là $M$ nên viết được phương trình cạnh $BC$

Bài 3.

Đoạn đầu có thể xử lý được bằng trực đẳng phương như sau:

Gọi $W,G$ lần lượt là trung điểm của $BC$, cung $BC$ chứa $A$.

Xét ba đường tròn $(DM)$, $(\varpi )$, $(ADWG)$ thì ta có trục đẳng phương của ba đường tròn đồng quy tại $S$

Do đó dễ chứng minh $SA$ là phân giác ngoài của tam giác ABC tại đỉnh A.

Còn đoạn sau mình xử lý giống bạn dogsteven.

Sử dụng AM-GM : 

(\frac{a}{b}+\frac{b}{c}+\frac{c}{a})^{2}\geq (a+b+c)(\frac{1}{a}+\frac{1}{b}+\frac{1}{c})

Cho các số thực không âm a,b,c thoả mãn $a^{2}+b^{2}+c^{2}=3$.
Chứng minh rằng :
$\frac{a}{a^{2}+2b+3}+\frac{b}{b^{2}+2c+3}+\frac{c}{c^{2}+2a+3}\leq \frac{1}{2}$

ai giải bài này đi

Chuẩn hóa abc=1 thi bdt tương đương với:
$(a+b+c)^2 \geq 4\sum\dfrac{a}{b+c} + 3$
theo BDT co si ta có:
$ 4\sum\dfrac{a}{b+c} \leq \sum \dfrac{a}{2\sqrt{bc}} = \dfrac{1}{2}\sum a\sqrt{a}$
ta sẽ chứng minh :
$(a+b+c)^2 \geq 2\sum a\sqrt{a}+ 3$
Theo BDT cô si:
$\sum \sqrt{a} \geq 3 \Rightarrow 6\sum a\sqrt{a} + 9 \leq 2\sum\sqrt{a}\sum a\sqrt{a} + 3\sum\sqrt{a}$
ta chỉ cần chứng minh:
$(a+b+c)^2 \geq 2\sum\sqrt{a}\sum a\sqrt{a} + 3\sum\sqrt{a}$
$ \Leftrightarrow \sum a(\sqrt{b}-\sqrt{c})^2 + \sum (\sqrt{b}-\sqrt{c})^4 \geq 0 $
BDT  gié

<a href="https://www.fodey.co...atext.asp"><imgsrc="https://r11.fodey.com/2404/e9fdcb5b32d9466dbb18c705777aaf00.1.gif" border=0 width="749" height="117" alt=""></a>

ANH NHÂME SAI ĐIỂM RƠI RỒI ANH ƠI !!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!

C2 :
$2(\dfrac{\dfrac{9}{4}}{a^2 + b^2 + c^2} + \dfrac{1}{2ab} + \dfrac{1}{2bc} + \dfrac{1}{2ac})$ $2(\dfrac{1,5 + 3}{(a + b + c)^2}) = 40,5$

Mặt khác $\dfrac{\dfrac{7}{2}}{a^2 + b^2 + c^2}$ $\dfrac{\dfrac{7}{2}}{\dfrac{1}{3}} = 10,5$

Trừ 2 vế OK

Điểm rơi sai bét kìa 

Xin up lại bài toán hay sau của anh Dragon, bài này thấy anh up mà chưa có giải nên em xin up lại vào topic luôn

Bài toán. Cho a, b, c là các số thực dương thỏa mãn $ab+bc+ca=3abc$. Chứng minh rằng: 

$\sum \frac{1}{\sqrt[3]{a^{3}+bc}}\leq \frac{3}{2}$

Bài 3. (9) VMO 2010 

Cho tam giác $ABC$ nội tiếp $(O)$ cố định $B,C$  và $A$ di chuyển trên $(O)$. Gọi phân giác trong và ngoài của tam giác lần lượt là $AD$ và $AE$ với $D,E$ thuộc $BC$. $M$ là trung điểm của $DE$. $H$ là trực tâm của tam giác $ABC$. Chứng minh rằng đường thẳng qua $H$ vuông góc với $AM$ luôn đi qua một điểm cố định khi $A$ di chuyển trên $(O)$.

Bài 2.

Ta có: $MB.MK=ML.MC$ suy ra $M$ thuộc trục đẳng phương của $(CFL)$ và $(KBE)$.

Do đó $MP$ cũng là trục đẳng phương của hai đường tròn này nên $T$ cũng thuộc đường thẳng đó. 

Do đó $TB.TE=TC.TF$ suy ra $T$ thuộc trục đẳng phương của $(ABE)$ và $(ACF)$ nên giao điểm khác $A$ của hai đường tròn nằm trên $AT$.

Bài 4. (China TST 2002) 

Cho tứ giác lồi $ABCD$, gọi $E, F, P$ lần lượt là giao điểm của $AD$ và $BC$, $AB$ và $CD$,  $AC$ và $BD$. Gọi $O$ là chân đường cao hạ từ $P$ xuống $EF$. Chứng minh rằng $\angle AOD=\angle BOC$ 

Lời giải bài 9  Đây là được coi là $1$ bổ đề cơ bản của đường đối trung. Chứng minh:

Kẻ $GM,GN$ vuông góc với$AB,AC$ thì ta cần chứng minh $\frac{AB}{AC}=\frac{d(G,AB)}{d(G,AC)}=\frac{GM}{GN}$. Mặt khác ta có tam giác $EBG$ đồng dạng tam giác $CFG$ (g.g) nên $2$ đường cao tương ứng có tỉ lệ bằng $\frac{BE}{CF}=\frac{AB}{AC}$. Ta có điều phải chứng minh.

 

Liên quan đến đường đối trung thì mình sẽ đề suất tiếp $1$ bài cũng về đối trung.

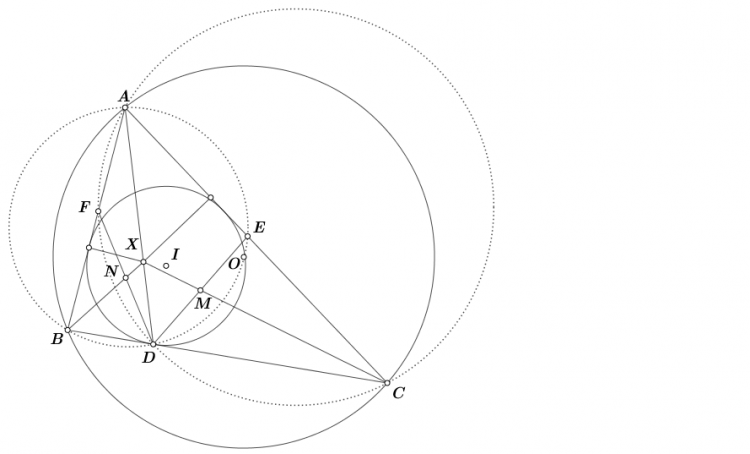
Bài 10. Cho tam giác $ABC$ nội tiếp và ngoại tiếp đường tròn $(O)$ và $(I)$.$(I)$ tiếp xúc $BC$ tại $D$. $(ABD)$ cắt $AC$ tại $E$ và $(ACD)$ cắt $AB$ tại $F$. Gọi $M,N$ lần lượt là trung điểm của $DE,DF$. Chứng minh rằng $OI \perp AD$ khi và chỉ khi $AD,BN,CM$ đồng quy. 

Bài 10. 

Ta có bổ đề quen thuộc sau: $OI$ vuông góc với $AD$ khi và chỉ khi $AD$ là đường đối trung

Ta xét trường hợp thuận: $OI$ vuông góc với $AD$ ta sẽ chứng minh $AD, BN, CM$ đồng quy. Trường hợp còn lại chứng minh tương tự!

Từ bổ đề trên suy ra $AD$ là đường đối trung của tam giác $ABC$ ứng với đỉnh $A$ suy ra $\frac{DB}{DC}=\frac{AB^{2}}{AC^{2}}$

Dễ thấy tam giác $BFD$ ~ tam giác $ECD$ . Suy ra $\frac{BF}{CE}=\frac{DF}{CD}=\frac{DB}{ED}$.

Đến đây dùng định lý Ceva sin là xong 

Không biết cách vẽ hình nên bác thông cảm

P/s: Bài 5 các bác thử áp dung phép nghịch đảo đx qua điểm $A$ sẽ thu đc bài quen thuộc

P/s: Chiều đánh không hoàng ( @Nhoang1608)

Mấy bác đánh cờ tướng ạ     . Bài 11 em có ghi xác định P, Q mà bác !

Bài 5 hơi khó nên mình xin đề xuất một số bài toán mới!

Bài 6. (China TST 2008) Cho tam giác $ABC$ $(AB<AC)$ , đường tròn nội tiếp $(I)$ tiếp xúc với $BC$ tại $D$ . Trên $AD$  lấy điểm $K$ sao cho $CD=CK$ . Giả sử  $AD$ cắt $(I)$  tại điểm thứ hai là $G$ . Gọi $L$ là giao điểm của $GB$  và $CK$ . Chứng minh rằng $K$  là trung điểm của $CL$.

Bài 7. (Trần Minh Ngọc) Cho tam giác $ABC$ nội tiếp $(O)$ . Gọi $P$ là giao điểm của hai tiếp tuyến tại $B$ và $C$  của đường tròn. Trên $AP$ lấy $E, F$ sao cho $BE// AC, CF//AB$. $BE$ cắt $CF$ tại $D$. $CD$, $BD$ tương ứng cắt $(ADE)$, $(ADF)$ tại điểm thứ hai là $M, N$. Chứng minh rằng: $AP$ vuông góc với $MN$.

Bài 3. Trước tiên ta chứng minh bổ đề sau, bổ đề này rất quen thuộc trong những bài toán về đường đối trung.

Bổ đề. Cho tam giác $ABC$ nội tiếp đường tròn tâm $(O)$, $E$ và $F$ lần lượt là các điểm nằm trên $CA, AB$ sao cho $EF//BC$. Đường tròn ngoại tiếp tam giác $ABE$ và tam giác $ACF$ cắt nhau tại $G$ khác $A$. Khi đó $G$ nằm trên đường đối trung xuất phát từ đỉnh $A$.

Chứng minh

Dễ thấy $\bigtriangleup GFB$ đồng dạng với $\bigtriangleup GEC\Leftrightarrow \frac{[GFB]}{[GEC]}=\frac{BF^{2}}{CE^{2}}=\frac{AB^{2}}{AC^{2}}$.

Và ta có: $\frac{[GAB]}{[GAC]}=\frac{[GAB]}{[GFB]}.\frac{[GFB]}{[GEC]}.\frac{[GEC]}{[GAC]}=\frac{BA}{BF}.\frac{CE}{CA}.\frac{AB^{2}}{AC^{2}}=\frac{AB^{2}}{AC^{2}}$.

Suy ra $G$ thuộc đường đối trung ứng với đỉnh $A$.

Quay trở lại bài toán

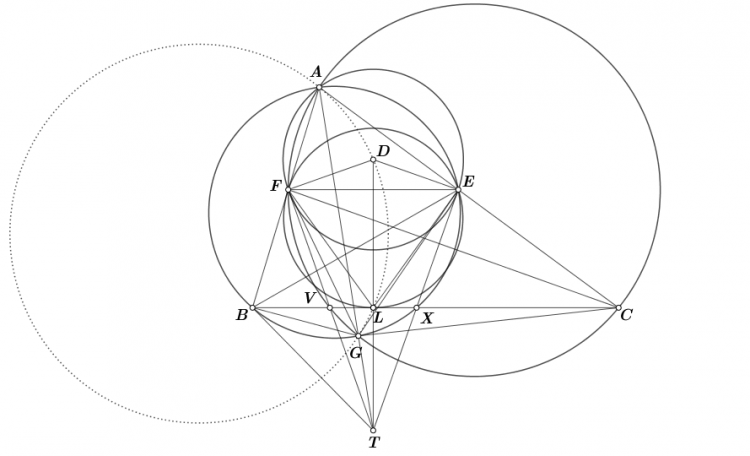
Gọi $T$ là giao điểm của tiếp tuyến tại $E, F$ với đường tròn $(D)$. Theo bổ đề trên kết hợp tính chất quen của tứ giác điều hòa suy ra $A, G, T$ thẳng hàng. Và cũng dễ thấy $T, L, D$ thẳng hàng vì cùng nằm trên trung trực của $EF$.

Gọi $X$ là giao điểm của $TE$ và $BC$ thì ta có: $\widehat{NEC}=\widehat{AFE}=\widehat{ABN}$ suy ra tứ giác $AENB$ nội tiếp.

Mà tứ giác $DENL$ cũng nội tiếp suy ra $TL.TD=TN.TE=TG.TA$ suy ra tứ giác $ADLG$ nội tiếp.

Vậy ta có điều phải chứng minh.

3 bài toán đầu khá đơn giản và đã có ghi nguồn nên ta sẽ xét mở rộng của nó

Nhưng trc hết mik sẽ giải bài sưu tầm trc ( k vẽ hình ):

Bổ đề : Cho $\triangle{ABC}$. Đcao $BE,CF$, trung tuyến $AM$ trc tâm $H$ . $CMR$  $EF,BC$ và đường thẳng qua $H$ vuông góc $AM$ đồng quy

Trở lại bài toán: $MO,NO$ cắt $AC,AB$ tại $Q,P$ suy ra $O$ trc tâm $\triangle APQ$ suy ra $PQ,BC$ đối song trong góc $\angle{BAC}$.

Gọi $AT$ đối trung tg $BAC$ thì $AT$ là trung tuyến $APQ$. Từ đây áp dung bđề cho $\triangle{APQ}$ ta có đpcm

Khi sử dụng bổ đề để chứng minh bài toán bạn có thể chứng minh lại bổ đề đó cho mọi người, vì đấy là điểm mấu chốt của bài toán! ???     

Hy vọng bạn sẽ tham gia Topic nhiều hơn!

em yêu trẩu quá cơ       

Bài 8: Cho $\triangle{ABC}$ tâm nội $I$ . CMR 4 đường thẳng Euler của $BIC,AIB,AIC,ABC$ đồng quy $(Schiffler)$

Bác show lời giải bài 5 được không ạ , tiện thể khi nào giải bác up hình đi kèm với lời giải ạ    như vậy bạn đọc sẽ tiện theo dõi hơn!

Bài mới:

Bài 11. (USA TST 2011) Cho tam giác $ABC$ nhọn có trực tâm $H$ và tâm đường tròn ngoại tiếp là $O$. Gọi $M, N$ lần lượt là trung điểm của $AB, AC$. Các đường thẳng $MH, NH$ cắt $(O)$ tại $P$ và $Q$. Giả sử $MN$ cắt $PQ$ tại $T$. Chứng minh rằng $TA$ là tiếp tuyến của $(O)$.

Bài 12. (Đề chọn HSG Duyên Hải Lớp 11 Chuyên Thái Bình 2013-2014) Cho tam giác $ABC$ vuông tại $A$. Hình chữ nhật $MNPQ$ thay đổi sao cho $M$ thuộc $AB$, N thuộc $AC$, $P, Q$ thuộc $BC$. ${K}=BN\cap MQ, {L}=CM\cap NP, {X}=MP\cap NQ, {Y}=KP\cap LQ$. Chứng minh rằng:

• a) $\widehat{KAB}=\widehat{LAC}$
• b) $XY$ đi qua một điểm cố định.   

Lời nói đầu. Hàng năm mỗi Tỉnh, Thành Phố đều có một đề thi chọn ra những học sinh xuất sắc nhất để ôn tập phục vụ cho kì thi VMO. Với mục đích giúp các bạn có thêm tư liệu cũng như để học hỏi kinh nghiệm của bản thân, mình xin lập ra topic này! 

Yêu cầu:

-Nội dung các bài toán trong topic không giới hạn, miễn là ghi số thứ tự bài toán!

- Lời giải của bài toán phải đi kèm với hình vẽ, và yêu cầu gõ latex!

- Nhớ ghi nguồn cho bài toán, nếu không rõ nguồn có thể ghi '' Sưu tầm'' và nếu lời giải lấy của một ai đó thì nên tôn trọng người nghĩ ra lời giải đó và ghi tên người giải (tất nhiên có thể có những lời giải, ý tưởng trùng nhau)!

-Kiến thức giải toán là không giới hạn, các bạn có thể dùng nhiều phương pháp nhưng mình vẫn mong muốn có một phương pháp thuần túy nhất!

Hy vọng mọi người sẽ phục vụ cho topic này phát triển!

Còn bây giờ mình xin đề xuất một số bài toán sau!

Bài 1. Cho tam giác $ABC$ với các đường đối trung $BE, CF$. Gọi $M, N$ là trung điểm của $BE, CF$. Chứng minh rằng $BN, CM$ và trung trực của $BC$ đồng quy. 

(IMO Shortlish 2006)

Bài 2. Cho tam giác $ABC$ vuông tại $A$ $(AB<AC)$, trên cạnh $BC$ lấy điểm $N$ sao cho $BA=BN$. Gọi $M$ là trung điểm của $AB$, đường tròn đường kính $AB$ cắt $(ANC)$ tại $P$. Đường thẳng qua $B$ vuông góc với $MP$ cắt $PA$ tại $E$ . Đường thẳng qua $P$ song song với $MP$ cắt $PN$ tại $F$. Chứng minh rằng $PC$ đi qua trung điểm của $EF$.

(Trích đề thi HSG TP Hà Nội Vòng 2 năm 2016-2017)

Bài 3. Cho tam giác $ABC$. Gọi $E, F$ lần lượt thuộc $CA, AB$ sao cho $EF$ song song với $BC$. Đường tròn ngoại tiếp tam giác $ABE, ACF$ cắt nhau tại $G$ khác $A$. Gọi $D$ là tâm đường tròn ngoại tiếp tam giác $AEF$. Đường tròn qua $E, F$ tiếp xúc với $BC$ tại $L$. Chứng minh rằng bốn điểm $A, L , G, D$ đồng viên.

(Trần Quang Hùng)

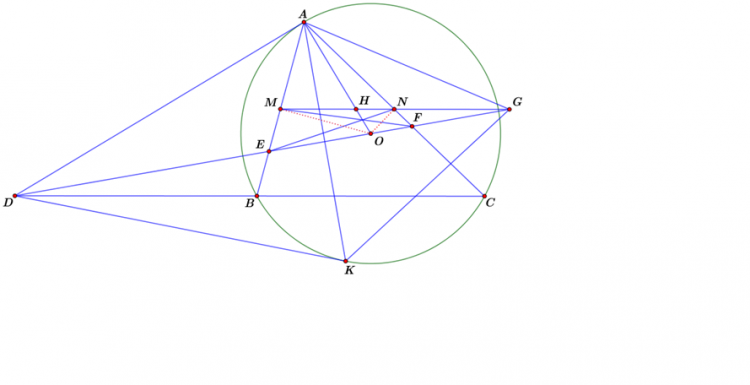
Bài 4. Cho đường tròn $(O)$ ngoại tiếp tam giác $ABC$, tiếp tuyến tại $A$ của đường tròn cắt $BC$ tại $D$. Đường thẳng $DO$ cắt $AB, AC$ tại $E, F$. Gọi $M, N$ lần lượt là trung điểm của $AB, AC$. Chứng minh rằng $EN, FM, AO$ đồng quy.

(Sưu tầm)   

Lời giải bài 8 trong tài liệu của thầy Hùng :http://khoia0.com/Th...-tron-Euler.pdf

xin đề xuất bài tiếp
Bài 9(sưu tầm): Cho $\triangle ABC$ $E,F$ lần lượt thuộc $AB,AC$ sao cho $EF||BC$.$BF\cap CE\equiv D$. Đường tròn $(DBE)\cap (DCF)\equiv G$. Chứng minh $AG$ là đường đối trung.

Bài 9 là đề thi Balkan MO 2009 nhé bạn!

Bài 4. 

Có thể giải bài toán như sau:

Ta tạo dựng mô hình của hàng điểm bằng cách gọi $H$ và $G$ lần lượt là giao điểm của $MN$ với $AO$ và $EF$. Gọi $K$ là tiếp điểm của tiếp

tuyến thứ hai từ $D$ đến $(O)$. Ta có tứ giác  $ABKC$ là tứ giác điều hòa suy ra $A(DKBC)=-1$ . Mà $OM$ vuông góc với $AB$, $ON$ vuông góc

với $AC$, $OH$ vuông góc với $AD$ , $OG$ vuông góc với $AK$ nên theo định lý quen thuộc của hàng điểm suy ra $O(MNHG)=-1$ suy ra

$(MNHG)=-1$  suy ra $A(MNHG)$=-1 suy ra $A(EFOG)=-1$ suy ra $AO, EN,MF$ đồng quy .

Vậy ta có điều phải chứng minh

Bài 13. (Bzasil MO 2017) Cho tam giác $ABC$, trên $AB$ lấy điểm $M$, $AC$ lấy điểm $N$ sao cho $BM=MN=NC$. Tiếp tuyến tại $A$ của đường tròn ngoại tiếp tam giác $ABC$ cắt $MN$ tại $P$. Gọi $I$ là tâm đường tròn nội tiếp tam giác $AMN$. Chứng minh rằng $PA=PI$.

Bài 14. (Sưu tầm) Cho tam giác $ABC$ có ba góc nhọn nội tiếp $(O)$, kẻ ba đường cao $AD, BE, CF$. đồng quy tại $H$. Đường thẳng $EF$ cắt $(O)$ lần lượt tại $M, N$ ($M$ thuộc cung nhỏ AB, $N$ thuộc cung nhỏ $AC$). Gọi $I$ là trung điểm của $BC$, $MI$ cắt $(O)$ tại điểm thứ hai là $K$. Chứng minh rằng $AK$ vuông góc với $HN$.