Để dễ tính toán hơn
Chuyển tập hợp trên về tập hợp {34 số 1, 34 số 2, 34 số 3, 33 số 4, 33 số 5,..., 33 số 59, 33 số 60, 33 số 0}
Tới đây thì mình bí, hehe

$a, b, c \geqslant 0$
$T * 6 = (\frac1{a + 1} + \frac1{b + 1} + \frac1{c + 1})*((a + 1) + (b + 1) + (c + 1)) \geqslant (1 + 1 + 1)^2 = 9$ (Bunhiacopxki)
$\Rightarrow T \geqslant\frac32$
Vậy gtnn của T =$\frac32$, khi a = b = c = 1

Dễ thấy A > 1, B > 4 (*)
Đặt A = $a^2$, B = $b^2$, b, a $\in Z^+$
Có B - A = $b^2 - a^2$ = 3
$(b + a)(b - a) = 3$
$\Rightarrow b + a = 3, b - a = 1$
$\Rightarrow a = 1, b = 2$
$\Rightarrow A = 1, B = 4$, trái với điều kiện (*)
$\Rightarrow$ không tồn tại x, y nguyên dương thỏa mãn bài toán

Bạn nào có thể cho mình một ví dụ về toán dựng hình mà không thể dựng được bằng thước và compa kèm theo chứng minh không dựng được.

Lập số có 5 chữ số khác nhau và khác 0 và 2 thì có $A^5_8$ số
Có 6 vị trí có thể thêm chữ số vào(kí hiệu _) _a_b_c_d_e_
Xét cách đặt 2 chữ số 2
+nếu đặt 2 chữ số 2 cùng 1 chỗ thì có 6 cách
+nếu đặt 2 chữ số 2 vào 2 chỗ khác nhau thì có $C^2_6$ cách
Như vậy có $6 + C^2_6$ cách đặt 2 chữ số 2
Vậy nên số số thỏa mãn đề bài là $A^5_8 * (C^2_6 + 6) = 141120$

Mạn phép đánh giá SKKN của Thế.
Các ví dụ Pascal đều dùng thuật toán vét cạn(duyệt tất cả các trường hợp) nên một số chưa được tối ưu (điển hình ví dụ 3, còn các ví dụ khác phải nghĩ thêm đã... hehe)
Về nguyên tắc thì để chương trình chạy nhanh thì chỗ nào dùng công thức được thì dùng công thức, không được thì mới đếm.

----
Ps: Phần mềm Dcoder giới thiệu bên trên chỉ chạy được khi có mạng.
---
Mạn phép làm lại đề chuyên Nguyễn Du bằng C++ với thuật toán tối ưu hơn bên trên
----------------------
#include <iostream>
using namespace std;

int demDay()
{
int dem = 0;
for (int x1 = 1; x1 < 6; x1++) {
for (int x2 = x1 + 1; x2 <= 6; x2++) {
for (int x3 = 1; x3 < x2; x3++) {
for (int x4 = x3 + 1; x4 <= 6; x4++) {
dem++;
}
}
}
}
return dem;
}

int main(int argc, char *argv[])
{
cout << demDay();
}
//Ket qua 190

Ký hiệu $||x_i||^2_2$ có nghĩa là gì?
Trong đó $x_i$ là một vector

Bài #5 của Ruka,
Chỗ gộp th 2 và 4
Công thức có thể viết lại như sau
$C^3_4.A^2_3 + \frac{C^2_4.A^2_3}{2!}$

Có $C^3_4$ cách chia người thành nhóm 1 và 3
Có $A^2_3$ cách chọn toa cho 2 nhóm vì 1 khác 3, thứ tự khác nhau thì khác nhau
Có $C^2_4$ cách chia 2 nhóm 2 người
Có $\frac{A^2_3}2!$ cách chọn toa nhưng 2 lặp 2 lần nên chia cho 2!

Bạn nghiên cứu ở đây nha: https://en.wikipedia...liptic_integral

Trang đó khó hiểu quá
Các bạn có ai giải được trường hợp cụ thể bên trên không? Còn nữa, nếu f(y) = tích phân hàm trên với cận dưới là hằng số c và cận trên là y thì hàm f trên có thể là elementary function không?

Tính tích phân của hàm $f(x) =\sqrt{ax^4 + bx^3 + cx^2 + dx + e}$
Cận từ $m$ đến $n$ với $0 \le m < n \le 1$

Các bạn cho biết cách tính trường hợp cụ thể cũng được
Tính $\int_0^1\left(\sqrt{x^4 + 2x^3 + 3x^2 +7x + 9}\right)dx$

Đã tìm ra đáp án https://www.google.c...gBiHjqIAB1uXgCu

$n = \left(\overline{a_{t-1}...a_2a_1a_0}\right)_p$
$= a_{t-1}p^{t-1} + ... + a_2t^2 + a_1t + a_0$
Vì n có t chữ số hệ p phân nên $a_{t-1} \geqslant 1, a_i \geqslant 0 \forall i, 0 \leqslant i < t - 1$
$\Rightarrow n \geqslant p^{t-1}$
Lấy $log_p$ 2 vế được
$log_pn \geqslant log_pp^{t-1} = t - 1$ (đpcm)

Không biết đúng hay sai nữa

Dựng các tiếp tuyến chung của hai đường tròn (O ; 2cm) và (O' ; 1cm) biết OO' = 5cm trong các trong các trường hợp sau : a) Tiếp tuyến chung không cắt đoạn thẳng OO'. b) Tiếp tuyến chung cắt đoạn thẳng OO'.

Dễ thấy (O), (O') nằm ngoài nhau
Giả sử tiếp tuyến chung tiếp xúc (O;2) tại A, (O';1) tại B
Hạ BH vuông góc OA tại H
a)+ Phân tích:OH = OA - AH = OA - OB = 2 -1 = 1
+ Cách dựng:
- Dựng đường tròn đường kính OO'
- Dựng đường tròn tâm O bán kính 1 cắt đường tròn trên tại H
- OH cắt (O) tại A
- qua O' dựng đường thẳng // OA cắt (O') tại B nằm cùng phía với A so với OO'
+ Chứng minh: Bạn tự cm
+ Biện luận : Bài toán có 2 nghiệm hình
b)Cách dựng:
- Dựng đ tròn đ kính OO'
- Dựng đ tròn tâm O b kính 2 + 1 = 3 cắt đ tròn trên tại H
- OH cắt (O) tại A
- qua O' dựng đ thẳng // OA cắt (O') tại B khác phía với A so với OO'
+Biện luận : Bài toán có 2 nghiệm hình

Dựng hình chữ nhật $XBX'_1N$ tâm $D$
Dựng hcn $XCX'N$ tâm $E$
Lấy $A'$ đối xứng $A$ qua $M$
$\Rightarrow N$ là tâm nội tiếp $\triangle A'BC$
$\widehat{BA'C} = \widehat{BAC} = \widehat{BAH} + \widehat{CAH} $
$= \widehat{BCH} + \widehat{CBH} = 180^\circ - \widehat{BHC}$
$\Rightarrow A'\in (HBC)$
$X'Y$ cắt $X'_1Z$ tại $F$
$NY \perp PC \Rightarrow Y \in (E, EC)$
$\Rightarrow EK$ là trung trực $XY$
$\Rightarrow EK // X'F$
tương tự, $DK // X'_1F$
$\Rightarrow \widehat{DKE} = \widehat{X'_1FX'} = 180^\circ - \widehat{YXZ}$
+xét $P, A'$ cùng phía với $BC$

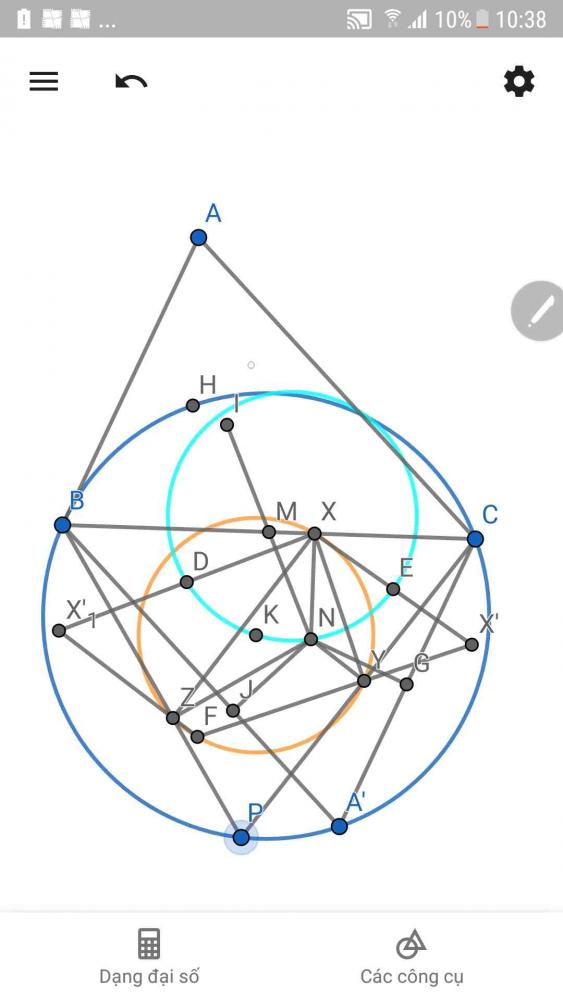
$\widehat{YXZ} = \widehat{YXN} + \widehat{NXZ}$
$= \widehat{YCN} + \widehat{NBZ}$
$= \widehat{A'CN} - \widehat{A'CP} + \widehat{NBA'} + \widehat{A'BP}$
$= \frac12\widehat{B} + \frac12\widehat{C}$
Khi $P \equiv A'$ thì $K \equiv N$ và $\widehat{DKE} = \widehat{DNE} = 180^\circ - \frac12\widehat{B} - \frac13\widehat{C}$
$\Rightarrow K \in (DNE)$ cố định
+xét $P, A'$ khác phía với $CB$


$\widehat{YXZ} = 180^\circ - \widehat{YXC} - \widehat{ZXB}$
$= 180^\circ - \widehat{YGC} - \widehat{ZJB}$
$= 180^\circ - \widehat{ECG} - \widehat{DBJ}$
$= 180^\circ - \frac12\widehat{B} - \frac12\widehat{C} = \widehat{DNE}$
$\Leftrightarrow 180^\circ - \widehat{DKE} = \widehat{DNE}$
$\Rightarrow \widehat{DKE} + \widehat{DNE} = 180^\circ$
$\Rightarrow K \in (DNE)$
đpcm

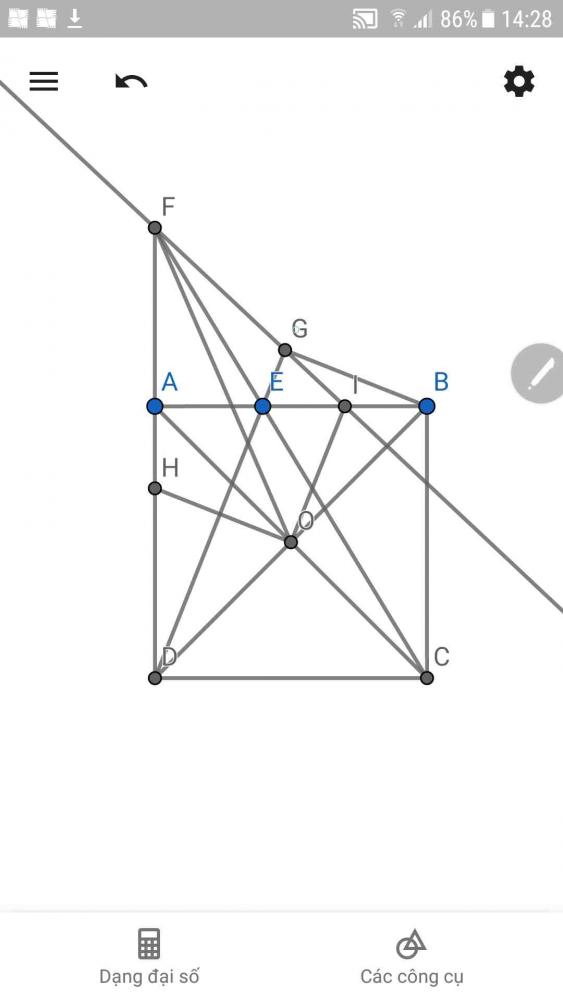
a)
Lấy $J$ trên đoạn $AD$ sao cho $AJ = BI$
$\Rightarrow \triangle OAJ = \triangle OBI$ (c, g, c)
$\Rightarrow OJ = OI$ (1)
Đặt $AE = x, AB = a$
Có $AI = AE + EI = x + \frac12EB = x + \frac12(a - x) = \frac{a + x}2$
Có $\frac{FA}{FD} = \frac{AE}{DC} = \frac xa$
$\Leftrightarrow \frac{FA}{FD - FA} = \frac x{a - x}$
$\Leftrightarrow FA = \frac {ax}{a - x}$
Có $FI^2 = FA^2 + AI^2$
$= \frac{a^2x^2}{(a - x)^2} + \frac{(a + x)^2}4$
$= \frac{4a^2x^2 + (a^2 - x^2)^2}{4(a - x)^2}$
$= \frac{(a^2 + x^2)^2}{4(a - x)^2}$
$\Leftrightarrow FI = \frac{a^2 + x^2}{2(a - x)}$ (2)
Có $FJ = FA + AI = \frac{ax}{a - x} + \frac{a - x}2$
$= \frac{2ax + (a - x)^2}{2(a - x)} = \frac{a^2 + x^2}{2(a - x)}$ (3)
(2, 3) $\Rightarrow FI = FJ$ (4)
(1, 4) $\Rightarrow \triangle OFJ = \triangle OFI$ (c, c, c)
$\Rightarrow \widehat{OFJ} = \widehat{OFI}$
$\Rightarrow O$ cách đều $FD, FI$
$\Rightarrow FI$ luôn tiếp xúc đường tròn nội tiếp $ABCD$
b)
Gọi tia $FI$ là tia $Fx$, cắt $DE$ tại $G$
theo a), $O$ cách đều $BA, Fx$
$\Rightarrow \widehat{OIA} = \widehat{OIx}$
$\Leftrightarrow \widehat{IEG} = \widehat{IGE}$
$\Rightarrow IE = IG = IB$
$\Rightarrow \widehat{DGB} = 90^\circ = \widehat{DAB}$
Vậy, $G$ nằm trên đường tròn ngoại tiếp $ABCD$ (đpcm)

a)
Hạ $HL$ vuông góc $AC$ tại $L$ và cắt $AK$ tại $M$
Đặt $\frac{AB}{AC} = x$
$\frac{AL}{CL} = \frac{AL}{HL}.\frac{HL}{CL} = x^2$
$\Rightarrow \frac{AL}{AC} = \frac{x^2}{x^2 + 1}$
$\Rightarrow \frac{AL}{AN} = \frac{4x^2}{x^2 + 1}$
$AB = AI + BI = IH(\frac1x + x) = xAC$
$\Rightarrow \frac{AC}{IH} = \frac{x^2 + 1}{x^2}$
$\frac{PN}{PH} = \frac{ND}{IH} = \frac{x^2 + 1}{4x^2}$
Áp dụng Menelauyt cho 3 điểm thẳng hàng $A, P, M$ và tam giác $HNL$, có
$\frac{AL}{AN}.\frac{PN}{PH}.\frac{MH}{ML} =1$
$\Rightarrow \frac{MH}{ML} = 1$
Ta có $\triangle BAC\sim\triangle ALH$ {g, g)
$\Rightarrow \frac{BA}{AL} = \frac{AC}{LH} = \frac{2AD}{2LM} = \frac{AD}{LM}$
$\Rightarrow \triangle BAD\sim\triangle ALM$ (c, g, c)
$\Rightarrow \widehat{ABD} = \widehat{LAM} = 90^\circ - \widehat{ADB}$
$\Rightarrow AL\perp BD$(đpcm)

Bổ đề: Cho $\triangle ABC$, $M$ nằm trong tam giác
$AM, BM, CM$ lần lượt cắt $BC, CA, AB$ tại $A_1, B_1, C_1$.
Cm $\frac{MA_1}{AA_1}\overrightarrow{AM} + \frac{MB_1}{BB_1}\overrightarrow{BM} + \frac{MC_1}{CC_1}\overrightarrow{CM} = \overrightarrow{0}$ (1)
Cm:
Kí hiệu $d(A, BC)$ là khoảng cách từ $A$ đến đường thẳng $BC$
ta có $\frac{MA_1}{AA_1} = \frac{d(M, BC)}{d(A, BC)} = \frac {d(M, BC).BC}{d(A, BC).BC} = \frac{S_{MBC}}{S_{ABC}}$
suy ra (1) $\Leftrightarrow \frac{S_{MBC}}{S_{ABC}}\overrightarrow{AM} + \frac{S_{MCA}}{S_{ABC}}\overrightarrow{BM} + \frac{S_{MAB}}{S_{ABC}}\overrightarrow{CM} = \overrightarrow{0}$
$\Leftrightarrow \overrightarrow{AM} + \frac{S_{MCA}}{S_{MBC}}\overrightarrow{BM} + \frac{S_{MAB}}{S_{MBC}}\overrightarrow{CM} = \overrightarrow{0}$
$\Leftrightarrow \overrightarrow{AM} + \frac{MC.d(A, MC)}{MC.d(B, MC)}\overrightarrow{BM} + \frac{MB.d(A, MB)}{MB.d(C, MB)}\overrightarrow{CM} = \overrightarrow{0}$
$\Leftrightarrow \overrightarrow{AM} + \frac{AC_1}{BC_1}\overrightarrow{BM} + \frac{AB_1}{CB_1}\overrightarrow{CM} = \overrightarrow{0}$ (2)
Qua $A$ kẻ đường thẳng // $BM$ cắt $CM$ tại $C_2$
qua $A$ kẻ đ th // $CM$ cắt $BM$ tại $B_2$
(2) $\Leftrightarrow \overrightarrow{AM} + \frac{AC_2}{BM}\overrightarrow{BM} + \frac{AB_2}{CM}\overrightarrow{CM} = \overrightarrow{0}$
$\Leftrightarrow \overrightarrow{AM} + \overrightarrow{C_2A} + \overrightarrow{B_2A} = \overrightarrow{0}$ (3)
vì $AB_2MC_2$ là hình bình hành nên (3) đúng, suy ra (1) đúng (đpcm)

Cm:
$AB', AC', AD'$ lần lượt cắt $CD, DB, BC$ tại $B_2, C_2, D_2$
$AM$ cắt $mp(BCD)$ tại $N$
ta có $B, N, B_2$ thẳng hàng
$\overrightarrow{MB_1} = \frac{B'M}{B'B}\overrightarrow{BN}$ (4)
Áp dụng Menelauyt cho 3 điểm thẳng hàng $A, B', B_2$ và tam giác $BMN$, ta có
$\frac{B'M}{B'B}.\frac{B_2B}{B_2N}.\frac{AN}{AM} = 1$
$\Leftrightarrow \frac{B'M}{B'B} = \frac{AM}{AN}.\frac{B_2N}{B_2B}$ (5)
(4, 5) $\Rightarrow \overrightarrow{MB_1} = \frac{AM}{AN}.\frac{B_2N}{B_2B}.\overrightarrow{BN}$
tương tự với $\overrightarrow{MC_1}, \overrightarrow{MD_1}$
có $\overrightarrow{MB_1} + \overrightarrow{MC_1} + \overrightarrow{MD_1}$
$= \frac{AM}{AN}.(\frac{B_2N}{B_2B}.\overrightarrow{BN} + \frac{C_2N}{C_2C}.\overrightarrow{CN} + \frac{D_2N}{D_2D}.\overrightarrow{DN})$
$= \frac{AM}{AN}.\overrightarrow{0}$ (theo bổ đề)
$= \overrightarrow{0}$
vậy, $M$ là trọng tâm của $\triangle B_1C_1D_1$ (đpcm)

Qua $I$ kẻ đường thẳng vuông góc $OI$ cắt $AB, AC$ lần lượt tại $J, K$ (1)
Có $OIBJ$ nội tiếp $\Rightarrow \widehat{OJI} = \widehat{OBI}$ (2)
$\widehat{OBI} = \widehat{OCI}$ (3)
$OIKC$ nội tiếp $\Rightarrow \widehat{OCI} = \widehat{OKI}$ (4)
(2, 3, 4) $\Rightarrow \widehat{OJI} = \widehat{OKI}$ (5)
(1, 5) $\Rightarrow I$ là trung điểm $JK$ (6)
$\frac{IJ}{HM} = \frac{AI}{AH} = \frac{IK}{HN}$ (7)
(6, 7) $\Rightarrow HM = HN$ (đpcm)

Cho $A$ là ma trận vuông cấp $n$. Chứng minh $det(A) = det(A^T) \quad(*)$

+Với $n = 2$

\[\begin{array}{l}
\det \left( A \right) = {a_{11}}{a_{22}} - {a_{12}}{a_{21}}\\
\det \left( {{A^T}} \right) = {a_{11}}{a_{22}} - {a_{21}}{a_{12}}\\
 \Rightarrow \det \left( A \right) = \det \left( {{A^T}} \right)
\end{array}\]

 

Giả sử (*) đúng với $n = k$ (1). Với $n = k + 1$, ký hiệu $A_{ij}$ là ma trận bù $a_{ij}$. Dễ thấy $(A_{11})^T = (A^T)_{11})$
$$(A_{1j})^T = (A^T)_{j1} \forall 1\leqslant j\leqslant n$$
Khai triển tính $det(A)$ theo hàng 1
\[\det \left( A \right) = \sum\limits_{j = 1}^n {{{\left( { - 1} \right)}^{1 + j}}{a_{1j}}\det \left( {{A_{1j}}} \right)} \quad \left( 2 \right)\]
Khai triển tính $det(A^T)$ theo cột 1
\[\det \left( {{A^T}} \right) = \sum\limits_{j = 1}^n {{{\left( { - 1} \right)}^{1 + j}}{a_{1j}}\det \left( {{{\left( {{A^T}} \right)}_{j1}}} \right)}  = \sum\limits_{j = 1}^n {{{\left( { - 1} \right)}^{1 + j}}} {a_{1j}}\det \left( {{{\left( {{A_{1j}}} \right)}^T}} \right) \quad \left( 3 \right)\]
Từ $(1), (2), (3)$ suy ra (*) đúng với $n = k + 1$
Vậy (*) đúng với mọi $n \geqslant 1$.

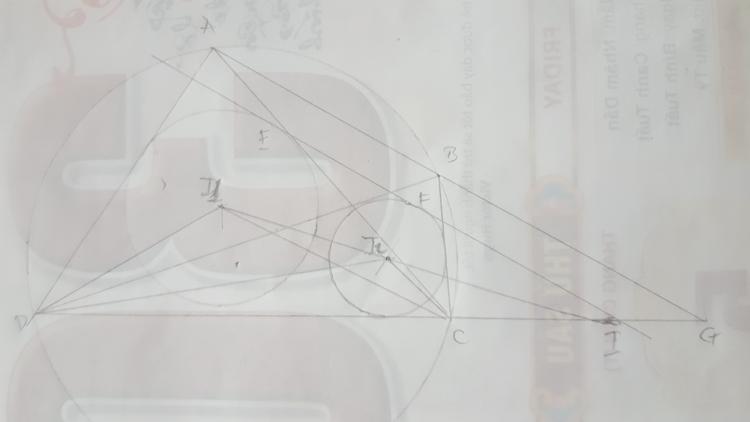
$I_1I_2$ cắt $CD$ tại $I$
Kẻ tiếp tuyến thứ 2 của $(I_1), (I_2)$ tiếp xúc $(I_1), (I_2)$ tại $E, F$
Ta có $E, F, I$ thẳng hàng
$AB$ cắt $CD$ tại $G$
Có $\widehat{I_1CI_2} = \widehat{I_2CD} - \widehat{I_1CD} = \frac12(\widehat{BCD} - \widehat{ACD}) = \frac12\widehat{BCA}$ (1)
Có $\widehat{I_1DI_2} = \widehat{I_1DC} - \widehat{I_2DC} = \frac12(\widehat{ADC} - \widehat{BDC}) =\frac12\widehat{ADB}$ (2)
Có $\widehat{ADB} = \widehat{ACB}$ (3)
(1, 2, 3) $\Rightarrow \widehat{I_1CI_2} = \widehat{I_1DI_2}$
$\Rightarrow I_1I_2CD$ nội tiếp
Ta có $\widehat{AGD} = \widehat{ABD} - \widehat{BDC} = \widehat{ACD} - \widehat{BDC}$ (4)
Có $\widehat{I_1ID} = \widehat{I_1CD} - \widehat{CI_1I_2} = \widehat{I_1CD} - \widehat{I_2DC} = \frac12(\widehat{ACD} - \widehat{BDC})$ (5)
Có $\widehat{EID} = 2\widehat{I_1ID}$ (6)
(4, 5, 6) $\Rightarrow \widehat{EID} = \widehat{AGD}$
$\Rightarrow AB // EI$ (đpcm)

Cho tam giác ABC ngoại tiếp (I) và (I) tiếp xúc BC tại D. Đường thẳng qua D vuông góc AI cắt đường trung bình ứng với đỉnh A của tam giác ABC tại R. J là trung điểm ID. CMR JR vuông góc AD

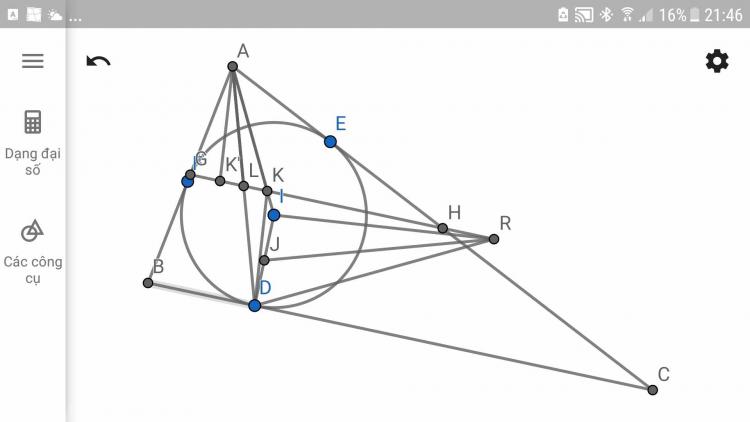
$AI, AD$ lần lượt cắt đường trung bình ứng đỉnh $A$ tại $K, L$
$K'$ đối xứng $K$ qua $L$
$\triangle KDR$ có $KI \perp DR, DI \perp KR$
$\Rightarrow I$ là trực tâm $\triangle KDR$
$\Rightarrow RI \perp KD$ (1)
ta có $L$ là trung điểm $AD, KK'$
$\Rightarrow AKDK'$ là hình bình hành
$\Rightarrow AK' // DK$ (2)
(1, 2) $\Rightarrow AK' \perp RI$ (3)
có $\widehat{K'AK} = \widehat{IRD}$ (góc có cạnh tương ứng vuông góc)
có $\widehat{AK'K} = \widehat{RID}$ (cạnh tương ứng vuông góc)
$\Rightarrow \triangle AK'K \sim \triangle RID$ (g, g) (4)
$\Rightarrow \frac{AK'}{RI} = \frac{K'K}{ID} =\frac{K'L}{IJ}$
$\Rightarrow \triangle AK'L \sim \triangle RIJ$ (c, g, c)
$\Rightarrow \widehat{K'AL} = \widehat{IRJ} $(5)
(3, 5) $\Rightarrow AL \perp JR$ (đpcm)

Bổ đề: Cho 2 tam giác $ABC$ và $A'B'C'$ đồng dạng và cùng hướng
$M, M'$ lần lượt là trung điểm $BC, B'C'$
Cm góc giữa $AM, A'M'$ bằng góc giữa $AB, A'B'$
Cm b đ: Dựng tam giác $AB''C''$ bằng, có cạnh song song với tam giác $A'B'C'$, $M''$ trung điểm $B''C''$
có $\triangle ABC\sim \triangle AB''C''$
$\Rightarrow \frac{AB}{AB''} = \frac{BC}{B''C''} =\frac{BM}{B''M''}$
$\Rightarrow \triangle ABM\sim\triangle AB''M''$ (c, g, c)
$\Rightarrow \triangle ABB''\sim\triangle AMM''$ (c, g, c)
$\Rightarrow \widehat{BAB''} = \widehat{MAM''}$ (đpcm)

Cm:
$MN$ cắt $HK$ tại $J$
$\triangle AED\sim\triangle CFB$
$\Rightarrow \frac{AH}{HD} = \frac{CK}{KB}$
$\Rightarrow \frac{HM}{BD} =\frac{KN}{DB}$
$\Rightarrow HM = KN$
$\Rightarrow MHNK$ là hình bình hành
$\Rightarrow J$ là trung điểm $MN, HK$
Hạ $JI \perp AB$ cắt $EF$ tại $I$
$\Rightarrow I$ trung điểm $PQ$ (1)
Dựng các hình bình hành $JHEX, JKFY$
có $EX = FY$ và $EX // FY$
$\Rightarrow EXFY$ là hình bình hành
$EF$ cắt $XY$ tại $I'$
$\Rightarrow I'$ là trung điểm $EF, XY$
Dựng hình bình hành $ADBU$
$S$ trung điểm $UC$
$V$ trung điểm $AB, DU$
$\Rightarrow A, B, S $ thẳng hàng
Có $\frac{JX}{JY} = \frac{HE}{KF} = \frac{AD}{CB} = \frac{BU}{BC}$
có $\widehat{XJY} = \widehat{UBC}$ (góc có cạnh tương ứng vuông góc)
$\Rightarrow \triangle XJY\sim \triangle UBC$ (c, g, c)
Áp dụng bổ đề, ta có góc giữa $JI', BS$ bằng góc giữa $BU, JX$ bằng 90 độ
$\Rightarrow JI' \perp AB$
$\Rightarrow I \equiv I'$
$\Rightarrow I$ trung điểm $EF, PQ$
$\Rightarrow EP = FQ$ (đpcm)

a)
$(I)$ tiếp xúc $MN, HK$ tại $R, S$
$IR \perp MN, ID \perp HQ, MN // HQ$
$\Rightarrow R, I, D$ thẳng hàng (1)
tương tự $E, I, S$ thẳng hàng(2)
$N$ là giao điểm của 2 tiếp tuyến tại $R, E$ nên $IN$ là phân giác $\widehat{RIE}$ (3)
tương tự $IH$ là phân giác $\widehat{SID}$ )(4)
(1,2,3,4) $\Rightarrow N, I, H $ thẳng hàng (đpcm)
b)
$I$ là trung điểm $ES$
$\Rightarrow \triangle IEN = \triangle ISH$ (g, c, g)
$\Rightarrow NE = SH$ (5)
tương tự $EP = KS$ (6)
(5, 6) $\Rightarrow NP = KH$