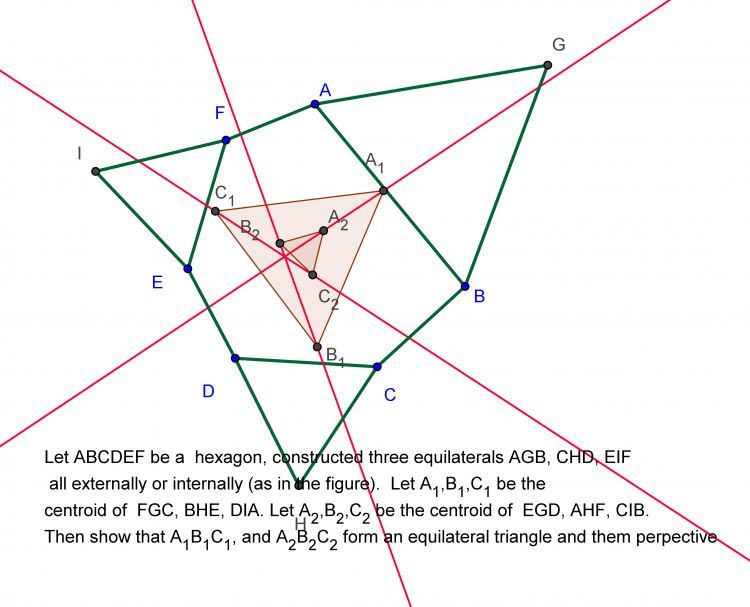
Mở rộng định lý Napoleon liên hệ với đường Kieppert hyperbola.

Cho $ABC$ là một tam giác, $F$ là điểm Fermat(thứ nhất hoặc thứ 2). $K$ là điểm nằm trên đường hyperbol Kiepert, $P$ là điểm nằm trên đường thẳng $FK$. $A_0$ là giao điểm của đường thẳng qua $P$ vuông góc với $BC$ và đường thẳng $AK$, định nghĩa $B_0,C_0$ tương tự. Chứng minh rằng $A_0B_0C_0$ là tam giác đều vị tự của tam giác Napoleon (ngoài hoặc trong)

Một mở rộng rất đẹp của định lý đường thẳng Simson. 

Cho tam giác ABC, và đường thẳng L đi qua tâm đường tròn ngoại tiếp của ABC. Cho một điểm P trên đường tròn ngoại tiếp. Cho đường thẳng AP,BP,CP cắt đường thẳng L tại Ap,Bp,Cp. A0,B0,C0 là chân đường cao của các điểm Ap,Bp,Cp lần lượt lên ba cạnh BC,CA,AB tạo thành các điểm thẳng hàng. Đường thẳng này chia đôi trực tâm và P. Khi P nằm trên đường thẳng L thì đường thẳng A0B0C0 là đường thẳng Simson nổi tiếng.

Hình động: http://tube.geogebra...student/m527653

Định lý Gossard và một phiên bản mở rộng đẹp. 

http://tube.geogebra...student/m645553

 Xét tam giác $ABC$ , đường thẳng $L$ cắt đt Euler của $ABC$ ở $D$ và $L$ cắt $BC$ , $CA$ , $AB$ lần lượt ở $A_0 , B_0 , C_0$ . Gọi $(H_a,O_a) , (H_b,O_b) , (H_c,O_c)$ lần lượt là trực tâm, tâm ngt của $AB_0C_0,BC_0A_0,CA_0B_0$. Gọi $D_a , D_b , D_c$  nằm trên đt Euler  $AB_0C_0,BC_0A_0,CA_0B_0$ thỏa mãn: 

\[ \frac{\overline{D_aH_a}}{\overline{DaOa}}=\frac{\overline{D_bH_b}}{\overline{D_bO_b}}=\frac{\overline{D_cH_c}}{\overline{D_cO_c}} \space=\frac{\overline{DH}}{\overline{DO}}=t  \].

Tam giác $A_1B_1C_1$ tạo bởi 3 đường thẳng qua $D_a,D_b,D_c$ song song $BC , CA , AB$

Chứng minh:

1-$A_1B_1C_1$ vị tự và đối xứng với $ABC$ qua một điểm nằm trên đường thẳng $L$. Khi $t=\infty$  hoặc đường thẳng $L$ trùng với đường thẳng Euler vấn đề này suy biến thành định lý Zeeman-Gossard.

2-Đường thẳng Newton của bốn tứ giác tạo bởi các đường thẳng $(AB,BC,CA,L)$, $(AB,AC,B_1C_1,L)$, $(BC,BA,C_1A_1,L)$ và $(CA,CB,A_1B_1,L)$ cũng đi qua tâm vị tự của hai tam giác $ABC$ và $A_1B_1C_1$

(Phạm Khoa Bằng dịch từ Geogebratube)

Mở rộng định lý Napoleon kết hợp với một lục giác:

Cho $ABCDEF$ là một lục giác bất kỳ, dựng ba tam giác đều $AGB$, $CHD$, $EIF$ cùng ra ngoài hoặc cùng vào trong(hình vẽ đính kèm là dựng ra ngoài). Ta gọi $A_1,B_1,C_1$ lần lượt là trọng tâm của các tam giác $FGC, BHE, DIA$ và $A_2,B_2,C_2$ lần lượt là trọng tâm của các tam giác $EGD, AHF, CIB$. Khi đó hai tam giác $A_1B_1C_1$ và $A_2B_2C_2$ là các tam giác đều và chúng thấu xạ.

Thấy có bài báo này trên trang web của trường đại học Princeton, mọi người cho ý kiến nhé

http://www.princeton.edu/~aloo/fermat

Chứng minh định lý Simson mở rộng của hai tác giả Nguyễn Lê Phước và Nguyễn Chương Chí

 Chung_minh_dinh_ly_mo_rong_duong_thang_Sim_Son.pdf   429.42K   711 Số lần tải

Dao Thanh Oai, A family of Napoleon triangles associated with the Kiepert configuration, The Mathematical Gazette, Published online: 13 March 2015

http://journals.camb...d=0&issueId=544

 TamgiaNapoleon.pdf   309.59K   478 Số lần tải

Liên quan đến định lý lá cờ Anh viết cùng thầy Nguyễn Minh Hà

 La co nuoc Anh.pdf   356.99K   1265 Số lần tải

Dao Thanh Oai, Equilateral triangles and Kiepert perspectors in complex numbers, 105--114.

 FG201509.pdf   94.99K   453 Số lần tải

Giả thuyết trên được chúng tôi phát triển từ bất đẳng thức quen thuộc trong hình học tam giác:

$\sin A.\sin B. \sin C \leq 3.\sqrt{3}/8$

Với không gian hai chiều $f(n,m)=\frac{n}{m}=\frac{n}{2}$ 

Mở rộng đường tròn Lester với đường Neuberg cubic.

Đường Neuberg cubic: Cho tam giác $ABC$, một điểm $P$ là điểm trên đường Neuberg cubic của  $ABC$ nếu thỏa mãn với $P_a,P_b,P_c$ là ba điểm đối xứng của $P$ qua ba cạnh $BC,CA,AB$ thì $AP_a, BP_b, CP_c$ sẽ đồng quy tại một điểm, ta gọi điểm này là $Q$. 

Mở rộng định lý đường tròn Lester: Bốn điểm gồm 2 điểm Fermat, P, Q được định nghĩa như trên nằm trên một đường tròn.

Hình vẽ của mở rộng định lý Lester(#20).

Ký hiệu trong hình vẽ. $X_4$ là trực tâm, $X_{3}$ là tâm ngoại tiếp, $X_{13}$, $X_{14}$ là hai điểm Fermats

Vấn đề của một lục giác lồi nội tiếp và sáu đường tròn Thebault.

Cho lục giác $ABCDEF$ lồi nội tiếp đường tròn $(O)$. Gọi $A_1,B_1,C_1,D_1,E_1,F_1$ lần lượt là các tiếp điểm chung của sáu đường tròn Thebault $(FA,BC,(O))$, $(AB,CD,(O))$, $(BC,DE,(O))$, $(CD,EF,(O))$, $(DE,FA,(O))$, $(EF,AB,(O))$ với $(O)$. Hãy chứng minh $A_1D_1, B_1E_1, C_1F_1$ đồng quy.

http://tube.geogebra.org/m/1352263

Vấn đề mở rộng định lý Feuerbach–Luchterhand

Vấn đề được nêu trong file đính kèm

 June-14-2014-Feuerbach-Luchterhand.pdf   106.14K   541 Số lần tải

Cách xác định $A_1$ còn mờ ám. Vì có hai vị trí $A_1$ (vị trí còn lại nằm ở cung đối diện). Tương tự với $B_1,C_1,...$

Thực ra anh cũng nhận ra điều đó(nhưng lười viết), cảm ơn em nhé. Anh bổ sung như sau:

Nếu đường tròn $A_1$ như hình vẽ thì tất cả các đường tròn Thebault tương ứng với $B_1,C_1,...,F_1$ còn lại như hình vẽ.
Nếu đường tròn tương ứng với $A_1$ phía đối diện thì tất cả các đường trờn tương ứng với $B_1,C_1,...,F_1$ cũng nằm ở phía đối diện
Nếu đường tròn tương ứng với $A_1$ nằm ngoài thì tất cả các đường tròn tương ứng $B_1,C_1,...,F_1$ cũng năm phía ngoài.(nằm ngoài cũng có hai trường hợp)

 

Lời giải cho vấn đề tám đường tròn, Proposed by Đào Thanh Oai, solution by Luis Gonzalez

Bạn Quang Dương có hỏi tôi về việc chứng minh phương trình sau có nghiệm trong khoảng $(-\pi,\pi)$.

$\cos 2x+\cos x.(2-\cos  a-\cos b)+\sin x.(\sin a+\sin b)+1-\cos a-\cos b=0$, trong đó $x$ là ẩn và $a,b$ là tham số.

Theo tôi thì cách làm thông thường như biết đổi lượng giác, quy về phương trình đa thức.... có thể sẽ bế tắc.

1. Quan sát:
 

Cho hai hàm số liên tục $f(x)$ và $g(x)$ với $x \in [a,b]$, khi đó khả năng tồn tại một giá trị $x_0$ thực để $f(x_0)=g(x_0)$ là cao hơn so với khả năng tồn tại giá trị nguyên $y_0$ để $f(y_0)=g(y_0)$. Điều này dễ dàng hình dung qua đồ thị về giao điểm của hai hàm số liên tục và giao điểm của hai hàm số rời rạc. Đối với một đa thức khi bậc của đa thức cao lên thì độ rời rạc của đa thức $f(x)$ ($x$ nguyên) càng cao và dẫn đến giá trị $f(x)+f(y)=f(z)$ với $x,y,z$ nguyên càng trở lên khó khăn. Theo chiều hướng đó khi bậc của đa thức $k$ tăng đến một mức độ nào đó thì sẽ dẫn đến phương trình $f(x)+f(y)=f(z)$ hoàn toàn trở lên vô nghiệm. Xuất phát từ nguyên lý đó tôi đưa ra một giả thuyết như sau(chú ý giả thuyết sau chỉ là một cách để cố gắng thể hiện kết quả trong quan sát trên):

2. Giả thuyết: Cho $a$ là một số nguyên khác $0$, $m,n$ là hai số nguyên dương khác nhau, $g(x)$ là một đa thức bất kỳ cho trước, đặt $f(x)=g(x)+ax^k$, khi đó tồn tại một hằng số nguyên dương $k_0$ để với mọi $k \geq k_0$ thì phương trình:
$$f(x_1)+f(x_2)+....+f(x_n)=f(y_1)+....+f(y_m)$$
không có nghiệm nguyên dương khác một.

Chú ý: Tôi thêm chữ khác 1 vào để loại bỏ trường hợp tầm thường cho phù hợp với ý tưởng xuất phát là độ rời rạc của đa thức tăng lên khi bậc của đa thức tăng lên vì với x=1 thì f(1) không thay đổi khi ta chỉ thay đổi bậc của đa thức. Ngoài ra phản biện tại #2 của Zaraki là cho phiên bản version 1

 

Giả thuyết của anh không đúng, thử với $95800^4+217519^4+414560^4=422481^4$ (R. Frye 1988).

Thực ra, năm 1967, L. J. Lander, T. R. Parkin, and John Selfridge đã đưa ra một giả thuyết, mở rộng cho định lý Fermat lớn:

 

Nếu $k>3$ và $\sum_{i=1}^{n}a_i^k= \sum_{i=1}^mb_j^k$ trong đó $a_i \ne b_j$ với mọi thì $1 \le i \le n, 1 \le j \le m$ có nghiệm nguyên dương thì $m+n \ge k$.

 

Anh có thể xem thêm tại Euler's sum of powers conjecture.

 

Giả thuyết của anh chắc có thể đúng nếu chỉnh điều kiện từ $k \ge m+n$ thành $k>m+n$.

Cảm ơn em. Giáo sư Đào Hải Long cũng cho anh biết thông tin trên, và đưa đường link :

https://en.wikipedia...idge_conjecture

Phiên bản cuối cùng của giả thuyết

Mở rộng định lý Sondat:

Cho tam giác $ABC$, cho $P$ là một điểm bất kỳ trên mặt phẳng, cho đường thẳng $d$ cắt ba cạnh tam giác tại $A_0$, $B_0$, $C_0$ ba đường thẳng tương ứng qua $A_0,B_0,C_0$ và song song với $AP, BP, CP$ tạo thành tam giác $A_1,B_1,C_1$. Theo định lý Maxwell thì ba đường thẳng qua $A_1, B_1, C_1$ và song song với $BC,CA,AB$ một cách tương ứng lại sẽ đồng quy tại một điểm ta gọi điểm này là $P_1$. Khi đó đường thẳng $d$ chi đôi đoạn thẳng $PP_1$. Trong trường hợp $P$ là trực tâm vấn đề này là định lý Sondat.

http://tube.geogebra.org/m/1467027

https://groups.yahoo...s/messages/2673