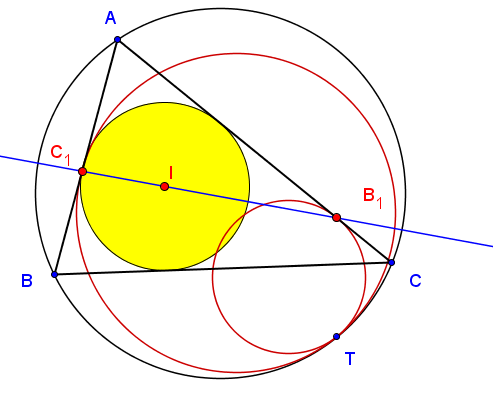
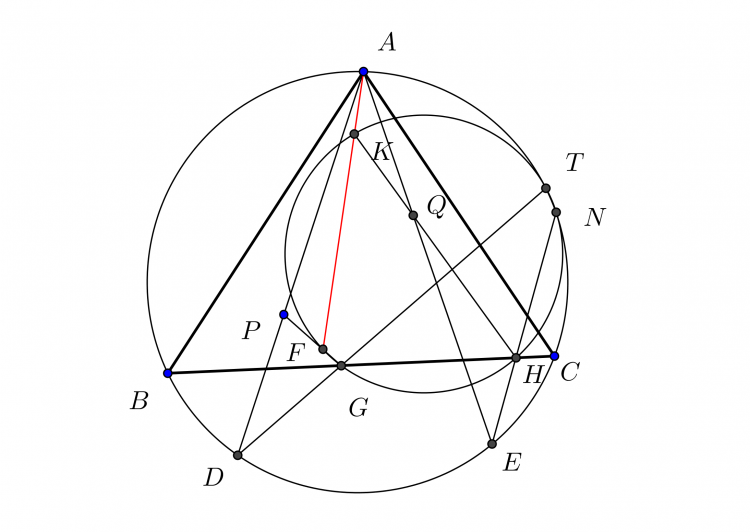
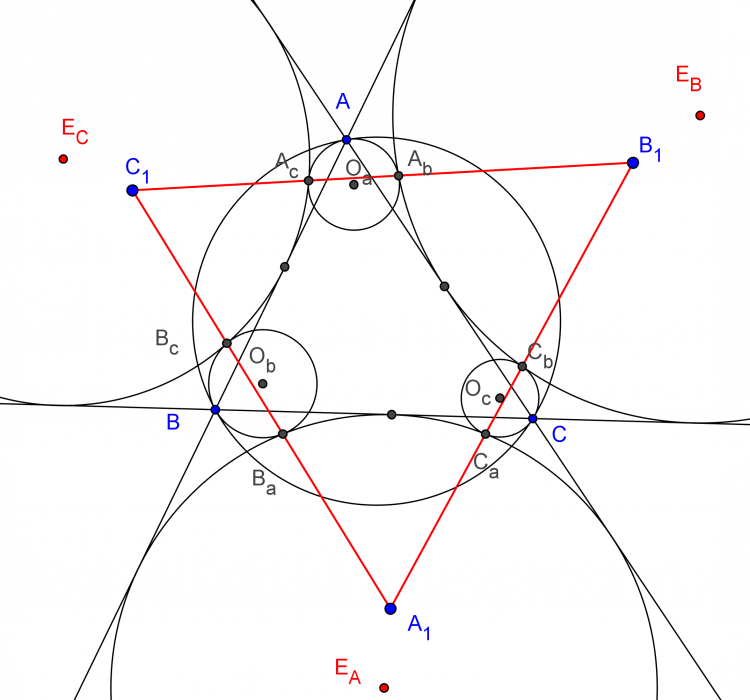
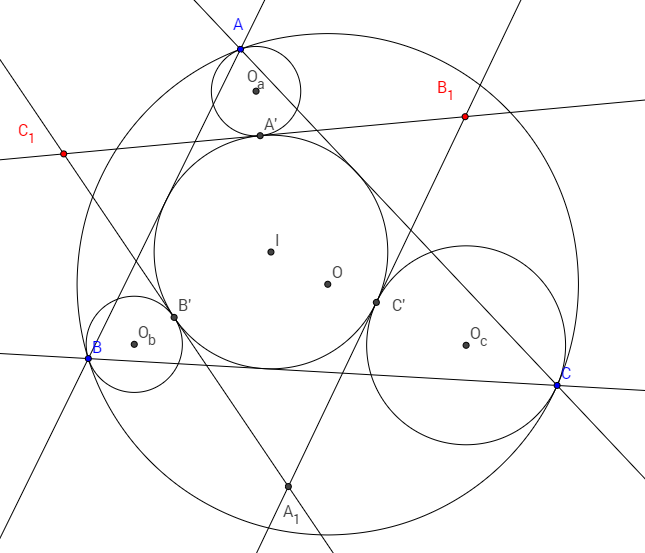
Cho tam giác $ABC$, cho hai đường tròn cùng tiếp xúc với đường tròn ngoại tiếp tại $T$, đường tròn thứ nhất tiếp xúc với $AB$ tại $C_1$, đường tròn thứ hai tiếp xúc với $AC$ tại $B_1$. Chứng minh $B_1, C_1$ và tâm đường tròn nội tiếp tam giác $ABC$ thẳng hàng. Khi hai đường tròn này trùng nhau ta có định lý Nixon [1].

[1] R. C. J. Nixon, Question 10693, Reprints of Educational Times, London (1863-1918) 55 (1891) 107.

cho sáu điểm $A_1, A_2, B_1, B_2, C_1, C_2$ nằm trên một đường tròn tâm $O_1$. Cho đường tròn tâm $O_2$. Dựng hai đường tròn qua $A_1, A_2$ tiếp xúc với $O_2$ tại $A, A'$. Định nghĩa tương tự ta có $B, B'$ và $C, C'$ chứng minh $AA', BB', CC'$ đồng quy.

Mở rộng định lý Lester, định lý Parry, định lý Zeeman-Gossard

Một giả thuyết giống định lý Cayley–Bacharach

Giả thuyết 1: Cho sáu điểm $A, A', B, B', C, C'$ cùng nằm trên một đường bậc hai và đường bậc ba (nào đó). Cho một đường bậc hai đi qua $B, B', C, C'$ và cắt đường bậc ba đó tại $A_1, A_2$. Đường bậc hai đi qua $C, C', A, A'$ và cắt đường bậc ba đó tại $B_1, B_2$. Đường bậc ba đi qua $A, A', B, B'$ và cắt đường bậc ba tại $C_1, C_2$. Khi đó sáu điểm $A_1,A_2, B_1, B_2, C_1, C_2$ nằm trên một đường bậc hai. Nếu ta chọn trước các điểm $A_1, B_1, C_1$ thẳng hàng thì các điểm $A_2, B_2, C_2$ cũng phải thẳng hàng.

Giả thuyết 2: Cho một đường conic cắt một đường bậc ba tại 6 điểm $A, B, C, D, E, F$. Cho một đường conic khác đi qua ba điểm $A,B,C$ cắt đường bậc ba tại $G, H, I$, cho đường conic khác đi qua ba điểm $D, E, F$ cắt đường bậc ba tại $J, Q, K$. Khi đó sáu điểm $G, H, I, J, Q, K$ sẽ nằm trên một đường conic.

Chứng minh giả thuyết 2:
Đây là cách chứng minh cho giả thuyết 2 của một giáo sư (mà mình không hiểu) nhưng cứ trình bày lại ra đây để mọi người tham khảo: 

Áp dụng luật nhóm, nếu như một đường bậc hai giao với một đường bậc ba tại sáu điểm thì tổng sáu điểm phải bằng không. Ta có A+B+C+D+E+F=0; A+B+C+G+H+I=0; D+E+F+J+Q+K=0 => G+H+I+J+Q+K=0 => Sáu điểm G, H, I, J, Q, K nằm trên một đường conic. Giả thuyết mạnh hơn được chứng minh.

Giả thuyết tổng quát: Cho hai đường cong (đa thức) cắt nhau tại $\frac{d^2+3d}{2}+\frac{l^2+3l}{2}+2$ điểm. Nếu $\frac{d^2+3d}{2}+1$ điểm nằm trên đường cong bậc $d$ thì $\frac{l^2+3l}{2}+1$ điểm còn lại sẽ nằm trên đường cong bậc $l$

Vấn đề: Dual của định lý Đào về sáu tâm đường tròn ngoại tiếp (đây là đường tròn nội tiếp).

Cho một lục giác nội tiếp, khi đó đường thẳng nối tâm các đường tròn nội tiếp các tam giác tạo bởi hai cạnh và chung đường chéo chính sẽ đồng quy.

http://tube.geogebra.org/m/1488371

 Giang Nguyen Ngoc's paper.pdf   499.52K   391 Số lần tải

Vấn đề 10 đường tròn:

 Ten circles problem.pdf   29.82K   372 Số lần tải

 Another+then+circles+problem.pdf   54.19K   208 Số lần tải
 

Một số vấn đề về đường tròn Apollonian

Một mở rộng bổ đề Sawayama Lemma và định lý Sawayama-Thebault

 Mot mo rong bo de sawayama Lemma va dinh ly Sawayama Thebault.pdf   129.45K   430 Số lần tải

Mở rộng bổ đề Sawayama

Cho tam giác $ABC$, $P$, $Q$ là hai điểm đẳng giác của nhau. $AP$, $AQ$ cắt đường tròn ngoại tiếp lần lượt tại $D, E$. Hai đường thẳng bất kỳ qua $D, E$ cắt đường tròn ngoại tiếp lần lượt tại hai điểm $T, N$ và cắt đường thẳng BC tại hai điểm $G, H$. Gọi $PG, HQ$ cắt đường tròn $(GHNT)$ tại $K, F$. Khi đó $K, F, A$ thẳng hàng.

Định nghĩa đường tròn $O_a$ là đường tròn tiếp xúc với đường tròn bàng tiếp $(E_b), (E_c)$ và đường tròn ngoại tiếp lần lượt tại $A_b, A_c$ và $A$. Xác định $B_c, B_a, C_a, C_b$ tương tự. Khi đó tam giác tạo bởi ba đường thẳng $A_bA_c, B_cB_a, C_aC_b$ là một tam giác perpective với rất nhiều tam giác:

1-$A_1B_1C_1$ thấu xạ với tam giác ABC

2-$A_1B_1C_1$ thấu xạ với tam giác excentral

3-$A_1B_1C_1$ thấu xạ với tam giác Cevian của điểm Nagel

4-$A_1B_1C_1$ thấu xạ với tam giác cevian  của điêm tâm đường tròn nội tiếp

5-$A_1B_1C_1$ thấu xạ với tam giác Feuerbach

6-$A_1B_1C_1$ thấu xạ với tam giác Extangents

7-$A_1B_1C_1$ thấu xạ với tam giác Apollonius

Phần trên tôi xây dựng tam giác $ABC$ với đường tròn bàng tiếp, tại đây tôi dựng với đường tròn nội tiếp kết quả tương tự.

Dựng đường tròn $O_a$ tiếp xúc với đường tròn ngoại tiếp tại $A$ và đường tròn nội tiếp tại $A'$. Định nghĩa $B', C'$ tương tự. Tiếp tuyến của đường tròn nội tiếp tại ABC tạo ra tam giác $A_1B_1C_1$

1- $A_1B_1C_1$ thấu xạ với tam giác ABC
2- $A_1B_1C_1$ thấu xạ với tam giác excentral 
3- $A_1B_1C_1$ thấu xạ với tam giác Cevian của điểm Gergonne (điểm thấu xạ trùng với 2-)
4- $A_1B_1C_1$ thấu xạ với tam giác cevian của điêm tâm đường tròn nội tiếp
5- $A_1B_1C_1$ thấu xạ với tam giác Feuerbach 
6- $A_1B_1C_1$ thấu xạ với tam giác Extangent 
7- $A_1B_1C_1$ thấu xạ với tam giác Apollonius

Dual của định lý Maxwell.

Cho tam giác $ABC$, và đường thẳng $L$. Đường thẳng $L$ cắt ba cạnh $BC, CA, AB$ tại $A_1, B_1, C_1$. Gọi $A'B'C'$ la tam giác trong mặt phẳng đó sao cho $B'C', C'A', A'B'$ là song song với $AA_1, BB_1, CC_1$. Chứng minh rằng ba đường thẳng đi qua  $A', B', C'$ và lần lượt song song với $BC,CA,AB$ sẽ cắt ba cạnh $B'C', C'A', A'B'$ tại ba điểm thẳng hàng.

Mở rộng định lý Sondat:

Cho tam giác $ABC$, cho $P$ là một điểm bất kỳ trên mặt phẳng, cho đường thẳng $d$ cắt ba cạnh tam giác tại $A_0$, $B_0$, $C_0$ ba đường thẳng tương ứng qua $A_0,B_0,C_0$ và song song với $AP, BP, CP$ tạo thành tam giác $A_1,B_1,C_1$. Theo định lý Maxwell thì ba đường thẳng qua $A_1, B_1, C_1$ và song song với $BC,CA,AB$ một cách tương ứng lại sẽ đồng quy tại một điểm ta gọi điểm này là $P_1$. Khi đó đường thẳng $d$ chi đôi đoạn thẳng $PP_1$. Trong trường hợp $P$ là trực tâm vấn đề này là định lý Sondat.

http://tube.geogebra.org/m/1467027

https://groups.yahoo...s/messages/2673

Mở rộng định lý Napoleon kết hợp với một lục giác:

Cho $ABCDEF$ là một lục giác bất kỳ, dựng ba tam giác đều $AGB$, $CHD$, $EIF$ cùng ra ngoài hoặc cùng vào trong(hình vẽ đính kèm là dựng ra ngoài). Ta gọi $A_1,B_1,C_1$ lần lượt là trọng tâm của các tam giác $FGC, BHE, DIA$ và $A_2,B_2,C_2$ lần lượt là trọng tâm của các tam giác $EGD, AHF, CIB$. Khi đó hai tam giác $A_1B_1C_1$ và $A_2B_2C_2$ là các tam giác đều và chúng thấu xạ.

Liên quan đến định lý lá cờ Anh viết cùng thầy Nguyễn Minh Hà

 La co nuoc Anh.pdf   356.99K   1265 Số lần tải

Định lý Gossard và một phiên bản mở rộng đẹp. 

http://tube.geogebra...student/m645553

 Xét tam giác $ABC$ , đường thẳng $L$ cắt đt Euler của $ABC$ ở $D$ và $L$ cắt $BC$ , $CA$ , $AB$ lần lượt ở $A_0 , B_0 , C_0$ . Gọi $(H_a,O_a) , (H_b,O_b) , (H_c,O_c)$ lần lượt là trực tâm, tâm ngt của $AB_0C_0,BC_0A_0,CA_0B_0$. Gọi $D_a , D_b , D_c$  nằm trên đt Euler  $AB_0C_0,BC_0A_0,CA_0B_0$ thỏa mãn: 

\[ \frac{\overline{D_aH_a}}{\overline{DaOa}}=\frac{\overline{D_bH_b}}{\overline{D_bO_b}}=\frac{\overline{D_cH_c}}{\overline{D_cO_c}} \space=\frac{\overline{DH}}{\overline{DO}}=t  \].

Tam giác $A_1B_1C_1$ tạo bởi 3 đường thẳng qua $D_a,D_b,D_c$ song song $BC , CA , AB$

Chứng minh:

1-$A_1B_1C_1$ vị tự và đối xứng với $ABC$ qua một điểm nằm trên đường thẳng $L$. Khi $t=\infty$  hoặc đường thẳng $L$ trùng với đường thẳng Euler vấn đề này suy biến thành định lý Zeeman-Gossard.

2-Đường thẳng Newton của bốn tứ giác tạo bởi các đường thẳng $(AB,BC,CA,L)$, $(AB,AC,B_1C_1,L)$, $(BC,BA,C_1A_1,L)$ và $(CA,CB,A_1B_1,L)$ cũng đi qua tâm vị tự của hai tam giác $ABC$ và $A_1B_1C_1$

(Phạm Khoa Bằng dịch từ Geogebratube)

Một mở rộng rất đẹp của định lý đường thẳng Simson. 

Cho tam giác ABC, và đường thẳng L đi qua tâm đường tròn ngoại tiếp của ABC. Cho một điểm P trên đường tròn ngoại tiếp. Cho đường thẳng AP,BP,CP cắt đường thẳng L tại Ap,Bp,Cp. A0,B0,C0 là chân đường cao của các điểm Ap,Bp,Cp lần lượt lên ba cạnh BC,CA,AB tạo thành các điểm thẳng hàng. Đường thẳng này chia đôi trực tâm và P. Khi P nằm trên đường thẳng L thì đường thẳng A0B0C0 là đường thẳng Simson nổi tiếng.

Hình động: http://tube.geogebra...student/m527653

Dao Thanh Oai, Equilateral triangles and Kiepert perspectors in complex numbers, 105--114.

 FG201509.pdf   94.99K   453 Số lần tải

Mở rộng đường tròn Lester với đường Neuberg cubic.

Đường Neuberg cubic: Cho tam giác $ABC$, một điểm $P$ là điểm trên đường Neuberg cubic của  $ABC$ nếu thỏa mãn với $P_a,P_b,P_c$ là ba điểm đối xứng của $P$ qua ba cạnh $BC,CA,AB$ thì $AP_a, BP_b, CP_c$ sẽ đồng quy tại một điểm, ta gọi điểm này là $Q$. 

Mở rộng định lý đường tròn Lester: Bốn điểm gồm 2 điểm Fermat, P, Q được định nghĩa như trên nằm trên một đường tròn.

Vấn đề của một lục giác lồi nội tiếp và sáu đường tròn Thebault.

Cho lục giác $ABCDEF$ lồi nội tiếp đường tròn $(O)$. Gọi $A_1,B_1,C_1,D_1,E_1,F_1$ lần lượt là các tiếp điểm chung của sáu đường tròn Thebault $(FA,BC,(O))$, $(AB,CD,(O))$, $(BC,DE,(O))$, $(CD,EF,(O))$, $(DE,FA,(O))$, $(EF,AB,(O))$ với $(O)$. Hãy chứng minh $A_1D_1, B_1E_1, C_1F_1$ đồng quy.

http://tube.geogebra.org/m/1352263

Hình vẽ của mở rộng định lý Lester(#20).

Ký hiệu trong hình vẽ. $X_4$ là trực tâm, $X_{3}$ là tâm ngoại tiếp, $X_{13}$, $X_{14}$ là hai điểm Fermats

Mở rộng định lý Napoleon liên hệ với đường Kieppert hyperbola.

Cho $ABC$ là một tam giác, $F$ là điểm Fermat(thứ nhất hoặc thứ 2). $K$ là điểm nằm trên đường hyperbol Kiepert, $P$ là điểm nằm trên đường thẳng $FK$. $A_0$ là giao điểm của đường thẳng qua $P$ vuông góc với $BC$ và đường thẳng $AK$, định nghĩa $B_0,C_0$ tương tự. Chứng minh rằng $A_0B_0C_0$ là tam giác đều vị tự của tam giác Napoleon (ngoài hoặc trong)