có ai biết cách làm dạng này ko?
a)Cho a+b+c=1. Tìm max A= xab+ ybc +zca (x,y,z là các stn)
b ) Cho ab+ bc+ca=1 .tìm min B= xa^2+ yb^2 +zc^2 (x,y,z là các stn)
Tks nh
Câu a dùng tam thức, câu b dùng Cauchy-Schwarz.
Có 785 mục bởi Nguyenhuyen_AG (Tìm giới hạn từ 28-04-2020)
 Đã gửi bởi
Nguyenhuyen_AG
on 16-08-2017 - 22:41
trong
Bất đẳng thức và cực trị
Đã gửi bởi
Nguyenhuyen_AG
on 16-08-2017 - 22:41
trong
Bất đẳng thức và cực trị
có ai biết cách làm dạng này ko?
a)Cho a+b+c=1. Tìm max A= xab+ ybc +zca (x,y,z là các stn)
b ) Cho ab+ bc+ca=1 .tìm min B= xa^2+ yb^2 +zc^2 (x,y,z là các stn)
Tks nh
Câu a dùng tam thức, câu b dùng Cauchy-Schwarz.
 Đã gửi bởi
Nguyenhuyen_AG
on 09-02-2016 - 15:04
trong
Bất đẳng thức và cực trị
Đã gửi bởi
Nguyenhuyen_AG
on 09-02-2016 - 15:04
trong
Bất đẳng thức và cực trị
x,y,z là các số thực dương thỏa mãn x≥y≥z và x+y+z=3
Min P= $\frac{x}{z}$ + $\frac{z}{y}$ + 3y
Ta thấy nếu $x=y=z=1$ thì $P= 5$ như vậy nếu ta chứng minh được $P \geqslant 5$ thì đây cũng chính là giá trị nhỏ nhất của bài toán.
Viết $P$ lại dưới dạng thuần nhất như sau
\[P=\frac{x}{z}+ \frac{z}{y}+\frac{9y}{x+y+z}.\]
Áp dụng bất đẳng thức Cauchy-Schwarz, ta có
\[P \geqslant \frac{(x+z+3y)^2}{zx+yz+y(x+y+z)}.\]
Ta cần chứng minh
\[(x+z+3y)^2 \geqslant 5[zx+yz+y(x+y+z)]. \quad (1)\]
Do $x \geqslant y \geqslant z$ nên tồn tại hai số thực không âm $a,\,b$ sao cho $x = a + z,\,y = b+z.$ Thay các giá trị này vào (1) và thu gọn lại ta được
\[a^2+ab+4b^2+5bz \geqslant 0.\]
Hiển nhiên đúng, như vậy $P = 5$ là giá trị nhỏ nhất cần tìm.
 Đã gửi bởi
Nguyenhuyen_AG
on 23-03-2017 - 15:13
trong
Bất đẳng thức và cực trị
Đã gửi bởi
Nguyenhuyen_AG
on 23-03-2017 - 15:13
trong
Bất đẳng thức và cực trị
Anh có Tool hỗ trợ không ạ chứ em thấy anh biến đổi các bài phức tạp đều về SOS và chỉ cần tiêu chuẩn cơ bản
Anh đã viết nó thành một chương trình chạy trên nền Maple.
Mình chỉ đoán thôi bạn chứ dấu bằng xảy ra xấu thì mình nghĩ phải cân bằng hệ số mà phương pháp ấy khá phức tạp về bước giải phương trình mà không có máy thính thì chịu
Có thể tìm dấu bằng dễ dàng bằng cách viết biểu thức lại dưới dạng
\[(3x^2+4y^2+5z^2)(3x+2y+z) = 72\left(\frac{3}{12}x^2+\frac{4}{12}y^2+\frac{5}{12}z^2\right)\left(\frac{3}{6}x+\frac{2}{6}y+\frac{1}{6}z\right),\] rồi dùng bất đẳng thức AM-GM suy rộng.
 Đã gửi bởi
Nguyenhuyen_AG
on 22-03-2017 - 13:48
trong
Bất đẳng thức và cực trị
Đã gửi bởi
Nguyenhuyen_AG
on 22-03-2017 - 13:48
trong
Bất đẳng thức và cực trị
x, y, z là các số thực thỏa mãn: $2xyz=3x^{2}+4y^{2}+5z^{2}$. Tìm giá trị nhỏ nhất: $P=3x+2y+z$
Ta có
\[\begin{aligned} \frac{(3x^2+4y^2+5z^2)(3x+2y+z)}{2xyz} - 36 = \frac{(9x+8y+z)(x-y)^2+(19x+3z)(y-z)^2+2(8y+z)(z-x)^2}{2xyz}.\end{aligned}\]
Đẳng thức xảy ra khi $x=y=z.$
 Đã gửi bởi
Nguyenhuyen_AG
on 22-03-2017 - 20:55
trong
Bất đẳng thức và cực trị
Đã gửi bởi
Nguyenhuyen_AG
on 22-03-2017 - 20:55
trong
Bất đẳng thức và cực trị
Cho em hỏi làm sao mà tách được như vậy ạ, đây là phương pháp gì ạ?
Kỹ thuật này dùng phương pháp đồng nhất hệ số. Đầu tiên dùng bất đẳng thức AM-GM hoặc AM-GM suy rộng ta sẽ tìm được giá trị nhỏ nhất khi $x=y=z$ và bài toán quy về chứng minh
\[(3x^2+4y^2+5z^2)(3x+2y+z) - 72xyz \geqslant 0.\]
Vì vế trái là một đa thức bậc $3$ không hoán vị cũng không đối xứng nên nếu biểu diễn được dưới dạng sos thì nó có thể có dạng
\[\begin{aligned}(3x^2+4y^2&+5z^2)(3x+2y+z) - 72xyz = \\&= (m_1x+m_2y+m_3z)(x-y)^2 + (m_4x+m_5y+m_6z)(y-z)^2 + (m_7x+m_8y+m_9z)(z-x)^2.\end{aligned}\]
Đồng nhất hệ số hai vế giải hệ phương trình tìm nghiệm $m_i \geqslant 0,\,i=1,\,2,\,\ldots,\,9.$ Chú ý rằng hệ phương trình thu được là hệ phương trình tuyến tính và có thể có nhiều nghiệm nên phân tích trên không phải là duy nhất.
Có thể xem thêm ở đây.
 Đã gửi bởi
Nguyenhuyen_AG
on 23-06-2016 - 13:52
trong
Bất đẳng thức và cực trị
Đã gửi bởi
Nguyenhuyen_AG
on 23-06-2016 - 13:52
trong
Bất đẳng thức và cực trị
Cho em hỏi là anh dùng thuật toán như thế nào để phân tích ra các hệ số không âm vậy ạ? Em phân tích ra dạng SOS mà các hệ số có âm có dương khá là khó đánh giá
Anh dùng hệ số bất định. ![]()
 Đã gửi bởi
Nguyenhuyen_AG
on 25-05-2016 - 14:02
trong
Bất đẳng thức và cực trị
Đã gửi bởi
Nguyenhuyen_AG
on 25-05-2016 - 14:02
trong
Bất đẳng thức và cực trị
Bài toán 6. Cho $a,b,c$ là các số thực thỏa mãn $ab+bc+ca=3$. Chứng minh\[4(a^4+b^4+c^4)+11abc(a+b+c)\ge 45.\]
Nếu bất đẳng thức này đúng thì bất đẳng thức sau cũng đúng
\[4(a^4+b^4+c^4)+11abc(a+b+c) \geqslant 5(ab+bc+ca)^2. \quad (1)\]
Cho $a=1,b=1$ thì $(1)$ trở thành
\[8+4c^4+11c(c+2) \geqslant 5(2c+1)^2,\]
hay là
\[(2c+3)(2c+1)(c-1)^2 \geqslant 0.\]
Dễ thấy bất đẳng thức này không phải luôn đúng.
 Đã gửi bởi
Nguyenhuyen_AG
on 26-05-2016 - 23:35
trong
Bất đẳng thức và cực trị
Đã gửi bởi
Nguyenhuyen_AG
on 26-05-2016 - 23:35
trong
Bất đẳng thức và cực trị
Bài toán 10. Cho $a, b, c >0$. Chứng minh rằng:
\[(a+b+c)\left(\dfrac{a}{b^2+c^2} + \dfrac{b}{c^2+a^2} + \dfrac{c}{a^2+b^2}\right) \geq 4+ \dfrac{4a^2b^2c^2}{(a^2+b^2)(b^2+c^2)(c^2+a^2)}. \quad (1)\]
Lời giải bài 10. Bất đẳng thức $(1)$ tương đương với
\[(a+b+c)\left [\sum a(a^2+b^2)(a^2+c^2) \right ] \geqslant 4(a^2+b^2)(b^2+c^2)(c^2+a^2)+4a^2b^2c^2.\]
Chuyển về pqr như sau
\[p\left [(3p^2-5q)r+p(p^2-3q)(p^2-2q) \right ] \geqslant 4(p^2-2q)(q^2-2pr),\]
thu gọn thành
\[p(11p^2-21q)r+(p^2-4q)(p^2-2q)(p^2+q) \geqslant 0. \quad (2)\]
Chú ý rằng $p^2 \geqslant 3q \geqslant 2q$ cho nên
Ta có điều phải chứng minh.
 Đã gửi bởi
Nguyenhuyen_AG
on 16-06-2016 - 23:59
trong
Bất đẳng thức và cực trị
Đã gửi bởi
Nguyenhuyen_AG
on 16-06-2016 - 23:59
trong
Bất đẳng thức và cực trị
phân tích hình như bị sai á anh
Anh gõ nhầm $+1$ thành $-1.$ Đã sửa. ![]()
 Đã gửi bởi
Nguyenhuyen_AG
on 28-05-2016 - 18:48
trong
Bất đẳng thức và cực trị
Đã gửi bởi
Nguyenhuyen_AG
on 28-05-2016 - 18:48
trong
Bất đẳng thức và cực trị
Một lời giải khác cho bài toán 14:
Đặt $\frac{a+b}{2}=z, \frac{b+c}{2}=x, \frac{a+c}{2}=y$. Ta có $x+y+z=1$, sử dụng AM-GM ta có $\frac{a+b}{ab+1} \geq \frac{a+b}{(\frac{a+b}{2})^2+1}=\frac{2z}{z^2+1}$. Phần còn lại ta chứng minh $\frac{x}{x^2+1} +\frac{y}{y^2+1} +\frac{z}{z^2+1} \geq \frac{9}{10}$. Đó là BĐT Polish 96 nổi tiếng.
Bất đẳng thức trong đề thi của Ba Lan có chiều ngược lại.
 Đã gửi bởi
Nguyenhuyen_AG
on 26-06-2016 - 11:52
trong
Bất đẳng thức và cực trị
Đã gửi bởi
Nguyenhuyen_AG
on 26-06-2016 - 11:52
trong
Bất đẳng thức và cực trị
Đẳng thức này đúng, chú ý $a+b+c=3.$
Cho $a=1,\,b=\frac{1}{2},\,c=\frac{3}{2}$ thì $a+b+c=3$
\[6\left(\dfrac{a}{b}+\dfrac{b}{c}+\dfrac{c}{a}\right)+3-7(a^2+b^2+c^2) = \frac{3}{2},\]
và
\[\dfrac{2}{3} \cdot \left[\dfrac{(2b-c)^2(a-b)^2}{bc}+\dfrac{(2c-a)^2(b-c)^2}{ca}+\dfrac{(2a-b)^2(c-a)^2}{ab} \right] = \frac{31}{12}.\]
Bài 35 có thể chứng minh dựa vào đẳng thức sau, chú ý là có thể tìm ra và tính toán bằng tay chứ không phải dùng máy tính:
Tất nhiên là làm hoàn toàn bằng tay, những phân tích kiểu này anh Cẩn cũng đã từng hướng dẫn trong tạp chí Epsilon số 1.
 Đã gửi bởi
Nguyenhuyen_AG
on 31-05-2016 - 14:42
trong
Bất đẳng thức và cực trị
Đã gửi bởi
Nguyenhuyen_AG
on 31-05-2016 - 14:42
trong
Bất đẳng thức và cực trị
Bài toán 21. (AoPS) Cho các số thực không âm $a,b,c$ thỏa mãn $a+b+c=3.$ Chứng minh rằng
\[\sqrt{4a^4+5abc}+\sqrt{4b^4+5abc}+\sqrt{4c^4+5abc} \geq 9.\]
Lời giải bài 21. Vì \[\sqrt{4a^4+5abc}-2a^2 = \frac{5abc}{2a^2+\sqrt{4a^4+5abc}},\]
và $9 = \sum a^2 + 2\sum bc,$ nên bất đẳng thức cần chứng minh tương đương với
\[5abc \sum \frac{1}{2a^2+\sqrt{4a^4+5abc}} \geqslant 2(ab+bc+ca) -(a^2+b^2+c^2).\]
Áp dụng bất đẳng thức Schur bậc ba
\[2(ab+bc+ca) -(a^2+b^2+c^2) \leqslant \frac{9abc}{a+b+c} = 3abc,\]
ta quy bài toán về chứng minh
\[\sum \frac{1}{2a^2+\sqrt{4a^4+5abc}} \geqslant \frac{3}{5}.\]
Theo bất đẳng thức AM-GM thì $bc \leqslant \frac{(b+c)^2}{4} = \frac{(3-a)^2}{4},$ và
\[\sqrt{a(4a^3+5bc)} \leqslant \frac{1}{6}\left [ 9a+(4a^3+5bc) \right ] \leqslant \frac{1}{24}(16a^3+5a^2+6a+45).\]
nên ta chỉ cần chỉ ra
\[\sum \frac{24}{16a^3+53a^2+6a+45} \geqslant \frac{3}{5}.\]
Bất đẳng thức này được suy ta từ bất đẳng thức sau và hai bất đẳng thức nữa tương tự
\[\frac{24}{16a^3+53a^2+6a+45} \geqslant \frac{1}{5} - \frac{4}{15}(a-1).\]
Nhưng điều này hiển nhiên vì nó tương đương với
\[\frac{(64a^2+228a+45)(a-1)^2}{15(16a^3+53a^2+6a+45)} \geqslant 0.\]
Bài toán được chứng minh.
 Đã gửi bởi
Nguyenhuyen_AG
on 28-05-2016 - 22:59
trong
Bất đẳng thức và cực trị
Đã gửi bởi
Nguyenhuyen_AG
on 28-05-2016 - 22:59
trong
Bất đẳng thức và cực trị
Bài 14:(Micheal Rosenberg)cho $a,b,c$ dương thỏa a+b+c=1 chứng minh
$\frac{a+b}{ab+1}+\frac{b+c}{bc+1}+\frac{c+a}{ca+1}\geq \frac{9}{5}$
Lời giải bài 14. Viết bất đẳng thức lại dưới dạng
\[(a+b+c)\sum \frac{a+b}{(a+b+c)^2+ab}\geqslant \frac{9}{5}.\]
Chuyển về pqr như sau
\[p^4(p^2-4q)+2p(3p^2+5q)r-9r^2 \geqslant 0,\]
hay là
\[2p(11p^2+6q)r+(p^2-4q)(3p^4-q^2)+\left [ p^2q^2-4q^3+2p(9q-2p^2)r-27r^2 \right ] \geqslant 0.\]
Vì
\[p^2q^2-4q^3+2p(9q-2p^2)r-27r^2 = (a-b)^2(b-c)^2(c-a)^2 \geqslant 0,\]
nên ta chỉ cần chứng minh
\[2p(11p^2+6q)r+(p^2-4q)(3p^4-q^2) \geqslant 0. \quad (1)\]
Do $p^2 \geqslant 3q > 0$ vì thế
Chứng minh hoàn tất.
 Đã gửi bởi
Nguyenhuyen_AG
on 28-05-2016 - 23:09
trong
Bất đẳng thức và cực trị
Đã gửi bởi
Nguyenhuyen_AG
on 28-05-2016 - 23:09
trong
Bất đẳng thức và cực trị
$$(a^{2}+ab+b^{2})(b^{2}+bc+c^{2})(c^{2}+ca+a^{2})\geq \frac{1}{3}(2\sum a^{2}+\sum ab)(ab+bc+ca)^{2}$$
Bất đẳng thức này đúng mọi số thực $a,b,c$ bất kỳ vì nó tương đương với
\[\frac{1}{3}\left [ a^2b^2+b^2c^2+c^2a^2-abc(a+b+c) \right ](a+b+c)^2 \geqslant 0.\]
\begin{array}{| l | l |} \hline \text{HDTterence2k} & 1\\ \hline \text{hoanglong2k} & 3\\ \hline \text{Gachdptrai12} & 7\\ \hline \text{Nguyenhuyen_AG} & 5\\ \hline \text{fatcat12345} & 4\\ \hline \text{lenhatsinh3} & 1\\ \hline \text{tuanyeubeo2000} & 1\\ \hline \text{Ngockhanh99k48} & 1 \\ \hline \text{Dinh de Tai} & 1\\ \hline \end{array}
 Đã gửi bởi
Nguyenhuyen_AG
on 16-06-2016 - 21:01
trong
Bất đẳng thức và cực trị
Đã gửi bởi
Nguyenhuyen_AG
on 16-06-2016 - 21:01
trong
Bất đẳng thức và cực trị
Bài 35 (VQBC). Cho $a,b,c>0.$ Chứng minh rằng $$2(\frac{a}b{+\frac{b}c{+\frac{c}{a}}})+1\geq \frac{21(a^{2}+b^{2}+c^{2})}{(a+b+c)^{2}}.$$
Ta có
\[2\left(\frac{a}b{+\frac{b}c{+\frac{c}{a}}}\right)+1-\frac{21(a^{2}+b^{2}+c^{2})}{(a+b+c)^{2}} = \frac{2\displaystyle \sum a(a-b)^2(b-2c)^2}{abc(a+b+c)^2} \geqslant 0.\]
Từ đó suy ra điều phải chứng minh.
 Đã gửi bởi
Nguyenhuyen_AG
on 29-05-2016 - 21:19
trong
Bất đẳng thức và cực trị
Đã gửi bởi
Nguyenhuyen_AG
on 29-05-2016 - 21:19
trong
Bất đẳng thức và cực trị
Bài toán 16. (Võ Quốc Bá Cẩn,Trần Quang Hùng) Cho $a,b,c$ là các số thực không âm thỏa $a+b+c=1$. Chứng minh $$\dfrac{1}{\sqrt{(a^2+ab+b^2)(a^2+ac+c^2)}}+\dfrac{1}{\sqrt{(b^2+bc+c^2)(b^2+ba+a^2)}}+\dfrac{1}{\sqrt{(c^2+ca+a^2)(c^2+cb+b^2)}}\geq 4+\dfrac{8}{\sqrt{3}}$$
Lời giải bài 16. Đặt $k=\frac{2}{\sqrt{3}}$ áp dụng bất đẳng thức Holder, ta có
\[\left [\sum\frac{1}{\sqrt{(a^2+ab+b^2)(b^2+bc+c^2)}} \right ]^2 \geqslant \frac{(k+1)^3(a+b+c)^3}{\displaystyle \sum (a^2+ab+b^2)(b^2+bc+c^2)\left [ (k+1)a+b+c \right ]^3}.\]
Chú ý rằng $\left (4+\frac{8}{\sqrt{3}} \right )^2 = 16(k+1)^2$ nên ta quy bài toán về chứng minh
\[(k+1)(a+b+c)^7 \geqslant \sum (a^2+ab+b^2)(b^2+bc+c^2)\left [ (k+1)a+b+c \right ]^3.\]
Chuyển về pqr như sau
\[Ar + p(p^2-4q)B \geqslant 0. \quad (1)\]
Trong đó
\[\left\{\begin{aligned}A & = \frac{16}{3}(102-83k)p^4+192(7k-8)p^2q+128(6-5k)q^2, \\ B &= \frac{729-615k}{81423}\left [ 9047p^4+4(6876k+251)qp^2+64(1-297k)q^2 \right ]\end{aligned}\right.\]
Ta sẽ chứng minh $A,\,B \geqslant 0.$ Thật vậy, đặt $p^2 = (t+3)q$ với $t \geqslant 0,$ ta được
\[\left\{\begin{aligned}A & = \frac{16\left [ (102-83k)t^2+(324-246k)t+198-111k \right ]p^4}{3(t+3)^2} \geqslant 0, \\ B& = \frac{(243-205k)\left [ 9047t^2+(27504k+55286)t+63504k+84499 \right ]p^4}{27141(t+3)^2} \geqslant 0.\end{aligned}\right.\]
Như vậy
Vậy ta có điều phải chứng minh.
P/s. Anh nghĩ lời giải của Long không đúng, bài này chắc có kiểu dồn biến theo kiểu thừa trừ của anh Cẩn. Còn điều kiện của bài 17 là dương hay không âm nhỉ ?
 Đã gửi bởi
Nguyenhuyen_AG
on 21-06-2016 - 20:13
trong
Bất đẳng thức và cực trị
Đã gửi bởi
Nguyenhuyen_AG
on 21-06-2016 - 20:13
trong
Bất đẳng thức và cực trị
hình như cái phân tích thế nào ấy em phân tích nó ra khác và ko lớn hơn 0 anh xem lại dùm em cảm ơn
Anh đã kiểm tra lại và thấy nó đúng ![]()
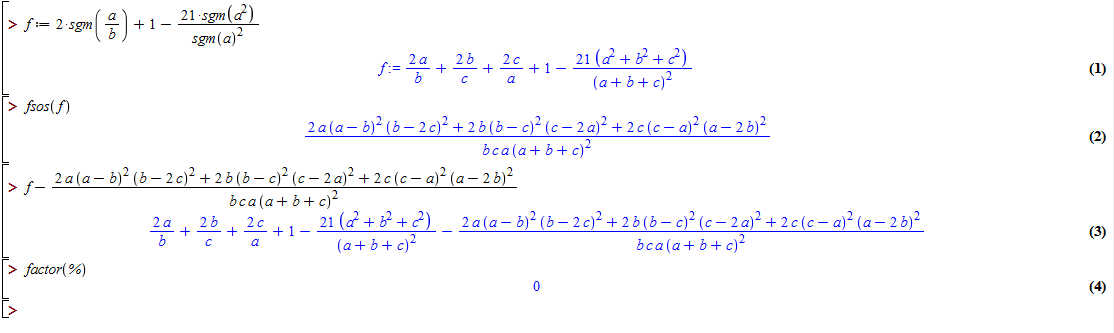
 Đã gửi bởi
Nguyenhuyen_AG
on 29-05-2016 - 22:07
trong
Bất đẳng thức và cực trị
Đã gửi bởi
Nguyenhuyen_AG
on 29-05-2016 - 22:07
trong
Bất đẳng thức và cực trị
lời giải của Long em nghĩ nó đúng mà với lại đó là dồn biến thừa trừ luôn mà anh Huyện
À anh nhìn nhầm.
 Đã gửi bởi
Nguyenhuyen_AG
on 25-06-2016 - 21:58
trong
Bất đẳng thức và cực trị
Đã gửi bởi
Nguyenhuyen_AG
on 25-06-2016 - 21:58
trong
Bất đẳng thức và cực trị
Bài 35 có thể chứng minh dựa vào đẳng thức sau, chú ý là có thể tìm ra và tính toán bằng tay chứ không phải dùng máy tính:
http://artofproblems...231645p3507509
An interesting proof for you, manilo!
\[{ 6\left(\dfrac{a}{b}+\dfrac{b}{c}+\dfrac{c}{a}\right)+3-7(a^2+b^2+c^2)=\dfrac{2}{3} \cdot \left[\dfrac{(2b-c)^2(a-b)^2}{bc}+\dfrac{(2c-a)^2(b-c)^2}{ca}+\dfrac{(2a-b)^2(c-a)^2}{ab} \right].}\]
Đẳng thức này sai.
 Đã gửi bởi
Nguyenhuyen_AG
on 24-05-2016 - 22:52
trong
Bất đẳng thức và cực trị
Đã gửi bởi
Nguyenhuyen_AG
on 24-05-2016 - 22:52
trong
Bất đẳng thức và cực trị
Bài toán 1. (Võ Quốc Bá Cẩn) Cho $a,b,c\geq 0$. Chứng minh rằng \[\sqrt{\dfrac{a(b+c)}{b^2+c^2}}+\sqrt{\dfrac{b(c+a)}{c^2+a^2}}+\sqrt{\dfrac{c(a+b)}{a^2+b^2}}\geq 2\]
Lời giải bài 1. Áp dụng bất đẳng thức Holder
\[\left [\sum \sqrt{\dfrac{a(b+c)}{b^2+c^2}} \right ]^2 \sum \frac{a^2(b^2+c^2)}{b+c} \geqslant (a+b+c)^3.\]
Ta quy bài toán về chứng minh
\[(a+b+c)^3 \geqslant 4\sum \frac{a^2(b^2+c^2)}{b+c}.\]
Dễ thấy
\[\frac{a^2(b^2+c^2)}{b+c} \leqslant \frac{a^2(b+c)^2}{b+c} = a^2(b+c),\]
nên ta chỉ cần chỉ ra
\[(a+b+c)^3 \geqslant 4\sum a^2(b+c),\]
hay là
\[a^3+b^3+c^3+6abc \geqslant \sum a^2(b+c).\]
Hiển nhiên đúng theo bất đẳng thức Schur bậc ba.
 Đã gửi bởi
Nguyenhuyen_AG
on 26-06-2016 - 22:29
trong
Bất đẳng thức và cực trị
Đã gửi bởi
Nguyenhuyen_AG
on 26-06-2016 - 22:29
trong
Bất đẳng thức và cực trị
lời giải của bạn là lời giải được lấy từ http://www.artofprob...h507278p2850887
Sao em có thể khẳng định như vậy ?
 Đã gửi bởi
Nguyenhuyen_AG
on 25-05-2016 - 13:19
trong
Bất đẳng thức và cực trị
Đã gửi bởi
Nguyenhuyen_AG
on 25-05-2016 - 13:19
trong
Bất đẳng thức và cực trị
Bài toán 5. (Phạm Kim Hùng) Cho các số thực $a,b,c$ dương. Tìm hằng số $k$ tốt nhất sao cho bất đẳng thức sau luôn đúng\[\dfrac{a^3+b^3+c^3}{(a+b)(b+c)(c+a)}+\dfrac{k(ab+bc+ca)}{(a+b+c)^2}\geq \dfrac{3}{8}+\dfrac{k}{3}\]
Lời giải bài 5. Cho $a=b=1,c=\frac{1}{1+\sqrt{3}}$ ta được $$k \leqslant \frac{27+18\sqrt{3}}{8}.$$ Đặt $k=\frac{27+18\sqrt{3}}{8}$ ta sẽ chứng minh đây là giá trị lớn nhất cần tìm. Thật vậy, viết bất đẳng thức lại dưới dạng
\[\dfrac{(a+b+c)^3}{(a+b+c)(ab+bc+ca)-abc}+\dfrac{k(ab+bc+ca)}{(a+b+c)^2} \geqslant \dfrac{27}{8}+\dfrac{k}{3}. \quad (1)\]
Chuẩn hóa $a+b+c=3$ khi đó tồn tại số thực $0 \leqslant t < 1$ để $a^2+b^2+c^2=3+6t^2$ và (1) trở thành
\[\dfrac{27}{9(1-t^2)-abc}+\dfrac{k(1-t^2)}{3} \geqslant \dfrac{27}{8}+\dfrac{k}{3}.\]
Chú ý rằng $abc \geqslant (1-2t)(1+t)^2$ nên ta chỉ cần chứng minh
\[\dfrac{27}{9(1-t^2)-(1-2t)(1+t)^2}+\dfrac{k(1-t^2)}{9} \geqslant \dfrac{27}{8}+\dfrac{k}{3},\]
hay là
\[\frac{t^2\left [ 81(3-t)-8(1+t)(t-2)^2k \right ]}{24(1+t)(t-2)^2} \geqslant 0. \quad (2)\]
Với $k = \frac{27+18\sqrt{3}}{8}$ thì ta có thể phân tích $(2)$ thành
\[\frac{3(2\sqrt{3}+3)(2\sqrt{3}-1-t)(t-2+\sqrt{3})^2t^2}{8(1+t)(t-2)^2} \geqslant 0.\]
Hiển nhiên đúng, đẳng thức xảy ra khi và chỉ khi $a=b=c$ hoặc $a=b=c(1+\sqrt{3}).$
 Đã gửi bởi
Nguyenhuyen_AG
on 24-05-2016 - 23:16
trong
Bất đẳng thức và cực trị
Đã gửi bởi
Nguyenhuyen_AG
on 24-05-2016 - 23:16
trong
Bất đẳng thức và cực trị
Bài toán 3. Cho các số thực dương $a,b,c$ thỏa mãn $\dfrac{1}{a^4+1}+\dfrac{1}{b^4+1}=\dfrac{c^4}{c^4+1}$. Chứng minh rằng
\[\dfrac{abc(a+b+c)}{ab+bc+ca}\geq \sqrt{2}\]
Lời giải bài 3. Giả thiết của bài toán tương đương với
\[\sum \frac{1}{a^4+1} = 1.\]
Đặt $a=\frac{1}{x},\,b=\frac{1}{y},\,c=\frac{1}{z}$ thì giả thiết trở trở thành
\[\sum \frac{x^4}{x^4+1}=1,\]
và ta cần chứng minh
\[\frac{xy+yz+zx}{xyz(x+y+z)} \geqslant \sqrt{2}.\]
Vì $3xyz(x+y+z) \leqslant (xy+yz+zx)^2,$ nên ta đưa bài về chứng minh bất đẳng thức mạnh hơn là
\[xy+yz+zx \leqslant \frac{3}{\sqrt{2}}.\]
Nhưng điều này khá hiển nhiên vì
\[1 = \sum \frac{x^4}{x^4+1} \geqslant \frac{(x^2+y^2+z^2)^2}{x^4+y^4+z^4+3} \geqslant \frac{x^4+y^4+z^4+\frac{2}{3}(xy+yz+zx)^2}{x^4+y^4+z^4+3},\]
cho nên
$$x^4+y^4+z^4+\frac{2}{3}(xy+yz+zx)^2 \leqslant x^4+y^4+z^4+3,$$
hay là
\[(xy+yz+zx)^2 \leqslant \frac{9}{2}.\]
Từ đó suy ra điều phải chứng minh.
P/s. Tóm lại giá trị lớn nhất và nhỏ nhất cụ thể của bài 2 là bao nhiêu vậy nhỉ ?
 Đã gửi bởi
Nguyenhuyen_AG
on 29-05-2016 - 23:54
trong
Bất đẳng thức và cực trị
Đã gửi bởi
Nguyenhuyen_AG
on 29-05-2016 - 23:54
trong
Bất đẳng thức và cực trị
Bài toán 17. (Sưu tầm) Cho các số thực không âm $x,y,z$ thỏa mãn $x+y+z=32$. Tìm giá trị lớn nhất của
$$P=x^3y+y^3z+z^3x$$
Lời giải bài 17. Bản chất của bài toán này chính là bất đẳng thức
\[x^3y+y^3z+z^3x \leqslant \frac{27}{256}(x+y+z)^4.\]
Ta sẽ chứng minh kết quả mạnh hơn của Michael Rozenberg
\[x^3y+y^3z+z^3x+\frac{473}{256}xyz(x+y+z) \leqslant \frac{27}{256}(x+y+z)^4,\]
hay là
\[256(x^3y+y^3z+z^3x)+473xyz(x+y+z) \leqslant 27(x+y+z)^4. \quad (1)\]
Giả sử $z = \min\{x,y,z\}$ và đặt $x=a+z,\;y=b+z$ bất đẳng thức (1) trở thành
\[217(a^2-ab+b^2)z^2+(68a^3-269a^2b+499ab^2+68b^3)z+(27a^2+14ab+3b^2)(a-3b)^2 \geqslant 0.\]
Chú ý rằng
\[68a^3-269a^2b+499ab^2+68b^3 = 60a(a^2-5ab+8b^2)+8a^3+31a^2b+19ab^2+68b^3 \geqslant 0.\]
Nên ta có điều phải chứng minh.
 Đã gửi bởi
Nguyenhuyen_AG
on 30-05-2016 - 00:12
trong
Bất đẳng thức và cực trị
Đã gửi bởi
Nguyenhuyen_AG
on 30-05-2016 - 00:12
trong
Bất đẳng thức và cực trị
Bài toán 18. (AoPS) Cho $a,b,c$ là các số không âm thỏa $ab+bc+ca>0$. Chứng minh$\dfrac{1}{a^2+b^2}+\dfrac{1}{b^2+c^2}+\dfrac{1}{c^2+a^2}\geq \dfrac 4{a^2+b^2+c^2}+\dfrac{1}{2(ab+bc+ca)}$
Lời giải bài 18. Bất đẳng thức cần chứng minh tương đương với
\[\dfrac{a^2}{b^2+c^2}+\dfrac{b^2}{c^2+a^2}+\dfrac{c^2}{a^2+b^2} \geqslant 1+\dfrac{a^2+b^2+c^2}{2(ab+bc+ca)},\]
hay là
\[\dfrac{a^2}{b^2+c^2}+\dfrac{b^2}{c^2+a^2}+\dfrac{c^2}{a^2+b^2} \geqslant \dfrac{(a+b+c)^2}{2(ab+bc+ca)}.\]
Hiển nhiên đúng do
\[\sum \frac{a^2}{b^2+c^2} \geqslant \sum \frac{a}{b+c}\geqslant \dfrac{(a+b+c)^2}{2(ab+bc+ca)}.\] Chứng minh hoàn tất.

Community Forum Software by IP.Board
Licensed to: Diễn đàn Toán học
