$\boxed{\text{Lời giải bài toán 17}}$

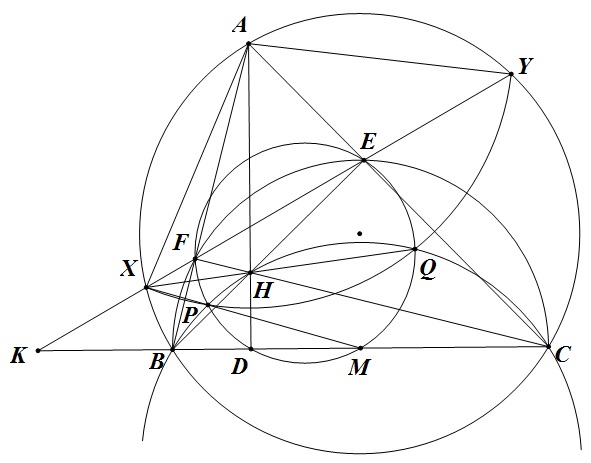
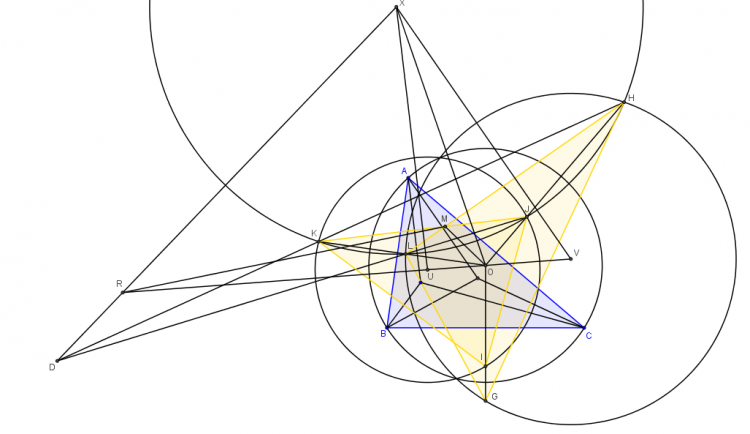
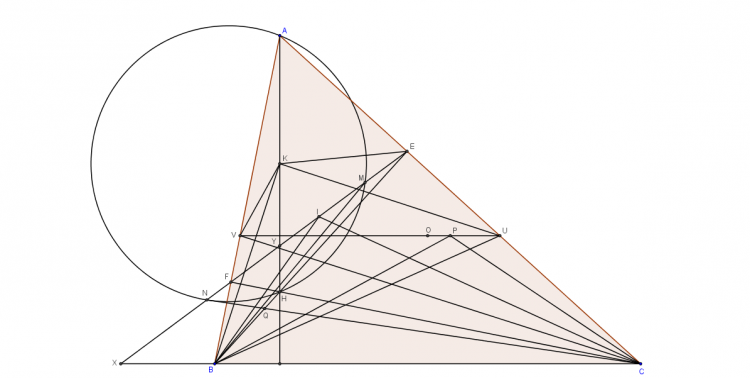
Gọi $X$ và $Y$ là giao điểm của $EF$ và đường tròn ngoại tiếp tam giác $ABC$

xét phép nghịch đảo cực $A$ phương tích $AX^{2}=AY^{2}=AF.AB=AE.AC$ ta có đường tròn $(A;AX)$ trực giao với đường tròn đường kính $BC$ hay$P_{M,(A;AX)}=MB^{2}=MC^{2}$ 

Gọi $K$ là giao điểm $EF$ và $BC$

Gọi $U$ và $V$ là giao điểm của $MX,MY$ và  $(A;AX)$

Do $(K,D,B,C)=-1$ nên theo $Maclaurin$ ta có $KD.KM=KB.KC=KX.KY$ suy ra $XYMD$ nội tiếp $\Rightarrow \angle DXU=\angle DYV$ 

Do $(K,D,B,C)=-1$ nên theo $Newton$ ta có $MX.MU=MB^{2}=MD.MK$ suy ra $XUDK$ nội tiếp

tương tự $YVDK$ nội tiếp

ta có $\angle DKU=\angle DXU=\angle DYV=\angle DKV$ nên $K,U,V$ thẳng hàng

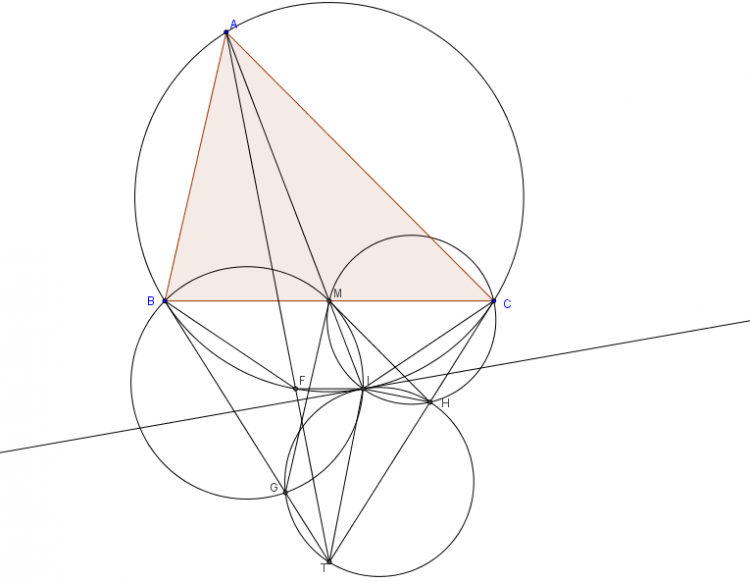
mà $MF^{2}=MD.MK$ nên $\angle DFM=\angle DKF=\angle DUM$ nên $DMFU$ nội tiếp tương tự $DMEV$ nội tiếp

$\Rightarrow $ đường thằng chứa $K,U,V$ chính là trục đẳng phương của đường tròn $Euler$ và   $(A;AX)$

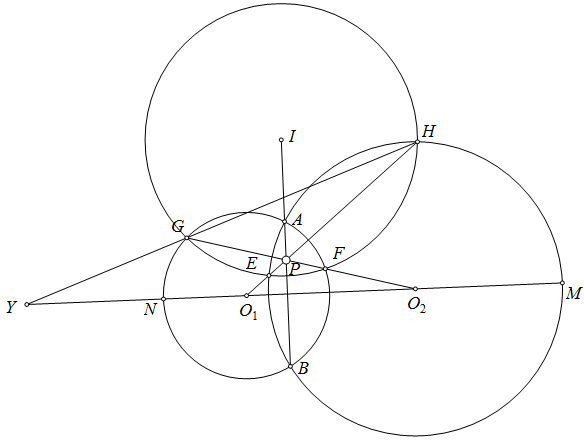
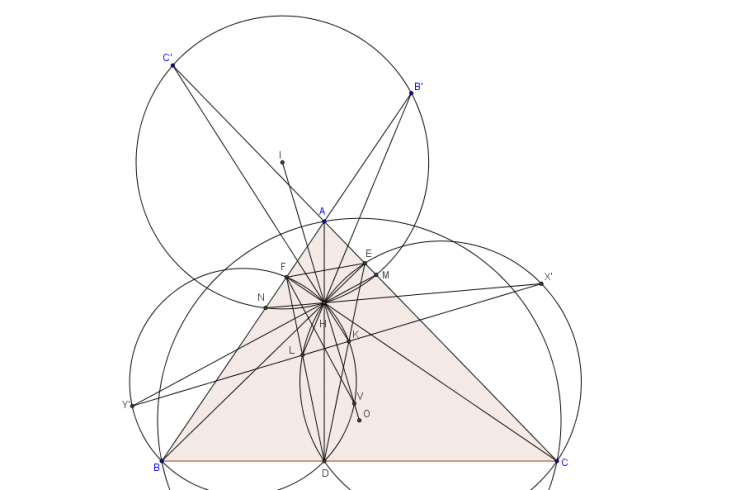
ta có tâm đường tròn $Euler$, tâm $A'$ của $(BHC)$ và $A$ thằng hàng  nên $AA'$ vuông góc  $UV$

mà $KX.KY=KB.KC= KU.KV$ và $K$ thuộc đương thẳng $UV$ nên $(A;AX)$, đường tròn $Euler$ và đường tròn $(BHC)$ có 2 điểm chung là $U,V$

vậy  $U\equiv P,V\equiv Q$

Áp dụng định lý $Brocard$ cho tứ giác $BECF$ nội tiếp ta có $H$ là trực tâm của tam giác $AKM$, mà $A$ là tâm  $(A;AX)$  nên theo định lý $Brocard$ cho tứ giác nội tiếp $XYPQ$ thì $H$ là giao điểm $XQ,YP\Rightarrow XQ$ đi qua $H$

vậy $MP,QH,EF$ đồng quy tại $X$ ta có đpcm.

Mình xin đề xuất $\boxed{\text{Bài toán 18}}$

(Sưu tầm) Cho$\Delta ABC$ nhọn. $M$ là một điểm di động trên cạnh $AB$ và $N$ là trung điểm $AC$. Gọi $P,Q$ là hình chiếu của $A$ trên $MC,MN$. Chứng minh rằng khi $M$ di động trên cạnh $AB$ thì tâm đường tròn ngoại tiếp $\Delta PQN$ nằm trên một đường thẳng cố định.

Xin lỗi thầy và mọi người, bài toán vừa rồi mình lấy trong tài liệu 111 nice geometry problems của diễn đàn Mathscope. không ngờ lại trùng bài viết của thầy Hùng

Mình xin up lại bài khác:

$\boxed{\text{Bài toán 9}}$

Cho $\triangle ABC$ có trực tâm $H$. $P,Q$ bất kì thuộc cạnh $AB,AC$ dựng điểm M sao cho $\triangle MBC$ đồng dạng $\triangle HPQ$ và $M$ cùng phía với $A$ đối với cạnh $BC$. Chứng minh rằng $MH$ vuông góc $PQ$

$\boxed{\text{Lời giải bài toán 8}}$ 

Gọi $N,M$ là giao điểm của $O_{1}O_{2}$ với $ O_{1}$ và $O_{2}$ như hình trên, $H$ là giao điểm thứ 2 của $O_{1}P$ và  $(O_{2})$, $G$ là giao điểm thứ 2 của  $O_{2}P$ và  $(O_{1})$

ta sẽ chứng minh $EM,FN$ và $AB$ đồng quy

ta có $(O_{2}PFG)=(O_{1}PEH)=-1$ nên $EF, GH, O_{1}O_{2}$ đồng quy tại $Y$

Gọi $I$ là điểm sao cho $(IPAB)=-1$ thì $IF,IG$ là tiếp tuyến của $O_{1}$  và $IE,IH$ là tiếp tuyến của $O_{2}$, $I$ thuộc $AB$ là trục đẳng phương của 2 đường tròn nên  $IE=IF=IG=IH$ nên $EFGH$ nội tiếp 

suy ra $EG,FH,O_{1}O_{2}$ đồng quy tại điểm $X$ ( theo định lý Brocard) và $(YXO_{1}O_{2})=-1$ nên $PX, O_{1}F, O_{2}E$ đồng quy.

Áp dụng định lí Ceva để ý $R_{1}^{2}=O_{1}E.O_{1}H $ và $R_{2}^{2}=O_{2}F.O_{2}G$  ta có $\frac{XO_{1}}{XO_{2}}=\frac{O_{1}E}{EP}.\frac{PF}{FO_{2}}=\frac{O_{1}H}{PH}.\frac{GP}{GO_{2}}=\frac{R_{1}^{2}}{R_{2}^{2}}.\frac{GP.O_{2}F}{PH.O_{1}E}=\frac{R_{1}^{2}}{R_{2}^{2}}.\frac{EP.O_{2}F}{FP.O_{1}E}=\frac{R_{1}^{2}}{R_{2}^{2}}.\frac{O_{2}X}{O_{1}X}$

nên $\frac{O_{1}X}{O_{2}X}=\frac{R_{1}}{R_{2}}$ nên $X$ là tâm vị tự trong của 2 đường tròn $\Rightarrow Y$ là tâm vị tự ngoài của 2 đường tròn do $(YXO_{1}O_{2})=-1$ $\Rightarrow $ theo tính chất cơ bản ta có $EFMN$ nội tiếp $\Rightarrow EM,FN,AB$ đồng quy tại tâm đẳng phương $V$ của 3 đường tròn

dễ thấy $EM,FN$  là phân giác $\angle PED$ và  $\angle PFD$ nên $EV, FV$ cũng là phân giác 2 góc này

Từ định lý phân giác ta có điều phải chứng minh.

$$\begin{array}{| l | l |} \hline Ngockhanh99k48 & 1\\ \hline IHateMath & 1\\ \hline fatcat12345 & 2\\ \hline dogsteven & 2\\ \hline baopbc & 3\\ \hline QuangDuong12011998 & 1\\ \hline xuantrandong & 1\\ \hline\end{array}$$

L thuộc đường đối cực của B và M nên BM là đường đối cực của L

=> IL vuông góc BM 

tương tự IK vuông góc CN

ta có đpcm

câu hình ý a khá đơn giản sử dụng $\Delta FIN$ đồng dạng $\Delta IEM$

câu hình b gọi T và H là trung điểm EF và EI, ta có $\Delta FIE$ đồng dạng $\Delta IME$ nên $\Delta FIT$ đồng dạng $\Delta IMH$ nên $\angle FIT = \angle IMH=\angle = \angle MIC =\frac{\angle B}{2}$ nên TI là tiếp tuyến của (L) $=>$  TI là trục đẳng phương của (L) và (K) mà T là trung điểm EF nên dễ suy ra được $EP= FQ$

giai thich cho minh cho nay dc k

Gọi $A_1$ là phần tử có nhiều nhất trong $64$ tập con và $a_1$ là số tập con chứa $A_1$, ta có:

$a_1\geq \frac{64.1008}{2016}=32$

Er,E(theta),E(phi) từ đâu ra vậy ạ

Mình xin phép giải bài 2:

Chuyển mô hình bài toán về bài toán sau đây:

Cho $\Delta ABC$ nội tiếp đường tròn $(O)$ có $H$ là trực tâm. 3 đường cao $AD, BE, CF$. Đường thẳng $HO$ cắt $(FHD)$ tại $V$. $Y$ là điểm thuộc $(FHD)$ sao cho $HY$ vuông góc $FV$. Chứng minh rằng điểm đối xứng của $Y$ qua $HO$ thuộc đường tròn $(DHE)$. 

Giải:

Gọi $K, L$ đối xứng với $F, E$ qua $BE, CF$. $KL$ giao $(FHD)$ và $(EHD)$ lần lượt tại $Y', X'$. Ta sẽ chưng minh $OH$ là đường trung trực của $X'Y'$ và $HY'$ vuông góc $FV$, và từ đó ta chứng minh được $X$ trùng $X'$ và $Y$ trùng $Y'$.

Gọi $B', C'$ đối xứng với $B, C$ qua $CF, BE$. $(I)$ là đường tròn ngoại tiếp $\Delta HB'C'$. Theo $APMO-2010$ thì $I, H, O$ thẳng hàng. Dễ thấy theo phép đối xứng trục thì $B', H, L$ và $C', H, K$ thẳng hàng. và $\overline{HK}.\overline{HC'}=\overline{HF}.\overline{HC}=\overline{HE}.\overline{HB}=\overline{HL}.\overline{HB'}$ do đó theo phép nghịch đảo tâm $H$ phương tích $\overline{HA}.\overline{HD}$ thì $IH$ vuông góc $LK$ tức là $X'Y'$ vuông góc $OH$. Gọi $M, N$ là giao điểm $(I)$ và $AC, AB$ thì theo phép nghịch đảo tâm $H$ phương tích $\overline{HA}.\overline{HD}$ thì $CC' \leftrightarrow (FHD) $, $(I) \leftrightarrow X'Y'$ do đó $M \leftrightarrow Y'$, tương tự $N \leftrightarrow X'$. mà $\angle HC'M=\angle HCA=\angle HBA=\angle HB'N$ nên $HM = HN$. Do đó $HX'=HY'$. mà $OH$ vuông góc $X'Y'$ nên $OH$ là đường trung trực $X'Y'$.

Ta có $\angle HVF+\angle VHY'=\angle HBA+\angle IHM=\angle HC'M+\angle IHM=90$ nên $FV$ vuông góc $HY'$

Do đó $X$ trùng $X'$, $Y$ trùng $Y'$ nên ta có điều phải chứng minh

Bài 1:

Gọi $D, E, F$ là điểm đối xứng của $A$ qua $KL, KN, LM$, ta cần chứng minh $(DEF)$ tiếp xúc $BC$.

Gọi $AP$ là đường đối trung của tam giác $ABC$ với $P$ thuộc $(ABC)$

Thấy rằng $D$ là giao điểm của đường tròn qua $A,B$ tiếp xúc $AC$ và đường tròn qua $A,C$ tiếp xúc $AB$

                 $E$ là giao điểm của đường tròn qua $A,C$ tiếp xúc $BC$ và đường tròn qua $A,P$ tiếp xúc $AC$

                 $F$ là giao điểm của đường tròn qua $A,B$ tiếp xúc $BC$ và đường tròn qua $A,P$ tiếp xúc $AB$

Sử dụng phép hợp phép nghịch đảo cực $A$ phương tích $AB.AC$ và phép đối xứng qua phân giác góc $\angle A$ ta được bài toán sau:

Cho $\Delta ABC$ nội tiếp $(O)$, tiếp tuyến tại $B,C$ giao nhau tại $T$, $M$ là trung điểm BC. $H,G$ thuộc $TC,TB$ sao cho $MH // AC$ và $MG // AB$ . Chứng minh rằng $THG$ tiếp xúc $(O)$.

Chứng minh:

$AM,AT$ giao $(O)$ tại $F,I$. kẻ tiếp tuyến $Ix$ của $(O)$.

Dễ chứng minh $BMIG,CMIH,GTHI$ là các tứ giác nội tiếp

Biến đổi góc như sau ( để ý $IF//BC$)

$\angle HIx=\angle CIH-\angle CIx=\angle HMC-\angle FBT=\angle ACB-\angle FBT=\angle AFB-\angle FBT=\angle BTF=\angle HTI$

Do đó $Ix$ cũng là tiếp tuyến của $THG$, do đó $THG$ tiếp xúc $(O)$.

kho ebook ssdg

http://4share.vn/d/6257575252535653

Mình xin phép giải bài 2:

Ta chuyển bài toán trên thành bài toán tương đương như sau: Cho tam giác ABC, P di động trên BC, đường thẳng qua P vuông góc AB, AC cắt các đường thẳng AC, AB tại E, F. Chứng minh rằng tâm đường tròn ngoại tiếp tam giác PEF thuộc một đường thẳng cố đinh.

Đường thẳng qua B và C lần lượt vuông góc AB và AC cắt AC và AB tại M, N. R, S là trung điểm AM, AN. L, K là trung điểm BM, CN. X, Y đối xứng R, S qua L, K. H, I là trung điểm PE, PF. 

Dễ thấy ACYS và ABXR là hình bình hành nên SY // BX // AC và RX // CY // AB. Theo bổ đề hình thang thì B, I, K thẳng hàng và C, H, L thẳng hàng. Qua I kẻ đường thẳng song song với AC giao XY tại O thì áp dụng liên tiếp định lý talet:

$\frac{YO}{OX}=\frac{KI}{IB}=\frac{CP}{PB}=\frac{CH}{HL}$

mà CY // LX nên HO // CY // LX // AB

Vậy O là tâm đường tròn ngoại tiếp tam giác PEF di động trên đường thẳng XY cố định

Mình xin giải bài 2:

Bổ đề: Cho $\Delta ABC$ tâm ngoại tiếp $O$ và 2 điểm $P,Q$ đẳng giác. $H, I, K$ là tâm ngoại tiếp của các tam giác $PBC, PCA,PAB$. $D, E, F$ là tâm ngoại tiếp các tam giác $QBC, QCA, QAB$. Gọi $(O_{1}),(O_{2})$ là các đường tròn ngoại tiếp tam giác $HIK, DEF$. Khi đó  $O, O_{1}, O_{2}$ thẳng hàng và đường thẳng $O_{1}O_{2}$ song song với $PQ$.

Chứng minh bổ đề: Dễ chứng minh các tứ giác $KFIE, EIHD, DHFK$ là các tứ giác nội tiếp và $O$ là tâm đẳng phương của các đường tròn  $(KFIE), (EIHD), (DHFK)$. Xét phép nghịch đảo phương tích $OH.OD=OI.OE=OF.OK$ biến đường tròn $(HIK)$ thành đường tròn $(DEF)$ nên $O, O_{1}, O_{2}$ thẳng hàng. $KI, EF$ giao nhau tại $X$, $DF, HK$ giao nhau tại $Y$. Thì $XK.XI=XE.XF$ và $YD.YF=YH.YK$ nên đường thẳng $XY$ là trục đẳng phương của  $(O_{1}),(O_{2})$ nên $XY$ vuông góc $O_{1}O_{2}$. Hơn nữa do $X, Y$ là tâm ngoại tiếp của các tam giác $APQ, BPQ$ nên $X, Y$ thuộc trung trực của đoạn thẳng $PQ$ nên $XY$ vuông góc $PQ$ do đó $XY$ song song với đường thẳng qua  $O, O_{1}, O_{2}$.

Trở lại bài toán:

Gọi $I, J, K, G, H, L$ lần lượt là tâm đường tròn ngoại tiếp các tam giác $PBC, PCA, PAB, QBC, QCA, QAB$. Gọi $U, V$ là tâm ngoại tiếp các tam giác $IJK, GHL$. Theo bổ đề ta cần chứng minh $DX, EY, FZ, UV$ đồng quy. $UV, AD$ giao nhau tại $R$; $KJ, HL$ giao nhau tại $M$. Ta có:

$(ROUV)=X(R,O,U,V)=M(O,R,J,L)=-1$ ( áp dụng định lý $Brocard$ và chùm trực giao ). 

Do đó nếu $EY, FZ$ giao $UV$ tại $R', R''$ thì ta có $(ROUV)=(R'OUV)=(R''OUV)=-1$ nên $R, R', R''$ trùng nhau. 

Ta có điều phải chứng minh

Bài 2

Lời giải bài 2 của mình

Bổ đề: Cho $\Delta ABC$, 2 điểm $P,Q$ sao cho $P$ nằm ở miền trong $\Delta ABC$ và $BPCQ$ là hình bình hành. khi đó $BP,CP$ đối song $\angle A$ khi và chỉ khi $AP,AQ$ đẳng giác $\angle A$

Chứng minh: Dựng hình bình hành $ACPR$

Giả sử $BP,CP$ đối song thì $\angle ABP=\angle ACP=\angle ARP$ khi đó $ARBP$ nội tiếp nên $\angle BAP=\angle BRP=\angle CAQ$ do đó $AP,AQ$ đẳng giác. 

Chiều ngược lại chứng minh tương tự 

Trở lại bài toán: 

Lấy $P,Q$ đối xứng với $N,M$ qua trung điểm $L$ của $BC$. Áp dụng bổ đề:

Do $BM,CM$ đối song góc $A$ nên $AM,AQ$ đẳng giác góc $A$.

Do $BP,CP$ đối song góc $A$ nên $AN,AP$ đẳng giác góc $A$. 

vậy nên $AM,AQ$ đẳng giác $\angle PAN$, áp dụng bổ đề 1 lần nữa được $PM,NM$ đối song góc $\angle PAN$.

Dựng hình bình hành $AH'MP$ được $H'AMN$ nội tiếp do $\angle AH'M=\angle APM=\angle ANM$

và $AH'$ vuông góc $BC$ nên $H$ trùng $H'$.

Vậy $AH=MP=2KL$

Lời giải bài $2$ của mình dài và chưa hay  

Bổ đề: Trên đường thẳng $d$, lấy các điểm $X,Y,E,F,M,N,I$ sao cho $(XYFE)=-1$, $I$ là trung điểm $EF$, $\overline{YM}.\overline{YN}=\overline{YX}.\overline{YI}$. Khi đó ta có $(MFIX)=(NEXI)$

Chứng minh bổ đề: Gọi tọa độ các điểm $X,E,F,M,N,I$ trên đường thẳng $d$ là $x,e,f,m,n,i$, chọn $Y$ làm gốc tọa độ.

Ta có (dễ thấy) :  $i=\frac{e+f}{2}$

                           $mn=x(\frac{e+f}{2})$

                           $x=\frac{2ef}{e+f}$

Biến đổi: $(MFIX)=(NEXI)\Leftrightarrow \overline{IM}.\overline{IN}.\overline{XE}.\overline{XF}=\overline{XM}.\overline{XN}.\overline{IE}.\overline{IF}\Leftrightarrow (m-\frac{e+f}{2})(n-\frac{e+f}{2})(x-e)(x-f)=-(x-m)(x-n)\frac{(e-f)^{2}}{4}\Leftrightarrow (\frac{(e+f)^{2}}{4}-\frac{(m+n)(e+f)}{2}+mn)=-(x^{2}-x(m+n)+mn)(\frac{(e-f)^{2}}{4})$

Thay  $mn=x(\frac{e+f}{2})$ vào ta có $\frac{e+f}{2}.(x-e)(x-f)=-x.\frac{(e-f)^{2}}{4}$, tiếp tục thay  $x=\frac{2ef}{e+f}$ vào ta được đẳng thức cuối cùng đúng, suy ra điều phải chứng minh.

Trở lại bài toán

Gọi $K$ là trung điểm $AH$, $I$ là trung điểm $EF$, đường thẳng $EF$ giao $BC,AH$ tại $X,Y$, đường thẳng qua $K$ vuông góc $BK, CK$ giao $AC,AB$ tại $U,V$.

Dễ thấy $BKEU$ là tứ giác nội tiếp, nên $\angle KBU=\angle KEA=\angle KAE=\angle HBC\Rightarrow \angle KBE=\angle UBC$

Mà $\angle ABH=\angle OBC$ nên $\angle ABK=\angle OBU$, do đó $O,K$ đẳng giác trong $\Delta ABU$, nên $\angle OUB=\angle KUA=\angle KBE=\angle UBC$ do đó $OU$ song song $BC$. Mặt khác hai tam giác $BHA,BFE$ đồng dạng có $K,I$ là trung điểm của 2 cạnh tương ứng $HA,FE$ nên $\angle KBE=\angle IBA$ nên $\angle UBC=\angle IBA$

Chứng minh tương tự ta cũng được $\angle ICA=\angle VCB$

Do $OU,OV$ song song $BC$ nên $P,U,O,V$ thẳng hàng, nên $B(CUPV)=C(BUPV)$, xét phép đối xứng qua phân giác góc $B$ và phép chiếu xuyên tâm $B$ lên đường thẳng $EF$ thì $B(CUPV)=B(AIQC)=(FIMX)$, tương tự $C(BUPV)=C(ABQI)=(EXNI)$

Do đó $(FIMX)=(EXNI) \Rightarrow (MFIX) = (NEXI )$

Gọi đường tròn $(AMH)$ giao $EF$ tại $N'$ thì theo bổ đề ta có $(MFIX)=(N'EXI)$, vậy $N$ trùng $N'$

Dễ thấy $(XYFE)=-1$ do đó $(YXFE)=-1$, áp dụng hệ thức $Maclaurin$ thì $\overline{YI}.\overline{YX}=\overline{YE}.\overline{YF}$

Vậy $\overline{YM}.\overline{YN}=\overline{YX}.\overline{YI}=\overline{YH}.\overline{YA}$ nên $A,H,M,N$ cùng thuộc 1 đường tròn.

Mình cũng sử dụng bổ đề $2$ của bạn, mình chứng minh nó bằng phép vị tự. 

Kẻ đường kính $AM$. 

Để ý nếu đường tròn ngoại tiếp tam giác $AEF$ cắt $\odot (O)$ tại điểm $X$ thì theo bổ đề $2$: $X,K,I,M$ thẳng hàng tức là $XM,EF$ cắt nhau tại $K$. 

Lấy $I'$ đối xứng với $I$ qua $EF$ thì $I'$ là trực tâm tam giác $AEF$.

Áp dụng định lí về điểm $Anti steiner$ dễ chứng minh được $X$ chính là điểm $Anti steiner$ đối với đường thẳng $HI'$ của tam giác $AEF$ nên $HI',EF$ và $XM$ từ đó nhận thấy $HI',EF$ và $XM$ đồng quy tại $K$. 

Do 2 đường thẳng $HI'$ và $XM$ đối xứng nhau qua $EF$ (theo $Anti steiner$) nên $KD $là phân giác $\angle IKH$

Bài toán được chứng minh.

Cho tam giác $ABC$ có $I$ là tâm nội tiếp. $(I)$ tiếp xúc với $BC,CA,AB$ tại $D,E,F.$ Hạ $DK\perp EF$ và $H$ là trực tâm tam giác $ABC$.

Chứng minh $KD$ là phân giác $\angle IKH$.

Mình sử dụng $Anti steiner$ và vị tự nhưng thấy khá phức tạp! Mọi người ai có ý kiến gì thì đóng góp nhé!

Bài này mình giải ra nhưng mà kết quả lại sai, mình cũng ko biết sai chỗ nào hết. Mong các bạn giúp đỡ!

Đây là lời giải của mình:

Gọi $R$ là giao điểm $HL$ và $BC$. Qua $A$ kẻ đường thằng song song với $BC$ cắt $EF$ và $HL$ tại $Q$ và $U$.

Dễ thẩy $R, E, F, Q$ thằng hàng mà chùm $R(A,H,F,B)=-1$ nên $Q$ là trung điểm $AU$ nên $PQ$ là đường trung trực của $AL$.

$QURP$ là hình bình hành mà $AQ=QU$ nên $AQRP$ là hình bình hành nên $\angle AQF=\angle APC$ nên $\triangle AQF$ đồng dạng $\triangle APC$ mà $\triangle AEF$ đồng dạng $\triangle ABC$ nên $\frac{QE}{EF}=\frac{PB}{BC}$.

Dế chứng minh được $\triangle LEF$ đồng dạng $\triangle LBC$ nên kết hợp điều trên ta có $\Delta LQE$ đồng dạng $\Delta LPB$ suy ra $\Delta LEB$ đồng dạng $\Delta LQP$ nên $LEFQ$ nội tiếp $\Rightarrow \angle LSE=\angle LQE$ nên $\angle LSB=\angle LQR$  

Dễ thấy $LQPR$ là hình thang cân $\Rightarrow \angle LQR=\angle LPR$ vậy $\angle LSB=\angle LPB$ ta có điều phải chứng minh.

P/s: Mình làm hơi tắt, mấy bạn thông cảm

để ý $BE$ và $CF$ đi qua trực tâm H ta có thể tổng quát bài toán trên cho 2 điểm đẳng giác

bỏ các giả thiết $O$ và $H$ là tâm đường tròn ngoại tiếp và trực tâm và thay vào đó là 2 điểm liên hợp đẳng giác bất kì 

gọi $D=BC\cap AI$ 

Do $O$ và $F$ là 2 điểm đẳng giác góc $C$ của tam giác $CKB$ nên dễ thấy $OB, FK, CL$ đồng quy tại $U$

gọi $X=FI\cap BU$

Ta có $L(B,I,X,K)=-1$ và $L(B,I,D,K)=-1$ nên $L,X,D$ thẳng hàng nên $X=LD\cap OB$ và $F,X,I$ thẳng hàng

Tương tự gọi $Y=KD\cap OC$ thì ta có $E,Y,I$ thằng hàng

áp dụng định lí Pappus cho 6 điểm $L,O,K,B,D,C$ ta có $X,I,Y$ thẳng hàng => $F,X,I,Y,E$ thẳng hàng => $E,F,I$ thẳng hàng

điều ngược lại chứng minh tương tự như trên 

ta có đpcm

cho 2 đường tròn $\odot(O)$ và $\odot(O')$ không cắt nhau . gọi $d$ là trục đẳng phương của 2 đường tròn này. 1 đường thẳng bất kì cắt  $\odot(O)$ và $\odot(O')$ lần lượt tại $X,B,Y,C$, $X,B\in (O); Y,C \in (O')$. Gọi $A$ và $T$ là 2 điểm bất kì thuộc $d$. Đường thẳng bất kì qua $T$ cắt $AB,AC$ lần lượt tại $E,F$. Đường thẳng bất kì qua $T$ cắt $AX,AY$ lần lượt tại $G,H$. Gọi $S$ là giao điểm của $GF$ và $HE$. Chứng minh $AS$ song song với $BC$

cách giải của mình k hay. Mọi người góp ý nha 

Bạn có chắc chắn đúng đề không vậy?  Mình vẽ hình thấy đâu có thỏa! 

Post 148.png

xin lỗi bạn, mình vừa sửa lại đề

Mình chỉ mới chứng minh được trong trường hợp $M,N,P$ là trung điểm của $BC,CA,AB$

Mình giải như sau:

Gọi

 $\odot (I)$  là đường tròn nội tiếp $\Delta ABC$

$\odot (I')$ là đường tròn nội tiếp $\Delta MNP$ 

$V$ là tiếp điểm của $\odot (I')$ và $NP$

$Q$ là tiếp điểm của đường tròn bàng tiếp $\angle A$ và $BC$

$D$ là tiếp điểm của $\odot (I)$ và $BC$

$T$ là giao điểm của $AQ$ và $\odot (I)$ thì dễ chứng minh được $MT$ là tiếp tuyến của  $\odot (I)$

Do $\Delta ABC$ đồng dạng $\Delta MNP$ nên:

$\frac{VN}{VP} = \frac{DB}{DC} =\frac{QC}{QB}$ nên $A$, $V$, $Q$ thẳng hàng

suy ra bốn điểm $A,V,T,Q$ thẳng hàng

ta có $\angle XVT = \angle AVP=\angle AQB=\angle MTQ=\angle VTX$ nên $\Delta XVT$ cân tại $X$ => $XV=XT$

 nên $X$ thuộc trục đẳng phương của  $\odot (I)$ và $\odot (I')$

tương tự $Y$ và $Z$ cũng thuộc trục đẳng phương của   $\odot (I)$ và $\odot (I')$

nên $X, Y, Z$ thẳng hàng