$\boxed{\text{Lời giải khác cho bài toán 81}}$.

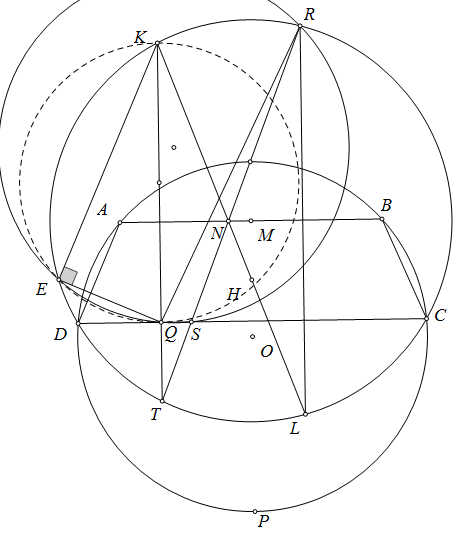
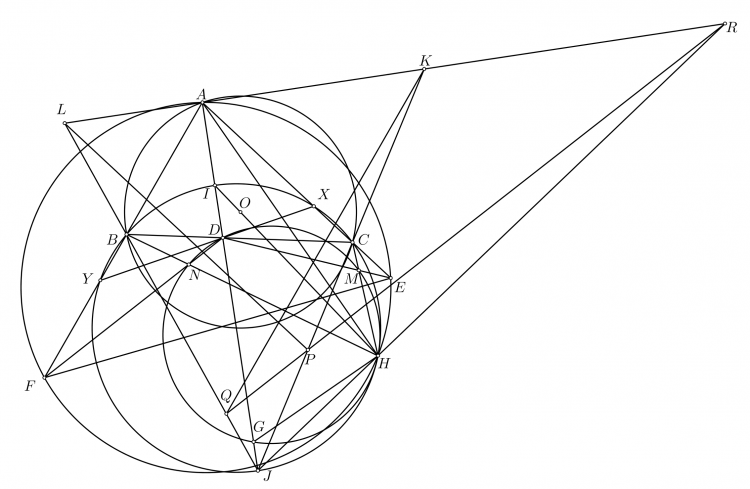
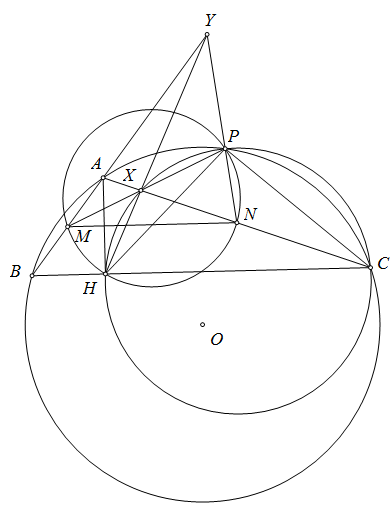
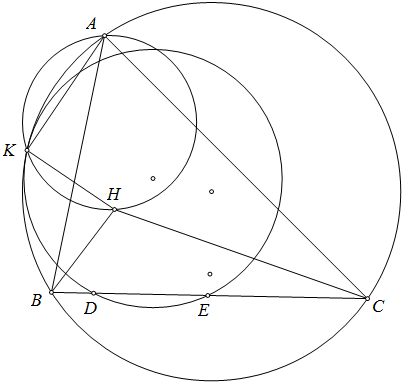
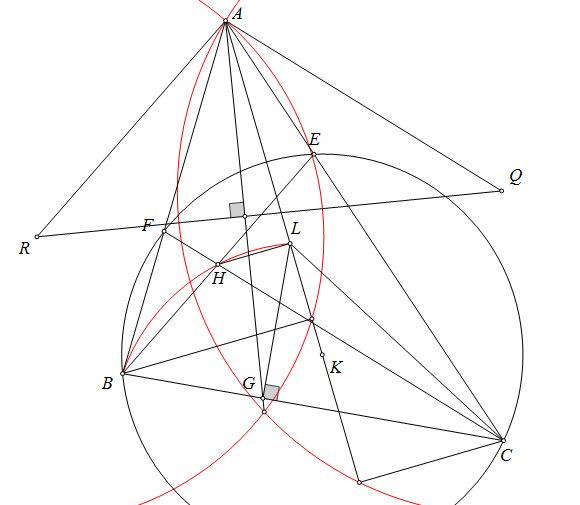
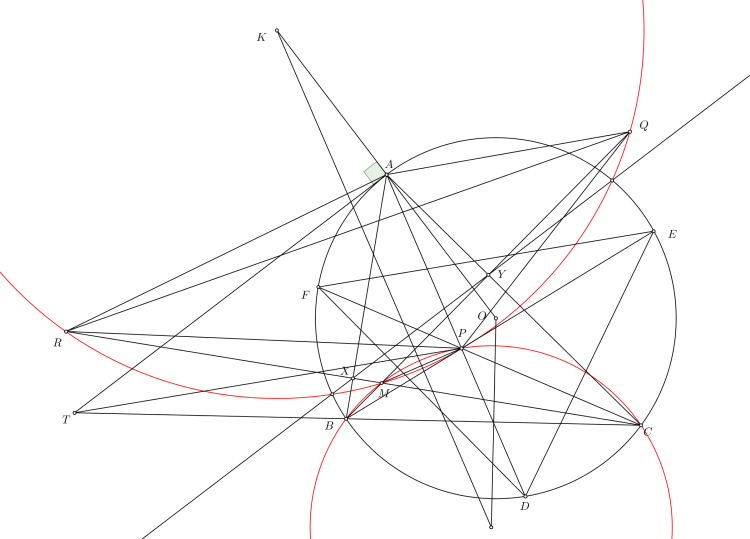
Gọi $O,H,N$ lần lượt là trực tâm, tâm ngoại tiếp và tâm đường tròn $Euler$ của tam giác $IED$. Gọi $O'$ là đối xứng của $O$ qua $DE$ thì $OO'=IH$. Từ đó $IHO'O$ là hình bình hành suy ra $AO'$ đi qua $N$ là trung điểm $OH$. Do đó ta chỉ cần chứng minh $AI$ đi qua $O'$ là đối xứng của $O$ qua $DE$ đồng thời là tâm đường tròn ngoại tiếp tam giác $HED$. Đường thẳng qua $D,E$ lần lượt song song với $CI,BI$ cắt nhau tại $P$ thì tứ giác $PDEH$ nội tiếp. Gọi $(O')$ cắt $AC,AB$ tại $M,N$. Do $\angle AEM=\angle PDM+\angle AEP=\angle B/2+\angle C/2=180^\circ-\angle BIC=180^\circ-\angle EPD=180^\circ-\angle EMD$ nên từ đó $EMND$ là hình thang cân suy ra $AI$ đi qua tâm $(EMND)$ hay $AI$ đi qua $O'.\ \blacksquare$

PS. Anh Dương đề xuất bài toán mới đi ạ!

$\boxed{\text{Lời giải bài toán 82}}$. Bài này khá đơn giản!

Gọi $X,Y,Z$ lần lượt là giao điểm của $(AOX)(BOY)(COZ)$ với $(O)$. Do tứ giác $AOXD$ nội tiếp nên $\angle ADX=180^\circ-\angle AOX=2\angle OAX=2\angle ODX$. Từ đó $DA,DX$ đẳng giác trong $\angle BDC$. Chú ý tam giác $BDC$ đều nên từ đó $AD,AX$ đẳng giác trong $\angle A$. Theo định lí $Napoleon$ thì $AX,BY,CZ$ đồng quy tại điểm đẳng giác với điểm $Napoleon$ của tam giác $ABC$. Gọi điểm đó là $K$.

Gọi $OK$ cắt $(AOX)$ tại $T$ thì $OA^2=OK.OT$ từ đó $T$ xác định duy nhất trên $OK$. Mặt khác do $OA=OB=OC$ nên ba đường tròn $(AOX)(BOY)(COZ)$ đồng quy tại $T.\blacksquare$

PS. Kết quả về ba đường tròn đồng quy dạng này thì khá nhiều và quen thuộc với các chứng minh hoàn toàn tương tự như trên. 

Một kết quả khác như sau. Cho tam giác $ABC$ nội tiếp đường tròn $(O)$. Gọi $X,Y,Z$ lần lượt là đối xứng của $A,B,C$ qua $BC,CA,AB$. Khi đó $(AOX)(BOY)(COZ)$ đồng quy.

Chứng minh hoàn toán tương tự như trên, chú ý điểm cần tìm ở đây là điểm $Konista$ của tam giác $ABC$.

Đề xuất bài toán tiếp theo khá nhẹ nhàng!

$\boxed{\text{Bài toán 83}}$.(AoPS) Cho tam giác $ABC$, trực tâm $H.M$ là trung điểm $BC$. Trên $BC$ lấy $S$ sao cho $HS,HM$ đẳng giác. Hạ $AP\perp HS$. Chứng minh rằng $(MSP)$ tiếp xúc $(ABC)$.

$\boxed{\text{Bài toán 80}}$ đã lâu chưa có lời giải nên mình sẽ đưa ra lời giải để tiếp tục topic.

$\boxed{\text{Lời giải bài toán 80}}$.

Hình 1.

Đầu tiên ta sẽ chứng minh $\angle KEQ=90^\circ$. Biến đổi góc : $\angle REQ=180^\circ-\angle RSQ=\angle RNB=\angle LNB,\ \angle KER=\angle KLR$. Chú ý $RL\perp AB$ nên $\angle KEQ=\angle REQ+\angle KER=90^\circ$. Từ đó $E\equiv (KQ)\cap (M).$

Hình 2.

Do $AB$ đi qua tâm $M$ của $(M)$ nên dễ thấy $RN$ cắt $KQ$ tại $T$. Gọi $S$ là điểm chính giữa cung $AB$ không chứa $CD$ của $\Omega$. Chú ý trực tâm $H$ đối xứng với $S$ qua $AB$ nên $TR$ đi qua $S$. Tiếp theo ta sẽ chứng minh $QS$ đi qua $F$. Gọi $Z,G$ lần lượt là giao điểm của $KF$ và $EQ$ với $(M)$. Chú ý rằng $M$ là trung điểm $HS,HK\perp KZ$ nên $\angle KZS=90^\circ$. Từ đó $ZS$ đi qua $G$. Từ đây theo định lí $Pascal$ thì $F,S,Q$ thẳng hàng.

Gọi $QS$ cắt đường tròn $(KEF)$ tại $X$. Do $\angle KXF=\angle KER=\angle KTR$ từ đó tứ giác $KSTX$ nội tiếp suy ra $QX.QS=QT.QK=QD.QC$ kéo theo tứ giác $SCXB$ nội tiếp. 

Do tứ giác $KHST$ nội tiếp nên năm điểm $K,H,S,T,X$ cùng thuộc một đường tròn. Từ đó $\angle FKX=90^\circ+\angle HKX=90^\circ+\angle HSX=\angle XDS$. Từ đó $(KEF)$ tiếp xúc đường tròn $\Omega. \ \blacksquare$

Việc đề xuất bài toán mới thì thầy có thể giúp đỡ được không ạ?

Nguồn gốc bài toán: http://www.artofprob...1202245p5915727

PS. Thành thật xin lỗi vì việc trùng điểm $S$ nên mình phải vẽ ra hai hình cho tiện!

Đề xuất bài toán mới để tiếp tục topic.

$\boxed{\text{Bài toán 80}}$ (AoPS) Cho hình thang cân $ABCD$ nội tiếp đường tròn $\Omega$ với $AB\parallel CD.M$ là trung điểm $AB$ và $P$ là điểm chính giữa cung $CD$ không chứa $A$ của $\Omega$. Gọi $H$ là trực tâm tam giác $PAB$ và $(M)$ là đường tròn tâm $M$ đi qua $C,D.N$ là một điểm trên đoạn $AB$ ($N$ khác $A,B$ và $M$). Đường thẳng $HN$ cắt $(M)$ tại $K,L$ sao cho $L$ nằm trong $\Omega$. Chọn hai điểm $Q,R$ theo thứ tự thuộc $CD$ và $(M)$ sao cho $KQ,LR$ cùng vuông góc với $AB$. Gọi $RN$ cắt $CD$ tại $S$. Đường tròn ngoại tiếp tam giác $QRS$ cắt lại $(M)$ tại $E$. Chọn $F$ trên $ER$ sao cho $KF\perp KL$. Chứng minh rằng đường tròn ngoại tiếp tam giác $KEF$ tiếp xúc $\Omega$

Tiếp nối lời giải $\boxed{\text{bài 78}}$. (Ta thay điểm $K$ bởi $G$ vì bị trùng lặp)

$\textbf{Lời giải.}$ Gọi $J$ là tâm đường tròn bàng tiếp $\angle A$.Theo lời giải trên dễ thấy $R,H,J$ thẳng hàng do đó $H$ thuộc đường tròn đường kính $IJ$. Do $(AFIJ)=-1$ nên $HI$ là phân giác $\angle AHD$ suy ra $\angle IDH=\angle AHI=\angle JHG$ do đó $HD,HG$ đẳng giác trong $\angle IHJ$.Vậy đường tròn $(DHG)$ tiếp xúc $(JBC)$.

 Gọi $X,Y$ lần lượt là giao điểm của đường tròn đường kính $IJ$ với $CA,AB$. Dễ thấy $X,D,Y$ thẳng hàng. Do đường tròn $(HMN)$ tiếp xúc đường tròn $(HBC)$ nên $MN\parallel BC$. Do đó $\angle EDH=\angle MNH=\angle CBH=\angle HXC$ suy ra tứ giác $DXEH$ nội tiếp. Tương tự thì tứ giác $DYFH$ nội tiếp. Ta suy ra $\angle EHF=\angle EHD+\angle FHD=\angle DXA+\angle DYA=180^\circ-\angle BAC$ do đó tứ giác $AEHF$ nội tiếp. $\square$

Đề nghị bài toán mới.

$\boxed{\text{Bài toán 79}}$ (AoPS) Cho tam giác $ABC$ nội tiếp đường tròn $(O)$ và $H$ là hình chiếu của $A$ lên $BC.P$ là một điểm trong tam giác sao cho $\angle PBA=\angle PCA.Q$ là một điểm trên $(O)$ sao cho $\angle AQP=90^\circ$. Phân giác trong các góc $\angle QBP,\angle QCP$ cắt nhau tại $D$. Các điểm $K,L$ lần lượt trên $AB,AC$ sao cho $HK\perp BD,HL\perp CD$. Các điểm $M,N$ trên $CA,AB$ sao cho $KM\parallel BP,LN\parallel CP$.Chứng minh rằng $(AMN)$ tiếp xúc $(BCD)$

$\boxed{\text{Lời giải bài toán 89.}}$ Gọi $A_6$ là giao điểm của $AA_0$ với $(N).A_3'$ là giao điểm của $AA_1$ với $(N)$.

Ta có $\angle AA_6A_3'=\angle AA_1A_0=A_3'AA_2$ nên $AA_2$ tiếp xúc đường tròn $(AA_3'A_6)$.

Mặt khác $\angle AC_0B_0=\angle ACB=\angle CAA_2$ nên $AA_2$ tiếp xúc đường tròn $(AB_0C_0)$.

Từ đó các đường tròn $(AA_3'A_6)$ và $(AB_0C_0)$ tiếp xúc nhau. Theo định lí về tâm đẳng phương ta suy ra $B_0C_0,AA_2,A_3'A_6$ đồng quy.

Do đó $A_3'A_6$ đi qua $A_2$. Từ đó $A_2A_3'A=90^\circ$ nên $A_3\equiv A_3'$.

Do $A_4$ và $N$ lần lượt là tâm đường tròn $\text{Euler}$ của tam giác $ABC$ và đường tròn đường kính $AA_2$, để ý rằng $A_3$ là giao của hai đường tròn này nên $A_5$ đối xứng với $A_3$ qua đoạn nối tâm sẽ là giao điểm thứ hai của hai đường tròn. Từ đó $\angle AA_5A_2=90^\circ$. 

Gọi $A_2A_0$ cắt $(N)$ tại điểm $A_5'$ khác $A_0$. Ta có $\mathcal{P}_{A_2/(N)}=A_2A^2=A_2A_5'.A_2A_0$ nên $\angle AA_5'A_2=90^\circ$.

Do đó $A_5\equiv A_5'$.

Gọi $X$ là giao điểm của $A_5$ với $(N)$. Do $\angle AA_5A_0=90^\circ$ nên $X$ đối xứng với $A_0$ qua $N$, từ đó $X$ thuộc trung trực $BC$.

Từ đây áp dụng định lý $\text{Ceva}$ dạng lượng giác cho các tam giác $AB_1C_1,BC_1A_1,CA_1B_1$. Chú ý rằng 

\[\frac{\sin \angle XB_1C_1}{\sin \angle ZB_1A_1}.\frac{\sin \angle ZA_1B_1}{\sin \angle YA_1C_1}.\frac{\sin \angle YC_1A_1}{\sin \angle XC_1B_1}=1\]

và các cặp góc bằng nhau $\angle XB_1A_1=\angle YA_1B_1,\angle XC_1B_1=\angle ZA_1B_1,\angle YC_1A_1=\angle ZB_1A_1$ ta suy ra

\[\prod \frac{\sin \angle XAB_1}{\sin \angle XAC_1}=1\]

Từ đó theo định lý $\text{Ceva}$ dạng lượng giác ta suy ra $AX,BY,CZ$ đồng quy hay $AA_5,BB_5,CC_5$ đồng quy. $\blacksquare$

Đề xuất bài toán mới để tiếp tục topic!

$\boxed{\text{Bài toán 90}}$ (Đặc biệt hóa) Cho tam giác $ABC$, trọng tâm $G$, điểm $\text{Lemoine}$ $L$. $U,V$ lần lượt là hình chiếu của $L,G$ trên $BC$. Gọi $J$ là giao điểm khác $A$ của đường tròn $(AUV)$ và đường tròn $(ABC)$. $AT$ là đường kính của đường tròn $(ABC)$. Chứng minh rằng $JT$ chia $LU,GV$ cùng tỉ số.

Tác giả bài toán tổng quát là "đại ca" Trần Quang Huy!

Bài toán $90$ đúng trong trường hợp tổng quát hai điểm liên hợp đẳng giác, bài này đã được anh Huy đưa lên AoPS tại đây và có lời giải của Telv Cohl.

Đề xuất bài toán tiếp theo khá nhẹ nhàng để tiếp tục topic.

$\boxed{\text{Bài toán 91}}$ (Own) Cho hai đường tròn $(O)$ và $(O_1)$ cắt nhau tại $B,C;M$ là trung điểm $BC$. Điểm $A$ chạy trên $(O)$ và khác $B,C.AB,CA$ theo thứ tự cắt $(O_1)$ tại $F,E;P,Q$ lần lượt là hình chiếu của $A$ lên $BE,CF$. Dựng hình bình hành $MPKQ$. Chứng minh rằng $AK$ luôn đi qua một điểm cố định.

Link lời giải bài toán 141 :  http://artofproblems...1341458p7284966

Lời giải bài toán 138. Dễ thấy $M,I,N$ thẳng hàng, ta có $\angle PMA=180^\circ-\angle AIB=\frac{1}{2}\cdot (\angle A+\angle B)=90^\circ-\frac{1}{2}\cdot \angle C=90^\circ-\frac{1}{2}\cdot \angle MPA$ nên $\triangle MPA$ cân suy ra $\overline{PA}=\overline{PM}$. Tương tự thì $\overline{PA}=\overline{PN}$ nên $P$ là tâm đường tròn ngoại tiếp tam giác $AMN$.Gọi $E,F$ lần lượt là giao điểm của $AP$ với các đường tròn $(AIB)$ và $(AIC)$. Do $\measuredangle AEM=\measuredangle ABM=\measuredangle ACP$ nên $ME\perp OP$. Tương tự thì $NF\perp OP$ do đó $ME\parallel NF$. Gọi $S,T$ lần lượt là giao điểm của $PB,PC$ với đường thẳng qua $A$ vuông góc với $PO$. Do $ST\parallel ME\parallel NF$ nên theo định lí Thales \[\frac{\overline{SM}}{\overline{SP}}=\frac{\overline{AE}}{\overline{AP}},\frac{\overline{TP}}{\overline{TN}}=\frac{\overline{AP}}{\overline{AF}}\Rightarrow \frac{\overline{SM}}{\overline{SP}}\cdot \frac{\overline{TP}}{\overline{TN}}=\frac{\overline{AE}}{\overline{AF}}\] Mặt khác do các tam giác $APM$ và $APN$ cân tại $P$ nên $BE\parallel AM, CF\parallel AN$ suy ra $\overline{AE}=\overline{MB}, \overline{AF}=\overline{NC}$. Do đó $\overline{AE}:\overline{AF}=\overline{MB}:\overline{NC}$. Gọi $X$ là giao điểm của $MN$ với $ST$. Áp dụng định lí Menelaus cho tam giác $SPT$, cát tuyến $M,N,X$ ta suy ra \[\frac{\overline{SM}}{\overline{SP}}\cdot \frac{\overline{TP}}{\overline{TN}}\cdot \frac{\overline{XN}}{\overline{XM}}=1\Rightarrow \frac{\overline{AE}}{\overline{AF}}=\frac{\overline{XM}}{\overline{XN}}\Rightarrow \frac{\overline{MB}}{\overline{NC}}=\frac{\overline{XM}}{\overline{XN}}\] Gọi $K,L$ lần lượt là giao điểm của $MQ,NR$ với đường thẳng $ST$. Theo định lí Thales \[\frac{\overline{KM}}{\overline{LN}}=\frac{\overline{XM}}{\overline{XN}}\Rightarrow\frac{\overline{KM}}{\overline{LN}}=\frac{\overline{MB}}{\overline{NC}}\] Mặt khác do $\overline{PM}=\overline{PN}$ nên $\triangle MPN$ cân tại $P$ nên $\measuredangle MNP=\measuredangle NMP$ suy ra $\measuredangle KMB=\measuredangle LNC$. Từ đó $\triangle KMB\sim \triangle LNC$ (cạnh - góc - cạnh) suy ra $\measuredangle KBM=\measuredangle LCN$. Do đó $\angle AKB=\angle KSB+\angle KBS=90^\circ-\angle OPB+\angle LCN=\angle BCP+\angle LCN=180^\circ-\angle BCL$ suy ra tứ giác $KBCL$ nội tiếp.\\ Gọi $Z$ là giao điểm của $ST$ với $BC$, theo tính chất phương tích $\overline{ZK}\cdot \overline{ZL}=\overline{ZB}\cdot \overline{ZC}$. Mặt khác do $\angle MKA=180^\circ-\measuredangle (PO,MN)=180^\circ-(\angle BMI+\angle BPO)=180^\circ-(\frac{1}{2}\cdot\angle A+\angle BPO)=90^\circ+\angle BAP$ $-\frac{1}{2}\cdot \angle A=90^\circ+\frac{1}{2}\angle A-\angle PBC=180^\circ-(90^\circ-\frac{1}{2}\angle A)-\angle MBQ=\angle BQM$ nên tứ giác $KLRQ$ nội tiếp suy ra $\overline{ZK}\cdot \overline{ZL}=\overline{ZQ}\cdot \overline{ZR}$. Do đó $\overline{ZB}\cdot \overline{ZC}=\overline{ZQ}\cdot \overline{ZR}$ nên $Z$ thuộc trục đẳng phương của các đường tròn $(O)$ và $(AQR)$ suy ra $AZ$ là trục đẳng phương của $(O)$ và $(AQR)$, từ đó suy ra tâm đường tròn ngoại tiếp tam giác $AQR$ thuộc $OP$ do $OP\perp AZ$. $\square$

Lời giải bài toán 126. Ta phát biểu bài toán về dạng dễ nhìn hơn như sau :

Bài toán 126'. Cho tam giác $ABC$ nội tiếp đường tròn $(O)$, trực tâm $H$. $P$ thuộc $OH$. Gọi $X$, $Y$, $Z$ lần lượt là đối xứng của $P$ qua trung trực $BC$, $CA$, $AB$. Chứng minh rằng $AX$, $BY$, $CZ$ đồng quy.

Giải. Bổ đề (Định lý Steiner). Cho tam giác $ABC$. $D$, $E$ là hai điểm bất kỳ trên $BC$. Khi đó $AD$, $AE$ đẳng giác trong $\widehat{BAC}$ khi và chỉ khi $\tfrac{DB}{DC}\cdot \tfrac{EB}{EC}=\tfrac{AB^2}{AC^2}$

Quay lại bài toán. Ta sẽ chứng minh $AX$, $BY$, $CZ$ đồng quy tại một điểm có điểm liên hợp đẳng giác thuộc $OH$.

Gọi $T$ là giao điểm của $AX$ với $OH$, đường đẳng giác với $AX$ trong $\widehat{BAC}$ cắt $OH$ tại $S$.

Do $AO$, $AH$ đẳng giác nên $AX$, $AS$ đẳng giác trong $\widehat{OAH}$.

Theo định lý Steiner ta suy ra, 

\[\frac{SH}{SO}=\frac{AH^2}{AO^2}\cdot \frac{TO}{TH}\Rightarrow \frac{SH}{SO}=\frac{AH^2}{AO^2}\cdot \frac{TO}{TH}\]

Gọi $G$ là giao điểm của $XO$ với $AH$, $R$ là giao điểm của đường tròn $(ARO)$ với $AO$.

Áp dụng định lý Menelaus cho tam giác $OGH$ với $\overline{ATX}$ ta thu được,

\[\frac{TO}{TH}=\frac{XO}{XG}\cdot \frac{AG}{AH}\Rightarrow \frac{SH}{SO}=\frac{AH\cdot XO\cdot AG}{AO^2\cdot XG}\]

Do $\tfrac{XO}{XG}=\tfrac{OP}{OP+OH}$ nên,

\[\frac{SH}{SO}=\frac{AH\cdot OP\cdot AG}{AO^2\cdot (OP+OH)}\]

Do tứ giác $HGRO$ nội tiếp nên $AG\cdot AH=AR\cdot AO$.

Chú ý các góc $\widehat{HRO}$ và $\widehat{AHO}$ bằng nhau nên $\triangle HRO\sim \triangle AHO$.

$\Rightarrow OR=\tfrac{OH^2}{AO}$

Từ đó,

\[\frac{SH}{SO}=(1-\frac{OH^2}{OA^2})\cdot \frac{OP}{OP+OH}\]

Tương tự với $B$, $C$, ta suy ra $AX$, $BY$, $CZ$ đồng quy tại điểm liên hợp đẳng giác với $S$ đối với tam giác $ABC$. $\square$

Lời giải bài toán 93 đã có ở đây http://artofproblems...endicular_to_bc

Theo yêu cầu của bạn Nguyen Dinh Hoang, xin đề xuất bài toán mới. 

$\boxed{\text{Bài toán 67}}$ (Trần Quang Hùng ~ Nguyễn Đức Bảo) Cho tam giác $ABC$. Một đường tròn $(K)$ qua $B,C$ cắt $CA,AB$ tại $E,F.H$ là giao điểm của $BE,CF$. Kẻ $HL\perp AK,LD\perp BC.M$ là trung điểm $BC.AK$ cắt $(CL)$ tại $N$. Đường thẳng qua $A$ song song với $CH$ cắt trung trực $AN$ tại $Q$

Chứng minh rằng $(Q,QA),(CL),(MD)$ đồng quy.

Mô hình bài toán này khá giống với một bài toán mình đề nghị trong topic, tất cả đều dựa trên mô hình bài toán ??? của thầy Trần Quang Hùng!

Nguồn gốc bài 66: http://www.artofprob...1108467p5035848

Lời giải bài toán 65 có thể tham khảo thêm lời giải khác của anh Huy tại đây.

Theo đề nghị của anh Khánh, đề xuất bài toán tiếp theo.

$\boxed{\text{Bài toán 66}}$ (AoPS) Cho hai đường tròn $(O),(O')$ có tâm vị tự ngoài $V.l$ là đường thẳng qua $V$ vuông góc với $OO'$. Hai điểm $P,Q$ trên $(O),(O')$ sao cho $V,P,Q$ thẳng hàng. Tiếp tuyến tại $P$ của $(O)$ cắt tiếp tuyến tại $Q$ của $(O')$ tại $X.XP,XQ$ cắt $l$ theo thứ tự tại $Y,Z$. Chứng minh rằng khi $P,Q$ thay đổi thì đường tròn ngoại tiếp tam giác $XYZ$ tiếp xúc với một đường tròn cố định.

Một cách khác cho bài 29, dài hơn một chút!

$\boxed{\text{Lời giải bài toán 29}}$ (Cách này có lẽ phù hợp với mấy đứa chưa học biến hình như em)

$\boxed{\text{Bổ đề 1}}$ Cho tam giác $ABC,L$ là điểm Miquel. $M$ là trung điểm $BC.$ Đường cao $AH$. Khi đó $ML$ chia đôi $AH$.

Bổ đề trên là bổ đề quen thuộc về điểm Lemoine, mình học từ anh viet nam in my heart, về chứng minh mọi người có thể nhắn tin qua anh viet nam in my heart hoặc đọc trong các tài liệu về điểm Lemoine.

Giải bài toán. (Có lẽ vẫn cần tính toán nhưng không dài như anh Ngockhanh99k48)

Dễ thấy chỉ cần chứng minh $AA'$ đi qua trung điểm $OL$.

$T\equiv AD\cap OA'$. Theo tính chất quen thuộc, dễ thấy $(AD,LT)=-1.N,P$ theo thứ tự là trung điểm $AH,AD$. Do $AFDE$ là hình bình hành nên $P$ là trung điểm $EF\Longrightarrow A'P\perp EF\Longrightarrow AO\parallel A'P$. Áp dụng bổ đề 1 ta suy ra $M,L,N$ thẳng hàng. Mặt khác do $(AD,LT)=-1$ nên theo định lí Thales ta suy ra $A'D\parallel OL$. Mặt khác $A'(DA,LO)=-1\Longrightarrow AA'$ đi qua trung điểm $OL.\blacksquare$

Bài này không cần tính điểm đâu nhé! Anh viet nam in my heart đề xuất bài mới đi!

$\boxed{\text{Lời giải bài toán 33}}$. Theo lời giải $\boxed{\text{Bài toán 1}}$ của anh Ngockhanhk9948 thì $\angle OMA=40^\circ$.

Mặt khác $\angle AMB=180^\circ-80^\circ-30^\circ=70^\circ\Longrightarrow \angle OMC=70^\circ\Longrightarrow \angle OKF=20^\circ$.

Lại có $\angle AOM=180^\circ-\angle MAO-\angle OMA=180^\circ-20^\circ-40^\circ=120^\circ$. Mà theo lời giải $\boxed{\text{Bài toán 1}}$ của anh dogsteven thì $\angle AOI=60^\circ\Longrightarrow \angle KOI=60^\circ$ hay $\triangle OIK$ đều.

Đường thẳng qua $K$ vuông góc với $OI$ cắt $OF$ tại $T$. Dễ thấy $\angle FKT=\angle 30^\circ-20^\circ=10^\circ\Longrightarrow \triangle TFK$ cân tại $F$ hay $T$ thuộc $(F,FK)$. Mặt khác theo lời giải $\boxed{\text{Bài toán 1}}$ của anh I Hate Math thì $\angle OSK=20^\circ$ với $S$ là điểm chính giữa cung $BC$ không chứa $A$ nên $T$ thuộc $(O)$. Mặt khác $T,F,O$ thẳng hàng nên $(F,FK)$ tiếp xúc $(O).\blacksquare$.

P/s.

Sao không ai giải cả vậy! Mọi người cùng quẩy cho topic sôi nổi đi chứ

Bài toán đề nghị. $\boxed{\text{Bài toán 34}}$. (AopS). Cho hình thang cân $ABCD$ nội tiếp $(O).DO$ cắt $BC$ tại $X$. Đường thẳng qua $X$ song song với $OA$ cắt $AB,AC$ theo thứ tự tại $E,F.(O')\equiv (DEF)$. Tiếp tuyến tại $A$ của $(O)$ cắt $(O')$ tại $P,Q$. Chứng minh rằng $(O'PQ)$ tiếp xúc $(O)$.

$\textbf{Hình vẽ bài toán}$

$$\begin{array}{| l | l |} \hline Ngockhanh99k48 & 6\\ \hline IHateMath & 1\\ \hline fatcat12345 & 5\\ \hline dogsteven & 5\\ \hline baopbc & 8\\ \hline QuangDuong12011998 & 3\\ \hline xuantrandong & 2\\ \hline mrjackass & 1\\ \hline vietnaminmyheart & 3\\ \hline BuiBaAnh & 1\\ \hline halloffame & 2\\ \hline\end{array}$$

$\boxed{\text{Lời giải bài toán 26}}$. Ta có $\angle HPM=\angle MNH=\angle MNA=\angle ACB\Longrightarrow P,X,H,C$ cùng thuộc một đường tròn 

$\Longrightarrow \angle PHX=\angle PCA$. Tương tự thì $\angle PHY=\angle PBA\Longrightarrow \angle PHX=\angle PHY\Longrightarrow H,X,Y$ thẳng hàng hay $XY$ đi qua $H.\blacksquare$

Hình vẽ bài toán

Bài toán đề nghị. $\boxed{\text{Bài toán 27}}$ (AopS) Cho tam giác $ABC,H$ là một điểm sao cho $\angle HBA=\angle HCA$. Trên đoạn $B,C$ lấy các điểm $D,E$ sao cho $\angle DHB=\angle EHC$. Trên $(ABC)$ lấy $K$ sao cho $\angle AKH=90^\circ$. Chứng minh rằng đường tròn ngoại tiếp tam giác $KDE$ tiếp xúc $(ABC)$.

Hình vẽ bài toán

$$\begin{array}{| l | l |} \hline Ngockhanh99k48 & 3\\ \hline IHateMath & 1\\ \hline fatcat12345 & 3\\ \hline dogsteven & 4\\ \hline baopbc & 7\\ \hline QuangDuong12011998 & 2\\ \hline xuantrandong & 2\\ \hline mrjackass & 1\\ \hline vietnaminmyheart & 2\\ \hline BuiBaAnh & 1\\ \hline halloffame & 1\\ \hline\end{array}$$

$\boxed{\text{Lời giải bài 15}}$ Bài này dùng biến đổi góc là được!

Gọi $S$ là giao của $\odot (ABC)$ với $\odot (W_2)$.

Ta có: $\measuredangle XYS=180^\circ-\measuredangle YCS=\measuredangle AQS=\measuredangle ABS\Longrightarrow X,Y,S,B$ đồng viên.

$\measuredangle XQS=\measuredangle AQS-\measuredangle AQX=\measuredangle XYS-\measuredangle AYX=180^\circ-\measuredangle YKS-\measuredangle AYX=180^\circ-\measuredangle YKS-\measuredangle YKX=180^\circ-\measuredangle XKS$

$\Longrightarrow Q,X,K,S$ đồng viên.

Giả sử $SY$ cắt $AB$ tại $T. \measuredangle TXK=180^\circ-\measuredangle BXK=180^\circ-\measuredangle BPK=180^\circ-\measuredangle TSK$

$\Longrightarrow T,X,K,S$ đồng viên $\Longrightarrow T,Q,K,X$ đồng viên $\Longrightarrow \measuredangle AXQ=\measuredangle TXQ$.

Mặt khác do $X,Y,S,B$ đồng viên nên $\overline{P,K,T}\Longrightarrow \measuredangle AXQ=\measuredangle QKP.\blacksquare$

Bài toán đề nghị.

$\boxed{\text{Bài toán 16}}$. Cho tam giác $ABC.\odot (K)$ bất kì qua $B,C$ cắt $CA,AB$ lần lượt tại $E,F.BE,CF$ cắt nhau tại $H$. Kẻ $HL,BM,CN$ vuông góc với $AK(M,N,P$ thuộc $AK$). Gọi $G$ là hình chiếu của $L$ lên $BC$. Đường thẳng qua $A$ lần lượt song song với $BE,CF$ lần lượt cắt trung trực $AM,AN$ tại $Q,R$. Chứng minh rằng trục đẳng phương của $\odot (Q;QA),\odot (R;RA)$ đi qua $G$.

Nguồn.

$\boxed{\text{Bài toán 1}}$ Cho tam giác $ABC$ có $\angle A=60^\circ,\angle B=80^\circ$ nội tiếp $\odot (O)$, ngoại tiếp $\odot (I)$.

$AI$ cắt $OB$ tại $X$, cắt $BC$ tại $M$. Đường thẳng qua $C$ vuông góc với $AB$ cắt $OM$ tại $K$ và trung trực $BC$ tại $E.ME$ cắt $AC$ tại $L$. Đường thẳng qua $K$ vuông góc với $BC$ cắt $AC$ tại $F$. Chứng minh rằng $E,K,X,I,F,L$ cùng thuộc một đường tròn tâm $O$.

Nguồn.

Hình vẽ bài toán

Ủng hộ câu a, trước. Câu b, chắc để sau vậy!

$\boxed{\text{Lời giải bài toán 43a}}$ Ta sẽ sử dụng bổ đề $Ceva$ trong đường tròn.

Cho tam giác $ABC$ nội tiếp $(O)$, các điểm $A',B',C'$ nằm trên $(O)$. Khi đó $AA',BB',CC'$ đồng quy $\Longleftrightarrow \frac{A'B}{A'C}.\frac{B'C}{B'A}.\frac{C'A}{C'B}=1$

Quay lại bài toán: Biến đổi tỉ số đơn giản $\frac{\sin \angle P_aAE}{\sin \angle P_aAF}=\frac{P_aE^2}{P_aF^2}$

Tương tự và áp dụng bổ đề trên ta suy ra $\frac{\sin \angle P_aAE}{\sin \angle P_aAF}.\frac{\sin \angle P_bBF}{\sin \angle P_bBD}.\frac{\sin \angle P_cCD}{\sin \angle P_cCE}=1$

Theo định lí $Ceva$ dạng lượng giác suy ra $AP_a,BP_b,CP_c$ đồng quy. $\blacksquare$

PS. Anh Khánh ghi nguồn đầy đủ đi chứ?

$\boxed{\text{Lời giải bài toán 44}}$ Bài gốc hay bài tổng quát đều không khó, lời giải của em dựa trên lời giải bài gốc mà em đưa lên trong link!

Do $P$ thuộc trung trực $BC$ nên $\angle QCA=\angle QBA\implies AE=AB,AF=AC\implies \triangle ABF=\triangle AEC$

$\implies BF=CE$. Mặt khác dễ thấy $\angle ECD=\angle DBF$ nên $\triangle DCE=\triangle DBF\implies DE=DF,\angle EDF=\angle BDC$

$\implies \angle EFD=\angle CBD.S\equiv DB\cap (DEF)$. Do $\angle BSE=\angle DFE=\angle DBC$ nên $BC\parallel SE$

Mặt khác dễ thấy $\angle BAE=2\angle DBC=2\angle BSE$ nên $A$ là tâm ngoại tiếp tam giác $BES\implies AK\perp SE\implies AK\perp BC.\blacksquare$

$\boxed{\text{Lời giải bài toán 64}}$

Theo kết quả ELMO (#13) ta suy ra $AK\perp EF.X\equiv AK\cap EF$.

$PL\parallel AO$ khi và chỉ khi $AP$ là phân giác $\angle OAX$ hay $AP$ là phân giác $\angle EAF$

Mặt khác theo kết quả IMO 2010 (Problem 4) ta có điều phải chứng minh.$\blacksquare$

Đề nghị bài toán mới.

$\boxed{\text{Bài toán 65}}$ (AoPS) Cho tam giác $ABC$ với $\angle A\neq 90^\circ$ nội tiếp đường tròn $(O).D$ bất kì trên $BC$. Trung trực $AD$ cắt $OA$ tại $T.TD$ cắt $OB,OC$ tại $E,F$. Kí hiệu $\omega$ là đường tròn qua $A,D$ lần lượt tiếp xúc với $TA,TD$. Chứng minh rằng đường tròn $(OEF)$ tiếp xúc $\omega$

Trâu bò vậy!

$\boxed{\text{Lời giải bài toán 57}}$

Áp dụng công thức đường trung tuyến ta chỉ cần chứng minh:

$MQ^2+NQ^2=MR^2+NR^2 \ (1)$

Theo bổ đề $Carnot$ thì $(1)\iff $

$\cos \angle QRM.MR=\cos \angle NQB.NQ$

$\iff \cos \angle ACD.MR=\cos \angle ABD.NQ$

$\iff sin \angle DAC.MR=\sin \angle ADB.NQ$

$P\equiv AC\cap BD$. Theo định lí $Sin$ thì

$\frac{\sin \angle DAP}{\sin \angle ADP}=\frac{PD}{PA}$

Ta cần chỉ ra

$\frac{NQ}{MR}=\frac{PD}{PA} \ (*)$

Tiếp tục sử dụng định lí $Sin$ và công thức diện tích ta suy ra

$\frac{MR}{MD}=\frac{\sin \angle MCB}{\sin \angle MCD}=\frac{PB.BC}{PD.CD}$

Tương tự thì 

$\frac{NQ}{NA}=\frac{PA.AB}{PC.BC}$

Mặt khác $MD=\frac{1}{2}AC \ , \ NA=\frac{1}{2}BD$ nên dễ suy ra $(*)$ đúng hay đẳng thức được chứng minh $\implies NQ=NR.\blacksquare$

Bài toán đề nghị. $\boxed{\text{Bài toán 58}}$ Cho tam giác $ABC$ nội tiếp $(O).I$ bất kì trên phân giác $\angle A.D,E,F$ lần lượt là hình chiếu của $I$ lên $BC,CA,AB.OI$ cắt $BC$ tại $K.L$ thuộc $AK$ sao cho $AI\parallel DL.LD$ cắt $EF$ tại $X$. Chứng minh rằng $X$ là trung điểm $DL$

Kết quả này mình từng mở rộng từ một bài tập của thầy mình, nếu có trùng lặp mong mọi người thông cảm! Bài toán gốc là khi $I\equiv $ tâm nội tiếp của tam giác $ABC$.

Nhân đề xuất bài toán mới, mình/em xin đưa ra một lời giải khác cho bài toán 54.

$\boxed{\text{Lời giải bài toán 54}}$ 

$E\equiv BQ\cap AC,F\equiv CQ\cap AB,X\equiv BH\cap AC,Y\equiv CH\cap AC$. 

Dễ thấy $QH$ là trục đẳng phương của $(BE)(CF)$. Gọi $M,N$ theo thứ tự là hình chiếu của $E,F$ lên $BA,AC$.

Dễ thấy $P\equiv XM\cap YN$. Mặt khác $M,N,X,Y$ đồng viên nên $PM.PX=PN.PY$ do đó $P$ thuộc trục đẳng phương của $(BE)(CF)$ hay $P,H,Q$ thẳng hàng.

$\boxed{\text{Bài toán 56}}$ (Thầy Trần Quang Hùng) Cho tam giác $ABC$ ngoại tiếp đường tròn tâm $I.(I)$ tiếp xúc $BC$ tại $D$. Trung trực $AD$ cắt $ID$ tại $M$. Gọi $E,F$ theo thứ tự là trung điểm $AD,AI$. Chứng minh rằng $OM$ chia đôi $EF$ với $(O)\equiv (ABC)$.

$\boxed{\text{Lời giải bài toán 55}}$ (Tóm tắt)

$M\equiv CR\cap BQ$. Đế ý $\triangle CAR\sim \triangle EOD,\triangle BAQ\sim \triangle FOD$ dễ suy ra $\angle BMY=\angle BPC\implies B,M,P,C$ đồng viên.

Theo kết quả quen thuộc thì $DE=DF$ từ đó $\triangle CAR\sim \triangle BAQ$

Đế ý $\frac{PB}{PC}=\frac{AB}{AC}\implies \frac{PB}{BQ}=\frac{PC}{PR}\implies \triangle RPC\sim \triangle QPB$

$\implies R,Q,P,M$ đồng viên.

$X\equiv CM\cap AB,Y\equiv BM\cap AC$. Đế ý $\angle ACR=\angle ABQ$ nên $B,X,Y,C$ đồng viên $\implies XY\perp AO$

Đế ý $\angle ABM=\angle ACR=\angle ARC\implies A,R,B,M$ đồng viên $\implies XR.XM=XB.XA\implies X$ thuộc trục đẳng phương của $(O)$ và $(PQR)$.

Tương tự kéo theo $XY$ là trục đẳng phương của $(O)$ và $(PQR)\implies XY\perp OK\implies A,O,K$ thẳng hàng.$\blacksquare$

Chào các thành viên của VMF!

Thay cho lời mở đầu mọi người hãy đọc qua topic sau.

Marathon Số học đã được anh Ego bắt đầu, vì vậy mình xin bắt đầu cuộc thi Marathon Hình học!

Các quy định đã được đề cập rõ tại đây.

Để tăng tính thẩm mĩ mọi người có thể làm theo code sau: